彈性地基上Euler-Bernoulli梁的臨界荷載計算

盧港偉，葛仁余，夏 雨，馬國強，劉小雙，余本源

(安徽工程大學(xué) 建筑工程學(xué)院，安徽 蕪湖 241000)

有關(guān)非均勻和軸向功能梯度(FG)梁的屈曲問題已在文獻中進行了論述，然而，精確的解析解只存在于荷載和抗彎剛度分布的某些特殊情況，在一般彎曲剛度分布的情況下獲得梁的正確解，應(yīng)采用更多的數(shù)值方法。目前，國內(nèi)外計算梁的屈曲臨界荷載的文獻較多，Eisenberger給出了不同剛度和荷載分布的非均勻梁、柱的屈曲實例，研究關(guān)于級數(shù)展開的高精度結(jié)果經(jīng)常用于不同數(shù)值方法的比較和討論。集中荷載作用下非均勻和軸向FG梁屈曲問題的數(shù)值解在許多論文中得到了廣泛研究，Sapountzakis等發(fā)展了用于任意變截面組合Euler-Bernoulli梁彈性屈曲分析的邊界元方法。Coskun等將變分迭代法應(yīng)用于變截面歐拉梁臨界屈曲荷載的確定問題。文獻[9]將邊界條件轉(zhuǎn)換為一種簡便的形式，避免了剛度系數(shù)矩陣的無窮大值問題，研究了軸向功能梯度變截面彈性地基梁的穩(wěn)定性問題。文獻[10]采用局部微分求積法研究了帶有彈性約束的軸向功能梯度變截面樁穩(wěn)定性問題。文獻[11]采用一種低維數(shù)學(xué)模型，該模型能夠計算均勻和非均勻的功能梯度樁沿軸線方向上的屈曲載荷。文獻[12]利用優(yōu)化的瑞利商和Timoshenko商解決了一些工程振動和屈曲穩(wěn)定性問題。文獻[13]給出了各種邊界條件下，變軸力加載的變截面樁屈曲臨界荷載的精確解。文獻[14]提出了一種精確計算任意軸向不均勻梁的臨界屈曲載荷的新方法，將變系數(shù)控制方程轉(zhuǎn)化為線性代數(shù)方程，獲得臨界屈曲載荷。文獻[15-16]采用微分求積法(DQM)分別研究了功能梯度Timoshenko梁的穩(wěn)定性和彎曲變形問題。總之，數(shù)值方法是研究軸向功能梯度梁振動和穩(wěn)定性問題的主要手段。

研究提出采用微分求積法求解彈性地基上功能梯度Euler-Bernoulli梁的屈曲臨界荷載問題。基于Euler-Bernoulli梁理論建立了求解彈性地基上功能梯度Euler-Bernoulli梁屈曲臨界荷載的變系數(shù)微分方程，運用微分求積法理論，將該變系數(shù)常微分方程的特征值問題轉(zhuǎn)化為一組線性代數(shù)方程組的特征值問題，再由QR法可一次性地獲得彈性地基梁的屈曲臨界荷載。

1 計算模型

1.1 Euler-Bernoulli梁穩(wěn)定性的基本理論

彈性地基上功能梯度Euler-Bernoulli梁如圖1所示。考慮彈性地基上長度為

l

且材料性能和截面面積沿軸向

x

任意連續(xù)變化的Euler-Bernoulli梁，其撓度設(shè)為

w

(

x

,

t

)。假設(shè)材料的彈性模量為

E

(

x

)，材料的密度為

ρ

(

x

)，截面面積為

A

(

x

)，截面轉(zhuǎn)動慣量為

I

(

x

)，它們均為

x

的函數(shù)，即

E

(

x

)=

E

f

(

x

)，

ρ

(

x

)=

ρ

f

(

x

)，

I

(

x

)=

I

f

(

x

)，

A

(

x

)=

A

f

(

x

)。其中，

E

、

ρ

、

A

、

I

分別對應(yīng)于軸向功能梯度梁在左端邊界

x

=0位置材料的彈性模量、密度、截面積和截面慣性矩；

C

為地基彈性系數(shù)；設(shè)軸向力

P

>0為壓力，

P

<0為拉力，則荷載

P

作用下的功能梯度材料彈性地基Euler-Bernoulli梁的自由振動方程為：

圖1 彈性地基上功能梯度Euler-Bernoulli梁

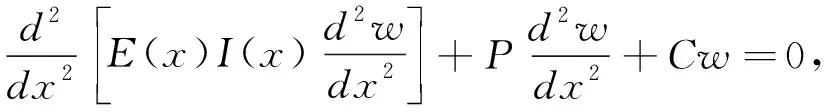
(1)

研究主要考慮梁的諧波振動問題，則有

w

(

x

，

t

)=

W

(

x

)sin

ωt

,

(2)

式中，

ω

為振動角頻率;

t

為時間;

w

(

x

,

t

)為撓度；

W

(

x

)為振型函數(shù)。將式(2)代入式(1)，可得軸向功能梯度Euler-Bernoulli梁在軸向力

P

作用下的振動方程為：

(3)

(4)

將式(4)代入式(3)，可得關(guān)于軸向功能梯度Euler-Bernoulli梁臨界屈曲荷載

λ

特征值的控制方程為：

(5)

1.2 Euler-Bernoulli梁的邊界條件

Euler-Bernoulli梁的轉(zhuǎn)角

θ

，彎矩

M

和剪力

T

分別為：

(6)

簡支-簡支梁(H-H)的邊界條件為：

θ

=0和

M

=0，

W

(0)=0,

W

(0)=0;

W

(1)=0,

W

(1)=0,

(7a)

固端-固端梁(C-C)的邊界條件為：

w

=0和

θ

=0，

W

(0)=0,

W

(0)=0;

W

(1)=0,

W

(1)=0,

(7b)

固端-簡支梁(C-H)的邊界條件為：

w

=0和

θ

=0、

θ

=0和

M

=0，

W

(0)=0,

W

(0)=0;

W

(1)=0,

W

(1)=0。

(7c)

因此，彈性地基上Euler-Bernoulli梁臨界屈曲荷載的計算可以轉(zhuǎn)化為在邊界條件式(7)下，常微分方程式(5)的特征值問題，研究采用微分求積法對此展開數(shù)值分析。

1.3 微分求積法分析

微分求積法的本質(zhì)是把函數(shù)在給定的離散點上的各階導(dǎo)數(shù)值，近似地用全域上所有網(wǎng)點處的函數(shù)值的加權(quán)和來表示。彈性地基上功能梯度Euler-Bernoulli梁的計算域為0≤

ξ

≤1，離散單元數(shù)為

n

，離散節(jié)點數(shù)為

n

+1，離散節(jié)點的分布采用切比雪夫多項式的根和等比數(shù)列兩種非均勻變步長布點方式。

(8a)

(8b)

根據(jù)微分求積規(guī)則，每個離散節(jié)點處對應(yīng)的函數(shù)導(dǎo)數(shù)為:

(9a)

(9b)

這里，權(quán)系數(shù)的定義為:

(10)

其中，權(quán)系數(shù)矩陣

A

()的各階導(dǎo)數(shù)之間的關(guān)系為:

A

(+1)=

A

A

()=

A

()

A

，(

r

≥1),

(11)

令

r

=0時，權(quán)系數(shù)矩陣

A

為單位矩陣

I

，則

(12)

將式(11)代入控制方程式(5)和不同邊界條件式(7)，得到相應(yīng)網(wǎng)格節(jié)點的微分求積近似離散為：

(13)

不失一般性，以兩端簡支梁(H-H)情況為例進行討論。將式(11)代入式(7a)，得

(14a)

(14b)

至此，聯(lián)立式(13)和式(14)，采用QR法求解一般廣義代數(shù)特征方程組，可得到在邊界條件H-H下，彈性地基上功能梯度Euler-Bernoulli梁的屈曲臨界荷載，其他邊界條件可類似獲解。

2 算例分析

對于長度為

l

的軸向功能梯度變截面Euler-Bernoulli梁，給出式(15a)、式(15b)、式(15c)三種情形的抗彎剛度

EI

(

x

)：

EI

(

x

)=

E

I

(1+

x

),

(15a)

EI

(

x

)=

E

I

(1+

x

),

(15b)

EI

(

x

)=

E

I

(1+

x

),

(15c)

這里，梁抗彎剛度沿軸向呈多項式函數(shù)變化，即

EI

(

x

)=

E

I

(1+

x

),(

k

=1,2,3)。

表1 梁的無量綱屈曲臨界荷載值(EI(x)=E0I0(1+x);c=0;n=32)

表2 梁的無量綱屈曲臨界荷載值(EI(x)=E0I0(1+x)2;c=0;n=32)

表3 梁的無量綱屈曲臨界荷載值(EI(x)=E0I0(1+x)3;c=0;n=32)

當

k

=2，即抗彎剛度

EI

(

x

)=

E

I

(1+

x

)時，考慮地基的影響，即

c

≠0，運用微分求積法求解功能梯度Euler-Bernoulli梁臨界荷載值，地基彈性系數(shù)分別取

c

=25、50、100，彈性地基梁的臨界荷載如表4所示。研究計算結(jié)果與文獻[9-10]完全吻合；不考慮地基的影響，即

c

=0，運用微分求積法求解功能梯度變截面Euler-Bernoulli梁臨界荷載值，功能梯度Euler-Bernoulli梁的前5階臨界荷載如表5所示。微分求積法計算值與文獻[9]和文獻[11]結(jié)果完全吻合，再次證明了微分求積法求解彈性地基上功能梯度Euler-Bernoulli梁臨界荷載的精確性。

表4 梁的無量綱屈曲臨界荷載值(EI(x)=E0I0(1+x)2;c≠0;n=32)

表5 梁的無量綱屈曲臨界荷載值(EI(x)=E0I0(1+x)2;c=0;n=32)

彈性地基梁抗彎剛度沿軸向呈多項式函數(shù)變化，即

EI

(

x

)=

E

I

(1+

x

)，(

k

=1,2,3)，梁左右兩端分別在C-C、C-H、H-H邊界條件下，對應(yīng)的無量綱臨界屈曲荷載隨無量綱地基彈性系數(shù)變化的關(guān)系曲線圖如圖2、圖3、圖4所示。由圖2、圖3、圖4計算結(jié)果可知，隨著地基彈性系數(shù)增大，臨界屈曲荷載近似呈線性增長；

k

值增大，反映了梁的抗彎剛度

EI

(

x

)沿軸向自左至右分別呈線性、二次與三次拋物線型變化，相應(yīng)的臨界屈曲荷載數(shù)值明顯增大，且邊界約束越強，其屈曲臨界荷載越高。綜上可知，彈性地基上Euler-Bernoulli梁的穩(wěn)定承載力與梁邊界條件、抗彎剛度、地基彈性約束強弱等因素密切相關(guān)。

圖2 屈曲臨界荷載λcr1與無量綱地基彈性系數(shù)c的關(guān)系曲線(n=32，q1=1.2，C-C邊界條件) 圖3 屈曲臨界荷載λcr1與無量綱地基彈性系數(shù)c的關(guān)系曲線(n=32，q1=1.2，C-H邊界條件)

圖4 屈曲臨界荷載λcr1與無量綱地基彈性系數(shù)c的關(guān)系曲線(n=32，q1=1.2，H-H邊界條件)

3 結(jié)論

基于Euler-Bernoulli梁理論，建立了在計算軸向力

P

作用下，求解彈性地基上功能梯度Euler-Bernoulli梁屈曲臨界荷載的控制方程，運用微分求積法理論，將變系數(shù)常微分方程的特征值問題轉(zhuǎn)化為線性代數(shù)方程組的特征值問題，一次性地獲得彈性地基上梁的屈曲臨界荷載。

軸向功能梯度變截面Euler-Bernoulli梁臨界荷載的控制方程是一組復(fù)雜的變系數(shù)常微分特征方程，研究方法避免了用迭代方法計算超越方程的困難和繁雜。研究可一次性地計算出彈性地基上功能梯度Euler-Bernoulli梁的臨界荷載，變步長等比數(shù)列和切比雪夫多項式的根兩種布點方式的計算精度等價，且計算值和已有文獻計算結(jié)果完全吻合，表明了微分求積法求解彈性地基上Euler-Bernoulli梁臨界荷載的可行性和精確性。

運用微分求積法計算的結(jié)果表明，彈性地基上Euler-Bernoulli梁的穩(wěn)定承載力與梁的邊界條件、抗彎剛度、地基彈性約束強弱等因素密切相關(guān)。