基于周期自適應學習的中低速磁懸浮列車運行控制方法

張文靜，南 楠，曹博文，李孟月，岳 強，徐洪澤

(北京交通大學 電子信息工程學院, 北京 100044)

磁懸浮列車是一種利用電磁力實現懸浮、導向與驅動的新型軌道交通工具，有望成為21世紀的主要交通方式之一。與傳統輪軌列車相比，磁懸浮列車具有振動小、運行噪音低、轉彎半徑小、抗風化能力強、壽命長等優點[1]。此外，由于采用非接觸式運行方式，磁懸浮列車取代了輪軌交通的輪軌接觸支撐結構，無附著力限制，爬坡能力更強。隨著上海磁懸浮試驗線、長沙機場快線和北京S1線的相繼開通，磁懸浮交通的運行控制成為軌道交通理論研究領域的熱點問題。

運行控制系統OCS(Operation Control System) 是保證磁浮列車正常運行的中樞系統，是磁浮列車運行控制的“大腦”和“神經系統”，主要作用是運行指揮和安全防護。運行控制算法是OCS的核心技術之一，然而目前的磁浮運行控制系統借鑒CBTC (Communication-Based Train Control System)系統，尚無成熟的運行控制算法。因此，研究磁懸浮列車運行控制算法，提高磁浮列車運行控制性能，具有重要的意義。

文獻[2-3]提出了不同的控制方法，有效地提高了輪軌列車的運行性能。文獻[4]結合專家經驗和梯度下降法，設計了一種基于在線調整方法的智能駕駛算法，提高了列車運行性能。文獻[5]改進了傳統的列車動力學模型，利用遺傳算法修正不同運行條件下的阻力系數，通過將分數階PID控制器引入列車運行控制，實現了更好的速度控制效果，提高了控制精度。為提高列車自動駕駛ATO(Automatic Train Operation)系統速度控制的精度與魯棒性，文獻[6]提出了一種基于模糊PID的ATO控制算法。針對列車停車階段的重復性和涉及多目標的特性，文獻[7]引入迭代學習控制ILC(Iterative Learning Control)，提高了列車停車精度與舒適度。以上均為基于輪軌交通系統的運行控制方法。然而，磁懸浮列車與傳統輪軌列車的牽引方式不同，其運行控制方法存在較大差異，現有成熟的輪軌列車運行控制方法并不適用于磁懸浮列車。

近年來，研究學者們將ILC用于重復作業對象，利用先前迭代或周期信息不斷修正當前迭代或者周期的控制器輸出，隨著迭代次數的增加，系統可以在有限時間內精確跟蹤期望軌跡[8-10]。文獻[11]提出了一種基函數型自適應迭代控制方法，提高了迭代學習控制下非最小相位系統的位置跟蹤精度。文獻[12]設計了一種約束自適應邊界迭代學習控制律，解決了周期邊界擾動下Euler-Bernoulli系統的振動控制和輸入約束問題。在文獻[13-15]中，針對具有周期擾動或具有周期性狀態變量的控制系統，引入周期自適應學習控制(Periodic Adaptive Learning Control,PALC)，取得了較好的控制效果。文獻[16]利用PALC算法補償電機系統中狀態相關的非Lipschitz周期擾動，實現了高精度的位置跟蹤。文獻[17]結合線性擾動觀測器和周期自適應學習的優點，提出了一種周期學習擾動觀測器，有效補償了永磁同步直線電機中的非線性干擾。文獻[18]針對永磁同步位置伺服系統中的周期性擾動補償問題，設計了一種雙高階周期自適應學習補償方法，提高了系統的位置跟蹤性能。文獻[19]利用PALC算法及飽和補償器，實現了飽和輸入非線性系統的高精度位置跟蹤控制。

中低速磁懸浮列車運行速度較低(≤160 km/h)，主要阻力來源于渦流阻力和特殊線路段的線路附加阻力。由于線路的坡道和彎道是固定的，當列車在指定線路往返運行時，所受運行阻力具有周期性。通過分析列車動力學模型，本文將周期自適應學習引入列車運行控制，提出一種基于周期自適應學習的列車運行控制方法。控制器包括4個部分：PD控制模塊、速度前饋模塊、渦流阻力與空氣阻力補償模塊和周期自適應線路附加阻力補償模塊。本文所提出的運行控制方法的核心是：利用PALC算法估計運行過程中的線路附加阻力，在控制器中加入相應的控制力(包括牽引力和制動力)，消除線路附加阻力對列車運行的影響，提高列車運行的性能。仿真結果驗證了本文所提控制算法的有效性與魯棒性。

1 中低速磁懸浮列車運行控制問題描述

根據牛頓運動定律,在磁懸浮列車運行過程中,列車所受合力滿足[20]

ma=u-fair-feddy-fi-fr

(1)

式中：m為列車質量；a為列車加速度；u為列車牽引力或制動力；fair為列車運行過程中所受到的空氣阻力；fi和fr分別為坡道附加阻力和彎道附加阻力；feddy為線路F軌與懸浮電磁鐵間的渦流阻力。

列車運行過程中，所受空氣阻力與列車車體的最大橫截面積、阻力系數、空氣密度以及列車速度有關，可表示為

(2)

式中：v為列車速度；N為列車編組車輛數。

懸浮系統的電磁鐵芯由硅鋼薄片疊壓而成，其渦流效應可以忽略不計。渦流阻力主要來自于線路兩側的F軌與懸浮電磁鐵之間的渦流效應，計算式為

feddy=N(0.1v0.5+0.02v0.7)

(3)

當磁懸浮列車經過坡道線路時,坡道附加阻力大小由坡道坡度決定，可表示為

fi=iNmgsgnφ

(4)

式中：i為坡道坡度的千分度；g為重力加速度。當sgnφ>0時，表示列車處于上坡狀態，fi>0；當sgnφ<0時，表示列車處于下坡狀態，fi<0。

此外，當列車運行于彎道線路時，所受的彎道附加阻力可表示為

(5)

式中：R為彎道線路曲線半徑。

考慮如下的中低速磁懸浮列車動力學模型

(6)

(7)

式中：x(t)為列車位移；fres[x(t)]sgn[v(t)]是磁懸浮列車在運行過程中受到的線路附加阻力，包括彎道附加阻力與坡道附加阻力，不考慮管道附加阻力。

假設1 當列車的運行控制性能較高且沿固定線路往返運行時，列車的位置與速度均有相同且固定的周期Pt，且Pt可以準確獲得，列車的位置與速度滿足xd(t+iPt)=xd(t)，vd(t+iPt)=vd(t)，x(t+iPt)≈x(t)，v(t+iPt)≈v(t)，i∈Z+。

性質1 在列車運行過程中，所受線路附加阻力的大小與列車實際位置x有關。根據假設1，線路附加阻力fres滿足:fres(t+iPt)≈fres(t)，i∈Z+。

為了提高列車運行控制性能，利用列車運行和運行阻力共有的周期特性，本文提出一種基于周期自適應學習的列車運行控制方法。

2 周期自適應學習控制器設計

通常，列車在指定線路第一次往返運行時，駕駛員可以利用駕駛員控制臺(Driver Control,DC)顯示的線路信息(包括線路最高限速、列車當前速度等)和車輛狀態，依據實際情況進行操作，實現手動駕駛。從列車第二次往返開始，利用前一周期的信息和PALC算法，估計運行過程中的線路附加阻力。

(1)實際的列控系統為復雜、多目標的非線性動力系統，為保證第一周期系統穩定，讓有長期駕駛經驗的司機駕駛，可以實時有效地控制列車滿足多項要求[2]。

ex(t)=x(t)-xd(t)

(8)

(9)

e=ev(t)+λex(t)

(10)

式中：λ為待調節正參數;ex為位置誤差；ev為速度誤差。

(11)

為了消除運行阻力對系統的影響，針對運行阻力中的未知參數fres(x)，結合自適應理論與列車運行的周期特性，本文設計了周期學習自適應控制器為

(12)

式中：α為待設計正參數。

圖1 PALC自適應控制律結構框圖

從第2個周期開始,利用周期自適應更新律,開始學習未知參數fres為

(13)

式中：kres為待設計周期自適應增益；P(t)為列車運行周期。

為證明系統的穩定性，構造Lyapunov函數為

(14)

計算V(t)在周期區間[t-Pt，t]的差分為

(15)

為使計算過程清晰，令式(15)右邊第一項為A，第二項為B，即

(16)

(17)

由式(7)和式(9)可知

(18)

由式(10)和式(12),可得

(19)

將式(19)代入式(16)，A簡化為

α(ev+λex)2]dτ

(20)

由列車運行的周期性和性質1，可得

(21)

將式(20)和式(21)代入式(15)，化簡可得

ΔV=A+B=

(22)

代入自適應更新律式(13)，式(22)右邊第二項等于0。因此，有

(23)

3 仿真驗證

利用某中低速磁懸浮試驗線數據進行仿真研究，通過與傳統PID控制器的對比，驗證所提出算法的優越性和有效性，試驗線路見圖2，試驗線車輛參數見表1。

圖2 中低速磁懸浮列車試驗線路(單位：m)

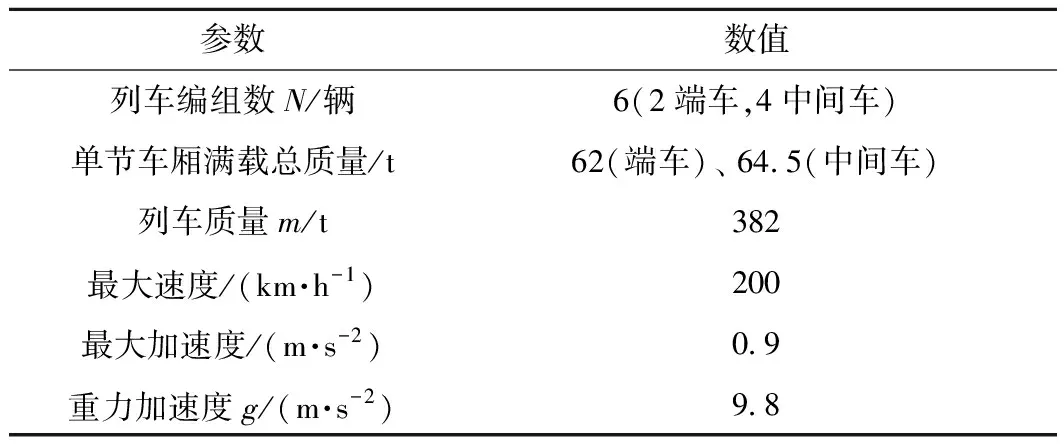
表1 車輛與線路參數

3.1 參數調節

仿真時，PALC控制器和PID控制器的參數調節過程如下

Step1線性參數調節。綜合考慮系統快速性和平穩性，利用MATLAB工具箱整定PALC控制器和PID控制器參數，結果見表2。

表2 PALC和PID控制器的線性部分參數

Step2自適應參數調節。理論上，自適應參數可選擇任意正數，數值越大，收斂速度越快，跟蹤誤差越小。然而，過大的參數會導致系統震蕩甚至不穩定。因此，綜合考慮系統的收斂速度、穩定性和跟蹤誤差，通過多次調節，選擇使PALC控制器控制效果最佳的自適應參數為kres=2×1012。

3.2 仿真驗證

在仿真中，令初始狀態為零，從第二個周期開始，利用周期自適應更新律，對線路附加阻力進行估計。設置仿真中列車單程運行距離1.58 km，最大加速度為0.9 m/s2，往返周期Pt=178 s，仿真步長T=10-5s。

設置的期望速度-位置曲線見圖3，期望位置曲線xd、PID控制器和PALC控制器的位置跟蹤軌跡見圖4，PID控制器和PALC控制器的位置跟蹤誤差見圖5。可以看出，由于存在線路附加阻力，PID控制器的最大位置跟蹤誤差為3.12 m。PALC控制器充分利用了列車往返運行過程中的周期信息，在16個迭代周期后，最大位置誤差僅為0.03 m，從圖5中可以看出，PALC控制器具有更好的位置跟蹤性能。

圖3 期望速度-位置曲線

圖4 期望位置曲線及PALC控制器和PID控制器的位置跟蹤曲線

圖5 PALC控制器和PID控制器的位置跟蹤誤差

PID控制器和PALC控制器的速度跟蹤以及速度跟蹤誤差曲線分別見圖6和圖7，在不同線路的速度跟蹤誤差列于表3。從仿真結果可以看出，在平直線路，由于僅存在渦流阻力，PALC和PID控制下的速度跟蹤性能差別不大。然而，在彎道線路與坡道線路，相對于PID控制器，由于PALC控制器補償了線路阻力，其速度跟蹤性能更好。另外，從圖6可以看出，PALC控制下的列車速度跟蹤曲線更加平滑，列車運行更加平穩，舒適性更好。

圖6 PALC控制器和PID控制器的速度曲線

圖7 PALC控制器和PID控制器的速度跟蹤誤差

PALC算法估計的附加阻力和真實線路附加阻力見圖8。可以看出，在16個迭代周期后，PALC控制器成功的估計了線路附加阻力。

圖8 實際附加阻力和PALC算法估計線路阻力

PID控制器和PALC控制器的控制輸出曲線見圖9。由圖9可以看出，經過16個迭代周期，PALC控制器輸出穩定。PALC控制器和PID控制器下列車在第17個運行周期內的能耗曲線見圖10。由圖10可以看出，與PID控制器相比，PALC控制器控制下的磁浮列車，不僅位置跟蹤性能更優，而且能耗降低了0.2%。

圖9 PALC控制器和PID控制器的輸出

圖10 第17個運行周期內的列車運行能耗曲線

為了驗證所提出算法的優越性，利用位置誤差的ITAE指標，比較PALC控制器和PID控制器的位置跟蹤性能，結果見圖11。由圖11可以看出，PALC算法消除了線路附加阻力對列車位置跟蹤性能的影響。

圖11 PALC控制器和PID控制器的位置誤差ITAE指標

為了進一步檢驗本文所提PALC算法的魯棒性，在控制器參數不變的情況下，加入能量譜密度為1012的白噪聲干擾。噪聲干擾下的位置跟蹤誤差、速度跟蹤誤差、控制器輸出以及線路附加阻力估計曲線見圖12。從圖12中可以看出，加入噪聲干擾后，列車在PID控制器和PALC控制器下的最大位置跟蹤誤差分別為3.22、0.01 m，在不同線路區段最大速度誤差跟蹤見表4。對比無噪聲干擾下的仿真結果，PID控制下的列車速度與位置跟蹤性能明顯變差，而PALC控制下的列車速度與位置跟蹤性能下降很小，表明PALC控制器有較強的魯棒性。

表4 噪聲干擾下不同線路區段的最大速度跟蹤誤差 m/s

圖12 噪聲干擾下PALC控制和PID控制的位置跟蹤誤差、速度跟蹤誤差、控制器輸出及線路附加阻力估計曲線

4 結論

針對中低速磁懸列車的位置控制問題，本文考慮列車在指定線路運行的周期特性，提出了基于周期自適應學習的運行控制算法，消除了運行阻力對列車運行過程的影響，提高了列車位置控制的性能。該控制方法包含4部分：PD部分保證系統滿足基本控制要求，前饋部分改善了系統瞬態響應，周期自適應補償部分實時估計線路附加阻力，空氣阻力與渦流阻力補償部分進一步提高了列車的位置跟蹤性能。仿真結果表明：本文所提出的周期自適應運行控制方法能夠有效提高中低速磁浮列車運行的位置控制精度，控制算法具有較強的魯棒性，而且能耗更低。