動車組車輪多邊形磨耗發展歷程模擬及車輪粗糙度的影響

宋志坤，任海星，胡曉依，劉元富,劉 偉,李 強

(1.北京交通大學 機械與電子控制工程學院， 北京 100044；2.中國鐵道科學研究院集團有限公司鐵道科學技術研究發展中心， 北京 100081)

近年來，我國動車組出現了車輪多邊形化現象，當運行速度為300 km/h時，車輪表現出18～20階多邊形化[1]，當運行速度為250 km/h時，車輪多邊形的主要階次為23、24階[2]，高階車輪多邊形磨耗導致軌道和車輛系統中的諸多問題。一方面，車輪多邊形會產生高頻輪軌沖擊載荷，導致轉向架零部件發生損壞或者失效，對動車組行駛安全產生重要影響。另一方面，車內噪聲在300～400、500～600 Hz頻率范圍內存在聲共振區域，一定車速下，車輪多邊形磨耗激勵頻率處于此頻段時，會使車輛系統的振動水平升高，進而激勵車體內裝板振動，產生振動輻射噪聲[3]。因此，不得不在達到鏇修里程前對車輪進行鏇修，這縮短了車輪的使用壽命，增加了我國高速鐵路的運營成本。

只有掌握車輪多邊形的形成規律，才能從根本上控制高階多邊形的產生和發展。文獻[4]分析了高速下理想1階到5階初始多邊形磨耗的發展，結果發現多邊形磨耗的發展很大程度上取決于軌道特征和激勵頻率。文獻[5]利用車輛/軌道耦合動力學模型結合Archad磨耗模型，研究了地鐵列車在直線軌道上的多邊形演化歷程。結果表明，5～7、14～20階多邊形的增長幅度最大。前者被認為與車輛/軌道耦合系統垂直共振有關，后者可能是由軌道垂直反振引起的。文獻[6]通過試驗研究了地鐵車輪多邊形磨耗的影響因素及增長規律，得出地鐵車輪的9階多邊形磨耗是由于輪對的一階彎曲振動引起的。文獻[7]研究了輪對柔性對多邊形磨耗的影響，發現在急彎軌道上，輪對的扭轉模態可以促進多邊磨耗的發展，而輪對彎曲模態對多邊形磨耗沒有促進作用。文獻[8]指出輪軌系統摩擦自激振動是導致車輪多邊形的主要原因之一。文獻[9]研究發現車輪之間鋼軌的三階垂向彎曲共振，導致輪軌法向力在550～650 Hz之間周期性波動，是導致車輪多邊形產生的主要原因。

目前，研究人員主要是通過試驗與仿真的方法對車輪多邊形產生機理進行相關的研究，對車輪多邊形發展的整個歷程及影響因素研究比較少。從實際應用的角度來看，確定車輪多邊形磨耗發展的影響因素，進而提出相應的抑制措施具有重要的現實意義。

為了研究動車組車輪多邊形磨耗發展的影響因素，本文建立考慮柔性輪對和柔性軌道的車輛/軌道耦合動力學模型，將其與Archard磨耗模型相結合建立長期磨損迭代模型。模擬動車組車輪多邊形產生和發展的全過程，創造性地從車輪多邊形整個發展歷程的角度研究車輪粗糙度對車輪多邊形發展的影響。

1 長期磨損迭代模型的建立

1.1 車輛/軌道耦合動力學模型

由于車輪多邊形的激勵頻率通常較高，傳統的多剛體動力學模型覆蓋的頻率有限，難以滿足仿真要求，因此結合有限元軟件Ansys與多體動力學軟件SIMPACK建立考慮柔性輪對和柔性軌道的車輛/軌道耦合動力學模型[10]。

首先使用多體動力學軟件SIMPACK，以某型動車組為研究對象，建立多剛體動力學模型。建立輪對的有限元模型如圖1所示。將車輪與車軸視為整體部件，不考慮車輪與車軸的過盈配合關系。整體輪對采用六面體網格劃分，單元類型為3D實體單元Solid45。車輪直徑為920 mm，踏面廓形為S1002CN，輪對的彈性模量為2.1×105MPa，泊松比為0.3，密度為7.85×103kg/m3。將構建好的柔性輪對模型通過SIMPACK中的FLEXBODY模塊導入替換掉剛性輪對。

圖1 輪對有限元模型

建立柔性軌道不僅需要建立鋼軌的有限元模型，還需要編寫柔性軌道的配置文件，利用SIMPACK軟件中的FLEXTRACK模塊讀取配置文件以實現柔性軌道的導入。鋼軌廓形采用60 N型鋼軌，軌枕間距為0.63 m，軌枕、扣件、道床等軌下結構統一采用彈簧阻尼元件模擬，鋼軌的彈性模量、密度、泊松比等參數設置與輪對保持一致，軌道端部采用大剛度、大阻尼進行固定。最終獲得的車輛動力學模型見圖3。

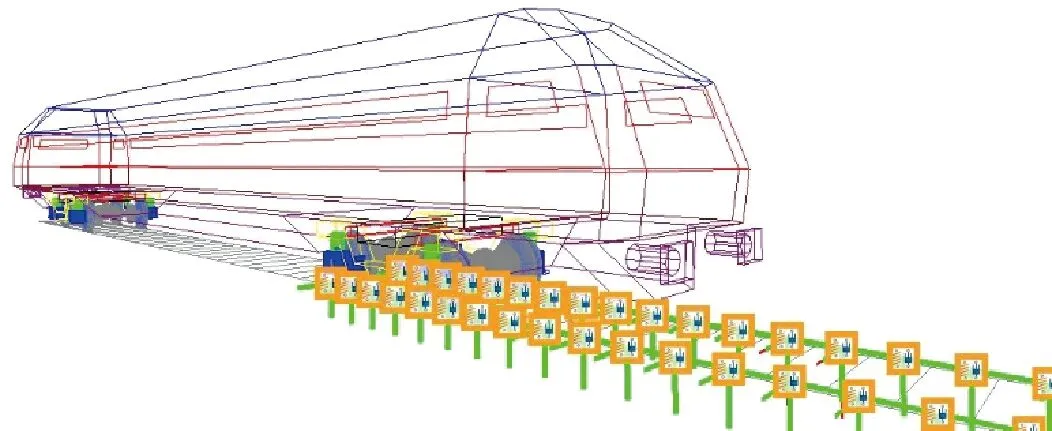
圖2 車輛/軌道耦合動力學模型

1.2 輪軌接觸模型

為了研究動車組在運行過程中的高頻振動，建立考慮柔性軌道和柔性輪對的車輛/軌道耦合動力學模型，輪軌接觸幾何計算仍然按照傳統的輪軌接觸幾何方法——跡線法[11]進行計算，輪軌法向接觸問題采用Hertz接觸理論進行計算，輪軌切向接觸問題采用FASTSIM算法進行計算。

在車輛動力學模型中，普遍把Hertz理論應用于法向接觸問題的求解，這是因為在很多情況下，采用Hertz理論計算法向接觸問題速度較快且精度也滿足要求。用于輪軌切向力計算的滾動接觸蠕滑率/力模型中大多數是基于Hertz接觸理論。因此，本文也采用Hertz接觸理論，假設輪軌接觸斑為橢圓。

(1)

根據彈性力學和靜電勢問題相似的假設，可以將橢圓接觸斑內的壓應力看作根據半橢球高度的坐標來變化，因此接觸斑內的壓應力分布可以表示為

(2)

式中：pz(x,y)為接觸斑內坐標為(x,y)的點承受的壓應力；N為輪軌法向力；a、b分別為橢圓的縱、橫向半軸長。

對于切向接觸問題，采用FASTSIM算法[12]，在該算法中法向應力分布與Hertz理論中法向應力半橢球式的分布有所不同，若把Hertz理論中的法向應力分布應用于FASTSIM算法中會產生較大的誤差。因此Kalker從Hertz理論中提取a、b，提出了適合FASTSIM算法的法向應力計算式為

(3)

為了便于計算接觸斑內切應力以及滑動速度分布，需要將接觸斑離散為多個單元，每個單元內壓應力、切應力以及滑動速度等參數保持一致。文獻[13]認為將接觸斑劃分為10×10個單元就可以比較合理地區分出黏著區和蠕滑區以及壓應力、切應力的分布情況。文獻[14]研究表明，計算精度隨著單元格劃分數量的增加而提高。因此將接觸斑沿縱、橫向均勻劃分為100×100個單元，單元格縱、橫向長度分別為Δx、Δy。

1.3 磨耗模型

在眾多計算磨耗模型中，Archard磨耗模型因為其較快的計算速度和較好的計算精度被廣泛采用，Archard磨耗模型的定義為

(4)

式中：Vwear為磨耗材料體積；Kw為無量綱的磨耗系數，由接觸壓力和相對滑動速度共同決定；N為兩物體間的法向接觸力；d為兩接觸物體的相對滑動距離；H為兩接觸物體中較軟材料的硬度，在本文中為車輪表面硬度。對于踏面磨耗，磨耗系數在1×10-4～10×10-4范圍內，對于輪緣磨耗，磨耗系數在1×10-4～400×10-4之間變化[8]。本文僅研究動車組在直線軌道上的運行情況，輪軌間相對滑動較小，因此假設磨耗系數為常數，取為1×10-4。

為了深入研究接觸斑內磨耗分布情況，可將Archard磨耗模型結合FASTSIM算法得出接觸斑內磨耗深度的計算式為

(5)

式中：Δz(x,y)為中心坐標為(x,y)的單元格的磨耗深度；ξ1、ξ2、ξ3分別為縱向、橫向、自旋蠕滑率；ux、uy分別為縱向、橫向的彈性滑動量。

使用Matlab編寫程序建立磨耗模型，提取車輛/軌道耦合動力學模型計算出的動力學數據，將其代入到磨耗模型中，計算出接觸斑內磨耗深度分布見圖3。磨耗深度為0的區域是黏著區，不為0的區域是蠕滑區，在黏著區和蠕滑區的交界處磨耗深度達到最大，在黏著區的末端磨耗深度趨于0。

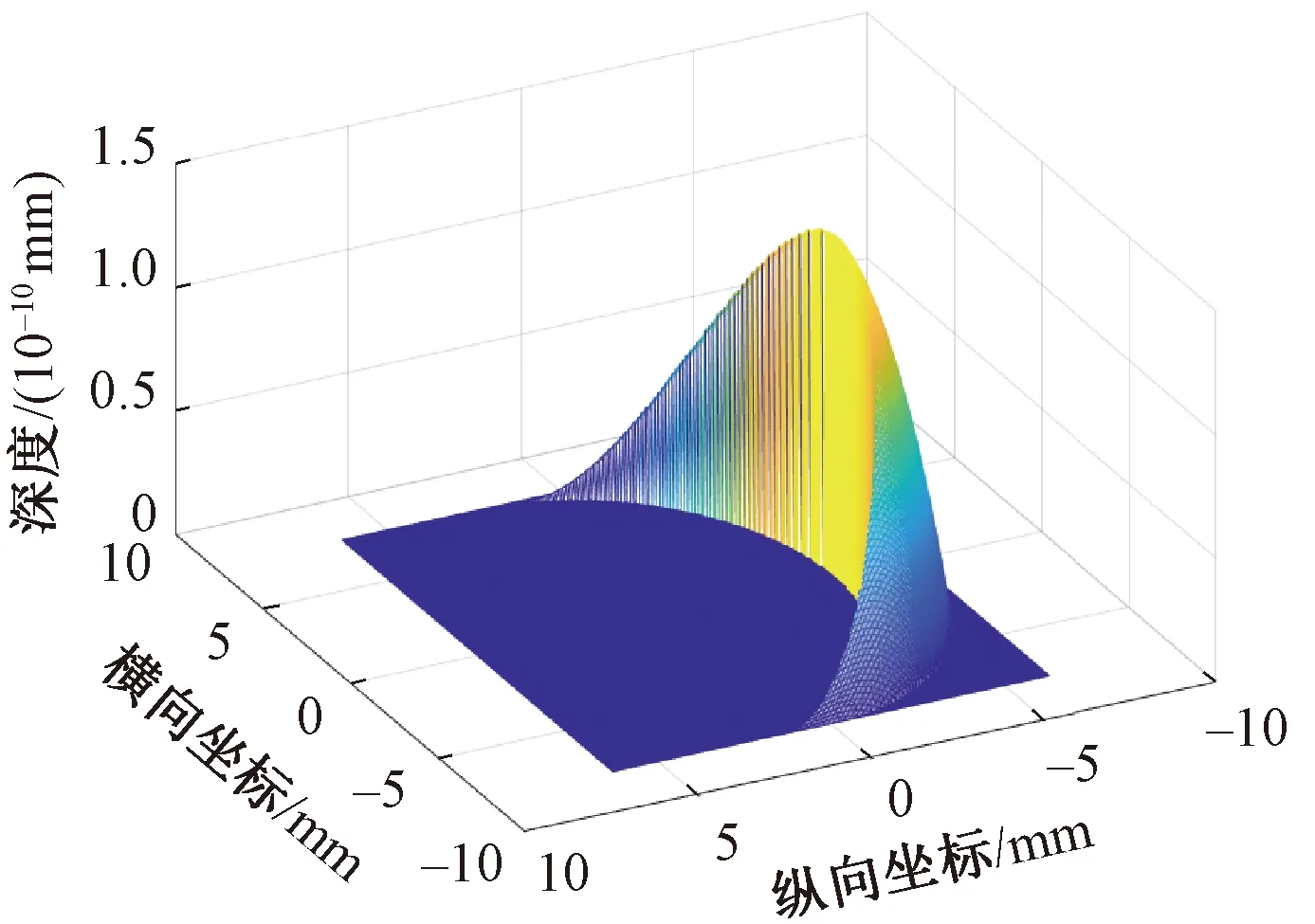
圖3 接觸斑內磨耗深度分布

2 車輪多邊形發展歷程模擬

為研究車輪圓周上磨耗分布情況，將車輪滾動圓均勻離散為3 600個點，每兩個采樣點之間相隔0.1°，對接觸斑內的磨耗深度進行縱向疊加，取平均值表示車輪旋轉一圈產生的磨耗積累量。

(6)

式中：Δzk為滾動圓上第k個離散點的磨耗深度；Δz(i,j)為接觸斑上縱向第i、橫向第j個網格的磨耗深度；MM為接觸斑縱向劃分的網格數；NN為接觸斑橫向劃分的網格數。

計算完這3 600個采樣點的磨耗量后使用40階傅里葉級數對磨耗進行擬合，可以獲得車輪圓周上的磨耗情況，傅里葉級數表達式為

x∈(0,2π)

(7)

式中：N為傅里葉級數的階次，高階車輪多邊形的階次一般不超過30，因此，本文N取40。

假設在短距離運行中車輪的磨耗累積量與行駛距離成線性增長，可以將車輪旋轉一圈產生的磨耗量乘以放大系數用來表示車輪運行一段距離產生的磨耗量。文獻[8]在計算時放大系數取1×106。一般來講，放大系數的取值越小，計算出的結果與實際越相符。因此，本文中放大系數取2×105，即動車組運行578 km產生的磨耗累積量。以初始車輪多邊形減去這個磨耗量獲得一個新的車輪多邊形，將這個新的多邊形代入到車輛動力學模型中，不斷重復上述過程就可以獲得車輛長距離運行中車輪多邊形的發展過程，這個迭代多次以獲取車輪多邊形長期磨耗的模型被稱之為長期磨損迭代模型。

使用長期磨損迭代模型，以實測初始車輪多邊形作為輸入，未考慮軌道不平順，模擬動車組運行速度分別為250、300 km/h時，車輪多邊形的發展歷程，磨耗累積量的極坐標分布見圖4。應用40階傅里葉級數對車輪多邊形進行擬合，利用車輪踏面粗糙度水平計算公式得出車輪表面粗糙度的階次變化圖。粗糙度水平計算式為

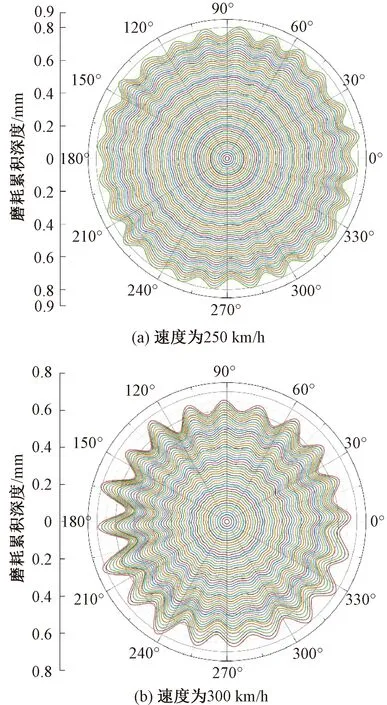
圖4 速度為250、300 km/h磨耗累積

(8)

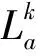
速度為250、300 km/h粗糙度水平階次變化見圖5。

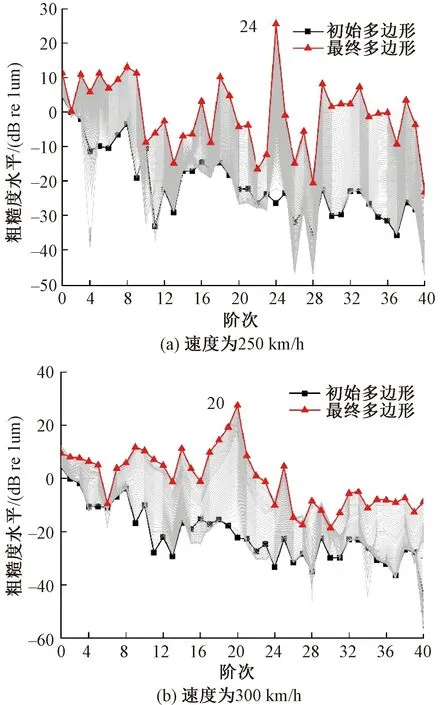
圖5 速度為250、300 km/h粗糙度水平階次變化

文獻[2]現場試驗發現當列車以速度250 km/h運行時產生的車輪多邊形階次為23、24階；當列車運行速度為300 km/h時，文獻[1]對不同輪徑下車輪多邊形階次進行統計分析發現，輪徑為860～890 mm的車輪主要由19階多邊形磨耗主導，而輪徑為900～920 mm的車輪主要由20階多邊形磨耗主導。

由圖5(a)可知，當動車組以250 km/h速度運行時，車輪多邊形最終以24階主導。由圖5(b)可知，當動車組以速度300 km/h運行時，車輪多邊形最終以20階主導。這一現象與動車組實際運行中產生的多邊形特征相吻合，驗證了長期磨損迭代模型的正確性。

根據實測數據與仿真結果發現，當動車組以250、300 km/h速度運行時，最終產生的車輪多邊形主導階次分別為20、24。頻率計算式為

(9)

式中：f為激勵頻率；n為多邊形階次；v為動車組運行速度；r為車輪名義滾動圓半徑。

由式(9)計算得出多邊形導致的激勵頻率約為580 Hz，說明在輪對和鋼軌之間存在一個固定的振動頻率，其應屬于結構模態頻率，這個振動頻率的存在促進了車輪多邊形的產生和發展。由式(9)可以發現，多邊形最終發展的階次與動車組運行速度有關，隨著速度的改變，多邊形的主導階次會隨之發生改變。

3 車輪粗糙度的影響

本文通過長期磨損迭代模型模擬動車組以250、300 km/h速度運行一段距離車輪多邊形的發展情況，結果與實際情況相吻合。因此可采用該模型深入研究車輪粗糙度對車輪多邊形發展歷程的影響。

動車組在長時間運行后，車輪上會產生多種磨耗損傷，包括車輪多邊形、踏面磨耗與輪緣磨耗等，這會導致動車組在運行過程中異常振動，影響行車安全。因此需要定期對車輪進行鏇修，但由于鏇修裝置以及各種人為原因導致鏇修后的車輪周向并不是完美的正圓，仍然存在一些多邊形，這可能會對車輪多邊形的發展產生影響。因此本文選取了鏇修質量不同的車輪上存在的兩種初始車輪多邊形，使用長期磨損迭代模型研究其對車輪多邊形發展的影響。鏇修質量不同的兩種初始多邊形見圖6，其中鏇修質量較差的車輪殘留了高階多邊形。

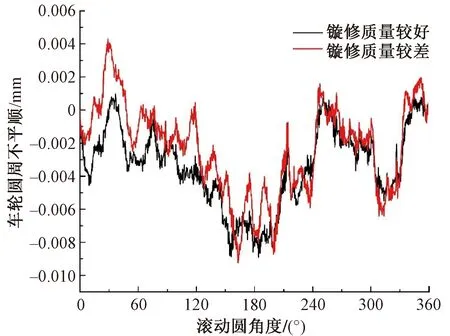
圖6 兩種不同鏇修質量的車輪多邊形

將這兩種初始車輪多邊形作為輸入，未考慮軌道不平順，分別計算其車輪多邊形的發展情況。運行速度設置為300 km/h，進行30次迭代后的發展情況見圖7。由圖7可見，鏇修質量較差的車輪粗糙度水平在24 dB附近，鏇修質量較好的車輪粗糙度水平在16 dB附近。對比之下可以發現，對于鏇修質量較差的車輪，多邊形發展速度比鏇修質量較好的車輪更快，導致最終車輪多邊形的粗糙度水平也更高。因此，提升鏇修質量，控制初始車輪不平順對于抑制車輪多邊形具有重要的作用。

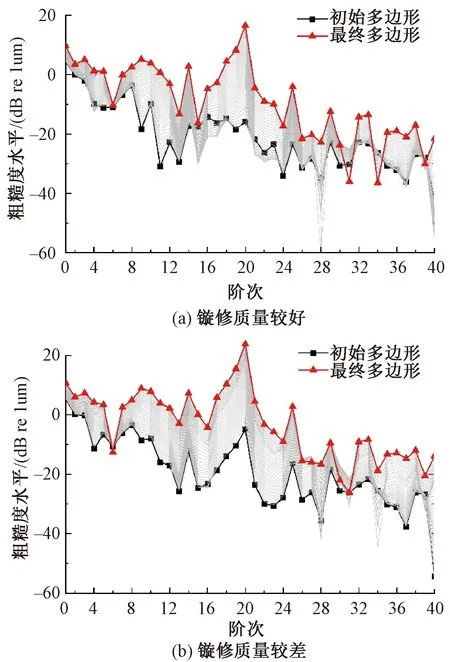
圖7 兩種鏇修質量下粗糙度水平發展過程

4 結論

本文建立考慮柔性輪對與柔性軌道的車輛/軌道耦合動力學模型，利用Matlab與SIMPACK聯合仿真將動力學模型與Archard磨耗模型相結合，建立長期磨損迭代模型。使用長期磨損迭代模型研究速度變化對車輪多邊形發展的影響，創造性地從車輪多邊形的整個發展歷程角度分析車輪粗糙度對車輪多邊形發展的影響，得到如下結論：

(1)使用長期磨損迭代模型模擬了動車組運行速度為250、300 km/h時車輪多邊形的整個發展歷程，發現車輪由最初無明顯高階多邊形發展到分別以24、20階多邊形占主導，這一現象與動車組實際運行過程中產生的車輪多邊形特性相似，驗證了長期磨損迭代模型的正確性。

(2)使用頻率計算公式發現，車輪多邊形的激勵頻率約為580 Hz，這說明在輪對和鋼軌之間存在一個固定的振動頻率，這個振動頻率的存在促進了車輪多邊形的產生和發展。

(3)車輪初始多邊形中是否殘留著高階多邊形是衡量鏇修質量好壞的一個重要指標，對比研究了鏇修質量的好壞對車輪多邊形發展的影響，結果發現在相同條件下提高鏇修質量可以在一定程度上抑制車輪多邊形的發展速度。