具有耦合分支的兩轉動兩移動并聯機構分析與優化

溫如鳳 方躍法 葉 偉

(1.北京交通大學機械與電子控制工程學院， 北京 100044； 2.山東管理學院智能工程學院, 濟南 250357；3.浙江理工大學機械與自動控制學院, 杭州 310018)

0 引言

傳統并聯機構的動平臺通過兩條以上分支與基座相連，具有多閉環結構。這類機構具有剛度好、負載能力強、操作速度快等優點，在分揀、運動模擬等領域得到了成功應用。但是，傳統的并聯機構中各分支獨立支撐動平臺，容易產生奇異位形、剛度退化等問題[1]。為此，學者們在并聯機構的分支間添加耦合分支，提出了廣義并聯機構的概念[2]。

相較于傳統并聯機構，具有耦合分支的廣義并聯機構在剛度、精度等方面更具優勢[3-4]。TIAN等[4]結合拓撲圖與螺旋理論提出了一種系統的綜合方法，用于含耦合分支并聯機構的構型綜合。DING等[5-6]設計了一類具有耦合分支的雙層雙閉環空間機構。劉婧芳等[7]在3-(RRR)RR并聯機構上添加耦合分支，得到了一類三移動自由度空間多環耦合機構。SHEN等[8]對并聯機構的分支進行拆分組合，設計了一類多環耦合六自由度機構。

在眾多少自由度機構中，動平臺輸出兩轉動兩移動運動(2R2T)的機構一直被廣泛關注。這類機構在加工機械[9-10]、農業機械[11]、醫療手術器械[12]等領域具有潛在的應用前景。YE等[13]設計了一類具有對稱分支結構的2R2T并聯機構。WANG等[14]采用鉸接動平臺設計了一類大轉動工作空間的2R2T并聯機構，并進行了性能分析。張彥斌等[15]基于螺旋理論設計了一類具有運動解耦特點的2R2T并聯機構。GAN等[16]對一種2R2T并聯機構進行了無奇異優化設計。范彩霞等[17]基于構型演變和李群理論進行了2R2T并聯機構構型綜合。

目前，已有較多含耦合分支的廣義并聯機構以及2R2T并聯機構的相關研究成果。但含耦合分支的2R2T并聯機構尚未見相關研究報道。本文提出一種具有耦合分支的2R2T并聯機構，基于李群理論進行自由度分析，然后進行運動學建模、剛度分析與優化設計，為機構的實際應用奠定理論基礎。

1 機構描述與自由度分析

圖1、2為本文提出的一種具有耦合分支的并聯機構。該機構動平臺和基座間有3條分支。分支1和分支2是RPU分支，其中R表示轉動副、P表示移動副、U表示虎克鉸。分支3是SPS分支，其中S代表球副。在分支1和分支2之間橫向連接了1條結構為RPR的耦合分支4。分支1、2、4中所有的轉動副軸線與虎克鉸的第1條轉軸平行，且與這些分支中移動副的軸線垂直。分支1和2內2個虎克鉸的第2條轉軸共線。

用A1和A2分別表示分支1和分支2與基座相連轉動副的中心，A3表示分支3與基座相連球副的中心。類似地，用B1和B2分別表示分支1和分支2與動平臺相連虎克鉸的中心，B3表示分支3與動平臺相連球副的中心。C1和C2分別表示耦合分支4與分支1和分支2相連轉動副的中心。點A1、A2、A3位于同一平面內，且構成一個等腰三角形。線段A1A3與A2A3等長，A1A2長度等于2a，A3與A1A2的垂直距離等于a。動平臺B1B2B3同樣設計為等腰三角形，線段B1B3與B2B3等長，B1B2長度等于2b，B3與B1B2的垂直距離等于b。線段B1C1與B2C2等長，長度均為c。在基座上建立定坐標系oxyz，原點o位于線段A1A2中點，x軸沿oA2方向，y軸沿oA3方向，z軸遵從右手法則。同樣，在動平臺上建立動坐標系puvw，原點p位于線段B1B2中點，u軸沿oB2方向，v軸沿oB3方向，w軸遵從右手法則。

采用李群理論[18]對機構進行自由度分析。注意到C1和C2分別是分支1和分支2上的點，由于分支1和分支2結構的限制，這兩個點始終位于xoz平面內，它們的相對自由度為平面內的兩個移動和一個轉動。耦合分支4為RPR結構，構成三維位移子群{G(y)}，允許xoz平面內的所有3個自由度。因此，耦合分支4的引入對點C1和C2的相對自由度沒有影響，也就意味著對整體機構的自由度沒有影響。

根據以上分析，可將耦合分支4移除，再分析動平臺的自由度特性。分支1位移流形L1可表示為

L1={R(A1,y)}{T(a1b1)}{R(B1,y)}{R(B1,u)}={G(y)}{R(B1,u)}

(1)

式中 {R(A1,y)}——軸線平行于y軸且通過點A1的轉動位移子群

{T(a1b1)}——沿向量a1b1方向的移動位移子群

a1b1——沿分支1內移動副方向的單位向量

{G(y)}——垂直于y軸的平面位移子群

其余符號含義類同。

分支2和分支1結構相同，且由于點B1和點B2均位于u軸上，分支2位移流形L2可以表示為

L2={G(y)}{R(B2,u)}={G(y)}{R(B1,u)}

(2)

分支3為SPS分支，有6個自由度，其位移流形L3是六維李群，記為

L3={D}

(3)

可得動平臺位移流形{M}為

{M}=L1∩L2∩L3={G(y)}{R(B1,u)}∩{G(y)}{R(B1,u)}∩{D}={G(y)}{R(B1,u)}

(4)

由式(4)可知，該機構動平臺有4個自由度，包括xoz平面內2個移動自由度、繞y軸的轉動自由度、繞u軸的轉動自由度。由于位移子群和子流形表示連續運動，機構的4個自由度也是連續自由度。

為了使機構具有確定的運動，需要選取4個關節作為主動關節。選取機構內4個移動副作為主動關節。如果鎖住所有的主動關節后，機構的自由度為0，說明驅動選取合適。觀察機構的結構，可發現動平臺繞u軸的轉動自由度完全由分支3控制，與分支1、2、4無關。而分支1、2、4與動平臺實際構成一個平面子機構，圖3為鎖住主動關節后的該平面子機構。此時，構件數為4，低副數目為6，機構的自由度F=3×4-2×6=0，表明分支1、2、4中的主動關節能完全控制線段B1B2在空間的位姿。

當B1B2的位姿確定后(即可視為與基座相連)，鎖定分支3內主動關節后，動平臺與分支3構成的局部子機構如圖4所示，其中，構件數為2，轉動副數目為1，球副數目為2，連接兩個球副的連桿存在1個局部自由度，機構的自由度F=6×2-5-2×3-1=0，表明分支3的主動關節能完全控制動平臺繞u軸的轉動自由度。

綜合以上分析可知，分支1、2、3、4內的4個移動副能完全控制動平臺的4個自由度，驅動選取合適。

2 位置分析

位置分析的目的在于建立主動關節輸入參數和動平臺輸出位姿參數間的映射關系。分析的機構中4個移動副為主動關節，對應的長度為d1、d2、d3、d4，是輸入參數。動平臺的位置可由動坐標系原點p在定坐標系中的位置矢量p=(x，0，z)T表示，姿態可由旋轉變換矩陣R表示

R=R(y,α)R(u,β)=

(5)

式中R(y,α)——繞y軸轉動角α的旋轉矩陣

R(u,β)——繞u軸轉動角β的旋轉矩陣

R(y,α)、R(u,β)分別對應機構的2個轉動自由度。因此，動平臺的位姿可由x、z、α、β4個參數表示。

在定坐標系中，點Ai(i=1,2,3)的位置矢量可表示為

(6)

在動坐標系中，點Bi(i=1,2,3)的位置矢量可表示為

(7)

其中，右上標p表示參考的是動坐標系。

可通過坐標變換將點Bi(i=1,2,3)在定坐標系下的位置矢量求得。變換公式為

(8)

將式(5)、(7)代入式(8)中，可得

(9)

根據A1、A2、B1、B2的位置矢量，可以求得點C1、C2的位置矢量為

(10)

根據分支的結構，可以建立4個約束方程

(11)

將各點位置矢量代入式(11)，可得到4個方程為

(12)

(13)

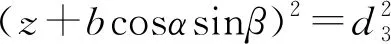
(14)

(15)

位置逆解是已知動平臺輸出參數x、z、α、β，求解輸入參數di(i=1,2,3,4)。可很容易地通過式(12)～(15)求得，注意di(i=1,2,3,4)為移動副長度，應取正值。位置正解是已知輸入參數di(i=1,2,3,4)，求解x、z、α、β，屬于方程求解問題。

3 奇異分析

并聯機構的工作空間內可能存在奇異位形，會導致機構剛度退化、失去控制等不良后果，應對奇異位形進行分析。奇異分析一般在速度雅可比矩陣的基礎上開展，將方程(12)～(15)對時間求導，得到速度方程，可整理為

(16)

其中

可以得到機構的雅可比矩陣J為

(17)

并聯機構的奇異位形可分為3類[19]：逆奇異、正奇異和混合奇異。

當矩陣JA的行列式值等于0，但矩陣JB的行列式值不為0時，機構處于逆奇異位形。根據矩陣JA的表達式可知，只有當某個移動副長度di=0時，JA的行列式值為0。但考慮到實際情況，這種條件無法滿足。因此，機構不存在逆奇異。

當矩陣JB的行列式值等于0，但矩陣JA的行列式值不為0時，機構處于正奇異位形。通過分析可以發現，機構有2種正奇異位形。

第1種正奇異位形發生在線段A3B3穿過線段B1B2時，如圖5所示。此時，動平臺繞u軸轉動自由度失去控制。

第2種正奇異位形是當d4取最大值，即到達峰頂。此時，d4變化可能會使得機構向兩個不同的方向運動(峰頂的兩側)，機構不具有確定的運動。

為直觀地展示機構奇異位形，設定機構的尺度參數如下：a=170 mm，b=66 mm，c=80 mm，令z=-220 mm，det(JB)=0，可得到機構的正奇異位形曲面如圖6所示。可以發現，機構的正奇異位形包含兩個曲面，分別對應兩種正奇異情況。

圖7為當β=0時，工作空間內d4分布情況。黑色曲線代表第2種正奇異位形。可以發現，黑色曲線與d4長度的峰值吻合，證實了奇異位形分析的正確性。

當矩陣JA和JB的行列式值都等于0時，機構發生混合奇異。由于JA的行列式值不可能為0，機構沒有混合奇異。

4 性能分析

4.1 剛度分析

當在并聯機構的動平臺上施加載荷后，由于機構的柔性，動平臺會偏離預定的位置，從而影響操作精度。剛度反映機構受力時抵抗彈性變形的能力，是評價并聯機構的一種重要性能指標。

本文考慮驅動的柔性，對機構進行剛度分析。根據虛功原理[20]，建立并聯機構平衡方程為

τTδq-FTδx=0

(18)

式中τ——驅動關節的力或力矩

δq——驅動關節對應的虛位移

F——動平臺受的力或力矩

δx——動平臺虛位移

驅動關節的虛位移與動平臺的虛位移滿足

δq=Jδx

(19)

將式(19)代入式(18)可得

F=JTτ

(20)

驅動關節力或力矩和虛位移間滿足

τ=χδq

(21)

式中χ——對角矩陣

其對角線上元素代表驅動關節的剛度。

將式(19)代入式(21)，將結果代入式(20)，可得

F=JTχJδx

(22)

因此，得到并聯機構的剛度矩陣為

K=JTχJ

(23)

考慮到雅可比矩陣含有動平臺的位姿參數，可知并聯機構的剛度會隨位姿變化。衡量剛度的指標包括剛度矩陣的條件數、特征值、對角線元素等[21]。在設計時通常希望機構的最小剛度大于一定的值以確保機構的精度[22]，因此選取剛度矩陣的最小特征值作為剛度評價指標。

由于本文機構具有移動和轉動混合自由度，雅可比矩陣J存在量綱不統一的問題，從而導致剛度矩陣缺乏物理意義。為解決這個問題，采用特征長度的方法[23-24]，在對應角速度的雅可比矩陣后兩列除以一個表示機構尺度的特征長度L來實現量綱的統一。選取點A1和A2間距離為特征長度。注意，剛度矩陣K中所用的J即是量綱統一后的雅可比矩陣。不失一般性，將所有驅動的剛度系數均設置為1×106N/mm，可以得到機構工作空間內剛度。圖8為x=0，z=-220 mm 時工作空間內機構的剛度指標K的分布情況。

由圖8可知，機構在α=0°時，剛度退化為零。對比圖6可以發現，此時機構處于奇異位形(圖8中的黑色虛線即代表奇異位形)，在鎖住所有的驅動后，動平臺仍有瞬時自由度。剛度分析與奇異分析結果吻合。

為消除工作空間內部奇異，提高機構的剛度性能，可以在機構中添加冗余驅動分支[25-26]。圖9為在原機構上添加了RPU結構的分支5，形成的冗余驅動并聯機構。注意，分支5和分支1共用末端的虎克鉸。由于分支5和分支1的位移流形相同，由李群理論可知，機構自由度沒有改變。

設計分支1和分支5中與基座相連轉動副的中心距離為440 mm，采用非冗余機構類似的分析方法，可以得到同樣條件下冗余驅動機構工作空間內剛度指標分布情況。圖10為x=0，z=-220 mm時冗余驅動機構的剛度指標分布情況。

對比圖8和圖10可以發現，在添加一個冗余驅動的分支后，機構工作空間中心區域的剛度性能得到了大幅提升，這是由于添加的冗余驅動分支消除了第2種正奇異位形。

4.2 工作空間分析

機構工作空間也是一項重要性能指標。冗余驅動機構由于增加了額外分支，其工作空間相較于非冗余機構勢必會減小。考慮機構的結構特點，設定分支1、2、3、5中移動副伸縮范圍為200～300 mm，而分支4中移動副伸縮范圍為150～250 mm，當z=-220 mm時，非冗余機構和冗余驅動機構的三維工作空間分別如圖11、12所示。

由圖11、12可以發現，添加冗余驅動分支后，機構的工作空間變小。對工作空間分層分析，令x=-40 mm，x=-20 mm，x=0，x=20 mm，x=40 mm，分別繪制非冗余機構和冗余驅動機構的二維工作空間，如圖13所示。可以發現在遠離x=0的區域，非冗余機構的轉動工作空間大于冗余驅動機構。在x=0附近的中心區域，冗余驅動機構和非冗余機構的轉動工作空間基本一致。

分析冗余驅動機構構型可知，當動平臺姿態保持水平時，隨著動平臺位置參數x從0開始負增長，分支1和分支5的長度變短，此時，如果動平臺饒y軸順時針轉動，分支5的長度將進一步壓縮，導致分支5中移動副行程更容易達到下限，限制了動平臺繞y軸順時針轉動的角度。另一方面，如果動平臺位置參數x從0開始正增長，分支1和分支5的長度變長，此時，動平臺繞y軸的逆時針轉動會使得分支5的長度進一步增加，導致分支5中移動副行程更容易達到上限，限制了動平臺繞y軸逆時針轉動的角度。當x=0時，由于對稱性，分支5對工作空間的約束與分支1相同，故此時冗余驅動機構的工作空間與非冗余機構一致。由圖13可知，相對于非冗余機構，當x小于0時，冗余驅動機構的工作空間在α的負方向變小；而當x大于0時，工作空間在α的正方向變小；當x=0時，工作空間沒有變化，這種變化規律與機構的構型特點吻合。

并聯機構的奇異位形會將工作空間分割為多個割裂的區域。圖13中白色虛線代表奇異位形，可以發現，在x=0附近，冗余驅動機構的非奇異工作空間比非冗余驅動機構更大。

5 尺度優化設計

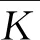
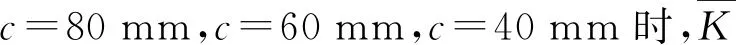
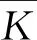
圖16為尺度優化后(b=78 mm，c=80 mm)機構的剛度指標分布。對比圖10可以發現，經過優化設計，冗余驅動機構的剛度性能得到了明顯提升。

6 結論

(1)提出了一種具有耦合分支的新型并聯機構，其動平臺能輸出兩個轉動運動和兩個移動運動。該機構配合一個移動工作臺可作為五軸機床的本體。

(2)基于雅可比矩陣分析了機構的奇異位形。該機構具有2種正奇異情況，會導致剛度退化，通過添加冗余驅動分支可有效提升機構的剛度性能。

(3)冗余驅動機構的性能與尺度相關，通過尺度優化設計可進一步提升機構工作空間內的剛度性能。