在幾何教學中滲透數學核心素養的探討

錢燦坤

一、精心準備，確定教學策略

1.借助實際活動，加強數學思想方法的滲透

在教學中盡可能地讓學生體會蘊涵在知識內的數學思想方法，滲透猜想與驗證、轉化與歸納的數學思想。教學過程中，首先，在算出直角三角形的內角和是180°后，猜想銳角三角形和鈍角三角形的內角和，再通過實踐操作驗證。其次，在驗證完銳角三角形、鈍角三角形的內角和都是180°時，又用到了歸納整理的數學思想方法，從而推出所有的三角形的內角和都是180°。最后，經歷剪、拼、折等一系列的操作活動，將三角形的三個內角轉化成一個平角，從而得出三角形的內角和是180°，向學生滲透轉化的思想方法。

2.合理安排教學環節，組織學生在感知、猜想、驗證和歸納的過程中學習三角形的內角和

主要有以下四個層次：

第一層次是明確概念：學生通過找出各種三角形的內角，明確“內角和”的概念，即“三角形三個內角度數的和就是三角形的內角和。”

第二層次是初步感知：學生已經了解了三角板上各個角的度數，為了避免學生猜測的盲目性，教師引導學生回憶并計算，發現三角板中的三個內角的和是180°，即直角三角形的內角和是180°，為學生進一步的猜想奠定了理論基礎。

第三層次是理論猜想：是不是所有三角形的內角和都是180°呢？這個問題的拋出為后面的猜測和驗證作好鋪墊，引發學生思考，激發學生的探究欲望。

第四層次是操作驗證：在這一環節采用“先扶后放”的原則，沒有完全放手給學生，而是通過實際測量計算，使學生的猜想得以證實，三角形的內角和是180°。學生分小組對大小不一的三角形進行驗證，通過剪、拼、折等一系列的操作活動，將三角形的三個內角轉化成一個平角，從而得出“三角形的內角和是180°”這一結論。

二、實踐探討，踐行教學環節

（一）問題導入，引發思考

提問：我們前面學習和了解了三角形的相關知識，請大家說說三角形按角分，可以分成哪幾類？

提問：你能畫出含有兩個直角的三角形嗎？為什么會畫不出來？

（二）探究三角形內角和

1.猜一猜：有大小不同的三角形讓學生猜這些三角形的三個內角和都是一樣嗎？

2.量一量：分別量出銳角三角形、直角三角形、鈍角三角形3個內角的度數，并計算出它的內角和。你從中發現了什么？

3.拼一拼：將自己準備好的三角形的三個角撕下來，拼在一起，你又發現了什么？

4.看一看：教師演示折拼過程，學生觀察。你又發現了什么？

（三）課堂練習，鞏固新知

1.計算三角形中∠3的度數，并判斷它是什么樣的三角形。

（1）∠1=20°，∠2=70°，∠3=（? ? ），是（? ? ）三角形。

（2）∠1=55°，∠2=45°，∠3=（? ? ），是（? ? ）三角形。

2.判斷。

（1）直角三角形的兩個銳角的和是90°。（? ）

（2）一個等腰三角形的底角可能是鈍角。（? ）

3.紅領巾是一個等腰三角形，如果它的頂角是120°，求它的另外兩個角的度數。

4.回顧課前的疑問：為什么畫不出含有兩個直角的三角形？

三、教學反思，明確核心素養的落實

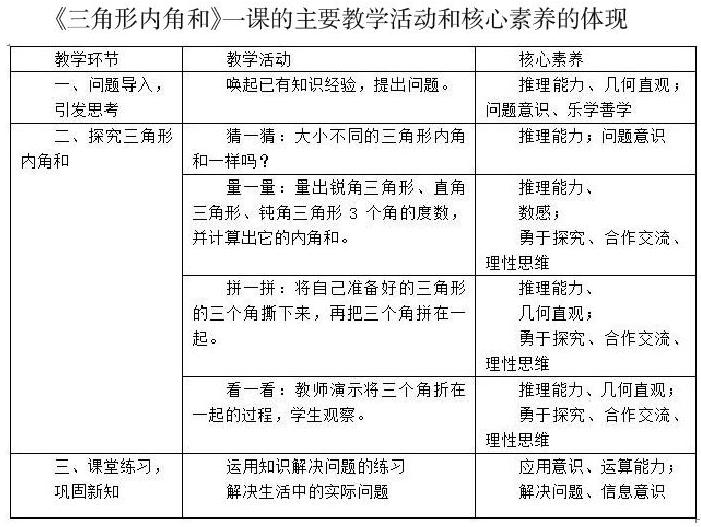
下面表格是對主要環節中的教學活動體現的核心素養做的歸納。

《三角形內角和》一課的主要教學活動和核心素養的體現

在《三角形內角和》一課里，我十分重視引導學生對幾何圖形的探究和理解，學生在學習過程中膽猜想、自主探索，圍繞著主問題展開了積極的自我探索和合作研究，數學核心素養在期間得到較高水平的培養。學生在動手操作、積極探索的活動過程中掌握知識，積累數學活動經驗，發展空間思維和推理能力等數學核心素養，也能夠讓勇于探究和理性思維等學生發展的核心素養落到實處。

從本節課的案例分析可以得出，一節完整的課堂教學所體現的核心素養是多元的，同時也是有所側重的，例如有數學核心素養、推理能力、抽象能力、模型思想、運算能力、幾何直觀、數感和應用意識等。學生發展核心素養在《三角形內角和》中的體現有學生發展核心素養、理性思維、勇于探究、問題意識、信息意識、合作能力、樂學善學和創新意識等。