基于位置差的特征序列挖掘快速算法*

潘向榮，王 婷

(1.中國西南電子技術研究所，成都 610036；2.電子科技大學 通信抗干擾技術國家級重點實驗室，成都 611730)

0 引 言

公開通信協議的數據幀結構是確定并易知的，但在某些特殊場景尤其是軍事應用環境中，為提高數據傳輸的安全性，通信方通常不會采用公開的通信協議，而是采用專用的通信協議進行數據傳輸，這些專用通信協議通常是不公開的。因此，在電子對抗中，數據幀格式對非合作接收方而言是未知的，從偵查截獲的通信比特流中識別出幀結構進而識別通信協議，將協議幀頭與數據載荷區分開來，從而進一步對截獲的數據載荷進行破譯等分析，對分析網絡拓撲結構、識別信息流目標以及網絡抗干擾通信具有重要意義。

目前，國內外對數據鏈路層未知協議的識別領域的研究進展較為緩慢[1-10]。“未知協議”是指具有一定固定幀頭格式的未公開協議。比特流未知協議識別的一般思路是：基于統計理論挖掘出比特流的特征序列等協議特征，根據一般通信協議的基本特征來進一步確定比特流的幀頭位置，進而分析出比特流的幀格式。對于未知的通信協議，分析者并沒有可以參考的特征序列，必須通過枚舉和統計方法來篩選、比對等步驟挖掘出特征序列。從比特流中如何快速、準確的分析出特征序列是識別未知通信協議的關鍵。

一般說來，未知通信協議識別包括數據預處理、頻繁序列提取(統計與篩選)、特征序列挖掘和特征序列關聯分析4個主要步驟。

數據預處理是指將獲取的數據轉換為01比特流，頻繁序列提取是指對模式序列進行準確計數，并通過預設閾值，根據一定的篩選規則篩選出頻繁序列，然后通過拼接等手段獲得較長的頻繁序列，從而得到候選特征序列集合。最后，應用關聯規則挖掘技術對候選特征序列進行關聯規則挖掘，由此確定未知通信協議的特征序列和可能的協議幀結構。

文獻[2]采用AC(Aho-Corasick)統計算法完成頻繁序列的提取(包括統計與篩選)。該算法基于二叉樹來實現對模式序列出現位置的存儲。在對模式序列進行統計計數時需要遍歷整棵二叉樹節點，其遍歷代價很大。本文在分析出AC快速統計算法[2]的這一缺陷后，改進了模式序列的統計方式，采用數組代替二叉樹存儲比特流中模式序列的位置信息，并構造了使得數組下標值與二叉樹節點值保持一致的關系式，有效降低了對模式序列進行計數及篩選的時間復雜度。進一步，本文將存儲各頻繁序列位置信息的數組依次連接成一個長數組，并按頻繁序列出現位置的先后順序重新排列該數組元素，進而改進了基于位置差的特征序列挖掘算法。與原算法相比，改進算法大幅度減少了算法迭代次數，將頻繁序列拼接時間減少了至少一個數量級，快速挖掘出了比特流中的特征序列。

1 相關概念

設有長度為n的隨機比特流序列S，對于S中的任意一個模式序列P，不妨給出如下定義：

定義1 假定P中包括m個比特，則稱P的長度為m。

定義2 假定P為長度m的模式序列，Q為長度q的模式序列，q≤m，且P的1～q位均與Q的對應位置比特相同，則稱Q是P的子序列，P是Q的父序列。

定義3 假定S中共有r個長為m的模式序列，其中模式序列P出現了k次，則P的支持度supp(P)為k/r。

定義4 假定supp(P)不小于用戶規定的最小支持度，那么P為頻繁序列；反之，為非頻繁序列。

2 基于位置差的特征序列挖掘快速算法

2.1 AC快速統計算法的改進

AC算法是于1975年由貝爾實驗室的Aho和Corasick兩位研究人員提出的一種多模式匹配算法，該算法是模式匹配領域的經典算法之一。金陵等人[2]提出的AC快速統計算法是基于AC算法的一種改進，該算法將二叉樹存儲結構改為使用數組結構進行比特流中模式序列的存儲，可以實現對比特流中出現的所有模式序列統計完全。

顯然，比特流序列的元素取值為0或1。因此，長為m的模式序列P有且僅有兩個長為m+1的父序列。窮舉長度取值為[1，m]的所有模式序列可構成一棵完全二叉樹。圖1表示由長度區間為[1，4]b的所有模式序列構成的二叉樹。

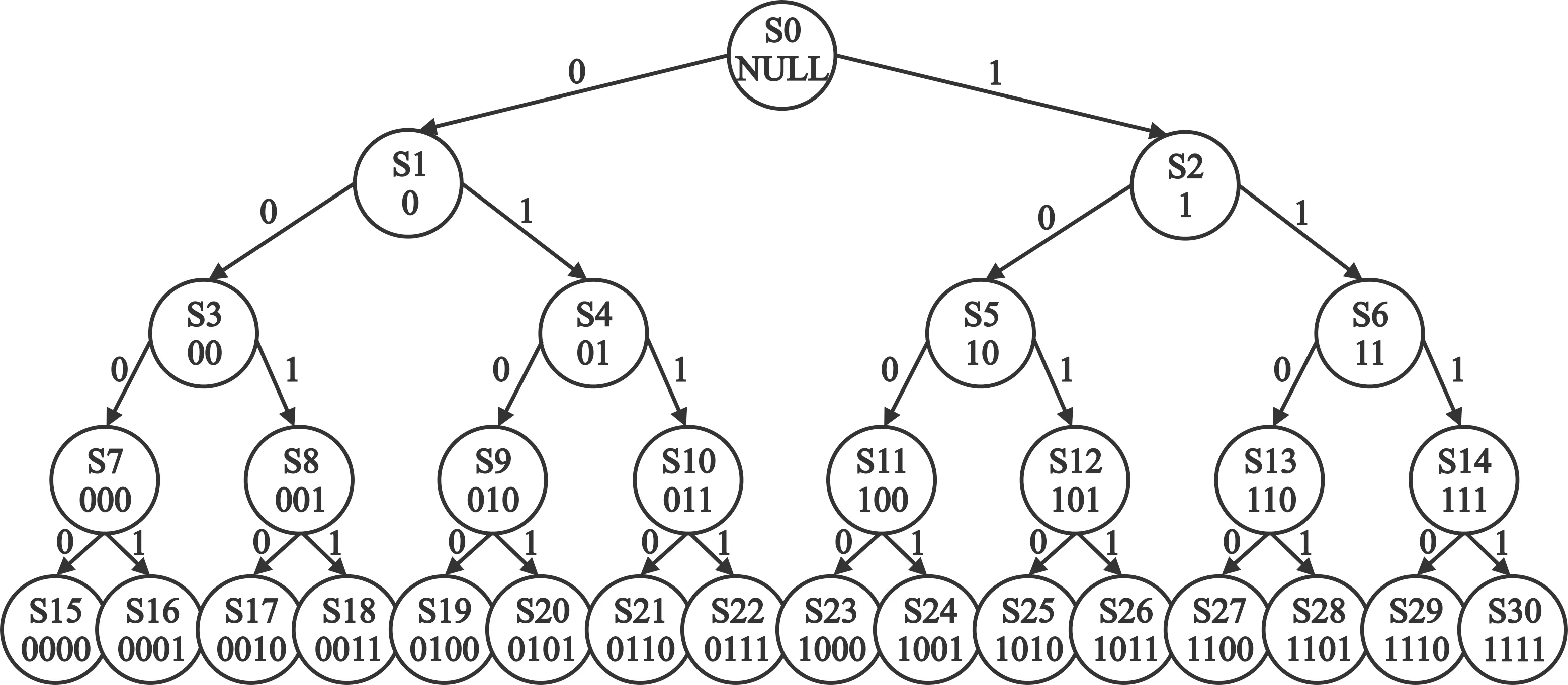
圖1 長為1～4 b的模式序列所構成的完全二叉樹

AC快速統計算法基于二叉樹來實現對模式序列出現位置的存儲。在對模式序列進行計數時需要遍歷整棵二叉樹節點，其遍歷代價很大。

經過對二叉樹存儲結構和相關存儲結構特點的深入分析，采用數組代替二叉樹存儲比特流中模式序列的位置信息，并構造了使得數組下標值與二叉樹節點值相等的關系式，基于此給出了一種復雜度更低的模式序列統計算法。該算法的創新之處在于，通過對所截獲的比特流的存儲結構的修改，使得在對模式序列的計數過程中極大降低了對模式序列的掃描次數，進而極大減少了統計過程中所需的計算時間和存儲空間。

本文對文獻[2]中的AC快速統計算法進行了改進，通過分析各模式序列與數組下標之間的邏輯關系，構造了使得存儲模式序列對應的數組下標值與二叉樹節點值相等的表達式，具體為

Index= dec(x)+2Length(x)-1

(1)

式中：x表示模式序列，dec(x)表示x對應的十進制數，Length(x)表示x的長度，Index表示x在存儲其位置信息的數組中的下標值。

根據式(1)，所有的模式序列均與存儲其位置的數組的下標值對應。將圖1中的二叉樹采用式(1)列出模式序列與存儲其位置的數組的下標號之間的對應關系,如表1所示。

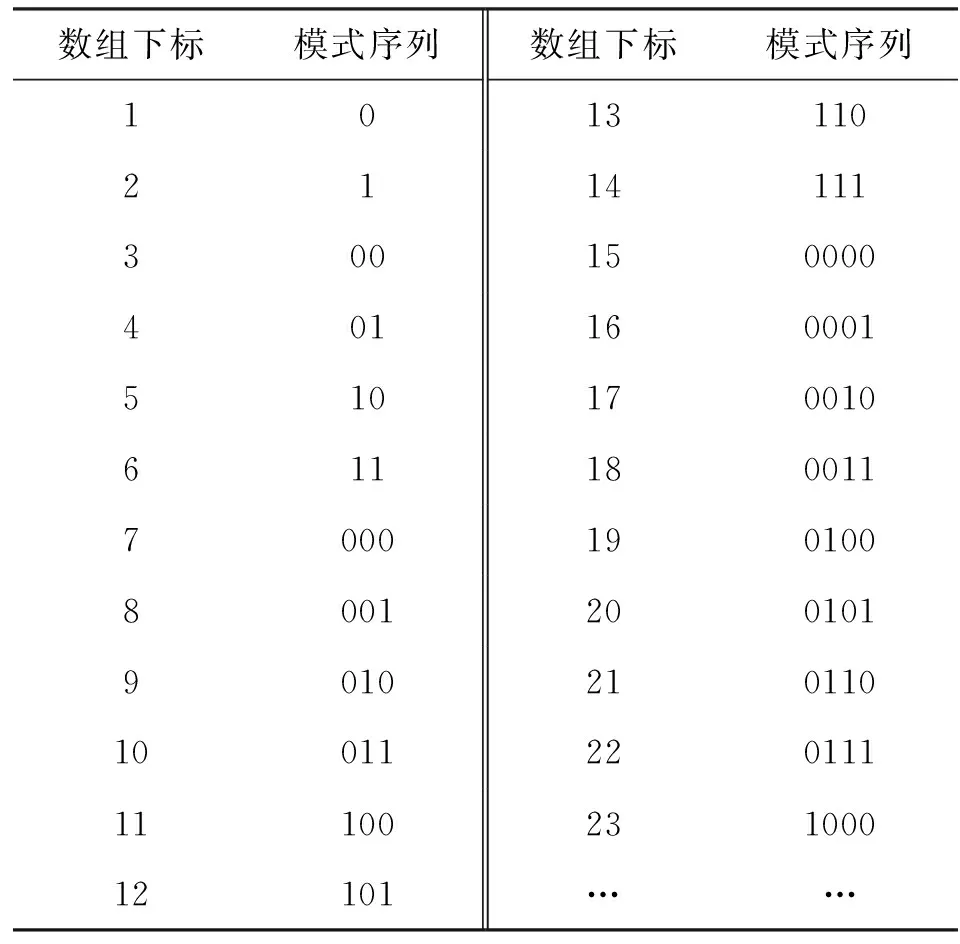
表1 模式序列與數組下標的映射關系

將表1和圖1進行比較，不難發現如下事實：比特流中各模式序列在數組中的下標值與這些模式序列在二叉樹中的節點值完全對應。這一事實可以更為直觀地比較模式序列在二叉樹結構和數組結構下的存儲特征。

2.2 基于閾值的頻繁序列篩選

在無任何先驗信息情況下，假設對長度為m的模式序列進行計數，不失一般性，假定0和1等概率出現在每一個比特位置上，那么，長為m的模式序列的種數為2m。不妨假定待識別的比特流S的隨機性良好，那么每種長為m的模式序列的出現概率均為1/2m。根據支持度的定義，則長度為m的模式序列的平均支持度等于1/2m。不難得知，長為n的比特流S中存在(n-m+1)個長度為m的模式序列。因此，長為m的模式序列出現的平均次數為(n-m+1)/2m。

通常，篩選閾值Th被設置為

(2)

式中：參數α的作用為調節閾值大小，n表示序列S的長度，m表示模式序列的長度。

在所有的模式序列的計數和閾值設置完成以后，根據對比模式序列的計數值與篩選閾值的大小以及篩選規則，可將所有的模式序列劃分為頻繁序列和非頻繁序列，所有被列為頻繁序列的模式序列構成頻繁序列集合。

2.3 基于位置差的長序列拼接改進算法

一般來講，子序列的出現次數均大于其父序列的出現次數。因此，子序列被篩選為頻繁序列的機會大于其父序列。換句話說，頻繁序列集合中更多的是長度較短的模式序列。但在實際協議中，也會存在長度較大的特征序列。序列拼接是獲得較長模式序列的一種主要方法之一，即將滿足一定要求的較短的頻繁序列通過拼接的方式獲得較長的模式序列。

文獻[2]介紹了一種基于位置差的長序列拼接方案，但該方案在對短序列進行拼接的過程中需要大量的重復迭代操作。經分析，該序列拼接算法存在如下三個不足：第一，復雜度高；第二，存在特征序列挖掘誤差；第三，序列重疊度高。本文從這些分析結果出發，對基于位置差的長序列拼接算法進行了改進。改進算法充分利用了各頻繁序列在比特流中出現位置的先后順序這一信息，在對頻繁序列集合進行存儲表示時，改進算法按照各頻繁序列的出現位置來進行存儲。這一改進大幅簡化了拼接過程中的迭代次數。

在文獻[2]中，將同種頻繁序列出現的多個位置信息存儲在同一個數組中，如表2所示。

表2 頻繁序列與其出現位置對應表

在表2中，xi(i=1,2,…,N)表示第i種頻繁序列，而pi,j表示第i種頻繁序列的第j個出現位置。這種頻繁序列與表示其出現次數位置的數組之間的對應關系，不能準確刻畫出這兩個頻繁序列間的出現位置的先后順序。例如，無法直接判斷出模式序列p1,1和p2,1的大小關系，只能分別將這兩個模式序列的數值取出并進行比較才能做出判定。這直接導致了該拼接算法的復雜度較高。

基于對AC快速統計算法的不足的分析，本文提出了改進算法。改進算法在基于表2所示的存儲方式上，將各模式序列對應的所有數組依次首尾連接成一個數組P，如表3所示。顯然，此時頻繁序列出現位置的總數，即為頻繁序列集合的元素個數。

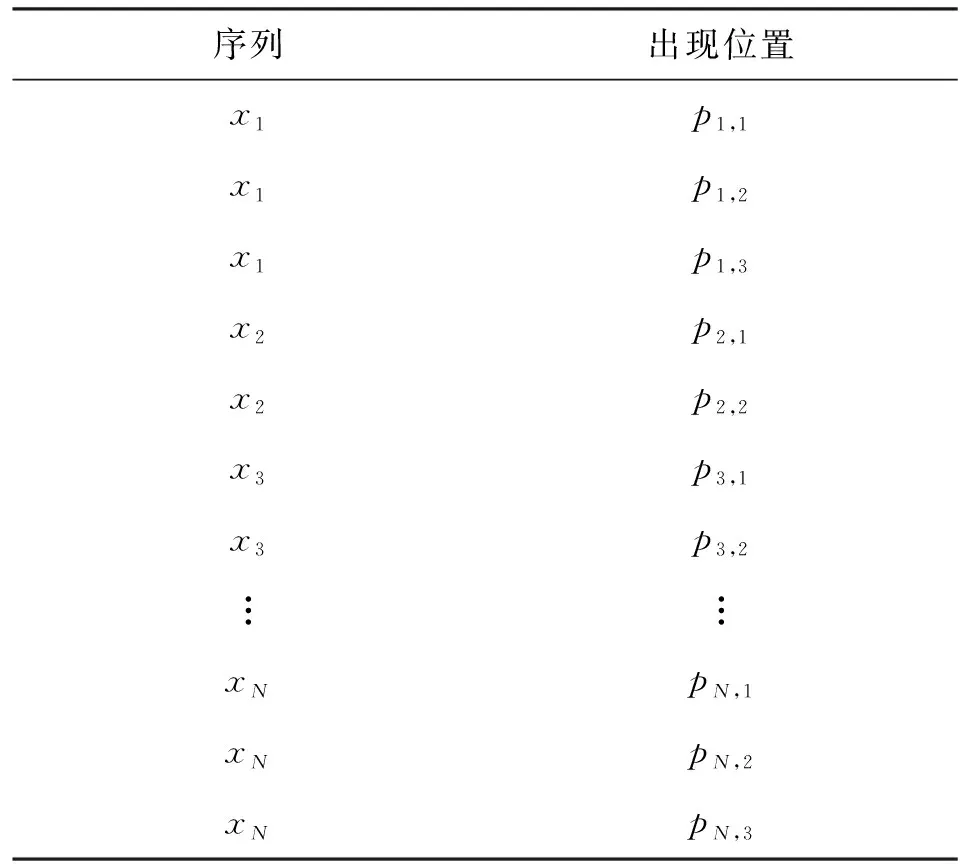
表3 頻繁序列與其出現位置一一對應表

進一步，將數組P中的元素按照相應頻繁序列出現位置的先后順序從左到右進行排序，然后，進行基于位置差的長序列拼接，其拼接算法流程如圖2所示。

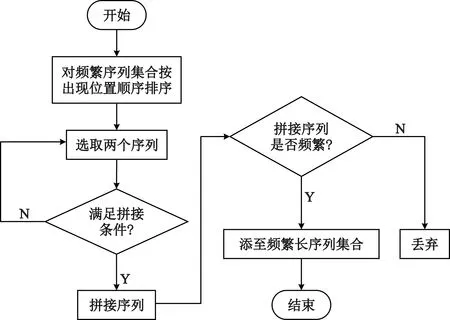
圖2 基于位置差的長序列拼接算法流程

將滿足如下拼接條件的兩條頻繁序列xi和xj進行拼接，然后對拼接后的長序列進行篩選，判斷其是否為頻繁序列。拼接條件仍然為[2]

pos(xj)- pos(xi)=Length(xi) 。

(3)

式中：pos(xi)和pos(xj)分別表示序列xi和xj在輸入比特流中的出現位置。這里需要指出的是，因為改進算法的拼接條件與原算法一致，因此，拼接而成的長序列的輸出結果與原算法也完全相同。

基于位置差的長序列拼接改進算法的偽代碼如下：

1 初始化XS=?,P=?;

2 fori=1 to length(Xs) do

6 end for

7 end for

8 對P進行由小到大的排序，并對X進行對應的元素交換；

9 初始化i←1,j←i+1,Xtemp=?;

10 while true do

11 ifP[j]-P[i]=length(X[i])then

12xnew←splice(X[i],X[j]);

13 ifxnex?Xtempthen

14Xtemp←Xtemp∪xnew,pos(xnew)←pos(xnew)∪i;

15 else

16 pos(xnew)←pos(xnew)∪i;

17 end if

18i←i+1,j←j+1;

19 else ifP[j]-P[i]>length(X[i])then

20i←i+1;

21 else

22j←j+1

23 end if

24 if j=length(X)+1 then

25 ifXtemp=? then

26 break;

27 else

28 篩選Xtemp中滿足閾值的頻繁序列，并將篩選出的序列集合展開為Xsel以及其出現位置集合Psel;

29 ifXsel=? then

30 break;

31 end if

32 對Psel進行排序，Xsel也對應進行排序；

33 初始化k←1,l←1;

34 while true do

35 ifP[k]=Psel[l] then

36X[k]←Xsel[l],k←k+1,l←l+1;

37 else

38k←k+1;

39 end if

40 ifl=length(Psel)+1 then

3 算法分析及算法有效性驗證

與原算法[2]相比，本文提出的改進算法采用一個數組來存儲所有頻繁序列的位置信息，且數組元素依照對應頻繁序列出現位置的先后順序從左到右依次排列，該存儲方式極大減少了算法的迭代次數。在原算法[2]中，需要掃描所有可能的位置差來判斷拼接條件(式(3))是否滿足，極大增加了算法中的迭代操作，導致原算法的復雜度較高。改進算法在拼接過程中只需要遍歷頻繁序列集合一次，極大減少了迭代地進行拼接條件的判斷操作，使得改進算法的復雜性大大低于原算法。

為驗證算法的有效性，我們采用Visual C++開發平臺編寫程序實現算法，使用Wireshark抓包軟件截取數據包完成了算法性能有效性測試實驗。測試環境為Windows 7操作系統，Intel?CoreTMi5 7400處理器，CPU主頻3 GHz。

測試實驗方案的步驟如下：

Step1 使用Wireshark抓包軟件截取ARP包(200幀以上)進行測試，以包含100幀ARP協議幀的比特流作為實驗數據。

Step2 設置5組篩選閾值，分別為0.5、1.0、1.5、2.0和2.5。

Step3 對Step 1得到的實驗數據分別采用原算法[2]和本文的改進算法完成對實驗數據的比特流分析。

Step4 對比兩種算法下的時間復雜度。

表4給出了在不同閾值下上述兩種長序列拼接算法的仿真運行時間。

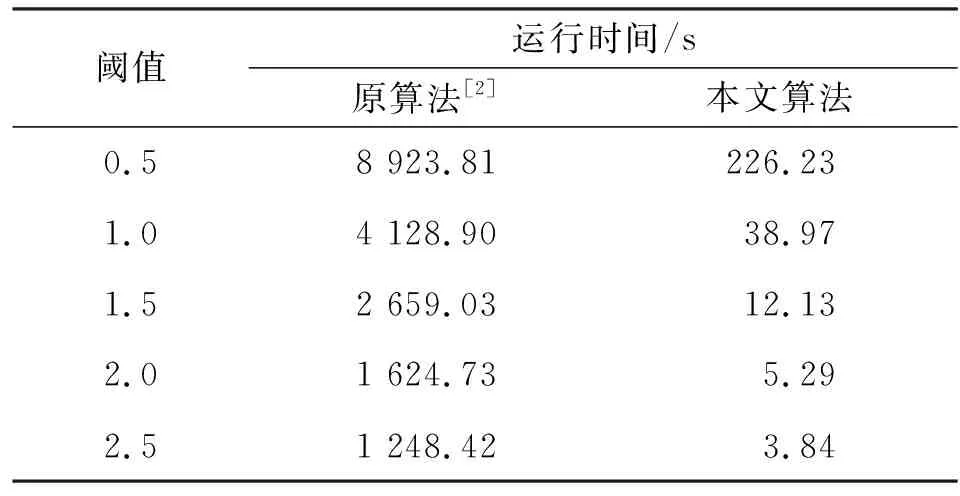
表4 不同閾值系數下兩種序列拼接算法的運行時間

從表4中的仿真數據可以得到以下結論:第一，隨著篩選閾值從0.5到2.5以0.5為步長逐漸增大，兩種拼接算法的計算時間均逐漸減少；第二，改進算法的時間復雜度遠低于原算法，表明對頻繁序列出現位置進行排序后再進行拼接的方案極大降低了拼接算法的時間復雜度，驗證了改進算法的有效性。圖3形象地展示了兩種算法的時間性能對比。

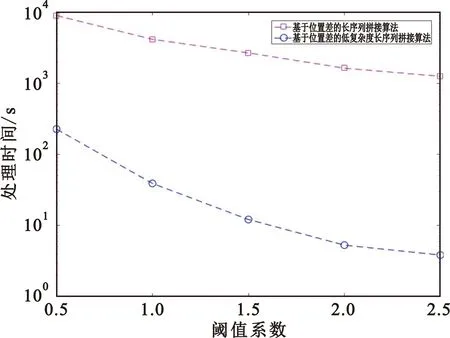
圖3 兩種序列拼接算法的時間復雜度比較

4 結 論

鏈路層中基于比特流的幀結構分析是進一步獲取情報信息的關鍵環節。金陵等人[2]提出的基于位置差的長序列拼接算法是面向比特流未知協議識別的主要算法。本文在深入研究該算法基礎上，提出了基于位置差的特征序列挖掘改進算法。改進算法采用數組來替代原算法中的二叉樹來存儲頻繁序列的出現位置信息，且數組元素依照對應頻繁序列出現位置的先后順序從左到右依次排列，這種存儲方式極大減少了算法的迭代次數。最后，使用Wireshark截取ARP包完成了算法的有效性測試。仿真結果表明，與原算法相比，本文的改進算法大幅度減少了算法迭代次數，將頻繁序列拼接時間減少了至少一個數量級，快速挖掘出了比特流中的特征序列，為進一步挖掘比特流的幀內結構奠定了基礎。