基于壓縮感知的室內多目標無線定位算法*
任 進,姬麗彬
(北方工業大學 信息學院,北京 100144)
0 引 言
自21世紀以來,隨著無線通信和信號處理技術的不斷進步,無線傳感器網絡(Wireless Sensor Network,WSN)[1]作為無線傳感技術的重要領域,正處在一個高速發展的階段。然而,節點能量受限是WSN技術發展與應用所面臨的重要挑戰,因此,研究如何保證低功耗的情況下對目標節點進行高精度的定位成為一個熱點問題。
近年來,對于如何優化WSN網絡中定位算法,國內外學者進行了很多研究。已有研究人員將壓縮感知(Compressed Sensing,CS)[2]技術與WSN相結合,利用 CS 技術降低信號的采集、傳輸、融合的能量消耗,同時實現網絡的定位,且取得了相應的成果。文獻[3-7]將機器學習運用于無線定位中:Ji等人[3]利用二元蜂群算法與壓縮感知結合進行定位,具有一定的智能性;李依純[4]利用提出的鄰域加強的二分 K-means 區域劃分算法,在離線階段對指紋庫區域進行聚類劃分,通過提出的改進的CS定位算法獲得定位坐標;Zhao等人[5]提出一種結合貝葉斯壓縮感知理論和離線指紋數據庫的構建方法,利用Co-Forest算法訓練的隨機森林分類器的決策結果以及多數原則獲得定位結果,為用戶完成實時定位;Zhang等人[6]提出一種基于信號到達相位差(Phase Difference of Arrival,PDOA)和接收信號強度(Received Signal Strength,RSS)的人工神經網絡(Artificial Neural Network,ANN)方案;劉夏等人[7]提出了一種利用模糊C均值聚類算法和模擬退火自適應遺傳算法去優化徑向基函數神經網絡的室內定位算法,顯著提高了傳統的徑向基函數神經網絡定位精度。文獻[8-9]通過處理節點接收信號強度進行優化:Khan等人[8]將多個待定位節點的RSS值進行疊加,再將壓縮的數據傳輸給信標節點,減少了流量開銷;Yu等人[9]利用多個待定位節點接收到的信號強度差(Received Signal Strength Difference,RSSD)代替傳統的RSS,提出一種基于接收信號強度差和壓縮感知的融合方法,減小終端異質性帶來的影響。文獻[10-11]則通過改進各類匹配追蹤(Matching Pursuit,MP)方法提高定位精度:Wu等人[10]提出利用階段式正交匹配追蹤算法(Stagewise Orthogonal Matching Pursuit,StOMP)提高運算速度,但造成了穩定性的下降;Li等人[11]將基于Voronoi圖的貪婪匹配追蹤(Greedy Matching Pursuit,GMP)方法用于在局部分區中搜索候選網格,大大減少了時間復雜度。
本文同時考慮低功耗和高性能的要求,提出了一種改進的基于貝葉斯壓縮感知(Bayesian Compressive Sensing,BCS)[12]的室內多目標定位算法。實驗仿真結果表明,與傳統的多目標定位算法相比,本文算法在網絡模型中估計出的未知節點位置和最終未知節點位置更為相近,定位效果有了顯著提高,同時大大減少了系統的通信量。
1 貝葉斯壓縮感知理論
BCS算法由壓縮感知理論和稀疏貝葉斯學習(Sparse Bayesian Learning,SBL)[13]結合所得,它通過符合某種先驗分布的隨機向量,計算出信號的先驗概率進而確定先驗分布;然后根據樣本信息,運用貝葉斯框架,計算最大后驗概率分布,得出信號的均值和方差,均值即為原信號恢復的估計值。
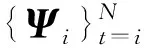
(1)
y實際上就是信號X在觀測矩陣Φ下的線性投影。
y=ΦX=ΦΨS=ΘS。
(2)
由于實際情況中存在噪聲的情況,所以公式(2)可進一步表示為
y=ΦX+n=ΘS+n。
(3)
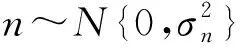
(4)
廣泛應用的稀疏先驗是拉普拉斯密度函數,然而,拉普拉斯密度函數的主要缺點是它無法共軛。 因此,我們考慮一個零均值的高斯先驗如下:
(5)
式中:α是N個獨立超參數的逆方差,即高斯先驗分布的精度。
假設α已知,我們的目的是估計參數S和σ2。那么給定α和y,將條件分布(4)與公式(5)中的先驗分布結合,通過貝葉斯準則來描述S后驗條件概率并使其最大化,這樣就得到了
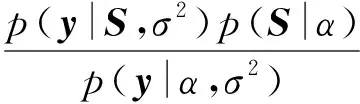
(6)
式中:S的后驗概率分布滿足均值為μ、協方差為Ω的多變量高斯分布,即
μ=σ-2ΩΘTy,
(7)
Ω=(Λ+σ-2ΘTΘ)-1。
(8)
式中:Λ~diag{α1,α2,…,αN} 。因此,觀測值y的后驗密度函數是一個具有均值E[y]=Θμ和協方差Cov[y]=ΘΩΘT的多變量正態分布。
貝葉斯壓縮感知重構算法的解釋如下:
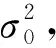
Step2 由于yl和Θ已知,使用公式(7)和(8)計算yl的均值μ和協方差Ω。

(9)
式中:μi是由式(7)所得的第i個后驗平均權重。定義γi=1-αiΩii,Ωi1是式(8)中的對角線元素。對于噪聲方差σ2,
(10)
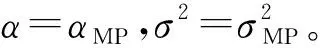
2 室內多目標定位的算法設計
室內多目標定位的過程如圖1所示。
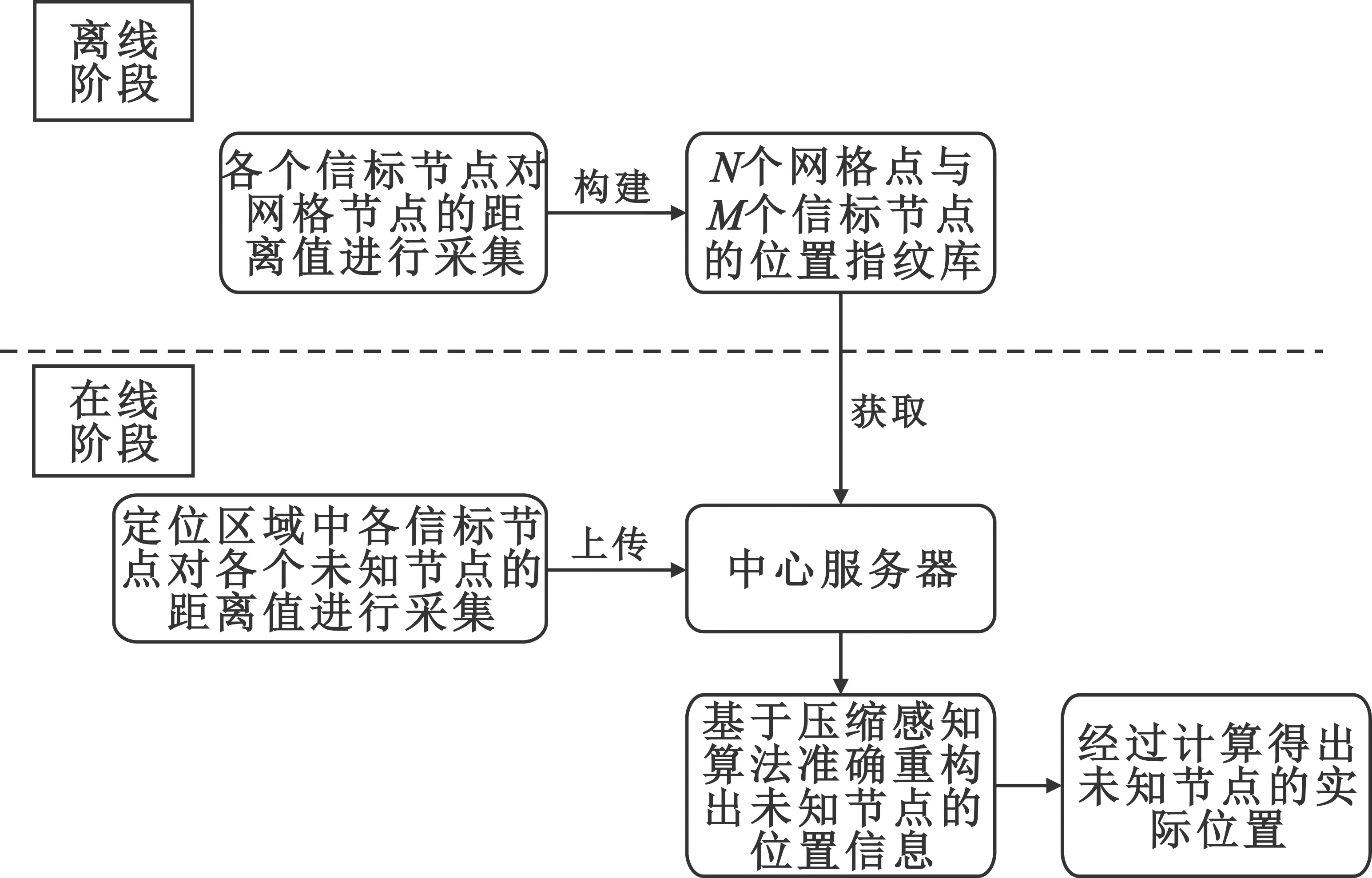
圖1 室內定位算法的流程示意圖
這一過程主要包含兩個階段,即離線階段和在線階段。
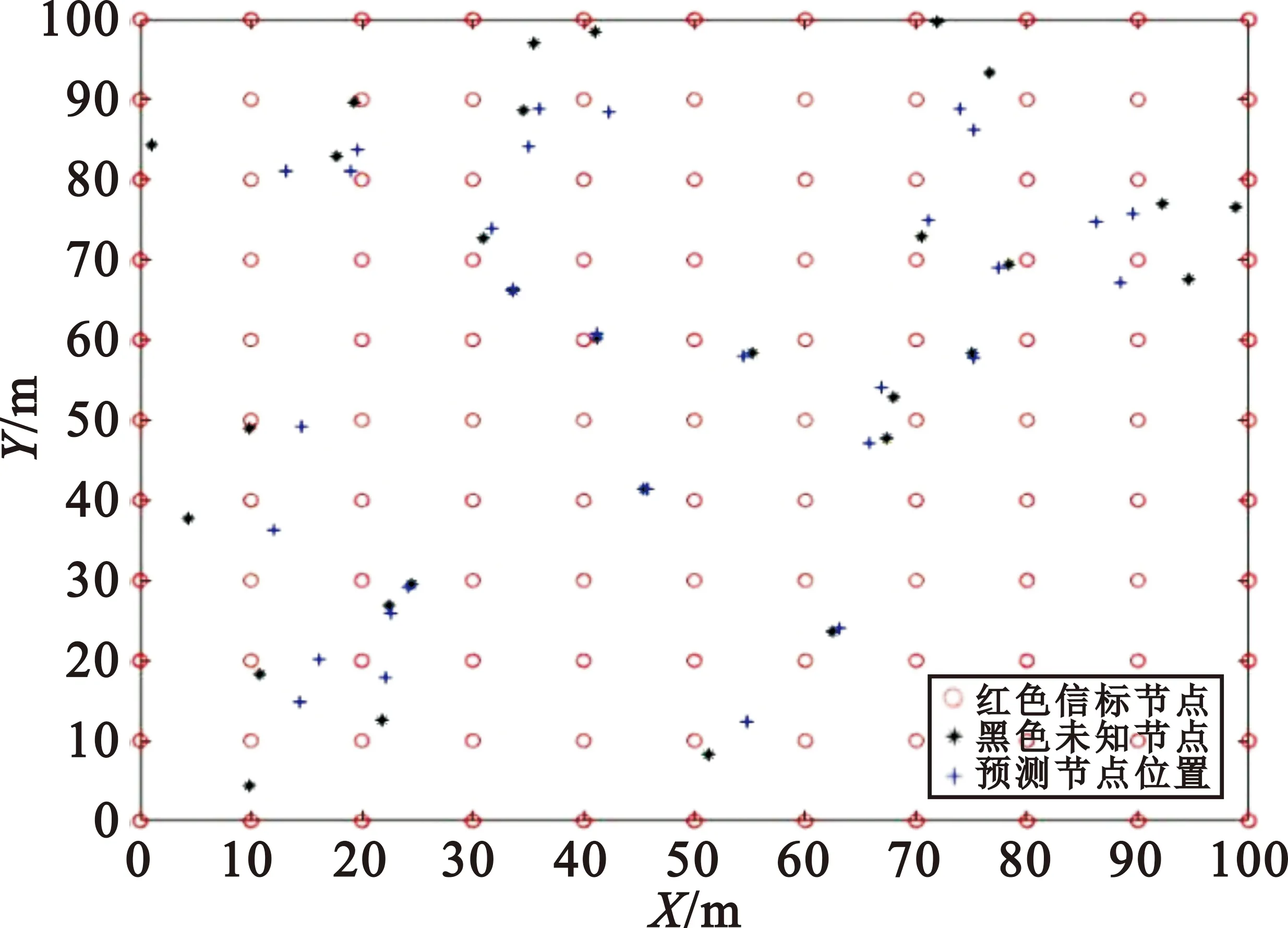
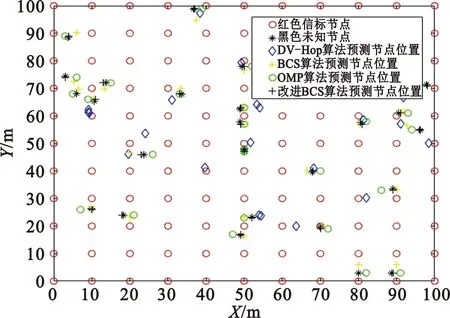
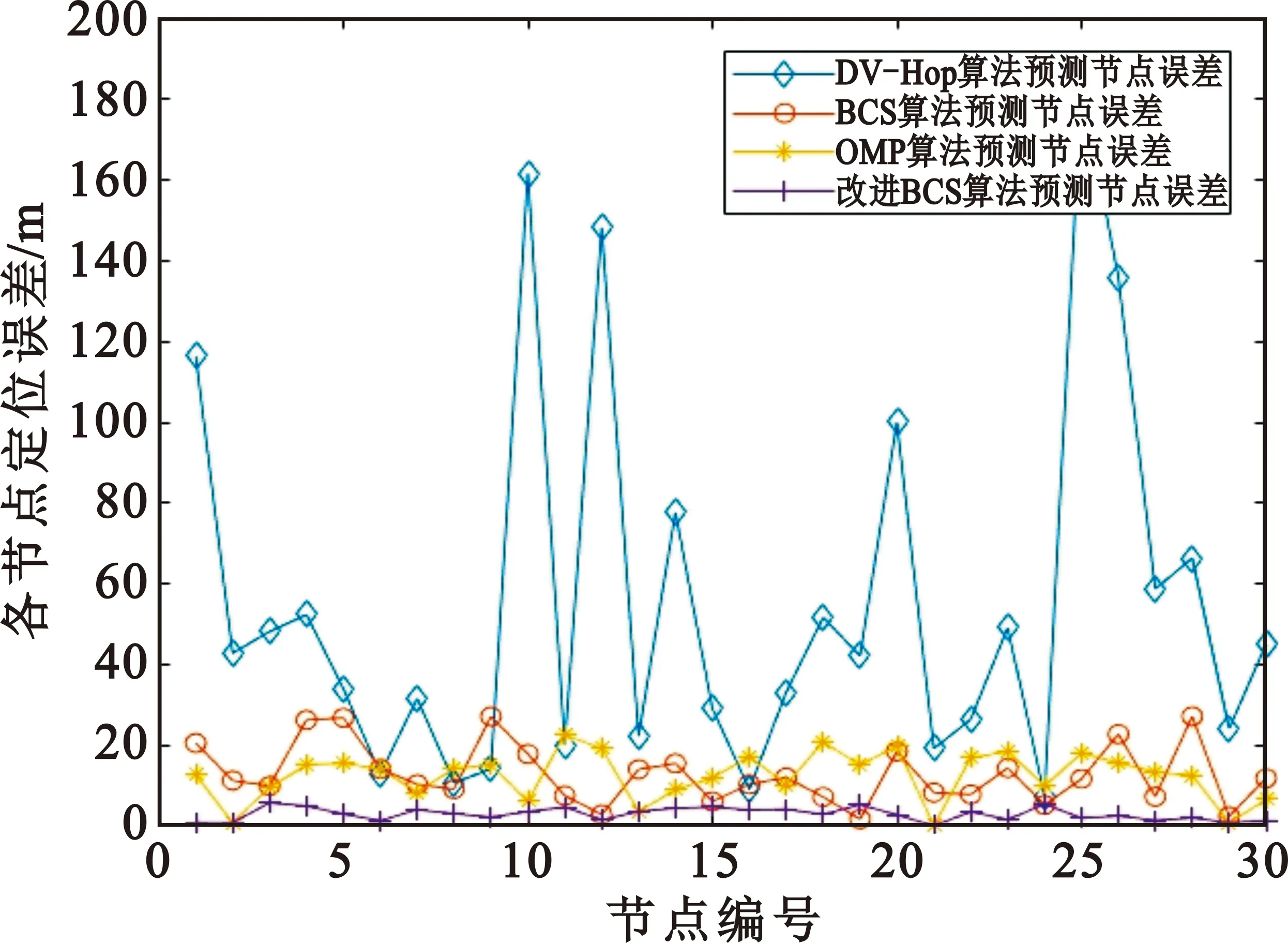
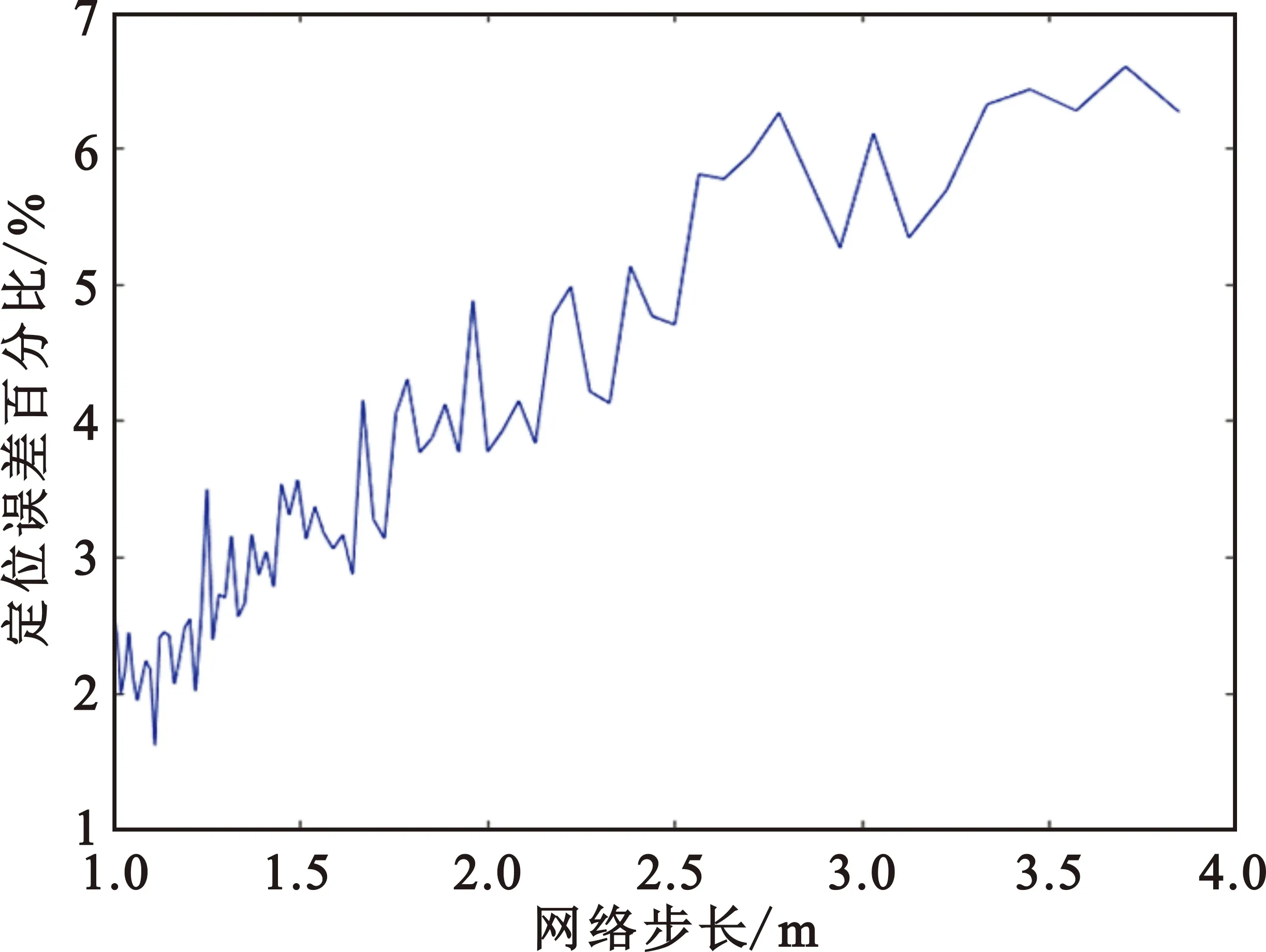
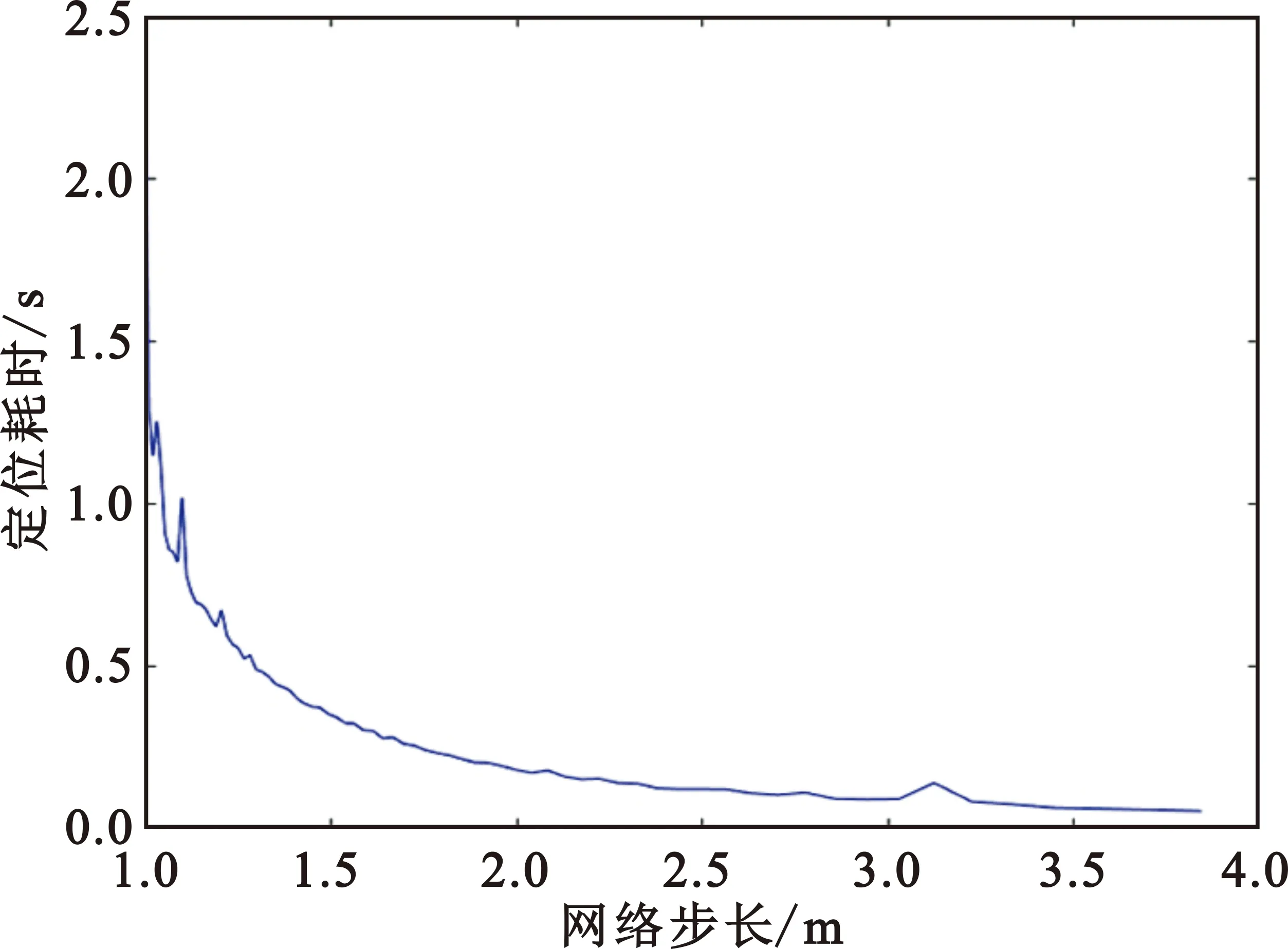
(1)處于離線階段時,無線接入點對定位區域內的每個網格節點的坐標位置進行記錄從而構建出該區域的位置指紋庫。首先,將被監測區域均勻劃分為N個網格,對網格按照一定的順序進行編號,本文按自左往右的順序編號,即N為網格的編號;將信標節點自上往下進行編號,M即表示區域中信標節點的編號。M個信標節點采集信息后構建的位置指紋庫Φ∈RM×N(M< (11) (2)處于在線階段即定位階段時,通過被監測區域信標節點對位置節點距離信息進行采集,并將這一測量值矩陣y上傳到中心服務器,中心服務器通過稀疏矩陣Ψ將上傳的這一系列數據進行隨機亞采樣和信號重構。由此,經過一系列的轉換將多目標定位問題轉換為稀疏信號重構的問題。同時,考慮到實際定位區域存在噪聲,則上述過程可以通過公式表示為 (12) 最后,利用壓縮采樣所得的測量值矩陣y,離線階段所構建出的位置指紋庫Φ和稀疏變換矩陣Ψ,通過以貝葉斯壓縮感知算法為基礎的定位算法進行最大似然估計,進而計算出稀疏信號位置向量S,查找信號中最大值的位序,將其對應到位置指紋庫中,即可精確計算出未知節點的位置坐標,有效實現定位的目的。 因此,本文的目的就是設計更加合理的稀疏變換基和觀測矩陣,在實現CS的兩個前提條件即稀疏性(sparsity)、不相關性(incoherence)的基礎上,實現更低的功耗和誤差。 由于室內環境中未知節點數量K遠小于網格數量N(K< (13) 式中:Ψ為N×N的單位矩陣。位置向量S在矩陣Ψ下的投影向量為 (14) 所以,向量X∈RN×K同樣具有稀疏性,并且具有可壓縮性,即矩陣中的大部分元素為0或接近于0。 3.2.1 節點連通性的判斷 傳統DV-Hop[14]算法采用距離矢量交換協議,監控區域內的所有節點均可獲得信標節點的跳數信息,網絡規模越大則成本開銷亦越大,會造成較大的浪費。因此,我們的目標是希望利用較少的通信量來做到更準確的定位。 在這里,如果網絡中任意節點通過單跳路由均可和其他節點進行信息交換,則網絡是連通的,進行定位之前信標節點向周圍以r為半徑的圓廣播一個消息,即利用公式(15)判斷節點之間的連通性,若第m個信標節點和第n個網格節點之間的距離dm,n小于信標節點的通信半徑R,則兩個節點之間可以直接通信(單跳),連通性為1;否則無法通信,連通性為0,即 Distancem,n=dm,n (15) 式中:第m個信標節點和第n個網格的歐式距離dm,n為 (16) 通過合理設置信標節點的通信半徑將定位區域等面積劃分,利用邊界框(Bounding-Box)思想將待定位節點位置縮小到某塊可能性區域,形成無縫覆蓋的網絡,最終構造出全連通的網絡。 3.2.2 觀測矩陣分析 壓縮感知的關鍵是觀測矩陣的構造,觀測矩陣性能的好壞直接影響恢復信號和原信號之間誤差的大小。CS理論大多采用隨機矩陣(例如高斯隨機矩陣)作為觀測矩陣,這類矩陣占用的存儲空間較大,且實際應用中很難用硬件實現。本文選用確定性觀測矩陣,考慮用(通信半徑-距離)/通信半徑的算法進行構建確定性觀測矩陣。 當節點之間連通時,觀測矩陣Φm,n被構建為 (17) 當節點之間連通性為0時,觀測矩陣Φm,n權重被設置為無窮小。 作為感知的前端,觀測矩陣主要有以下幾個評價標準:RIP、構造計算復雜度、矩陣維數及重構性能[15]。 (1)RIP:Baraniuk在文獻[16]中提出,RIP的等價條件為稀疏變換基Ψ與觀測矩陣Φ不相關。也就是說,Φ的行Φi不能由Ψ的列Ψj稀疏表示,同時Ψ的列Ψj不能由Φ的行Φi稀疏表示。由于信標節點在網格中均勻分布,而稀疏變換基Ψ的列是一個一階稀疏的向量,顯然,本文所構造的觀測矩陣和稀疏變換基有很強的不相關性。 (2)構造復雜度:本文所構建的確定性觀測矩陣為一次方程,通過簡單的數學運算即可得到。進行存儲或者傳輸時,只需要存儲或者傳輸方程及參數,大大節省了存儲空間,傳輸效率也隨之提高,尤其在矩陣較大時,觀測矩陣的優越性則更為明顯。 (3)矩陣維度:觀測矩陣的維數應盡可能不受限制以適應大面積的實際應用,本文中M為信標節點的個數,N為仿真范圍與步長之比的平方,矩陣的維度較為靈活。 (4)重構性能:見下文對比圖。 本節對本文提出的改進的基于貝葉斯壓縮感知的多目標定位算法進行仿真實驗,并分別與基于DV-Hop的最小二乘定位算法以及基于BCS、OMP的壓縮重構算法進行對比,驗證本文算法定位性能的優越性;然后,分別從定位誤差和定位耗時兩方面研究網絡步長對定位效果的影響。 在Matlab平臺上進行仿真實驗,具體參數設置如表1所示,定位區域設為100 m×100 m的方形區域,感知節點為151個,其中信標節點為121個,其余為未知節點,信標節點的通信半徑為15 m。 表1 仿真場景的參數設置 考慮評價標準的普適性,采用絕對誤差和通信半徑的比值作為定位誤差d: (18) 本文提出的改進算法的效果如圖2所示。 圖2 實際位置和估計位置對比 圖3展示了未知節點進入等面積劃分區域后,充滿隨機性,不像紅色信標節點的坐標均勻分布規則排列。通過將改進的BCS預測出的未知節點位置坐標與通過DV-hop算法、BCS算法、OMP算法預測出的位置進行對比,可以直觀地看出改進觀測矩陣的BCS算法預測定位效果最好,OMP、BCS算法效果次之,各自存在一定的缺陷,DV-hop算法最差,預測效果不夠理想。 圖3 不同算法的定位效果圖 由圖4可以得出,在同一通信半徑R=15 m時,DV-hop算法預測未知節點誤差百分比最大,預測位置與實際位置對比有明顯差距;BCS算法和OMP算法預測定位效果相差不大,定位誤差百分比均較低;改進觀測矩陣的BCS的定位算法節點誤差最低,定位效果最優。由表2可以得出,改進的BCS算法波動最小,OMP的誤差波動不大,原BCS算法的預測誤差波動較大,穩定性較差。圖4和表 2表明,改進觀測矩陣后,BCS的定位精度明顯上升且誤差波動最低。 圖4 不同算法預測節點誤差對比 表2 不同算法預測節點的均方誤差 當通信半徑為15 m時,在傳感器監測區域內,不同的歩長對定位算法的影響如圖5和圖6所示。 圖5 網絡步長對定位誤差的影響 圖6 網絡步長對定位耗時的影響 如圖5所示,當網絡步長增大,可能性區域中的小方格數目減少,定位難度變大,所產生的定位誤差也就越大;在網絡步長為1~4 m時,步長為1.1 m左右定位誤差最小。從圖6可以看出,隨著網絡步長的增長,觀測矩陣的維度也在減少,通信量降低。利用不同算法進行重構時,算法計算量也相應減少,整體上定位耗時隨網絡步長增大而減少。由此可見,步長的設置對定位效果影響較大。而本文設定為固定步長,在稀疏度未知的情況下靈活性較低。 為了解決當前無線傳感器網絡都會存在的低功耗和高性能無法共存的問題,本文設計了一種基于壓縮感知的多目標定位算法。改進觀測矩陣后的BCS定位算法具有良好的重構性能,實現了定位性能與節點能量的均衡考慮。而本文算法是針對靜態多目標進行研究的,在接下來的工作中,將進一步對所提算法進行改進,應用到動態目標定位和稀疏度未知的情況中去,擴大適用范圍。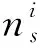
3 改進矩陣設計及分析
3.1 稀疏變換基
3.2 觀測矩陣
4 實驗仿真與結果分析
4.1 仿真場景

4.2 實驗結果及分析

5 結束語

