凍結砂土層中埋地管道管土界面應力分析

王一民,王凱勃，徐 艷，王尊策,盧召紅

(1.東北石油大學，黑龍江大慶 163318;2.中國石油 大慶石化分公司，黑龍江大慶 163714)

0 引言

寒區埋地管道由于氣溫長時間處于0 ℃以下，會導致埋地管道周圍的土體發生凍脹現象，此時管道與土體之間的力學性能就會發生改變，嚴重時可能會對管道輸送的安全產生不利影響[1]。因此，研究凍土地帶管道與土體之間的界面應力問題，可以為保障管道運輸的安全提供理論支撐。

埋地管道與土體間的相互作用一直以來被眾多學者所關注。黃龍等[2]歸納了凍土區管道工程的研究現狀及發展過程，總結了室內外管土相互作用的相關試驗、數值模擬分析和理論分析方法。劉全林等[3]建立了管土相互作用的彈性組合模型，得出管-土接觸面上不僅有正應力還有剪應力，同時考慮埋地管道埋設條件、回填介質對管土相互作用的影響，建立了管土相互作用平面問題的傳遞矩陣分析法。在此基礎上，張坤勇等[4]考慮開挖引起的地層位移對地下管線應力和變形的影響，建立了任意載荷條件下管線的理論公式，將理論計算結果與有限元分析計算結果進行了比較，驗證了解析方法的可靠性。張海豐等[5]針對埋地管道周圍土壓力分布規律、管道內部應力特征、管道破壞機理以及填土對管道受力狀態的影響等，利用土箱模型試驗研究了上述因素下的管土相互作用問題。QIN等[6]通過管土相互作用數值分析模型，利用平面應變抗剪強度參數表征了數值模型中的回填砂，考慮彈性模量隨深度的變化關系，得出了一種新的關于應力-位移曲線的本構模型。

本文根據上述研究，采用雙線性界面內聚力有限元分析模型，建立凍結砂土與管道相互作用分析模型，研究凍土與管體軸向載荷作用下的界面應力問題，通過試驗驗證有限元分析模型的可靠性，為進一步研究埋地管道局部損失、腐蝕坑應力集中致損問題奠定基礎。

1 管土層間界面切向應力位移本構試驗

1.1 試驗概況

試驗主要研究確定凍結砂土的基本物理性能和冰凍條件下砂土與埋地管道間的界面應力[7-8]。試驗設備包括JPW-10型電液伺服加載裝置系統、數據采集系統、標準型ELDyn凍土動靜三軸測試系統和自制試驗土箱等。

試驗土箱模型尺寸為：1 000 mm×580 mm×600 mm(長×寬×高)，土箱由10層40 mm×40 mm方鋼管組成，采用螺栓連接每層方鋼管，相鄰兩層槽鋼間隙為20 mm。采用3 mm厚鋼板焊于土箱底部和前后兩側作為土箱擋板。前后擋板中間預留一直徑為40 mm的管道安裝孔。模型尺寸和管徑均滿足幾何尺寸相似關系，同時考慮了試驗土箱模型尺寸受試驗裝置、土壤質量和管道模型尺寸等因素的影響。

加載裝置的水平載荷作用于管道的自由端，加載方式為位移控制，加載速率為0.05 mm/s，當加載點一端的管土界面力趨于穩定時，載荷終止，即加載端產生管土分離現象。試驗得出的結果可根據相似關系，應用到實際工程中的大管徑問題。試驗裝置及試件實物圖和結構見圖1。

(a)試驗裝置及試件

(b)試驗土箱與試件結構示意圖1 試驗裝置及試件實物圖與結構示意Fig.1 The actual photo and schematic diagram ofthe test device and specimen

1.2 凍結砂土基本物理參數測定

為了得到凍結砂土的基本物理參數，制作了3個標準凍結砂土樣本測試，以確定凍結砂土的物理性質。砂土顆粒級配圖如圖2所示。

圖2 砂土顆粒級配圖Fig.2 Sand particle grading map

制備含水率為7%的試驗土樣，采用環刀法，根據式(1)和式(2)計算土樣的干密度。

ρo=mo/V

(1)

式中，ρo為土樣的濕密度,g/cm3；mo為土樣的質量,g；V為土樣的體積,m3。

(2)

式中，ρd為土樣的干密度,g/cm3;wo為土樣的含水率,%。

非飽和狀態下砂土在-18～-20 ℃冬季寒冷環境下凍結24 h，通過無限壓縮試驗測定了土樣的壓縮特性，測量的應力-應變曲線如圖3所示。分別在100,200,300 kPa三種圍壓下對試驗土樣進行三軸剪切試驗，每種圍壓下試件做3組試驗取其平均值，凍結砂土試驗土樣剪切應力-位移曲線如圖4所示。采用三軸壓縮試驗測得土樣的粘聚力和內摩擦角，三軸測試系統見圖5。試驗測定各土樣基本物理參數平均值如表1所示。

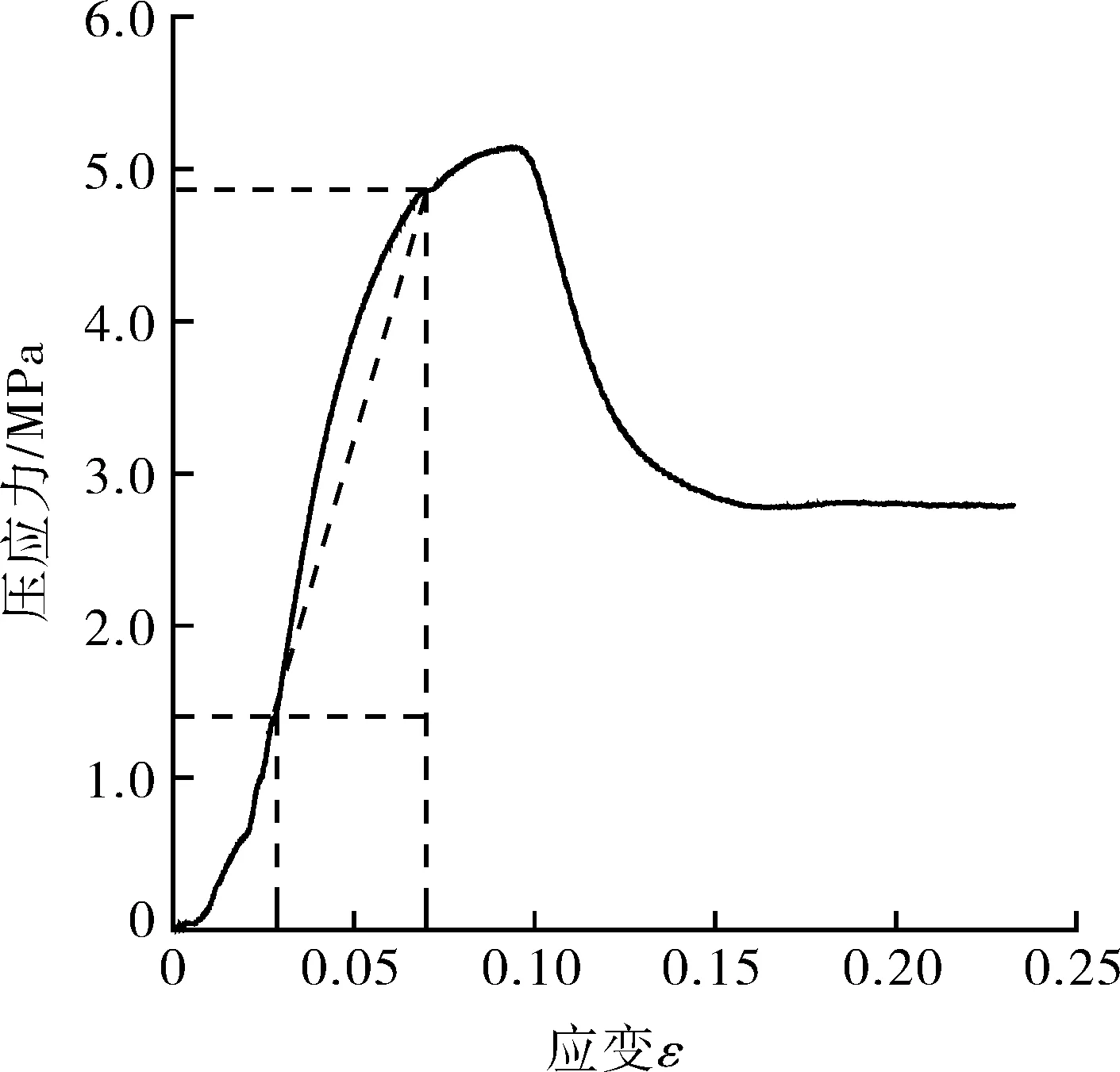
圖3 凍結砂土試驗土樣應力-應變曲線Fig.3 Compression stress-strain curve of frozensand soil sample

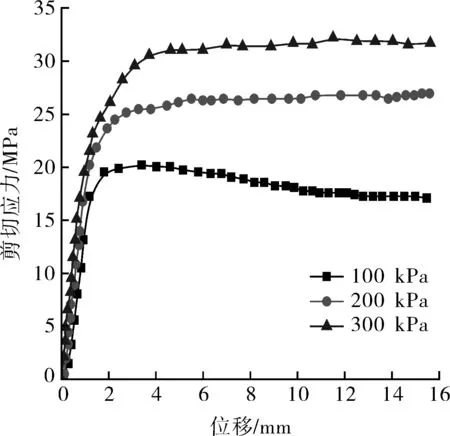
圖4 凍結砂土試驗土樣剪切應力-位移曲線Fig.4 Shear stress-strain curves of the frozensoil samples

圖5 標準型ELDyn凍土動靜三軸測試系統Fig.5 Standard ELDyn frozen soil dynamic andstatic triaxial test system

表1 土樣的基本物理參數Tab.1 Basic physical parameters of soil samples

根據圖3,4所示的試驗結果，凍結砂土的動彈性模量可用式(3)計算：

(3)

式中,ECS為凍結砂土的動彈性模量,MPa；σCS為壓應力,MPa；εCS為壓應變。

1.3 管道力學性能參數

試驗截取了3根長度相同、使用狀況相同的鋼管，并對3次試驗結果取平均值。管道材料基本力學性能如表2所示，為盡可能模擬實際工程中管道處于凍結砂土中的狀態，將管道埋置在靠近土箱模型中間位置，以減小土箱壁對于試驗結果的影響，減小誤差，故管道中心埋置深度為300 mm，管道直徑D小于0.1倍的埋置深度。沿管道軸向均勻布置5個應變片，應變片的間距為210 mm，標號分別為Y1,Y2,Y3,Y4,Y5，如圖6所示，采用全橋式應變片粘貼方式。使用數據采集裝置采集試驗管道的應力、應變值。

表2 管道主要材料性能參數Tab.2 Material performance parameters of the pipe

圖6 應變片布置示意Fig.6 Schematic diagram of strain gauge layout

1.4 試驗結果與分析

根據凍結砂土層中管土相互作用試驗得出的數據，用差值法計算得到管土界面剪應力-位移關系曲線，計算方法如式(4)～(7)所示。

τ=V/A

(4)

式中，V為兩測點間的剪切力,MPa，V等于試驗管道在兩個相鄰測點間所受的拉力差值，即V=∣Ti-Ti+1∣；A為相鄰測點間的管土接觸面積,mm2。

V=∣εi-εi+1∣Ed2πR

(5)

式中，εi,εi+1分別為相鄰兩測點試驗管道表面應變值；E為試驗管道的彈性模量；d為試驗管道壁厚,mm；R為試驗管道外徑,mm。

A=(li+1-li)2πR

(6)

式中，li,li+1分別為相鄰兩測點至Y1的距離,mm。

τ=ΔεEd/Δl

(7)

經過對采集數據進行分析，發現Y4，Y5兩測點的結果比較穩定，利用Y4，Y5對應的應變值，按式(7)計算出管土間的界面剪應力，繪制管土界面剪應力-位移曲線，如圖7所示。

圖7示出在凍結砂土層中，管道受軸向拉力作用時，曲線分為三個階段。首先管土界面處的剪應力隨管道變形增大而增大；達到極限應力后，管土相互脫離，界面剪應力驟減；管土繼續發生相對位移，管道與土體間的凍結力與粘聚力影響逐漸減小，管道與土體之間的滑動摩擦力逐漸占據主導地位，此時曲線慢慢趨于平緩，由于此階段對于研究管土之間界面應力影響較小，可忽略此階段。凍結砂土中管土界面處的最大界面剪應力為392.9 kPa，此時管道變形值為57.3 mm，達到極限應力后界面剪應力減小至203.4 kPa，隨后趨于平緩，管土相對位移增大至77.4 mm。管道受凍脹影響，會使管道局部抬升，由于抬升處左右兩側界面應力過大，會使管道在抬升處應力集中過大，從而發生管道破壞事故。

圖7 凍結砂土中管土界面剪應力-位移曲線Fig.7 Shear stress-displacement curve of pipe-soilinterface in frozen sand

2 管土層間界面應力有限元分析

2.1 基本假定

在建立凍結砂土與埋地管道相互作用有限元分析模型時，采用如下基本假定：(1)凍土是一個小的彈性空間體，管道與周圍土壤之間的界面位于空間的無彎曲表面;(2)根據圖7所示的試驗結果，可假定管土界面剪應力-位移關系為雙線性本構關系，管道與凍結砂土之間的界面應力完全符合管土界面應力的分析模型。

2.2 模型建立

借助ABAQUS有限元分析軟件，建立有限元分析模型[9-10]，土體和管線均采用C3D8R單元建立，模型大小與試驗中的一致。土體采用摩爾-庫倫塑性賦予粘聚力和內摩擦角度[11]，材料本構關系采用試驗研究部分測定的數據。利用有限元軟件中的初始邊界條件將土體三面固定，土體與管道之間的相互作用[12]采用基本假定第二條中的雙線性剪應力-位移關系來表征其本構關系。在有限元分析軟件中，雙線性內聚力模型[13-14]是廣泛采用的一種本構關系模型，界面粘結力在外載荷作用下，初始剪應力與位移呈線彈性變化關系，應力達到最大值τm后，界面出現損傷并不斷擴展，剪應力-位移關系進入線性軟化階段，直至最終完全脫離失效，其具體形狀如圖8所示。其切向T-S關系控制方程如下:

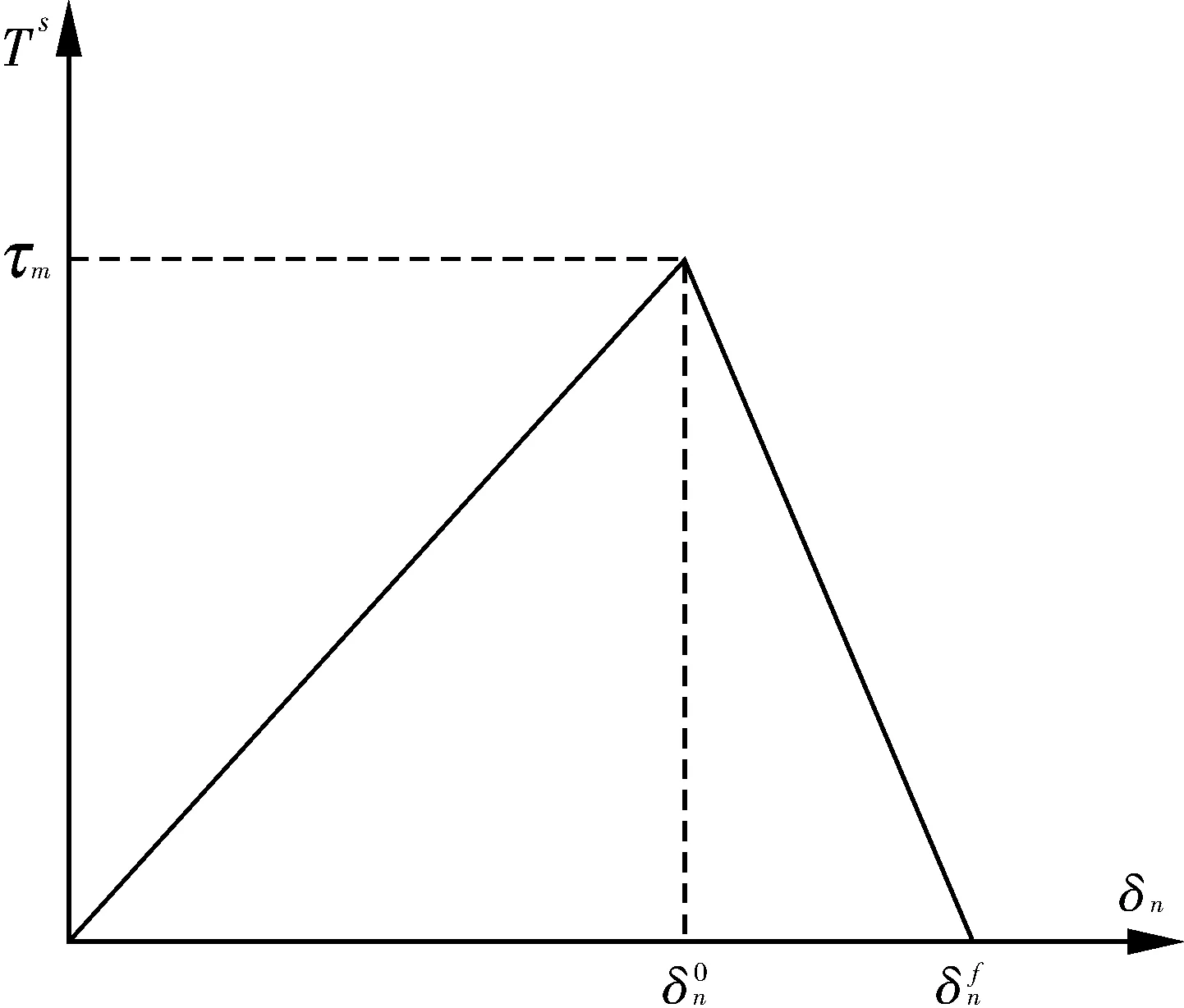
圖8 雙線性界面剪應力-位移關系模型Fig.8 Bilinear interface shear stress-displacementrelationship model

(8)

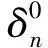
2.3 有限元結果與分析

在ABAQUS模擬軟件中得到應力云圖如圖9所示。將試驗與有限元分析結果作對比分析，如圖10所示，試驗值與有限元分析值基本吻合。

圖10示出埋地管道管土界面應力-位移關系。有限元分析模型取土的彈性模量為常數，界面應力與相對位移兩者之間是線性關系，此時可以認為凍土在一個小變形范圍內為彈性體，試驗結果與有限元分析結果誤差為3.97%，兩者結果基本吻合。由于在有限元模擬時管土的相互作用本構模型采用的是雙線性內聚應力-分離位移關系模型，該模型認為界面應力在達到峰值后一直下降直至消失，所以有限元曲線相較于試驗曲線無水平段。而實際試驗中管土完全脫離之后，管土之間的相互作用變為滑動摩擦，所以試驗曲線中有近似水平段出現，并且凍結砂土的動彈性模量ECS受溫度、圍壓、密實度等因素的影響較大[15-16]，而有限元分析模型并未考慮這些因素，導致試驗值與理論值有一定誤差。

(b) 管道應力云圖圖9 管土相互作用有限元分析結果Fig.9 Finite element analysis results ofpipe-soil interaction

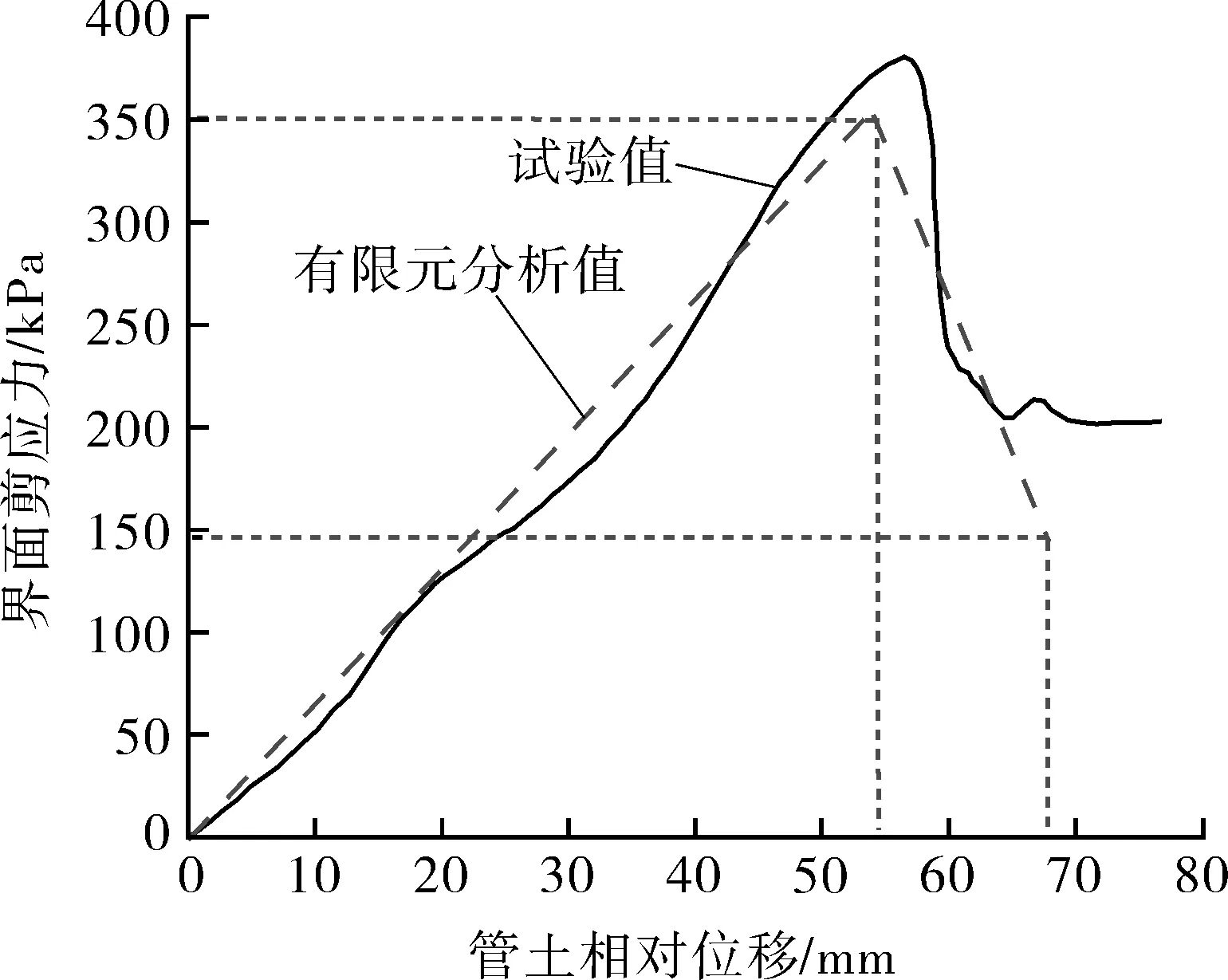
圖10 埋地管道管土界面剪應力-位移關系Fig.10 Shear stress-displacement relationship ofpipe-soil interface of buried pipeline

實際試驗中由于試驗條件的限制和人為條件的影響，試驗得出的曲線并不是兩條直線，但總體趨勢呈雙線性。本文采用有限元方法建立的雙線性粘聚模型與試驗值的誤差小于5%，在工程誤差允許范圍之內，為進一步研究埋地管道局部損失、腐蝕坑應力集中致損問題奠定基礎。未來在本模型基礎上還可進行凍結砂土層中埋地管道在復雜應力場條件下的管土界面應力作用分析，例如在地震或其他外力作用下引起的管道變形與位移，研究此時的管土界面應力也可為寒區管道運輸的設計與防災減災提供理論依據。

3 結論

(1)根據凍結砂土層中管土相互作用試驗，管土界面剪應力-位移關系曲線可以簡化為兩個階段，由此建立了雙線性管土間界面剪應力-位移本構模型。

(2)根據雙線性管土界面剪應力-位移本構模型，建立了凍結砂土與埋地管道界面應力有限元分析模型，研究了凍土層中埋地管道管土的相互作用。將有限元分析結果與試驗結果進行對比分析，驗證了有限元模型的準確性。因此該有限元分析方法可用于計算寒區凍土層埋地管道在軸向剪切力作用下的管土界面應力。

(3)通過對試驗、理論和有限元模擬分析得出的曲線進行比較，發現這3種曲線趨勢一致。因此假定凍土是一個彈性較小的空間體，管道與周圍土壤之間的界面位于空間的無彎曲表面是合理的，同時也證明本文建立的雙線性管土間界面剪應力-位移本構模型是正確的。

(4)建立的有限元模型用于模擬計算凍結砂土內管-土之間的軸向界面應力，有限元分析結果與試驗結果的誤差為3.97%，較為吻合。由于管土相互作用本構模型與實際管土接觸情況略有差異且凍結砂土的動彈性模量受圍壓、密實度等因素的影響較大，而有限元模型中未考慮這些因素，這是誤差產生的主要原因。