基于模糊控制的自動駕駛汽車爆胎控制

陳齊平，王 亮，羅玉峰，謝加超，劉 權

（華東交通大學 載運工具與裝備教育部重點實驗室，南昌 330013）

0 引言

在人工智能的大背景下，自動駕駛汽車日益突出，但其出行的安全和高效得到廣泛的關注。但自動駕駛汽車行駛過程中輪胎也會出現爆胎工況，其徑向、縱向和側向動力學特性都發生突變[1]，容易導致車輛駛入其它車道甚至翻車等事故。根據美國統計數據可知[2]，由于爆胎導致的車禍達到近9萬起，引起400多人死亡，約1000人受傷。而當車輛高速行駛時，輪胎的機械損傷和熱損傷積累易導致車輛發生爆胎，因此，研究基于模糊控制的自動駕駛汽車爆胎控制有著重要意義。

天津大學胡超芳[3]通過模型預測控制的方法對自動駕駛汽車爆胎控制，提高了系統響應速度和控制精度，車輛非線性運動位姿在轉化成線性過程中有少量誤差。廣西工學院張彥會[4]采用模糊控制算法，能有效控制了爆胎車輛跑偏，但較少對爆胎車輛的橫向位移進行分析。胎壓檢測是預防爆胎的一種重要手段[5]，但自動駕駛汽車中視覺傳感器CCD、激光傳感器易受環境影響，車輪容易駛入凹凸路面導致車輛爆胎，很難從根本上解決問題。基于輸入狀態魯棒性控制的爆胎研究提高車輛爆胎穩定性控制，研究過程中較少考慮到最優輸入[6]。利用差動制動方法，通過線性二次型調節器LQR有效地控制車輛爆胎后操縱穩定性，但需要借助實時特性確定加權矩陣[7]。利用增益可變的PID控制器能有效地控制爆胎軌跡[8]，出現較少偏差后調整到原路徑，橫擺角速度數值是決定乘客乘坐車輛舒適性重要因素之一，從實驗結果可知，橫擺角速度波動較大。

本文針對自動駕駛汽車爆胎控制存在的不足，首先建立線性二自由度車輛模型，自動駕駛汽車因爆胎導致輪胎參數發生劇烈變化，為此，根據附著橢圓理論，本文根據點剎和微調前輪轉向角的方式設計了模糊控制器，最后通過Carsim與Simulink聯合仿真，結果表明基于模糊控制的自動駕駛汽車爆胎控制方法能有效控制爆胎，提高車輛安全性和穩定性。

1 爆胎后偏航原因分析

輪胎發生爆胎后，其參數發生顯著變化，滾動阻力系數增加20多倍，側偏剛度下降原來0.28倍左右[9]，爆胎引起的參數變化，如圖1所示。

圖1 爆胎引起的參數變化

由圖1(b)可知，左前輪爆胎其滾動阻抗系數瞬間增大，右前輪保持不變，因地面對左右輪滾動阻力不同使自動駕駛汽車產生逆時針轉矩，從而導致汽車向左發生偏航。在無控制的工況下，自動駕駛汽車通過傳感器、視覺算法等感知位姿，獲得電信號通過CAN總線傳輸到自動駕駛汽車VCU系統，系統形成執行信號通過CAN總線給轉向電機，使自動駕駛汽車向右行駛。而由圖1(a)可知，爆胎后輪胎側偏剛度下降，導致地面提供側向力減小，不足以使車輛右轉，因此自動駕駛汽車極易制動跑偏和側滑，甚至發生翻車等事故。

2 線性二自由度車輛模型

為簡化模型復雜程度，通過等效的自行車模型的方法，建立線性二自由度車輛模型，如圖2所示。其中Pxy是車體坐標系。

圖2 線性二自由度車輛模型

由圖2可知，二自由度自動駕駛汽車的動態方程如下：

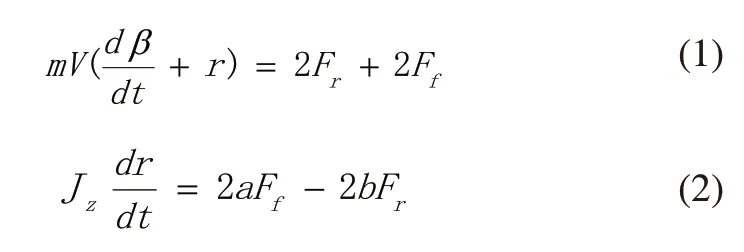
其中，m表示汽車的質量，Jz表示轉動慣量，δ表示前輪轉向角，r表示橫擺角，β表示質心側偏角，a表示車輛質心到前軸的距離。b表示質心到后軸距離。V表示質心速度，Ff和Fr分別表示地面作用于前、后輪胎的側偏力。

其中，βf表示前輪側偏角，βr表示后輪側偏角，Kf表示前輪側偏剛度，Kr表示后輪側偏剛度。將式(3)、式(4)代入式(1)、式(2)得：

由式(5)、式(6)可建立線性二自由度車輛Simulink模型，通過車輛動力學仿真軟件Carsim內部求解出整車轉向角δ和質心車速V，求解量輸入到自動駕駛汽車線性二自由度車輛模型中，輸出質心側偏角β和橫擺角速度r。

3 控制器設計

3.1 附著橢圓理論

車輛因爆胎導致輪胎參數改變發生偏航，因此，車輛彎道行駛受到地面對輪胎產生側向力。車輛處于制動工況，制動力和側向力平方和最大值為常數；車輛處于驅動工況，驅動力和側向力平方和最大值也為常數[10]。

其中，acmax表示最大附著加速度，為常數，ay表示側向加速度，axb表示制動時縱向加速度，axf表示驅動時縱向加速度，由牛頓第二運動定律近似可知：

其中，Fcmax表示最大附著力，為常數，Fy表示側向力，Fb表示制動時縱向力，Fa表示驅動時縱向力。自動駕駛汽車超過最大附著力，輪胎就會出現打滑等危險工況。力可以通過幾何關系表示，即附著橢圓，如圖3所示。

圖3 附著橢圓

汽車發生爆胎后導致輪胎參數改變，輪胎力學性能下降，因此地面作用于輪胎的縱向力和側向力平方和減小，即最大附著力減小。根據附著橢圓理論，本文提出通過點剎與微調前輪轉向角的方式，用于控制爆胎后自動駕駛汽車穩定性，點剎與微調前輪轉向角分別均降低爆胎自動駕駛汽車受到的地面縱向力和側向力，因此使縱向力、側向力和最大附著力仍滿足附著橢圓理論，可充分利用地面附著系數使自動駕駛汽車安全制動和穩定性。

3.2 模糊控制

通過分析，采用點剎與微調前輪轉向角的方式不需要建立準確的數學模型，通過模糊規則可設計模糊控制器[11]，但須結合合理的經驗。當爆胎車輛質心側偏角較小時，以橫擺角速度的控制為主，當爆胎車輛質心側偏角較大時，以質心側偏角控制為主[12]。車輛因爆胎導致偏航，則車速是影響車輛橫擺角速度大小重要因素之一，因此質心側偏角和車速是模糊控制器的輸入，根據附著橢圓理論確定模糊控制器輸出為輪缸制動壓力和轉向角。MATLAB中開發出多達11種隸屬度函數，比較典型的有梯形隸屬函數（trapmf）和三角形隸屬函數（trimf）等。本文采用三角形隸屬度函數，MATLAB表示為：

其中，參數A表示三角形左“腳”數值，參數C表示三角形右“腳”數值，參數B表示三角形“峰”值。三角形隸屬度函數表達式如下：

其中車速模糊集論域為[0，120Km/h]，分為5級。質心側偏角論域為[0，13deg]，分為12級。轉向角論域為[0，17deg]，為實現較高的控制精度，分為16級。補償制動壓力論域為[0，11Mpa]，分為16級。模糊變量隸屬度函數，如圖4所示。

圖4 模糊變量隸屬度函數

根據附著橢圓理論，車輛高速爆胎瞬間，輪胎參數發生突變導致最大附著力減小，控制制動輪缸輸出較小制動力，轉向盤輸出較小轉向角，防止輪胎縱向力與側向力突破最大附著力，因此提高車輛穩定性。車速較低，控制制動輪缸輸出較大制動力，轉向盤輸出較大轉向角，可充分利用最大附著力來減小車輛偏航程度，因此提高車輛制動安全性。通過隸屬度函數，分別建立了質心側偏角和車速與轉向角、質心側偏角和車速與制動壓力的模糊規則。模糊控制規則表，如表1所示。

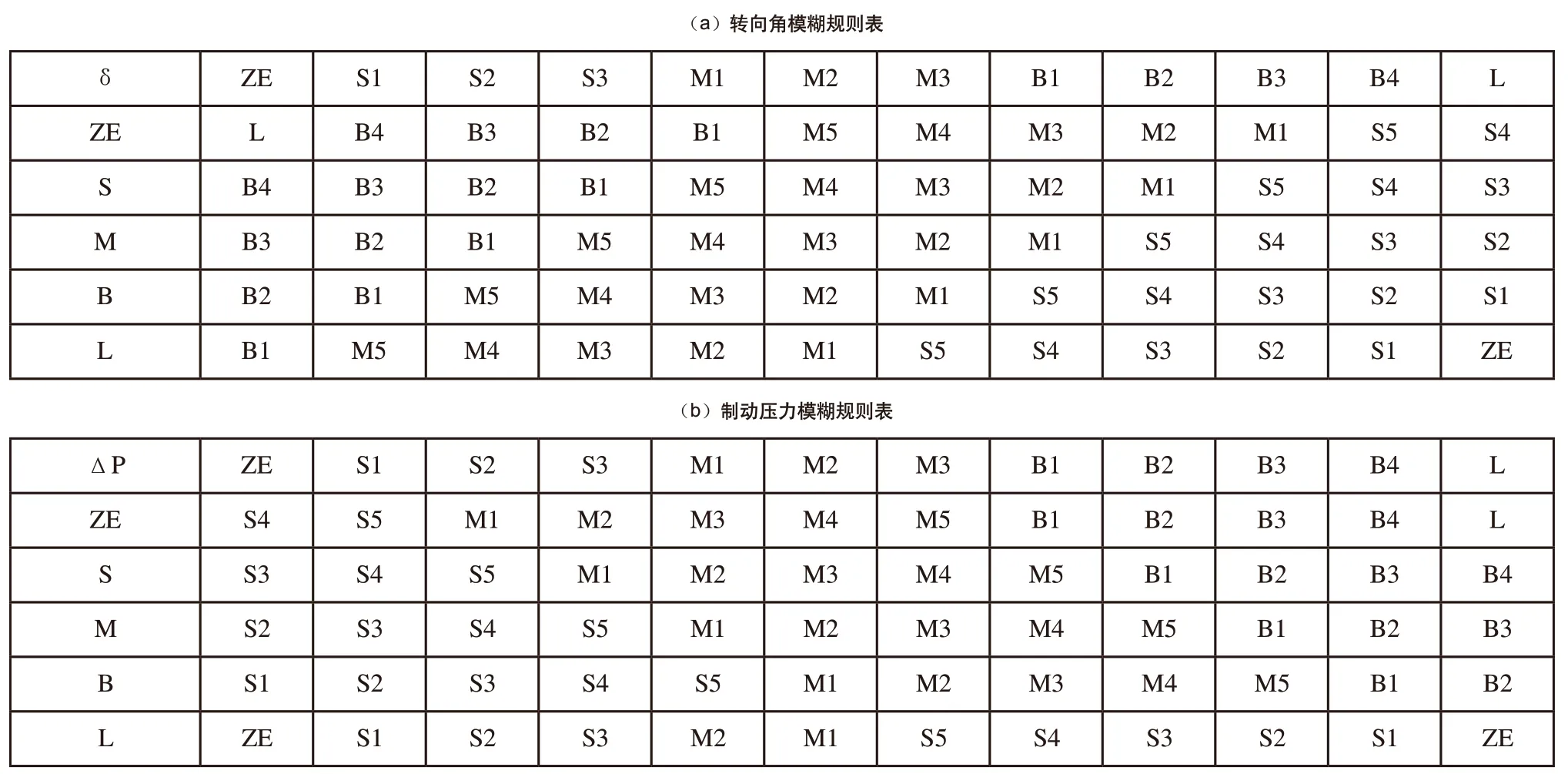
表1 模糊控制規則表

模糊控制器根據質心側偏角β和質心車速V確定所需補償制動壓力ΔP，補償制動壓力ΔP再分配到所需爆胎輪缸。分析爆胎后偏航原因可知，爆胎引起的輪胎參數發生突變無法通過Carsim實現，因此，在建立線性二自由度車輛Simulink模型中，側偏剛度Kf和Kr變化可運用Simulink中工具箱Signal Builder模塊完成。將爆胎導致輪胎參數變化模型通過二自由度Simulink模型導入到Carsim軟件，實現仿真模型搭建。

由模糊控制器確定補償制動壓力ΔP和前輪轉向角δ之后，建立Carsim和Simulink聯合仿真模型，如圖5所示。聯合仿真模型主要由線性二自由度車輛模型、模糊控制模塊和ABS防抱死模塊組成。ABS模塊輸入分別為車輛質心速度V、模糊控制器確定補償制動壓力ΔP、制動輪缸壓力和各輪缸車速，輸出四個輪缸的最終制動壓力。Carsim設置車輛第4秒左前輪發生爆胎，模糊控制器確定的補償制動壓力ΔP僅輸入到ABS模塊左前輪制動輪缸，其它制動輪缸制動壓力保持不變。

圖5 Carsim和simulink聯合仿真模型

4 爆胎控制仿真

車輛參數，如表2所示。車身結構參數、懸架參數、輪胎參數等直接利用Carsim模型默認值，進行了車速、縱向位移、橫向位移、橫擺角速度、左右前輪制動壓力的仿真。

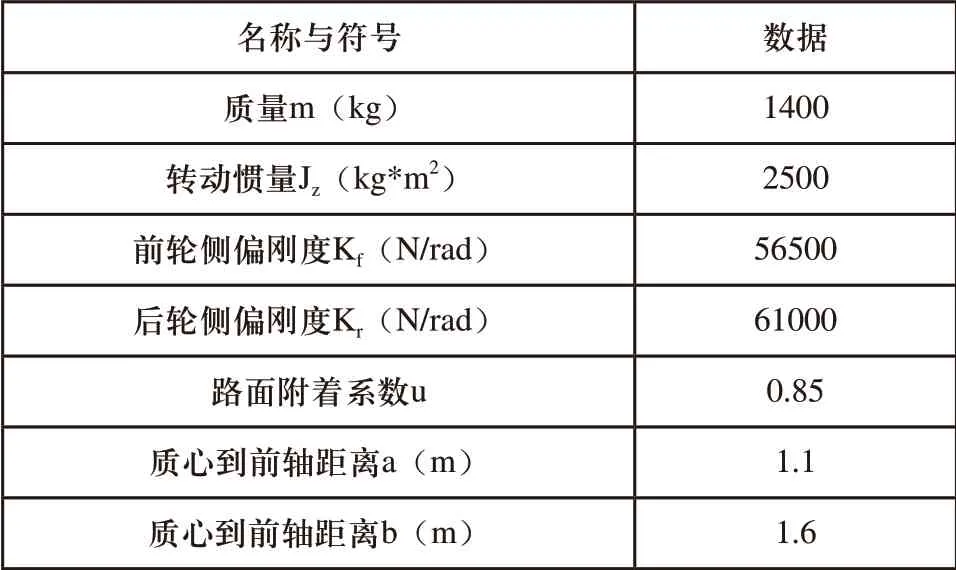
表2 車輛參數

自動駕駛汽車爆胎之前在附著系數0.85路面以120km/h直線行駛，節氣門開度為0，設置車輛在第4秒時左前輪發生爆胎，仿真過程中不考慮爆胎輪胎垂向剛度變化，爆胎0.2秒之后，CO增大20多倍，Kf下降為原來的0.28倍[9]，通過模糊控制仿真實驗，車速和縱向位移，如圖6所示。

圖6 車速和縱向位移

由圖6(a)可知，自動駕駛汽車在路面附著系數為0.85的路面上，節氣門開度為0，滑行4秒車速從120km/h減速到110km/h，經過爆胎控制，車速在8.2秒左右減速到0。由圖6(b)可知，自動駕駛汽車在4.2秒時，縱向位移達到146m左右；車速為0時，縱向位移約為175m。在爆胎制動控制過程中，制動距離約為29m。傳統汽車初速度110km/h制動成績約為40m，通過對比，這由于車輛發生爆胎滾動阻力系數瞬時增大，制動距離減少約11m。通過模糊控制仿真實驗，橫向位移和橫擺角速度，如圖7所示。

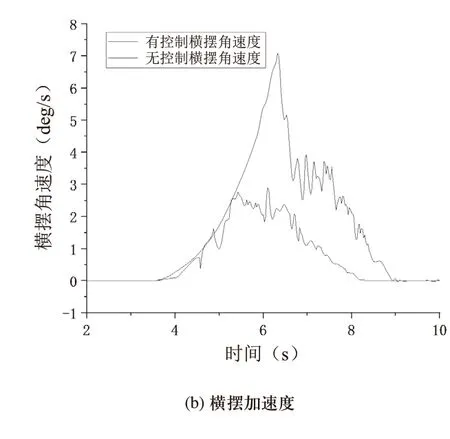
圖7 橫向位移和橫擺角速度

由圖7(a)可知，自動駕駛汽車爆胎后，無控制時橫向最大位移接近6m，有控制時橫向最大位移減小到2m。由圖7(b)可知，自動駕駛汽車爆胎后，通過點剎的控制，在模糊控制介入作用下，有控制時橫擺角速度在爆胎之后2s左右遞增到2.5deg/s，微調前輪轉向角方向使橫擺角速度減小，自動駕駛汽車偏航程度也隨之減小。無控制時橫擺角速度達到7.5deg/s，后保持在3deg/s。由于左前輪發生爆胎，左前輪滾動阻力比右前輪大。無控制時，自動駕駛汽車爆胎后驅動力、制動力和側向力突破了最大附著力，導致車輛發生側滑甚至輪胎脫輞，因此，橫向位移和橫擺角速度顯著增大。根據附著橢圓理論設計的模糊控制器，使左前輪輪缸爆胎開始采用點剎方式，左前輪輪缸制動壓力處于動態平衡中，防止左前輪縱向力和側向力突破最大附著力，提高車輛穩定性。而右前輪制動強度大，充分利用最大附著力，因此提高車輛制動安全性，實現穩定性控制。通過模糊控制仿真實驗，輪缸制動壓力，如圖8所示。

圖8 輪缸制動壓力

由圖8(a)和圖8(b)可知，車輛左前輪爆胎時，在模糊控制器介入的工況下，通過模糊控制規則獲得間斷的制動壓力，右前輪獲得相對連續的制動壓力，左前輪滾動阻力比右前輪大，但左前輪為間斷制動壓力，仍能滿足最大附著力。因此，左、右前輪制動壓力符合附著橢圓理論，滿足模糊控制規則，進一步證明Carsim和Simulink聯合仿真模型的準確性。

5 結語

針對自動駕駛汽車存在爆胎的問題，基于附著橢圓理論，本文提出了點剎和微調前輪轉向角的方式建立模糊控制器，不需要建立具體的數學模型，能夠較好地輸出自動駕駛汽車爆胎后各輪缸所需補償制動壓力ΔP和前輪轉向角δ，從而使爆胎后縱向力和側向力平方和滿足最大附著力。對車速、縱向位移、橫向位移、橫擺角速度、左右前輪制動壓力進行了仿真分析，結果表明：自動駕駛汽車發生爆胎后，無控制橫向最大位移接近6m，有控制橫向最大位移減小到2m；無控制橫擺角速度達到7.5deg/s，后保持在3deg/s，有控制橫擺角速度在爆胎之后2s左右遞增到2.5deg/s隨之減小，提高車輛制動安全性和穩定性。