基于子集模擬的建設工程項目多資源均衡優化算法

王家，劉可心，張學清，陳濤

（1.湖南大學 土木工程學院，湖南 長沙 410082；2.湖南大學建筑安全與環境國際聯合研究中心，湖南長沙 410082；3.香港科技大學 土木與環境工程系，香港 999077；4.長沙市美的房地產開發有限公司，湖南 長沙 410082）

建設項目的施工過程需消耗大量的人工、材料、機械等資源.如果建設項目實施過程中的資源計劃（勞動力計劃、材料進場計劃、機械排班等）安排不合理，會引起建設項目工期內資源消耗量的過大波動（表現為施工人員的窩工或少工、材料和機械的過度使用或空置等），最終影響建設工程的生產效率、成本節約和項目管理質量[1].作為資源調度優化的手段之一，資源均衡問題（Resource Leveling Problem，RLP）旨在通過調整項目中非關鍵工序的計劃開始時間，在不延長項目工期和不違反各工序間邏輯關系的前提下，降低項目工期內資源消耗量的波動.

針對資源均衡問題的研究工作可分為兩類，一類偏重于資源均衡問題的模型構建，一類偏重于資源均衡問題的優化算法.資源均衡優化模型一般可歸結為四類：簡單的平方和模型[2-3]、考慮實際資源消耗量與期望值之間差值的偏差模型[1，4-5]、考慮不同周期資源消耗量變動的波動模型[6-7]、以及基于熵理論的熵模型[8-9].資源均衡問題的優化算法主要分為精確算法和啟發式算法.其中，精確算法主要基于動態規劃、整數規劃、分支定界法等方法[10]，而啟發式算法主要基于蟻群算法[11]、粒子群算法[12]、禁忌搜索算法[13]、遺傳算法[14-18]等算法.資源均衡問題的復雜程度隨涉及工序數量的增加而急速上升.因此，針對工序數量較多的項目資源均衡問題，精確算法并不適用，只能采用啟發式算法.但是，啟發式算法具有隨機性，其每次運行獲得的最優解不一定相同（不穩定），但現有啟發式算法在最優解獲取穩定性上仍有較大的改進空間.

本文針對建設工程項目的多資源均衡優化問題，提出一種基于子集模擬的啟發式優化算法.同時，為避免工序間邏輯關系違反時復雜修復算子的使用，本文采用間隔率變量表示的建設工程項目多資源均衡優化模型，以簡化基于子集模擬的優化算法的操作.通過算例驗證，與應用較廣的遺傳算法相比，本文提出的優化算法在最優解獲取穩定性上有較好的改進.

1 建設工程項目多資源均衡優化模型

針對建設工程項目的多資源均衡優化問題，研究者一般借助網絡計劃工具進行分析，并在一定的假設下構建模型.本文研究的多資源均衡優化模型基于以下假設：

1）組成建設項目的各個工序必須連續施工，不能間斷，且各工序間的邏輯關系不隨時間改變.

2）組成建設項目的各個工序在實施期內，單位時間內耗費資源的種類和數量保持不變.

3）建設項目的總工期保持不變.

考慮一個包括N 個工序、且實施過程中涉及K種資源的建設工程項目.設項目中每一個工序i 的持續時間為Di，i=1，…，N，其持續時間內每單位時間消耗的第k 種資源為，k=1，…，K.根據各工序的持續時間和相互間的邏輯關系，可采用關鍵路徑法（Critical Path Method，CPM）計算出各工序的最早開始時間ESi和最晚開始時間LSi，i=1，…，N，以及項目的總工期T.

建設工程項目多資源均衡優化的目標是通過合理安排各工序的計劃開始時間Si，i=1，…，N，使項目實施期內資源消耗的波動最小.考慮到各工序間的邏輯關系和項目總工期T 保持不變的要求，各工序的計劃開始時間Si，i=1，…，N 需滿足下述限制：

式中：pred（i）代表工序i 的所有緊前工序的集合.

在給定各工序的計劃開始時間S=[S1，S2，…，SN]下，項目在總工期T 內任意時刻t 所消耗第k 種資源的數量（S），t=1，…，T，k=1，…，K，可由該時刻正在施工的所有工序所消耗第k 種資源的數量匯總得到，即：

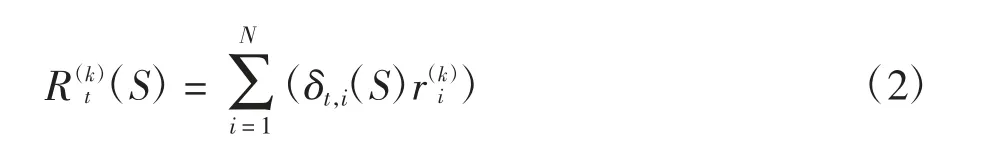
式中：δt，i（S）為t 時刻工序i 是否正在實施的指示變量，δt，i（S）=1 如Si≤t ≤Si+Di（t 時刻工序i 正在實施，如圖1 所示），否則δt，i（S）=0，，k=1，…，K 為工序i 單位時間內第k 種資源的消耗量.

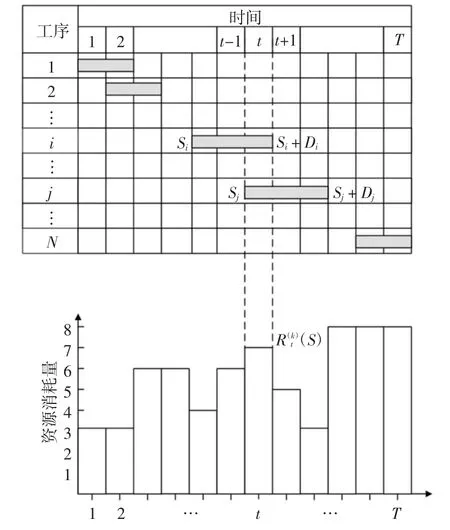
圖1 資源消耗量Fig.1 Resource consumption

在得到項目總工期內施工所需各資源在不同時刻的消耗量后，可計算出用于衡量項目資源均衡效果的指標.針對資源均衡問題，研究者從不同角度出發，提出了反映資源消耗量不均衡程度的多種指標，但學術界尚未在各指標的優劣上達成共識.從統計學角度看，標準偏差指標可較好地反映項目在不同時刻資源消耗量的不均衡程度，在資源均衡優化問題中采用較廣[12，16，19].因此，本文采用標準偏差指標來構造建設工程項目多資源均衡優化模型，但文中所提出的多資源均衡優化算法與所選指標無關，亦適用于其他指標的情形.基于項目在總工期內任意時刻t 所消耗第k 種資源的數量（S），t=1，…，T，k=1，…，K，總工期內第k 種資源消耗量的標準偏差 為σ（k）（S）：

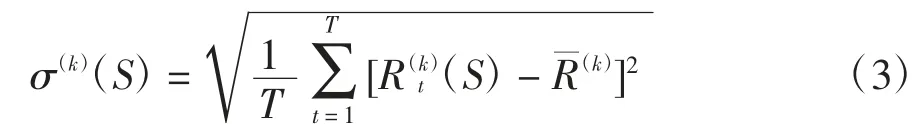
在項目多資源均衡優化問題中，為消除不同資源消耗量數量級、單位等的影響，本文將標準偏差無量綱化，采用標準偏差與平均消耗量的比值σ（k）（S）/來代表每一種資源的均衡效果.同時，為反映不同資源在多資源均衡優化問題中的重要性，可針對不同資源分配不同的權重系數，將目標函數定義為不同資源無量化標準偏差的線性加權：

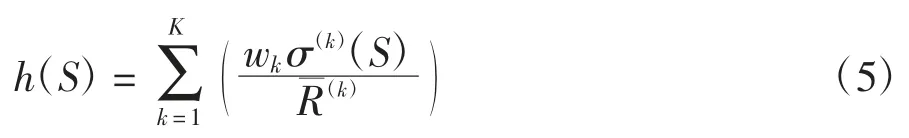
式中：wk為第k 種資源的相對權重，滿足=1，可采用層次分析法和德爾菲法、專家模糊綜合評分法、基于專家權重聚類的權重優選法等方法確定[19].

綜上所述，本文研究的建設工程項目多資源均衡優化模型可定義為：

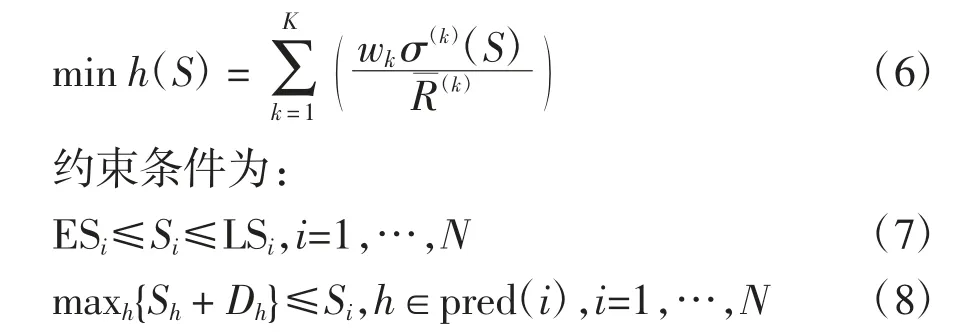
2 采用間隔率變量表示的建設工程項目多資源均衡優化模型

針對資源均衡問題的優化算法中，各工序計劃開始時間（優化問題的設計變量）通常直接在其最早開始時間和最晚開始時間之間取值，即ESi≤Si≤LSi，i=1，…，N.但是，這種設計變量的取值方式，容易違反工序間的邏輯關系（不滿足公式（8）對應的約束條件），需要引入復雜的修復算子來調整設計變量的取值.考慮圖2 所示的簡單建設工程項目的單代號網絡圖，圖中標明了各工序的持續時間、最早開始時間、及最晚開始時間.由圖2 可知，該網絡中的非關鍵工序為工序2 和工序4.如直接在工序最早開始時間和最晚開始時間之間取值，工序2 和工序4 的計劃開始時間可以分別取7 和8，但這樣的取值顯然違反工序2 與工序4 的邏輯關系.具體而言，因工序2為工序4 的緊前工序，在工序2 的計劃開始時間為7的條件下，工序4 的最早開始時間變更為9，其計劃開始時間不能取8.

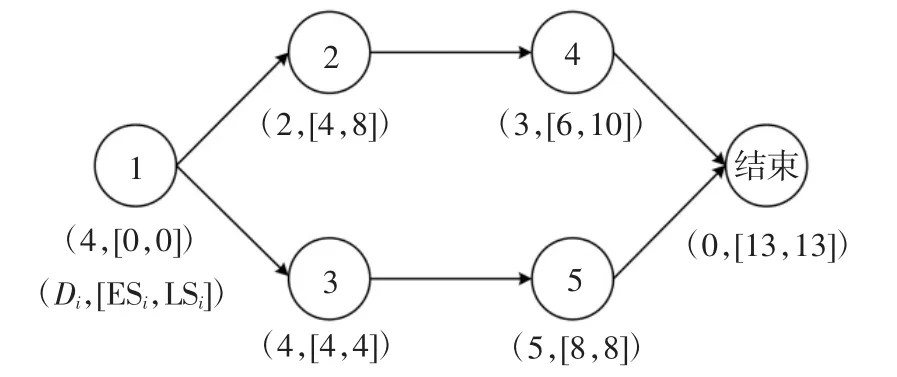
圖2 典型建設工程項目的單代號網絡圖Fig.2 Activity-on-node network of a typical construction project

為避免上述取值方式的問題，本文采用文獻[16]中提出的工序計劃開始時間的間隔率表示方法.具體而言，考慮到LSi≤maxh{Sh+Dh}，h∈pred（i），可將公式（7）和（8）對應的約束條件合并，即工序i 的計劃開始時間Si取值范圍為：

如將區間[0，1]等分為（LSi-max{Sh+Dh}+1）個子區間，則這些子區間與Si可取的（LSi-max{Sh+Dh}+1）個整數間存在一一對應的關系.因此，可定義在區間[0，1]連續取值的變量xi（間隔率變量），并根據其所在子區間，映射到工序i 的計劃開始時間Si，

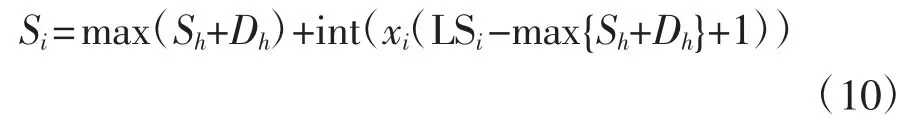
式中：int（）為取整函數.針對圖2 所示的簡單項目，如工序2 和工序4 的間隔率變量分別取0.73 和0.14，利用公式（10）可求得相應的計劃開始時間分別為4+int（0.73×（8-4+1））=7 和9+int（0.14×（10-9+1））=9.顯然可見，通過工序計劃開始時間的間隔率變量表示，可避免違背工序間的邏輯關系.

利用間隔率變量和計劃開始時間之間的映射（公式（10）），原始的離散變量優化問題（公式（6）～（8））可轉化為如下的連續變量優化問題：

約束條件為：

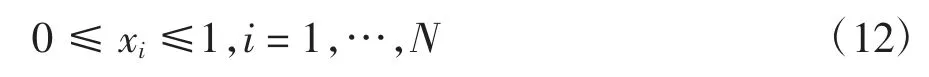
式中：g（x）為間隔率變量x=[x1，x1，…，xN]對應的目標函數.為計算目標函數值g（x），可首先利用公式（10）計算給定x 對應的各工序的計劃開始時間S=[S1，S2，…，SN]，進而代入原始優化問題的目標函數h（S）（公式（6））.

3 基于子集模擬的多資源均衡優化算法

子集模擬法（Subset Simulation）是Au 和Beck 提出的、針對結構可靠度問題的高效數值模擬算法[20].其思想是通過引入一系列中間失效事件，將偶發事件的小概率估計問題轉化為一組較大的條件概率估計問題，進而提高數值模擬算法的計算效率.通過建立可靠度問題和優化問題的內在聯系，子集模擬法也在優化設計問題中取得了較好的應用[21-22].

3.1 基于子集模擬的多資源均衡優化框架

考慮如下的全局優化問題：

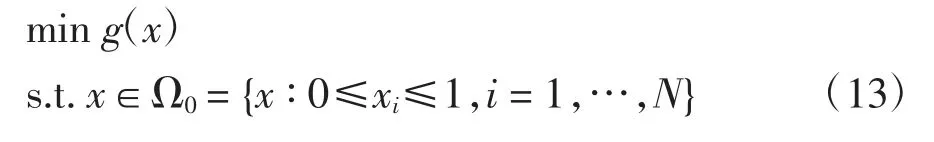
為利用子集模擬法求解上述優化問題，人為設定設計變量x 為隨機變量，服從可行域Ω0={x ∶0≤xi≤1，i=1，…，N}內的均勻分布.此外，子集模擬法通過引入一系列遞減的邊界值g1＞g2＞…＞gJ，在可行域Ω0內定義一系列逐漸收縮的區域Ωj={x ∶x∈Ω0，g（x）≤gj}，j=1，…，J.其中，每一區域為之前區域的子集，即Ω0?Ω1?Ω2…?ΩJ.通過依次在可行域Ω0及逐漸收縮區域Ωj（j=1，…，J）內按均勻分布進行隨機取樣，子集模擬法可逐漸縮窄搜索區域，最終在最優解附近的較小區域進行搜索，以得到問題的最優解.

基于子集模擬的優化算法有兩個重要參數：在指定區域中抽樣的樣本數量M 及條件概率參數p0.參數M 和p0的選擇，需確保Mp0和1/p0均為正整數.由于Mp0確定了每一迭代中收縮區域初始樣本點的數量，當p0過小時，需要較大的樣本數量M 才能保證Mp0的數值不至過小，以達到對收縮區域的有效搜索.當p0過大時，迭代中考察區域的收縮變慢，優化算法需要較多的迭代次數.綜合目前的研究成果，p0一般在0.05～0.3 區間取值，進而根據可承受計算資源確定樣本數量M.在參數確定后，基于子集模擬的優化算法首先在可行域Ω0內，產生服從均勻分布的M 個設計變量樣本，并計算它們的目標函數值.接著，將目標函數值由小到大排序，并取排在第Mp0位置的目標函數值作為定義區域Ω1={x ∶x∈Ω0，g（x）≤g1}的邊界值g.此時，之前產生的M 個設計變量樣本（服從可行域Ω0內的均勻分布）中，有Mp0個落在定義的收縮區域Ω1內（服從收縮區域Ω1內的均勻分布）.因此，可采用馬爾科夫鏈蒙特卡羅模擬方法（Markov chain Monte Carlo simulation，MCMCS，詳見3.2 節），以這Mp0個設計變量樣本作為Mp0個鏈條的起點，并針對每一鏈條額外產生（1/p0-1）個狀態點，以產生區域Ω1內服從均勻分布的M 個設計變量樣本

圖3～圖6 描述了參數M=20 和p0=0.2 時的上述流程.針對圖3 可行域Ω0內服從均勻分布的20個設計變量樣本，圖4 給出了它們所對應的目標函數值的升序排列.此時，定義下一收縮區域Ω1的邊界值g1，由20 個目標函數值中第Mp0=4 小的數值確定，見圖4.對應上述確定的g1，之前可行域Ω0內均勻分布的M=20 個設計變量樣本，有Mp0=4 個落在收縮區域Ω1={x ∶x∈Ω0，g（x）≤g1}內，見圖5.為產生收縮區域Ω1內均勻分布的M=20 個設計變量樣本，可采用MCMCS 方法，以目前的Mp0=4 個樣本為種子，分別產生4 條馬爾科夫鏈鏈條，見圖6.每條鏈條以其中一個種子為起點，額外產生（1/p0-1）=4 個狀態點，以確保總的樣本數為Mp0（1/p0-1+1）=M=20.

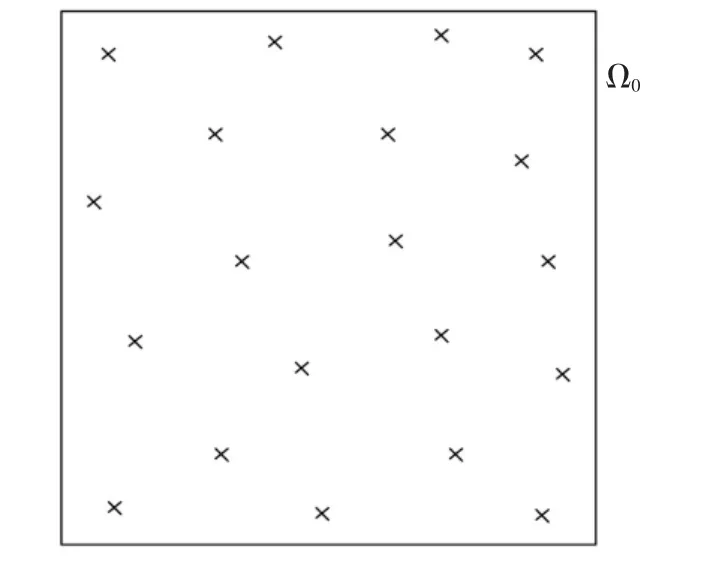
圖3 可行域Ω0 內均勻分布的設計變量樣本點（M=20）Fig.3 Samples of the vector of design variables uniformly distributed in the feasible region Ω0（M=20）

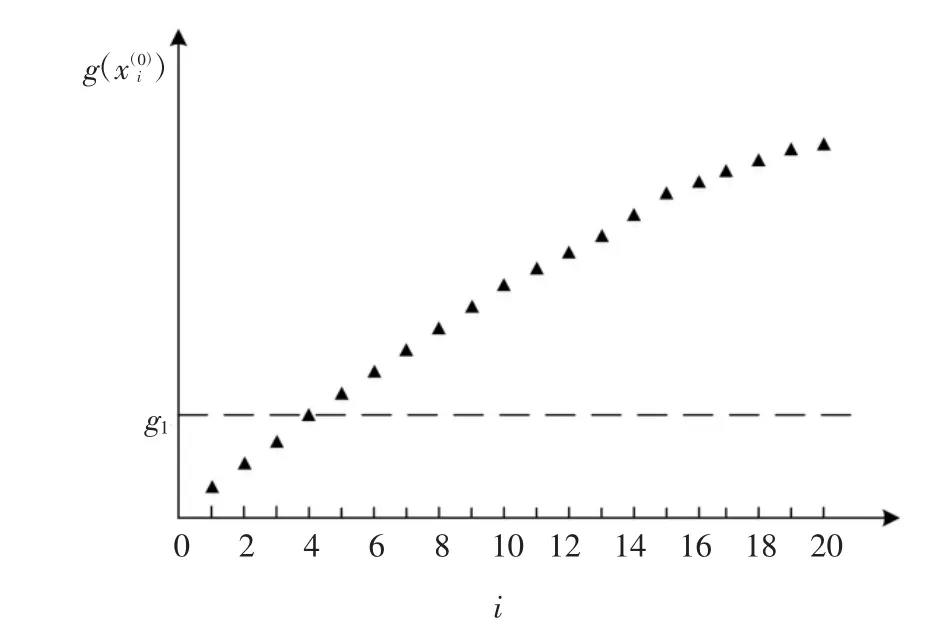
圖4 定義收縮區域Ω1 的邊界值g1（M=20，p0=0.2）Fig.4 Threshold value of g1 for the shrinking region of Ω1（M=20，p0=0.2）

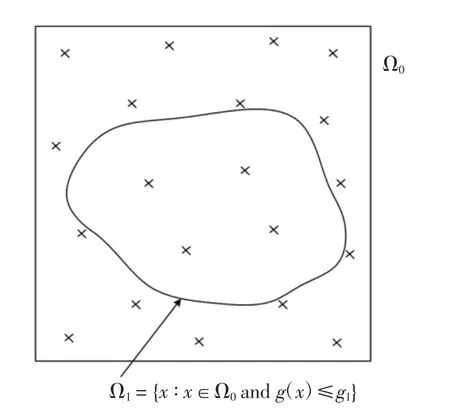
圖5 收縮區域Ω1 及落入其中的初始樣本點（M=20，p0=0.2）Fig.5 Shrinking region of Ω1 and the seed samples in Ω1（M=20，p0=0.2）

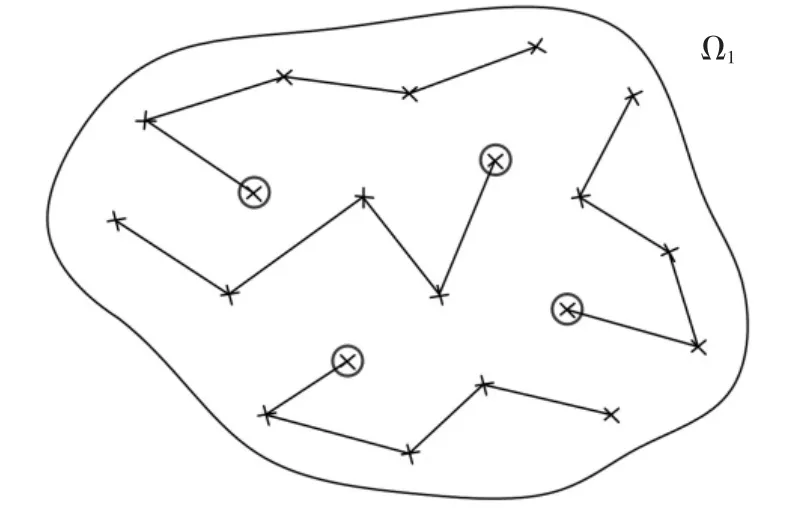
圖6 區域Ω1 內均勻分布的設計變量樣本點Fig.6 Samples uniformly distributed in Ω1

得到區域Ω1內服從均勻分布的M 個設計變量樣本后，可依次迭代重復上述邊界值的確定和對應收縮區域內隨機樣本點的產生流程，直到優化算法的迭代終止原則滿足為止.此時，選擇最終的收縮區域中隨機樣本點的最優者作為問題的最優解.

3.2 收縮區域Ωj={x ∶x∈Ω0，g（x）≤gj}內均勻分布樣本點的產生

如3.1 節所述，基于子集模擬的多資源均衡優化算法中，需根據收縮區域Ωj內均勻分布的少量樣本點，利用MCMCS 方法產生滿足要求數量的樣本點.考慮到多資源均衡優化問題中設計變量的維數（對應項目涉及的工序數量）可能較大，本文采用改進Metropolis-Hasting 方法[20]完成馬爾科夫鏈的產生任務.

采用p*（ξ/x）來表示以x 為中心點，以d 為寬度（即x-d/2 ≤ξ ≤x+d/2）的一維均勻分布的概率密度分布函數，d 一般可取0.2～0.4.該概率密度分布函數自動滿足對稱性，即p*（ξ/x）=p*（x/ξ）.為產生給定樣本點x1為起點的馬爾科夫鏈{x1，x2，…}，本文利用改進Metropolis-Hasting 方法的思想，采用如下xk=[xk（1），xk（2），…，xk（N）]到xk+1=[xk+1（1），xk+1（2），…，xk+1（N）]的迭代操作：

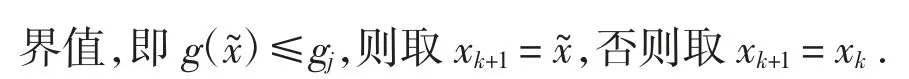
3.3 基于子集模擬的多資源均衡優化算法總結

針對采用間隔率變量表示的建設工程項目多資源均衡優化模型（公式（11）～（12）），本文基于子集模擬法，建議的優化算法步驟總結如下：

1）確定子集模擬算法中采用的參數，即在指定區域中抽樣的樣本數量M、條件概率參數p0和改進Metropolis-Hasting 方法中定義一維均勻概率分布的寬度d.

4）算法采用的迭代終止原則為達到預先設定的迭代次數J.如不滿足迭代終止條件，即j ＜J，令j=j+1，重復步驟3.

4 算例分析

本文采用30 個工序組成的建設工程項目算例，來檢驗基于子集模擬的多資源均衡優化算法的性能.基于標準算例庫PSPLIB（Project Scheduling Problem Library）[23]中算例j301_1 的數據，表1 給出了算例項目的具體信息，包括項目中各工序的緊前工序（第3 列）、各工序的持續時間（第4 列），各工序每天對應需求的4 種資源（人工、水泥、碎石、自卸車）的消耗量（第5～8 列）.根據各工序的持續時間和工序間的邏輯關系，可計算出該建設工程項目的工期為T=38 d.因標準算例庫在模型構建方面的信息并不充分，沒有提供項目管理專家所需的針對權重指標判斷的有效信息.因此，各資源的相對權重選擇確定為[w1，w2，w3，w4]=[0.2，0.2，0.4，0.2]，如項目的信息足夠，需采用專家判斷法確定.

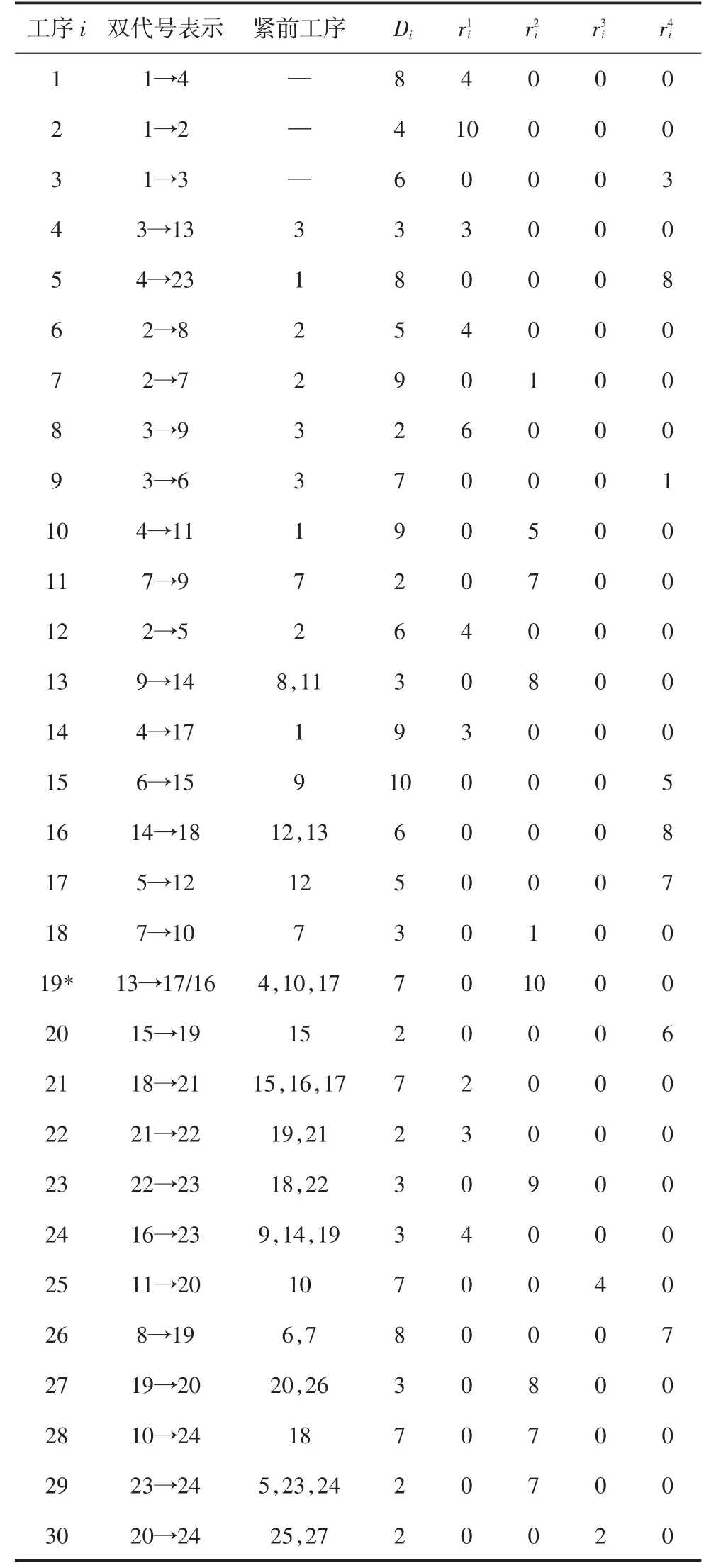
表1 算例數據Tab.1 Data of the example

為檢驗基于子集模擬的多資源均衡優化算法的性能，每代隨機抽樣樣本數量取M=2 000，條件概率參數取p0=0.1，改進Metropolis-Hasting 方法中一維均勻概率分布的寬度取d=0.3.圖7 描述了基于子集模擬的建議優化算法一次典型求解過程中，最優目標函數值隨迭代階段的變化.由圖7 可知，算法經過19 代迭代后收斂到最優解，對應最優目標函數值1.115 4.該最優解對應的各工序計劃開工時間Si如表2 所示.為直觀對比優化前后各工序的開工時間，圖8 和圖9 繪制了優化前后的雙代號時標網絡圖，各工序在圖中的雙代號表示見表1 第2 列.

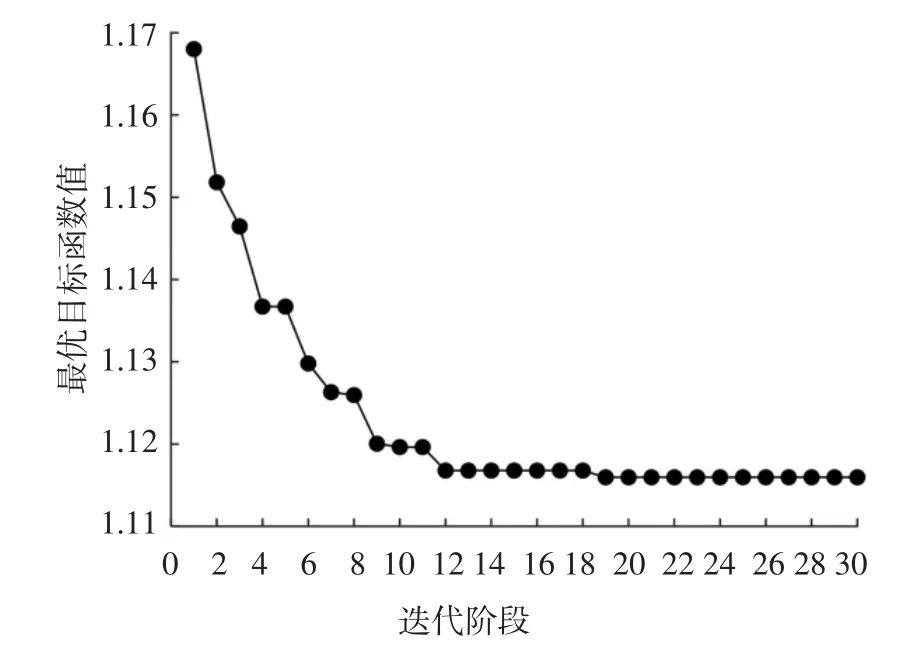
圖7 最優目標函數值隨迭代階段的變化Fig.7 Optimal objective function value at different stages

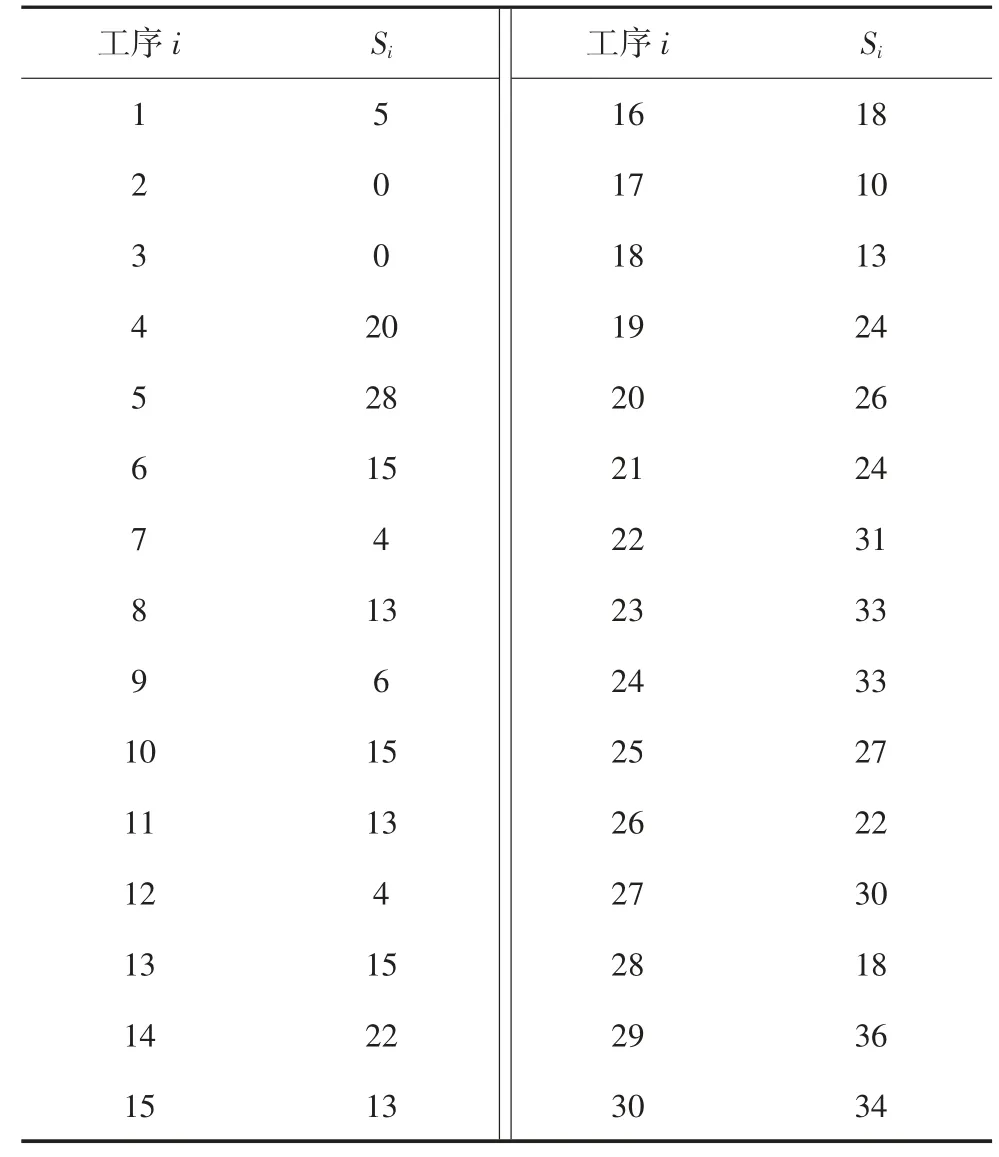
表2 典型最優解對應的工序計劃開工時間Tab.2 Scheduling time for the activities corresponding to the optimal solution

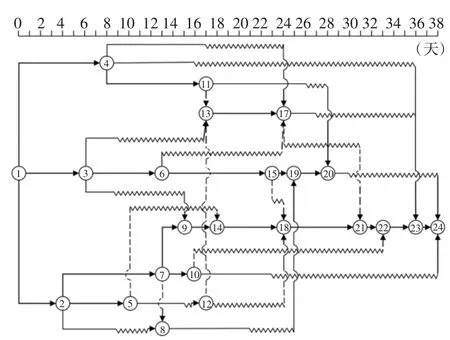
圖8 優化前算例的雙代號時標網絡圖Fig.8 The activity-on-arc time scaled network before optimization

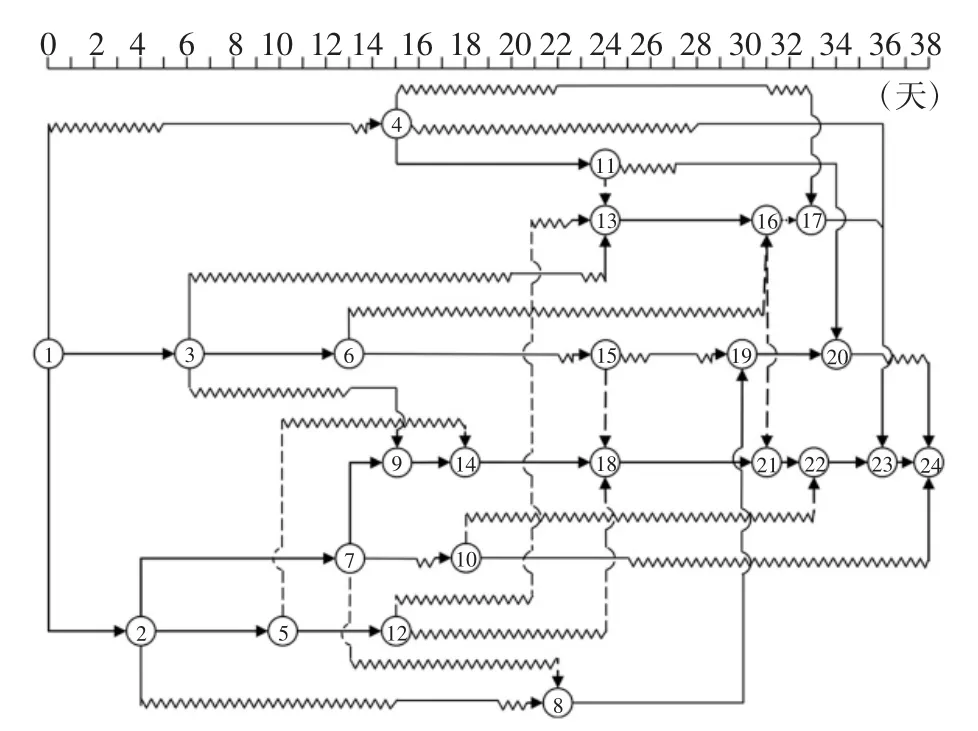
圖9 優化后算例的雙代號時標網絡圖Fig.9 The activity-on-arc time scaled network after optimization

為檢驗基于子集模擬的建議優化算法的穩定性，表3 給出了建議優化算法100 次獨立運行求解后的統計結果.目前，針對資源均衡問題的啟發式算法間的對比研究較少，學界對各種啟發式算法的優劣未達成共識.同時，遺傳算法因其自行概率搜索、運算并行性、應用不依賴問題種類的強魯棒性等特點，在資源均衡問題中應用更為廣泛[16-18].因此，本文選擇遺傳算法進行對比分析，與其他啟發式算法的對比分析，將在后續的研究中進行.表3 提供了遺傳算法（Genetic Algorithm，GA）100 次獨立運行求解后的統計結果.考慮到交叉概率參數pc和變異概率參數pm對GA 算法求解的影響，本文依據兩個參數的一般取值范圍，進行了大量pc和pm組合取值下GA 算法的性能檢驗.檢驗發現，交叉概率pc=0.2 和變異概率pm=0.015 下GA 算法求解本算例多資源均衡問題的性能最優，因此表3 給出的是這組交叉概率和變異概率下GA 算法的對比結果.同時，考慮到計算資源對兩種優化算法的影響，兩種優化算法中每代的樣本數均取2 000，迭代次數均取30 代.

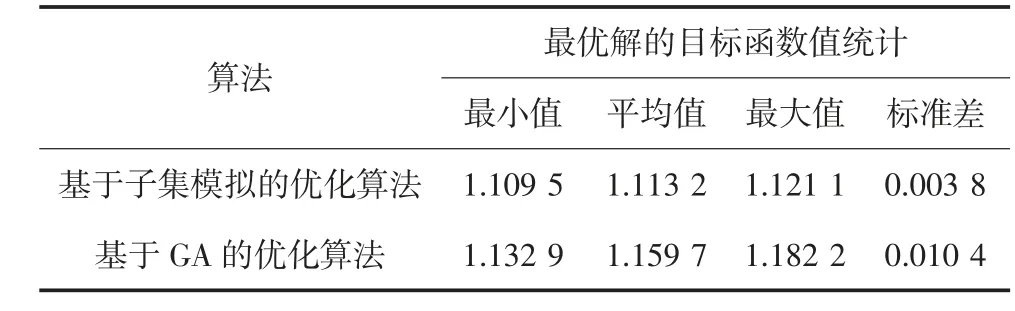
表3 基于子集模擬的優化算法與GA 算法獨立運行100 次獲得的最優目標函數值的統計結果Tab.3 Statistical results of 100 independent runs using subset simulation-based proposed algorithm and GA

表3 提供了兩種算法100 次獨立運行求解獲得的最優解的目標函數值的統計結果（最小值、平均值、最大值及標準差）.對比可知，基于子集模擬的優化算法獲得最優目標函數值的平均值為1.113 2，小于基于GA 的優化算法的相應數值（1.159 7）.同時，基于子集模擬的優化算法獲得最優解的目標函數值的最大值（最差情況下）為1.121 1，小于基于GA 的優化算法獲得最優解的目標函數值的最小值（最好情況下）1.132 9，且最優目標函數值的標準差更小.此外，圖10 給出了兩種算法100 次獨立運行獲得的最優解的目標函數值的分布情況.由圖10 可見，基于子集模擬的優化算法性能更優，其獲得的最優目標函數值更小，且分布更為集中，有93%的最優目標函數值集中在[1.109，1.119]區間，表明基于子集模擬的建議優化算法獲取最優解的穩定性更高.

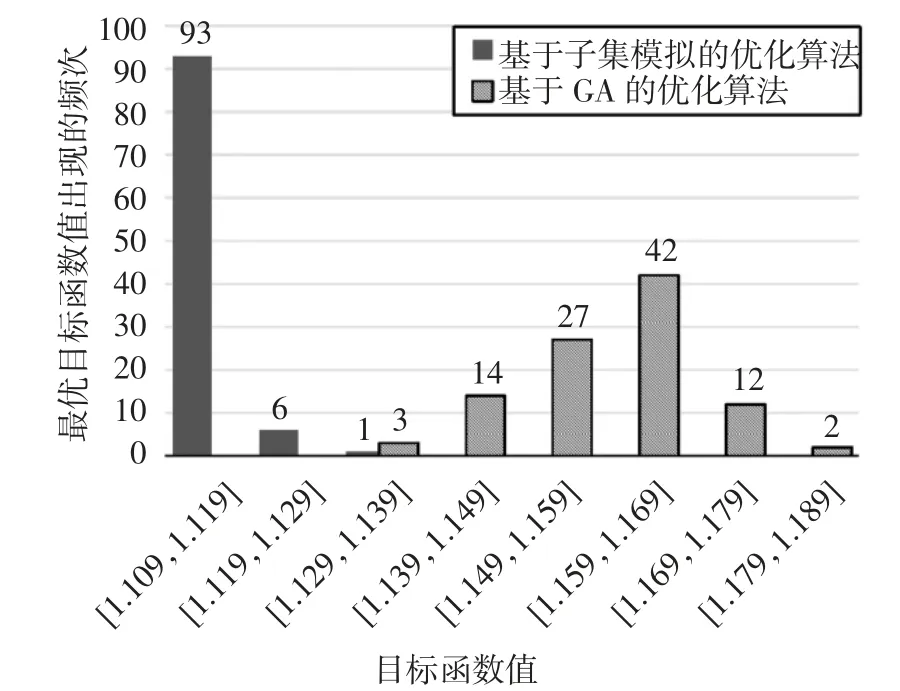
圖10 兩種優化算法獨立運行100 次獲得的最優目標函數值的分布Fig.10 Distribution of the optimal objective function value from 100 independent runs of using subset simulation-based proposed algorithm and GA

5 結論

本文針對建設工程項目的多資源均衡優化問題，基于子集模擬法進行啟發式優化算法的研究，主要研究結論如下：

1）在構造建設工程項目多資源均衡優化模型時，引入間隔率變量，并在間隔率變量和工序計劃開始時間的映射中考慮工序間邏輯關系，以避免工序邏輯關系違反時復雜修復算子的使用.

2）針對間隔率變量表示的建設工程項目多資源均衡優化模型，提出基于子集模擬的建議優化算法，并給出算法框架和具體操作步驟.

3）通過算例驗證，與應用較廣的遺傳算法相比，基于子集模擬的建議優化算法在最優解的獲取穩定性上有較大改進.