基于PCA-RF直流爐中間點(diǎn)溫度預(yù)測控制

梁偉平，鮑鵬凱

（華北電力大學(xué) 控制與計(jì)算機(jī)工程學(xué)院，河北 保定 071003）

0 引言

為了加快潔凈燃煤發(fā)電新技術(shù)的研發(fā)和推廣應(yīng)用，提高煤電發(fā)電效率及節(jié)能環(huán)保水平，在未來的很多年，煤炭在中國能源結(jié)構(gòu)中的主導(dǎo)地位不會發(fā)生根本的改變。由于未來全球能源需求預(yù)計(jì)仍將大幅增加，國際能源署煤炭產(chǎn)業(yè)咨詢委員會強(qiáng)調(diào)指出，煤炭將繼續(xù)作為21世紀(jì)的全球能源解決方案[1]。為了響應(yīng)節(jié)約資源的號召，大機(jī)組、大容量、大電網(wǎng)的電力系統(tǒng)已經(jīng)開始逐漸取代了過去的小機(jī)組、小容量的電力生產(chǎn)潮流，而直流鍋爐作為現(xiàn)代電力生產(chǎn)的主要設(shè)備，承載著節(jié)約資源和保護(hù)環(huán)境的作用，而分離器出口溫度作為反應(yīng)直流鍋爐中給水流量和水煤比的一個重要的工況指標(biāo)，它直接關(guān)系著機(jī)組的安全運(yùn)行，研究它對電力生產(chǎn)過程的重要性不言而喻。

直流鍋爐中間點(diǎn)溫度一般是汽水分離器出口的飽和溫度。目前，國內(nèi)的許多學(xué)者針對它開展了一系列的研究。羅志浩[2]等人在典型直流爐中間點(diǎn)溫度控制特點(diǎn)的研究中，指出直流鍋爐的中間點(diǎn)溫度過熱度對機(jī)組過熱汽溫、水冷壁和過熱器金屬溫度都十分敏感，中間點(diǎn)溫度過熱度控制的品質(zhì)直接關(guān)系機(jī)組的穩(wěn)定安全運(yùn)行。方彥君[3]等在基于主蒸汽溫度控制系統(tǒng)，建立了鍋爐水冷壁部分的物理模型，根據(jù)守恒定律，測試了其在不同運(yùn)行工況下的中間點(diǎn)溫度機(jī)理模型的性能。袁淑娟[4]等以超臨界直流鍋爐為研究對象，分析了給水量和燃料量與鍋爐中間點(diǎn)溫度的關(guān)系，建立了中間點(diǎn)溫度非線性離散模型，并進(jìn)行控制系統(tǒng)設(shè)計(jì)，證明了該控制系統(tǒng)在適應(yīng)變工況運(yùn)行的同時，能夠?qū)崿F(xiàn)中間點(diǎn)溫度穩(wěn)定的控制目的，能實(shí)時響應(yīng)負(fù)荷變化。鐘治琨[5]從鍋爐的分布參數(shù)和多變量密切耦合的特性角度為出發(fā)點(diǎn)，建立了自我組織的模糊神經(jīng)網(wǎng)絡(luò)的方法來模擬中間點(diǎn)溫度控制系統(tǒng)，并且在水煤比發(fā)生變化的情況下很好地反映了中間點(diǎn)的溫度動態(tài)。

上述文獻(xiàn)雖有對中間點(diǎn)溫度的研究，但是他們只注重從機(jī)理方面研究中間點(diǎn)溫度與各種鍋爐工況之間的聯(lián)系，并沒有實(shí)際地去研究如何去預(yù)測中間點(diǎn)溫度的值。本文采集了某電廠DCS歷史數(shù)據(jù)，建立了基于PCA降維技術(shù)的隨機(jī)森林模型，并通過仿真實(shí)驗(yàn)驗(yàn)證了模型的有效性。

1 預(yù)測模型介紹

1.1 PCA降維技術(shù)的原理

所謂的數(shù)據(jù)降維是對原始的高維特征數(shù)據(jù)進(jìn)行映射，有選擇地得到一些重要的特征，實(shí)現(xiàn)數(shù)據(jù)從高維到低維的轉(zhuǎn)化。常見的降維方法有：獨(dú)立成分分析（ICA）[6]、奇異值分解（SVD）[7]、因子分析法[8]、等距特征映射（ISOMAP）[9]。

本文采用的PCA（主成分分析）是一種線性組合的算法，用少數(shù)新變量去代替原來變量，使得到降維后的新特征盡可能多地去包含原來特征的信息，去除原來特征中重復(fù)的一部分信息。

假設(shè)數(shù)據(jù)樣本集中的樣本數(shù)有m個，其中單個樣本的維度是n維。

其實(shí)現(xiàn)步驟如下：

2）計(jì)算樣本的協(xié)方差矩陣：

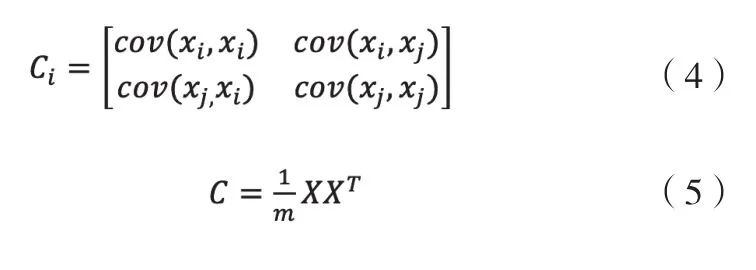
3）求協(xié)方差矩陣C的特征值和相對應(yīng)的特征向量

根據(jù)式（6）求協(xié)方差矩陣的特征值和特征向量：

讓計(jì)算好的λ從大到小進(jìn)行排列，將得到的特征向量按λ的順序進(jìn)行排列。

4）通過3）得到特征向量組成的矩陣，利用其對原始數(shù)據(jù)進(jìn)行降維操作，得到降維后的新數(shù)據(jù)集：

5）通過4）得到的新的數(shù)據(jù)集，然后一一計(jì)算其所包含某個特征的信息貢獻(xiàn)率和累計(jì)信息貢獻(xiàn)率。

信息貢獻(xiàn)率計(jì)算公式如下：

前k個特征的累計(jì)方差貢獻(xiàn)率如下：

根據(jù)公式（9）計(jì)算得到的累計(jì)方差貢獻(xiàn)率總和，當(dāng)其貢獻(xiàn)值達(dá)到90%以上時，就選擇它所包含的部分特征代替原來的幾個特征進(jìn)行分析。

1.2 隨機(jī)森林RF模型的構(gòu)建

隨機(jī)森林算法最早是由美國統(tǒng)計(jì)學(xué)家Leo Breiman[10]在2001年提出的，他將Bagging集成學(xué)習(xí)理論[11]與隨機(jī)子空間方法[12]相結(jié)合，提出一種機(jī)器學(xué)習(xí)算法。RF是以決策樹為基本分類器的一個集成學(xué)習(xí)模型。集成學(xué)習(xí)是將單個分類器聚集起來，通過對每個基本分類器的分類結(jié)果進(jìn)行組合，來決定待分類樣本的歸屬類別[13]。其模型示意圖如圖1所示。

圖1 隨機(jī)森林模型示意圖Fig.1 Schematic diagram of random forest model

隨機(jī)森林模型構(gòu)建步驟如下：

不防設(shè)樣本的特征個數(shù)為n，其中m為n的子特征（0＜m ≤ n）。

1）利用隨機(jī)森林中重采樣方法（Bootstrap），從原始數(shù)據(jù)集中進(jìn)行有放回的采樣，生成一個樣本數(shù)為T的訓(xùn)練集 ：b1,b2,b3,......,bT。

2）利用第1步得到訓(xùn)練集，生成與其對應(yīng)的決策樹：T1,T2,......Tn，在其生成的對應(yīng)的決策樹的非葉子節(jié)點(diǎn)上選擇特征前，從n個特征中隨機(jī)抽取m個特征作為分裂的起始點(diǎn)，并且以這m中最好的生長方向?yàn)榉至训淖罴逊较颉?/p>

3）在第2步完成以后，讓得到的決策樹都自由地生長，生長結(jié)束以后傳入樣本的測試集X，利用生長好的決策樹一一進(jìn)行測試，得到相應(yīng)的類別。

4）將第3步得到的決策樹采用投票的方法，把其中輸出最多的作為其類別。

1.3 PCA-隨機(jī)森林架構(gòu)（見圖2）

圖2 PCA-隨機(jī)森林架構(gòu)Fig.2 PCA Random forest architecture

2 對實(shí)驗(yàn)數(shù)據(jù)進(jìn)行處理

本實(shí)驗(yàn)采用的數(shù)據(jù)來源于華北地區(qū)某電場，數(shù)據(jù)采集是通過DCS系統(tǒng)導(dǎo)出來的實(shí)測數(shù)據(jù)，測量的數(shù)據(jù)種類包括：燃料量、給水流量、三級過熱器出口煙氣溫度1、三級過熱蒸汽煙氣溫度2、主蒸汽壓力、主蒸汽溫度、中間點(diǎn)溫度。其中，這些采集到的數(shù)據(jù)都是帶雙引號的文本格式，不能直接根據(jù)需要對其進(jìn)行處理，得到正常的計(jì)算機(jī)可以識別的格式。

由于采集的數(shù)據(jù)量綱不一樣，量綱的不同會導(dǎo)致計(jì)算結(jié)果的不同，尺度大的特征在計(jì)算中往往起決定作用，而尺度小的特征在計(jì)算中往往會被忽略。因此，為了消除特征尺度的差異，所以需要對其數(shù)據(jù)做歸一化處理。其歸一化公式如式（10）所示：

對采集的數(shù)據(jù)處理完成后，如果直接選用8個影響因素建立預(yù)測模型，容易導(dǎo)致模型訓(xùn)練時出現(xiàn)過擬合。因此，需要通過PCA算法刪除樣本中冗余的部分，采用PCA進(jìn)行分析，將其分析得到的貢獻(xiàn)率利用排序工具讓其從大到小進(jìn)行排序，如圖3所示。

圖3 各主成分的貢獻(xiàn)率Fig.3 Contribution rate of principal components

從圖3和表1可以看出，前3個特征的累積方差貢獻(xiàn)率達(dá)到了95%，可以用前2個特征來代替原始數(shù)據(jù)集，用BP神經(jīng)網(wǎng)絡(luò)和隨機(jī)森林對降維后的數(shù)據(jù)進(jìn)行訓(xùn)練和預(yù)測。

表1 各主成分貢獻(xiàn)率的值Table 1 Values of contribution rate of principal components

3 預(yù)測結(jié)果與分析

通過PCA降維技術(shù)選用燃料量、給水流量兩個特征和選用數(shù)據(jù)集的前1900個數(shù)據(jù)組成原始數(shù)據(jù)集，對RF（隨機(jī)森林）和BP神經(jīng)網(wǎng)絡(luò)進(jìn)行訓(xùn)練和預(yù)測。其中，BP神經(jīng)網(wǎng)絡(luò)的訓(xùn)練模型參數(shù)設(shè)定見表2。

表2 BP神經(jīng)網(wǎng)絡(luò)的參數(shù)設(shè)定Table 2 Parameter setting of BP neural network

從圖4、圖5和表3可知，在一定的誤差范圍內(nèi)，即417＜range＜419.5時，在100個樣本中，PCA-BP的預(yù)測個數(shù)為51個，PCA-RF的個數(shù)為78個，通過公式：

圖4 BP神經(jīng)網(wǎng)絡(luò)的預(yù)測結(jié)果Fig.4 Prediction results of BP neural network

圖5 PCA-RF的預(yù)測結(jié)果Fig.5 Prediction results of PCA-RF

表3 在一定的誤差下預(yù)測正確率Table 3 Prediction accuracy under certain error

基于PCA降維算法隨機(jī)森林的正確率大于基于PCA降維算法的BP神經(jīng)網(wǎng)絡(luò)的正確率，且是預(yù)測正確的樣本里其單個元素的誤差大部分都小于BP神經(jīng)網(wǎng)絡(luò)正確樣本的單個元素。同時比沒有采用PCA降維算法的隨機(jī)森林相比，運(yùn)行時間提高了0.2 s。

4 結(jié)論

為了實(shí)現(xiàn)對中間點(diǎn)溫度進(jìn)行有效的預(yù)測，本文提出了一種基于PCA-RF模型：

1）根據(jù)DCS系統(tǒng)采集的歷史數(shù)據(jù)，結(jié)合數(shù)據(jù)的特點(diǎn)引入了PCA降維算法，剔除了數(shù)據(jù)中影響較小的部分。

2）隨機(jī)森林與其它算法相比較，有著較好的擬合能力，可以對數(shù)據(jù)進(jìn)行預(yù)測。

3）通過仿真實(shí)驗(yàn)發(fā)現(xiàn)，該RF模型與BP神經(jīng)網(wǎng)絡(luò)相比較擬合能力有進(jìn)一步的提高，同時該模型的預(yù)測準(zhǔn)確率比BP神經(jīng)網(wǎng)絡(luò)有很大提高，進(jìn)一步說明該模型具有一定的應(yīng)用潛力。