海冰模式中融池參數化方案的伴隨模式參數估計

陸洋 王曉春

(南京信息工程大學海洋科學學院, 南京 210044)

提要 融池是影響北極海冰變化的重要因子。但在目前廣泛使用的海冰模式CICE6.0中, 融池模擬與觀測存在較大差異。CICE6.0中的CESM融池參數化方案可以計算融池覆蓋率與深度, 但其中的部分重要參數存在一定的經驗性, 影響了融池模擬。本研究為CICE6.0海冰模式的CESM融池參數化方案開發了伴隨模式, 利用CICE6.0海冰模式、融池伴隨模式和L-BFGS極小化算法, 使用一年冰及多年冰區域的MODIS衛星融池覆蓋率觀測數據, 對CESM參數化方案中的融池縱橫比參數進行了分時段分區的參數估計。結果表明: 使用伴隨模式可以有效地對融池參數進行估計; 得到的融池參數隨時空變化, 符合融池過程時空變化強烈的特征; 估計的參數值用于模擬, 減小了融池覆蓋率的模擬誤差, 與MODIS觀測更為一致。

0 引言

北極夏季, 海冰和冰上積雪開始融化形成融水, 融水在自身重力作用下沿著冰表面流動, 匯聚于冰表面低洼處形成大小融池。由于較高的反照率, 海冰可以反射大部分的入射短波輻射。海冰融化將會使得更多的熱量被極區吸收, 從而促使更多的海冰融化, 稱為“海冰-反照率”正反饋[1]。融池的反照率低于海冰, 融池的形成將降低海冰反照率, 增強正反饋, 起到加速海冰融化的作用。因此, 融池在極區氣候系統中起到重要作用, 使得其成為近年來氣候科學家關注的熱點。隨著北極海冰融化加劇[2], 一年冰比重顯著增加[3-4], 而一年冰平整的表面有利融池形成后在水平方向擴展。盡管缺乏長期觀測數據, 但一般認為, 由于一年冰的增加, 北極的融池覆蓋率正在增加[5]。可以預料, 融池將對未來北極地區的氣候產生更明顯的影響。因此, 融池及其在海冰模式中的參數化研究具有十分重要的意義。

由于北極地區自然環境的限制, 融池的現場觀測一直比較缺乏。融池覆蓋率(Melt Pond Fraction, MPF)、反照率是觀測的重點。北極海表面熱平衡收支觀測計劃(Surface Heat Budget of the Arctic Ocean, SHEBA)執行期間曾對海冰反照率進行了長時間連續觀測[6], 測量得到的融池反照率隨時間迅速變化, 變化范圍達到0.1～0.65, 這與融池自身的發展演化密切相關。Eicken等[7]基于觀測指出季節尺度融池發展存在4個大致的階段: (1)融池形成階段; (2)融水流失階段; (3)融池穩定擴展階段; (4)融池重新凍結階段。不同階段的融池行為和控制機制不同。衛星遙感為融池觀測提供了新的數據。2012年, R?sel等[8]利用MODIS(Moderate Resolution Imaging Spectroradiometer)光學傳感器反射率數據反演了融池覆蓋率, 提供了2000—2011年每年5—9月中8天一次的北極融池覆蓋率產品。近年來, 開始利用微波遙感對融池進行觀測[9-11], 但尚未發布產品。現場觀測和衛星觀測均表明, 融池過程具有明顯的時空變化特征, 海冰模式中的融池參數化需要考慮這種特征。

融池在海冰模式中的參數化是非常重要的研究課題。由于融池在空間及時間上的明顯變化,根據冰表面特征直接指定固定的冰面反照率的做法, 無法很好考慮融池, 可能造成較大的模擬偏差[6]。為在模式中對反照率進行符合實際的計算,需要發展融池模式, 將其納入海冰模式中。融池觀測為融池模式的發展奠定了基礎, 目前已有幾種復雜程度不同的融池模式用在海冰模式中。早期的融池模式[12-14]為一維模式或者二維模式, 往往與現有氣候系統模式中的海冰模式不匹配, 不能很好地納入海冰模式中。Holland等[15]提出了一個簡單的融池參數化方案, 該方案可以計算融水體積, 并根據給定的融池縱橫比(融池深度與覆蓋率之比)分配融水體積。CICE海冰模式(Los Alamos Sea Ice Model)采用了該方案并稱為CESM(Community Earth System Model)方案。Flocco等[16-17]基于海冰模式中的厚度分布函數(Ice Thickness Distribution, ITD)建立了更為復雜的融池方案, 考慮了冰面地形對融水分配的影響,利用海冰厚度來確定冰面地形。在該方案中, 融水產生后首先覆蓋最低的冰面, 然后覆蓋次低的冰面, 逐層累加。此外, 該方案還考慮了由于海冰微孔隙結構所導致的融池水滲流等過程。CICE引入該方案稱為地形方案(Topography Scheme,TOPO)。Hunke等[18]綜合了CESM方案和TOPO方案, 提出平整冰方案(Level Ice Scheme, LVL),利用CICE中已有的平整冰變量, 假定融池只能存在于平整冰上, 并且假定融池體積的變化存在縱橫比, 從而分配融水體積。王傳印等[19]結合觀測數據對三種方案在CICE5.0中的表現進行了較為詳細的對比研究, 認為CESM方案的融池凍結條件更為合理, 但存在多年冰上積雪不能完全融化、融池被低估的問題。

但是, 以上融池參數化方案均建立在一定的假設上, 由于對某些過程缺乏認識, 包含了一些不確定性較大的參數, 降低了海冰模式的準確性和可靠性[20]。對于這部分不確定參數, 一般可以通過敏感性試驗的方法來研究和減小其不確定性。但這種方法有很強的局限性, 一方面氣候系統是復雜系統, 存在大量反饋過程, 另一方面在待研究參數較多的情況下, 這種方法所需要的計算代價較為高昂[21]。伴隨模式(Adjoint Model,ADM)為融池參數化方案中參數的估計提供了另外一種可能性[22-23]。伴隨模式是原始非線性模式的切線性模式(Tangent Linear Model, TLM)的轉置, 利用伴隨模式進行一次積分可以得到模式結果對所有模式變量(包括邊界條件、初始條件和模式參數)的導數, 進而可以定量地對參數進行調整。伴隨模式已經廣泛用于模式參數估計和初始場估計中。比如, Liu等[24]利用MITgcm(Massachusetts Institute of Technology General Circulation Model)海冰-海洋耦合模式及其伴隨模式進行了海冰模式中海冰密集度初始場優化的研究,得到的海冰密集度初始場和實際更接近, 說明伴隨模式可以用于對海冰模式初始場進行調整。Fenty等[22]利用MITgcm及其伴隨模式進行了2004年海冰-海洋耦合狀態估計, 同化了海洋水文資料和海冰密集度資料, 相比未同化資料的試驗, 對海冰和海洋狀態的估計都更加準確。Kim等[23]利用CICE模式的伴隨模式對模式中21個熱力和動力學參數同時進行了敏感性分析, 并利用計算得到的梯度信息對參數進行了試驗性調整,驗證了伴隨方法在海冰參數估計和優化中的可行性。以上研究表明, 伴隨模式已經在海冰模式參數估計中得到了廣泛應用, 但是這些研究中很少考慮融池參數。由于融池過程對于海冰模式的重要性以及融池模式中存在許多不確定參數, 有必要利用伴隨模式考慮重要的融池參數, 并通過優化算法對其進行估計, 以減小海冰模式在融池模擬中的誤差。

CESM融池參數化方案的融池縱橫比參數是基于SHEBA一年冰觀測數據的經驗參數[25]。由于多年冰上融池傾向于在深度方向上增長, 和一年冰融池存在顯著不同, 這個固定值參數對整個北極海冰的適用性較低。因此, 本文的研究目標為通過伴隨模式方法, 估計海冰模式中CESM融池參數化方案的融池縱橫比參數, 以改善該融池方案對融池覆蓋率的模擬結果。第1節介紹本文所用的數據、CICE6.0海冰模式和CESM融池參數化方案。第2節介紹本文所構建的融池伴隨模式、L-BFGS極小化算法、伴隨模式參數估計算法以及利用控制試驗的模擬數據對參數估計算法的驗證結果。第3節針對多年冰及一年冰海域, 利用MODIS融池觀測數據作為觀測約束, 對融池參數進行最優估計, 并將其用于模擬, 檢驗其對融池模擬的影響。第4節為本文結論與討論。

1 數據、CICE6.0海冰模式及融池參數化方案

1.1 融池覆蓋率與海冰密集度觀測數據

MODIS融池覆蓋率數據為德國漢堡大學研發的產品[8], 下載自漢堡大學綜合氣候數據中心網站: http://icdc.zmaw.de。該數據時間跨度為2000—2011年, 每年5月9日—9月6日, 時間分辨率為8天一次。空間范圍為180°W～180°E、60°N～90°N, 空間分辨率為12.5km×12.5km。衛星數據和現場觀測驗證數據的均方根誤差(Root Mean Squared Error, RMSE)的范圍在3.8%～11.2%之間。MODIS是光學傳感器, 因此反演的融池覆蓋率中包含云層所引起的數據缺測。這些缺測主要發生在2000年、2001年、2002年和2007年的80°N以北區域。較小的缺測區域已經在數據發布前進行了插值, 但忽略了面積大于12.5 km2的區域[26]。

本文使用的海冰密集度數據為英國氣象局哈德萊中心(Met Office Hadley Centre)的海冰和海表面溫度數據集HadISST1[27]。HadISST1整合了來自歷史觀測和衛星觀測的海冰數據, 提供了自1871年開始, 空間分辨率為1°×1°的全球逐月海冰密集度。

1.2 CICE6.0海冰模式及ICEPACK模塊

本文使用的CICE6.0海冰模式由美國Los Alamos國家實驗室研發[28], 建立在海冰厚度分布函數[29]的基礎上, 是一個大尺度熱力-動力學模式,考慮了成脊等次網格尺度機械過程的影響[30]。模式中使用位移極點網格或者三極網格來處理北極點的奇點問題[31]。ICEPACK是CICE6.0的一個子模塊[32], 刻畫了海冰熱力學和生物地球化學等網格元內的垂向物理過程(Column Physics)。ICEPACK通過計算大氣-海冰邊界層和海洋-海冰邊界層的能量收支來更新冰的溫度, 并以此確定冰的增長或融化。本文使用CICE6.0為ICEPACK提供的單獨的驅動程序, 獨立運行ICEPACK來模擬單點(垂直柱)的海冰狀態變化。

海冰模式的大氣強迫數據使用基于日本氣象廳(Japan Meteorological Agency, JMA)55年再分析資料JRA-55的海洋-海冰模式大氣強迫數據集JRA55-do[33]。本文研究的時間段為2005年, 所用變量包括10米處的氣溫、10米處的比濕、10米處的風矢量、向下短波輻射、向下長波輻射和降水。JRA55-do數據的時間間隔為3 h, 本文中將其線性插值到1 h間隔, 以匹配ICEPACK的1 h的積分步長。

1.3 CESM融池參數化方案

CESM融池參數化方案是CICE6.0海冰模式中3個融池參數化方案之一, 和文獻[15]中的方案有一些微小的不同之處。它可以計算融池的覆蓋率與深度, 描述了融池從生成到凍結的過程。該方案的核心是建立了融池深度和覆蓋率之間的線性關系, 認為深度隨覆蓋率線性增長, 即:

式中,hp表示融池深度,δp為融池縱橫比,ap表示融池覆蓋率。在CESM方案的默認設置中δp為0.8。融池水來自于海冰融水、積雪融水和降雨:

其中為模式中第 個時間步的單位面積融池體積(m),ρi和ρs分別為冰和雪的密度(kg·m-3),ρw為融水的密度(kg·m-3),frain為降水率(kg·m-2·s-1),Δt為時間步長(s), Δhi和Δhs分別為在Δt內海冰頂層的融化量(m)和積雪的融化量(m)。部分融水會從海冰邊緣、冰上裂縫和海豹呼吸洞等流失入海,r為融水進入融池的比例:

其中ai為海冰密集度。CICE6.0中rmin和rmax的默認值分別為0.15和0.7。而在文獻[15]中, 該比例為:r=0.15+0.7ai。氣溫降低時, 融池逐漸重新凍結, 體積減小:

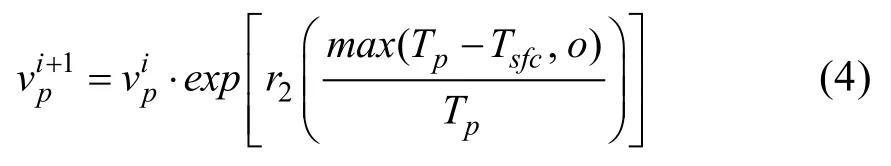
其中r2為系數0.01,Tp為參考溫度-2℃,Tsfc為海冰表面溫度(℃)。

2 融池伴隨模式及融池縱橫比參數估計算法

2.1 融池方案的伴隨模式及其驗證

本文為對融池模式中的參數進行估計, 研發了融池模式的伴隨模式。構造一個數值模式的伴隨模式有兩種路徑: 第一種路徑是基于解析的伴隨模式方程組離散得到伴隨模式, 第二種路徑是從原模式的代碼轉換得到。前者只適用于比較簡單的模式, 后者則可用于復雜模式。在第二種路徑中, 可以借助自動微分(Automatic Differential,AD)軟件工具來自動生成伴隨模式代碼[34], 這對于在設計之初考慮了數據同化問題并為之預先優化了代碼結構的模式(如MITgcm)是方便的。另外一些模式, 其伴隨模式需要直接轉換(人工逐行編寫伴隨模式代碼, 其遵循的編碼基本規范和自動微分軟件是相同的)得到, 如日本氣象廳氣象研究所(Meteorological Research Institute, MRI)的海冰模式伴隨模式[35]。本文所使用的CICE6.0模式并沒有為開發伴隨模式進行特別的代碼優化,無法使用自動微分工具生成伴隨模式[36]。因此,本文采用了直接轉換的方式, 這樣可以在一定程度上保證伴隨模式的正確性。

如1.3節所述, CESM融池方案在物理和數值計算上由4個部分組成: (1)首先計算由于冰雪的融化和降水所帶來的融水體積增量; (2)其次, 計算融水流失比例, 按比例扣除融水得到最終進入融池的融水體積增量; (3)根據氣溫和冰表面溫度,計算縮減后的融池水體積; (4)根據融池水體積,通過指定的融池縱橫比參數, 同時考慮海冰厚度對融池深度的限制, 計算融池覆蓋率和深度。根據這樣的特點, 本文開發伴隨模式的簡要步驟如下: 首先, 確定融池方案的輸入變量和輸出變量,選擇融池縱橫比δp作為輸入變量, 輸出變量為融池方案中依賴于δp參數的變量; 其次, 逐行線性化融池方案得到切線性模式; 最后, 將切線性模式算子轉置得到伴隨模式算子。本文伴隨模式中的基本態是重新計算的。對于模式中的分支結構語句(比如IF…ELSE…END)的處理方法是: 對兩個分支的語句分別進行線性化, 分支結構的判斷式若涉及輸入變量, 則用其基本態代替。對于融池方案的4個部分, 分別寫出伴隨代碼, 最終將計算順序顛倒組成完整的融池伴隨模式。伴隨模式編寫的具體規范和細節可以參考MM5伴隨模式系統的技術報告[37]。

得到的切線性模式和伴隨模式必須進行正確性檢驗才能使用。當擾動足夠小時, 由正向模式控制積分及其擾動積分計算得到的擾動大小應該和切線性模式計算結果非常接近。因此, 可以利用正向模式, 按下式來檢驗切線性模式的正確性:

其中,Q是正向模式,z是正向模式輸入變量向量,α為一尺度系數,h是輸入變量的擾動,代表從正向模式控制積分及其擾動積分的輸出所計算的擾動大小。P是切線性模式,Ph代表將h作為輸入運行切線性模式得到的擾動大小。在實際計算中,h應該足夠小, 使得可以忽略其高階項,同時應該大于機器舍入誤差。當尺度系數變小時,正向模式得到的擾動值與切線性模式得到的擾動值之比R趨向于1。

可以利用切線性模式, 按照下式檢驗伴隨模式的正確性:

其中,P是切線性模式,dz是切線性模式的輸入變量向量,PT是伴隨模式。將dz作為輸入, 運行切線性模式得到Pdz。將Pdz作為輸入, 運行伴隨模式PT得到PTPdz。＜＞表示向量內積。若上式在機器誤差精度內成立, 則伴隨模式代碼通過驗證。

按照公式( 5 )對切線性模式進行檢驗。其中尺度系數α從1.0減小到0.1, 擾動量h保持為0.2。結果如圖 1所示, 隨著α向0逼近,R逼近1, 說明切線性模式的代碼是正確的。按公式(6)對伴隨模式進行了檢驗, 其中dz=αh, 尺度系數α和擾動向量 的設置同切線性模式檢驗。伴隨模式檢驗結果如圖 2所示, 隨著α逼近0, 公式(6)兩邊之差的絕對值逐漸逼近0, 說明伴隨模式的代碼是正確的。

圖1 CESM融池切線性模式檢驗結果.α為擾動尺度系數, R(公式5)為正向模式積分得到的擾動大小與切線性模式積分得到的擾動大小的比Fig.1.Correctness check of CESM melt pond scheme tangent linear model.The α is a scaling factor.R (defined in Equation 5) is the ratio between the norm of perturbation from forward model integration and that from tangent linear model integration

圖2 CESM融池伴隨模式檢驗結果.α為擾動尺度系數,Δ(公式6兩邊之差的絕對值) 為切線性模式計算的擾動大小與伴隨模式計算的擾動大小之差的絕對值Fig.2.Correctness check of CESM melt pond scheme adjoint model.The α is a scaling factor.Δ (the norm of difference between the left-hand side and the right-hand side of Equation 6) is the difference between the perturbation from the tangent linear model and that from the adjoint model

2.2 L-BFGS極小化算法及目標函數

正向模式、伴隨模式和極小化算法的結合可以實現對模式參數的最優估計。本文中所使用的極小化算法為 L-BFGS算法(Limited-memory Broyden-Fletcher-Goldfarb-Shanno Algorithm), 它是一種擬牛頓法, 可以應用于大規模優化計算[38]。算法按照下述公式對被估計參數進行迭代:

其中,Xk為被估計參數的第k次迭代值,為第k次迭代的被估計參數目標函數的梯度, 可以通過伴隨模式給出,ρk為第k次迭代的步長, 由極小化算法自動調整。迭代終止條件為: (1)迭代次數大于2000次或者(2)達到指定精度, 滿足其中,為目標函數梯度的范數,ε的值在本文中設為10-5,為被估計參數的范數。

本文的研究目標為估計融池縱橫比參數, 減小融池覆蓋率模擬與觀測之間的誤差, 所以本文定義目標函數為:

其中,J為目標函數,為第i個觀測時間點MODIS觀測的融池覆蓋率,為對應第i個觀測時間點模式模擬的融池覆蓋率,N為觀測次數。目標函數J代表了模式和觀測之間的誤差, 當目標函數取得極小值時, 就得到了參數的估計。

2.3 海冰融池參數估計算法及其驗證

為了對融池參數進行參數估計, 需要構建一套有效的參數估計算法。該算法框架設計如下:第一步, 設定參數的初始估計值; 第二步, 進行正向模式積分, 得到融池的基本態, 將其保存,同時保存融池中間強迫數據以驅動融池伴隨模式,所謂融池中間強迫數據指作為融池模式輸入的5個海冰狀態參量(海冰頂層融化速率、積雪融化速率、海冰密集度、海冰體積和海冰表面溫度)和降水變量在模式積分中每一時間步的值; 第三步,將正向積分得到的融池覆蓋率數據與觀測數據根據公式(8)計算目標函數; 第四步, 利用融池中間強迫數據, 進行伴隨模式的反向積分, 得到伴隨變量的值; 第五步, 計算目標函數的梯度; 第六步, 將計算得到的目標函數值和梯度輸入LBFGS極小化算法, 極小化算法據此來自動調整最優步長及更新參數的估計值, 并判斷是否達到指定的迭代終止條件, 若達到條件, 則終止程序并返回最終的參數估計值, 反之則從第二步開始利用最新的參數估計值進行新的迭代循環。算法流程如圖 3所示。

圖3 融池參數估計算法流程圖Fig.3.Flow chart of the melt pond parameter estimation algorithm

驗證本文參數估計算法的方法和前人工作[39-41]相似, 采取了理想試驗的方式, 具體步驟為: 首先選取CICE6.0中的默認值0.8作為預先給定的δp參數值, 進行正向模式控制積分, 得到模擬的融池覆蓋率逐小時數據, 將此數據作為融池的“觀測”數據保存以供使用。然后設定參數的初始估計值為一隨機值0.7, 進行參數估計。檢驗伴隨模式及相應的極小化算法能否得到參數默認值0.8。

參數估計程序迭代了5次后結束, 得到的參數δp估計值為0.8。圖4a為參數δp在迭代過程中的變化。可以看到, 在迭代了2次之后參數估計值基本上接近預先設置的值0.8。圖4b顯示了目標函數J的值在迭代過程中的變化, 可以看出,目標函數在迭代前2步下降較快, 第2步已經接近零。圖4c為目標函數梯度范數在迭代過程中的變化, 這里目標函數梯度范數在兩次迭代后就變得非常接近于零, 表明目標函數將達到其極值。

圖4 參數估計中被估計δp參數 (a), 目標函數 (b) 和目標函數梯度范數 (c) 隨迭代次數的變化Fig.4.Change of the δp parameter (a), cost function (b) and norm of cost function gradient (c) with iteration number in parameter estimation process

為了檢驗初始估計值對參數估計結果的影響,進行了若干次試驗, 每次的初始估計值不同, 結果如表1所示。表1中第3列為參數的初始估計值, 從0.1變化到1.0。第4列為參數的最終估計值。從表中可以看出, 在不同初始估計值下, 參數估計算法都能得到“正確的參數估計值”0.8。同時, 迭代次數均在10次以下, 具有較高的計算效率。以上計算驗證了伴隨模式和參數估計的算法。結果表明, 參數估計算法是有效的。

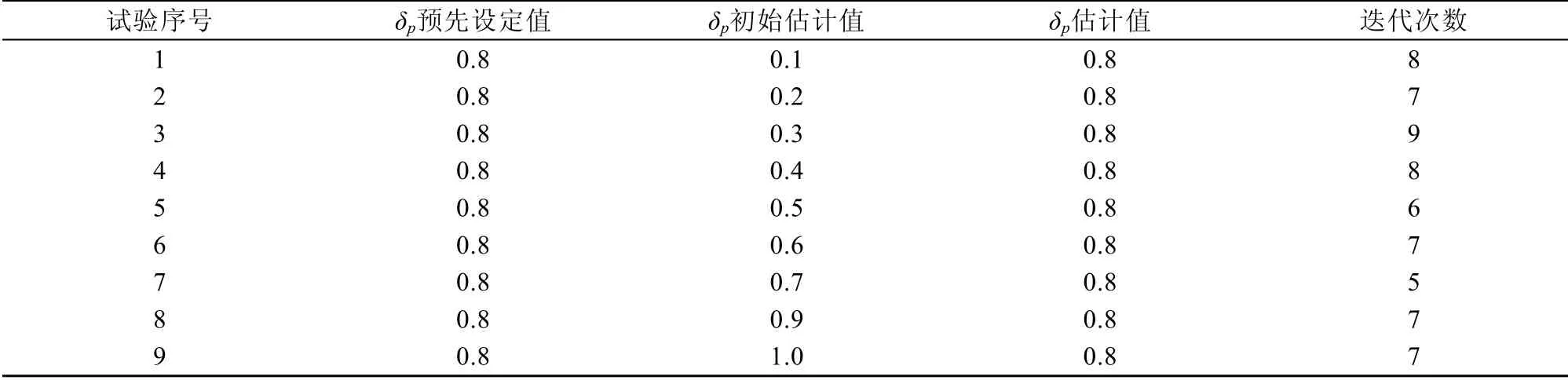
表1 不同初始估計值下海冰模式融池方案的參數估計結果Table 1.Results of melt pond parameter estimation under different first-guess values

3 北極多年冰、一年冰融池縱橫比參數估計

大量融池觀測數據統計表明[20,42], 融池覆蓋率與融池所在海冰類型有關, 多年冰表面較為粗糙, 受到冰脊等地形限制, 傾向于形成覆蓋面積小、深度大的融池。而一年冰表面平整, 易于形成覆蓋面積大、深度淺的融池。因此, 多年冰上融池覆蓋率較低, 一年冰上融池覆蓋率高。本文所優化的參數為融池縱橫比參數, 它是融池深度和融池覆蓋率的比值, 與海冰類型具有密切關系。為此, 在驗證了參數估計算法的可靠性之后,利用MODIS觀測數據, 分別對北極多年冰海域和一年冰海域, 選擇代表性位置, 進行參數估計。

3.1 研究位置選取

多年冰為歷經至少一個夏天仍然存在的海冰。據此, 本研究中利用海冰密集度資料HadISST1, 確定多年冰范圍為在3—9月一直被海冰覆蓋的海域, 一年冰范圍則為3月被海冰覆蓋、9月無海冰覆蓋的海域。圖 5為2005年的3月和9月月平均海冰密集度的二維分布, 從圖中可以看出9月邊緣海的海冰損失最為嚴重, 俄羅斯以北的近海海域幾乎已無海冰存在。因此, 本文選擇的多年冰研究位置位于加拿大北極群島以北的120°W、80°N, 在圖5b中為白色實心正方形所在位置, 一年冰研究位置位于喀拉海的90°E、78°N, 在圖5b中為白色空心正方形所在位置。

圖5 2005年3月(a)和9月(b)的北極海冰密集度.(b)中白色實心及空心正方形分別為融池縱橫比參數估計的多年冰區域(120°W, 80°N)及一年冰區域(90°E, 78°N)Fig.5.Sea ice concentration of March 2005 (a) and September 2005 (b).The white filled square in (b) is the multi-year ice region (120°W, 80°N) and the white hollow square is the first-year ice region (90°E, 78°N) for melt pond aspect ratio parameter estimation

3.2 融池參數估計試驗設計

本文主要研究伴隨模式在海冰融池參數估計中的應用, 為此設計了以下兩組試驗。(1)多年冰參數估計試驗。使用多年冰位置處2005年的MODIS觀測數據約束模式, 先將MODIS數據插值到1 h, 然后將目標函數定義為逐小時的模擬與觀測誤差平方和。融池縱橫比參數的初始估計值設定為0.7。考慮到在融池的發育演化過程中融池覆蓋率和融池深度的變化不完全同步[7], 對于融池發展的不同階段, 模式中應該使用不同的參數。為此, 根據MODIS融池覆蓋率資料特點, 將插值后的MODIS數據從5月9日—9月6日, 每隔8天分為一段, 共分為15個時間段, 每個時間段估計一個參數。以多年冰位置處的JRA55-do數據作為強迫場驅動ICEPACK對單點海冰狀態進行模擬, 模擬時間為2005年1月1日—5月9日, 積分步長為3600 s, 初始海冰密集度為100%,初始海冰平均厚度為2.79 m, 初始融池覆蓋率和深度分別為0%和0 m, 熱力學方案選擇糊狀層方案[43], 短波輻射方案選擇Delta-Eddington方案[44],融池參數化方案選擇CESM方案, 使用的ITD有5個厚度類別(見表2), 冰層垂向上分為等間距的7層, 雪層為1層, 其他為模式的默認設置。從5月9日開始分段積分, 每個時間段內, 參數估計的流程與2.3中相似, 并直接使用了MODIS觀測數據, ICEPACK正向積分8天, 融池伴隨模式反向積分8天, 將該段積分得到的海冰-融池狀態作為下一時間段正向積分的初始條件。分段積分完成后, ICEPACK接著從2005年9月6日積分到2006年1月1日。(2)一年冰參數估計試驗。一年冰試驗使用一年冰位置處2005年的MODIS觀測數據約束模式, 使用一年冰位置處2005年的JRA55-do數據作為大氣強迫, 而初始海冰平均厚度則設定為1.80 m。其余設置與多年冰試驗相同。

表2 本文所使用海冰厚度類別Table 2.Ice thickness distribution used in our experiment

3.3 多年冰上融池縱橫比參數的估計

多年冰參數估計試驗結果如圖6所示。從圖中可以看出, 該點觀測的融池覆蓋率存在兩個相鄰峰值。自5月9日開始, 融池覆蓋率逐漸增大,到6月26日, 開始快速增長, 7月20日達到第一個峰值, 約為30%。隨后開始下降, 但是在8月初很快又上升到第二個峰值, 約為35%, 之后開始持續的下降過程。使用默認參數0.8的模擬與MODIS觀測相差較大, 模擬的融池覆蓋率偏小。尤其是在6月底至7月20日之間, 觀測值大于20%, 然而模擬的融池覆蓋率接近于零, 未能模擬出觀測中融池覆蓋率的上升, 模擬與8天一次的MODIS觀測的均方根誤差為16.69 %。使用估計參數模擬時, 對于每一個分段, 融池縱橫比參數使用該段的估計值, 初始條件使用上一段的積分終值。使用估計的參數值后, 模擬的融池覆蓋率增大, 與MODIS觀測更為接近, 均方根誤差為7.19%, 與使用默認參數值的結果相比減小了56.93%。由此可見, 使用估計的融池參數, 可以有效地降低融池覆蓋率的模擬誤差。但是, 并非每個時間段的模擬結果都能得到優化, 比如8月13日之后的時間。這可能是由于這個時間段其他參數對融池的影響更大。比如, 過低的氣溫導致融水過早減少, 此時僅僅調整融池縱橫比這一個參數是不夠的。

圖6 多年冰區域使用估計的融池參數模擬的融池覆蓋率(紅色線), 使用默認參數模擬的融池覆蓋率(藍色線)以及樣條插值后的MODIS觀測(黑色線, 方塊標注的是MODIS原始觀測)之間的對比Fig.6.Comparison between simulated melt pond fraction using estimated pond parameter (red), simulated melt pond fraction using the default parameter (blue) and the MODIS observation (black, The MODIS pond fraction observation is interpolated using spline interpolation, and the squares mark the original MODIS observations) in MYI region.

多年冰參數估計值有明顯的時間變化。融冰期初期, 5月9日—6月2日, 參數值較大, 達到3左右。6月2日—6月26日, 參數值下降到大約1左右。6月26日—8月29日, 參數值進一步下降到0.05以下。融冰期末尾, 8月29日—9月6日的時間段內, 參數值又上升到0.8的默認值。整體來看, 多年冰上估計的融池參數從融冰初期至融冰末期呈下降趨勢。這與使用默認參數值模擬的融池覆蓋率與觀測的差異有關, 參數估計算法不斷調整參數值以使得模擬和觀測的誤差減小。在5月和6月, 使用默認參數值模擬的融池覆蓋率略高于觀測值, 因而估計的縱橫比參數值大于默認值。這是因為融池縱橫比增大, 按照公式( 1 )將增加融池深度, 在融水體積不變的情況下, 在進一步積分中將減少融池面積, 起到修正融池覆蓋率模擬的效果。在7月和8月, 使用默認參數值模擬的融池覆蓋率遠低于觀測值, 估計的參數值很小。這是因為融池縱橫比減小, 按照公式( 1 )將減少融池深度, 在融水體積不變的情況下, 在進一步積分中將增加融池面積, 起到修正融池覆蓋率模擬的效果。當然這樣的過程只能在其他因子不變的情況下發生。

3.4 一年冰上融池縱橫比參數的估計

一年冰參數估計試驗結果如圖7所示。從圖中可以看出, 該點的MODIS融池覆蓋率序列存在一個峰值, 在6月上旬增加到15%左右, 隨后下降為零。使用默認參數的模擬與MODIS觀測相差較大, 模擬的融池覆蓋率偏大, 在觀測融池覆蓋率降低為零后, 模擬融池覆蓋率仍然為15%以上, 持續時間過長, 直到9月初仍有融池存在,模擬與觀測的均方根誤差為6.31%。使用估計的參數值后, 模擬的融池覆蓋率明顯下降, 與MODIS觀測吻合得更好, 均方根誤差為4.60%,減小了27.10%。由此可見, 使用估計的融池參數,可以有效地降低融池覆蓋率的模擬誤差。注意到6月18日之后, 觀測融池覆蓋率降低為零, 模擬的融池覆蓋率未能抓住這種特征。這可能是由于實際中一年冰完全融化, 而模式中海冰仍然存在。使用估計的融池參數, 也不能完全消除這種誤差。

圖7 一年冰區域使用估計的融池參數模擬的融池覆蓋率(紅色線), 使用默認參數模擬的融池覆蓋率(藍色線)以及樣條插值后的MODIS觀測(黑色線, 方塊標注的是MODIS原始觀測)之間的對比Fig.7.Comparison between simulated melt pond fraction using estimated pond parameter (red), simulated melt pond fraction using the default parameter (blue) and the MODIS observation (black, The MODIS pond fraction observation is interpolated using spline interpolation, and the squares mark the original MODIS observations) in FYI region.

一年冰上估計的參數值較大, 達到10以上,和默認參數值0.8存在較大的差異。一年冰上使用默認參數值模擬的融池覆蓋率高于觀測值, 因而估計的參數值較大。對于海洋生態模式, 已有研究[45]指出, 相比固定參數以及僅隨空間或時間變化的參數, 使用伴隨同化方法得到的隨空間和時間變化的生態參數更為優越, 符合生態機制。對于本文研究的融池參數, 由于融池過程在時間及空間上的明顯變化, 隨時間和空間變化的參數可能更為合理。

4 結論與討論

海冰模式中的融池參數化方案存在某些經驗性的參數, 使用伴隨模式方法可以對這些參數進行估計以減小不確定性。本文針對CICE6.0海冰模式中的CESM融池參數化方案進行了參數估計。首先, 根據伴隨模式代碼生成的規則構建了融池方案的伴隨模式。接著, 給出了使用伴隨模式估計融池參數的算法流程。這一算法包括融池方案、融池方案的伴隨模式及L-BFGS極小化算法。利用控制試驗數據作為觀測約束, 進行了該參數估計算法的驗證。最后, 利用MODIS觀測資料作為約束條件, 對CESM方案的參數進行了分時間段、分區域的估計。主要結論如下。

1.本文所采用的代碼直接轉換方法可以正確地得到融池參數化方案的切線性模式和伴隨模式。構造的伴隨模式可以正確地計算目標函數的梯度。使用正向模式、伴隨模式和極小化算法組成的參數估計算法可以用于對CICE6.0的CESM融池參數化方案中的參數進行估計。

2.使用伴隨模式方法得到的參數估計值是隨時間和空間變化的, 區別于CICE6.0中的默認固定參數值。在北極夏季不同時間段, 多年冰海域和一年冰海域的融池參數估計值具有較大差異。這與融池過程的時空變化有著密切關系。

3.使用得到的最優參數估計值進行模擬, 對選取樣本區域融池的模擬誤差減小。在兩個單點的模擬中, 相比使用默認參數值的試驗, 多年冰上模擬融池覆蓋率和MODIS觀測數據的均方根誤差減小了56.93%, 一年冰上均方根誤差減小了27.10%。

融池的時空變化受到輻射、氣溫、降水、海冰類型等多種變量的影響, 具有復雜的機制。本文主要以融池縱橫比參數作為估計和優化的目標,研發了融池伴隨模式。一年冰上估計的參數大于多年冰上估計的參數。這一點不同于融池在一年冰上更淺的特征。這可能是由于融池伴隨模式只考慮了一個參數融池縱橫比, 并且在一年冰及多年冰區域都只選擇了一個點進行參數估計試驗,為了修正一年冰上模擬融池覆蓋率偏大的特征,必須增大融池縱橫比參數, 以增加融池深度, 進而減小融池覆蓋率。這在數學上是合理的, 在物理上卻不一定反映了這一點的真實情況。但本研究的目標是以融池為例探討伴隨模式在海冰模式參數估計中的應用, 本文研究結果表明伴隨模式方法可以應用于海冰融池參數的估計, 并得到了優化的融池縱橫比參數, 為進一步使用伴隨模式估計融池參數化方案中的其他參數, 從整體上優化融池和海冰模式的模擬提供了基礎。

融池縱橫比決定了融水在融池面積和融池深度兩者之間的分配, 但只是CESM方案中重要參數之一, 方案中的融水流失比參數則可以直接影響融池體積。由于各物理過程之間的復雜相互作用, 下一步應改進伴隨模式, 比如發展二維的海冰伴隨模式, 對多個重要參數同時進行估計和調整以達到融池模擬最優的目的。此外, CESM方案的物理過程比較簡單, 針對物理過程更完備的方案研發其伴隨模式, 并進行參數估計, 將會改善海冰模式中融池過程的描述, 提高海冰模式的準確性。