對數預不變凸模糊映射及其應用

白玉娟

（隴東學院 數學與統計學院，甘肅 慶陽 745000）

眾所周知，凸性理論在對策論、工程、管理科學和最優化理論中起著非常重要的作用。然而，許多實際問題形成的數學模型，常常不能滿足凸規劃的基本要求，于是出現了對各種各樣的廣義凸性以及與數學規劃問題相關聯的一些基本性質的研究。1981 年，Hanson 提出了不變凸函數的定義并將其推廣為擬不變凸和偽不變凸[1]。1988 年，Weir T 和Mond B 提出預不變凸函數的定義，并研究了此類函數在最優化中的應用[2]。2001 年，楊新民給出了預不變凸函數的其他性質[3]，隨后顏麗佳提出了強預不變凸函數[4]。具體的優化問題數學建模過程中，往往還需要模糊數描述不確定參數，因此，關于模糊凸分析理論與其相對應的模糊優化問題的研究，引起了廣大學者的興趣。1994 年，NOOR M A 給出了預不變凸模糊映射和模糊不變凸集的概念[5]。1999 年，SYAU Y R 定義了η為向量值函數的預不變凸性，得到預不變凸模糊映射的兩個刻劃定理，并討論了其在優化理論中的應用[6]。1992 年，Nanda S 提出了對數凸模糊映射[7]。2006 年，張成利用模糊數的表示定理，證明了對數凸模糊映射一些基本性質[8-9]。本文提出對數預不變凸模糊函數的概念，討論對數預不變凸模糊函數的若干性質及此類函數在模糊數學優化問題中的應用。

1 預備知識

定義1[10]56記E=且滿足：

（1）u是上半連續的；

（2）u是正規的，即存在x0∈R，使得u(x0)=1；

（3）u是凸模糊集，即對 ?x,y∈R，α∈[0,1]，有u(αx+(1-α)y) ≥min{u(x),u(y)}；

（4）[u]0=cl{x∈R:u(x)＞ 0}是緊集。

任意的u∈E，u被稱為模糊數且E稱為模糊數空間。顯然，任意的u∈E，α∈[0,1]，

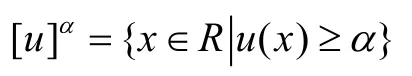
是非空有界閉集。

定理1[10]58設u∈E，則u-(α)與u+(α)是[0,1]上的函數且滿足：

（1）u-(α)單調非降左連續；

（2）u+(α)單調非增左連續；

（3）u-(α)，u+(α)在處是右連續的；

（4）u-(α)≤u+(α)。

反之，對任何滿足上述條件(1)-(4)的函數u-(α)，u+(α)，存在唯一的u∈E，使得

定義2設u,v∈E，對于任意的α∈[0,1]，如果

即u-(α)≥v-(α)且u+(α)≤v+(α)，則稱。稱u=v當且僅當且

對u∈E，當且僅當

稱u為零模糊數，記作

定義3設集合I(?R)，如果存在一個向量函數η:R n×Rn→Rn，使得對 ?t,t'∈I,?λ∈[0,1]滿足t'+λη(t,t')∈I，則集合稱I(?R)是不變凸集。

定義4設I(?R) 為一個不變凸集，一個模糊映射f:I→E稱為預不變凸模糊映射當且僅當：對?t,t'∈I,?λ∈[0,1]，有

2 對數預不變凸模糊映射及其應用

定理2[11]設{a(α),b(α)}(0≤α≤ 1)是R上的一族非空有界閉區間且滿足：

（1）[a(α2),b(α2)] ?[a(α1),b(α1)]，對所有的0＜α1≤α2；

（2）對任何非減列{αk} ?[0,1],α k↑α，有

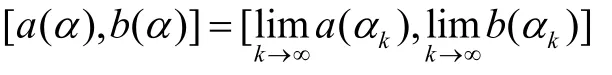
則[a(α),b(α)]為某一模糊數A的截集；反之，若[a(α),b(α)]為某一模糊數A的截集，則必須滿足條件（1）和（2）。

由0＜A-(α)≤A+(α)，得

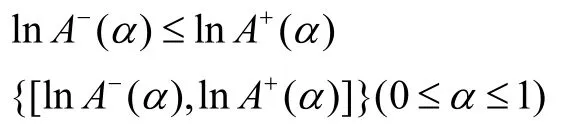
為R上的一族非空有界閉區間。

因為當(0≤α1≤α2)時，

所以

如果對于任何非負遞減

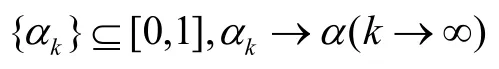
有

根據對數函數的連續性，得

于是由定理2 可知，

表示一個對數模糊數。

定理3設A,B∈E+，若A≥B，則有

（1）lnA≥lnB；

（2）Aα≥Bα(α＞ 0)。

定義5 設I?R為不變凸集，f:I→E+為定義在I上的模糊映射。

（1）若對 ?t,t'∈I,?λ∈[0,1]，有

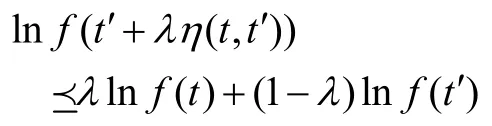
則稱f是對數預不變凸的。

（2）若對 ?t,t'∈I,t≠t',?λ∈[0,1]，有

則稱f是嚴格對數預不變凸的。

定理4設I?R為不變凸集，f:I→E為模糊映射，則f為I上的預不變凸函數的充要條件為：對任給的α∈[0,1]，f-(x,α),f+(x,α)均為I上的預不變凸函數。

定理 5設I?R為不變凸集，若模糊映射f:I→E+為對數預不變凸的，則模糊映射f為預不變凸的。

證明因為

所以 -lnx為凸函數，從而對a＞0,b＞ 0，(a,b∈R)，λ∈[0,1]，有

即

設

為I上的對數預不變凸模糊映射，則對任意的x,y∈I及任意的λ∈[0,1]，有

根據模糊數對數定義，對任意α∈[0,1]，有

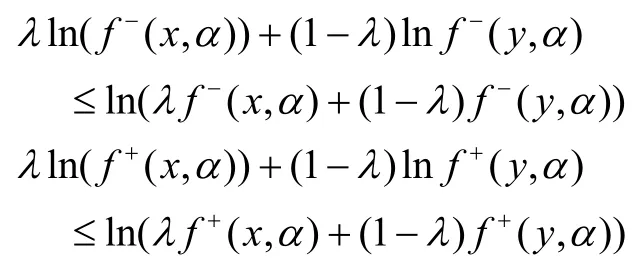
從而，有

這說明，對任意的α∈[0,1]，f-(x,α),f+(x,α)均為預不變凸函數，f為預不變凸模糊映射。

3 對數預不變凸模糊數值函數與優化問題

對于求模糊數值函數f:I→E+的非約束模糊優化問題記為：

Minimizef(t)，Subject to t∈I。

定義6設I?R關于η:R×R→R是不變凸集，f:I→E+為I上的模糊數值函數，t0∈I，

（1）若存在t0的某個鄰域N(t0)，當t∈I∩N(t0)有則稱t0為f的局部最優解。

（2）若對?t∈I有則稱t0為f的全局最優解。

定理 6設I?R為不變凸集，若模糊映射f:I→E+為對數預不變凸的，則f的局部最優解必為全局最優解。

證明設x0為f在I上的局部最小值點。若x0不是全局最小值點，則存在y0使得f(y0)＜f(x0)，由于模糊映射f為對數預不變凸的，即對任意的λ∈[0,1]，有

定理7設I?R為非空不變凸集，若模糊映射f為對數預不變凸的，Ω 為f的全局最優解的集合，則Ω 也是關于η的不變凸集。

證明?x,y∈Ω，由于Ω 為f的全局最優解的集合，于是

又模糊映射f為對數預不變凸的，即對任意的λ∈[0,1]有，

又因為x是全局最優解，所以

故Ω 是關于η的不變凸集。

定理8設I?R為非空不變凸集，若模糊映射f為嚴格對數預不變凸的，則f在I上的全局最小值點是唯一的。

證明設x0為全局最小值點，y0也為最小值點且x0≠y0，則

因為模糊映射f為嚴格對數預不變凸的，即對任意的λ∈[0,1]，有

這與x0是f在I上的全局最小值點矛盾，故f在I上的全局最小值點是唯一的。

定理9設I?R為非空不變凸集，若模糊映射f為對數預不變凸的，則水平集合

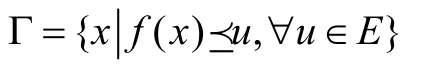
為不變凸集。

證明?x,y∈Γ，都有，即

因為模糊映射f為對數預不變凸的，即對任意的λ∈[0,1]有，

故Γ為不變凸集。