基于高速均勻性數據分析的輪胎固有頻率測算方法

李慧敏，劉寶濤，張凱凱，王龍慶

（青島森麒麟輪胎股份有限公司，山東 青島 266229）

輪胎是由多種材料經多道工序復合而成的產品，其生產過程不可避免地會存在質量、剛性和尺寸的不均勻性，這種不均勻性在輪胎高速運轉過程中會產生徑向力、側向力及縱向力波動，波動幅度達到一定程度會影響汽車的振動和噪聲狀況[1-3]。輪胎高速均勻性試驗機是一種專用于測試輪胎在高速和負荷情況下力學特性參數的檢測設備，不同于低速均勻性檢測，它可以更準確地模擬輪胎在高速運轉過程中的力學特性，因此其檢測數據更具參考性。

高速均勻性檢測的是輪胎高速運轉過程中徑向力、縱向力和側向力的周期性變化，是時域上復雜的周期性力的波動，通常采用傅里葉級數的方法將其分解成多個諧波的疊加。每次諧波的頻率對應的是相應的輪胎滾動頻率的倍數。當某一速度下的某一諧波頻率接近輪胎的固有頻率時，會引起胎體的共振，力的響應將發生“爆炸性”的增長。因此通過對力的強迫響應的觀測，可以計算輪胎的固有頻率。

本工作基于高速均勻性數據，通過對徑向力的分析，測算徑向一階固有頻率。

1 測算方法

使用ZF HSU-L-5.3型高速均勻性試驗機（德國采埃孚集團產品）按照GMW 15120（2012）獲得205/50ZR17輪胎一組高速均勻性試驗數據，試驗機數據處理系統自動進行傅里葉變換，輸出各次諧波的幅值，見表1。

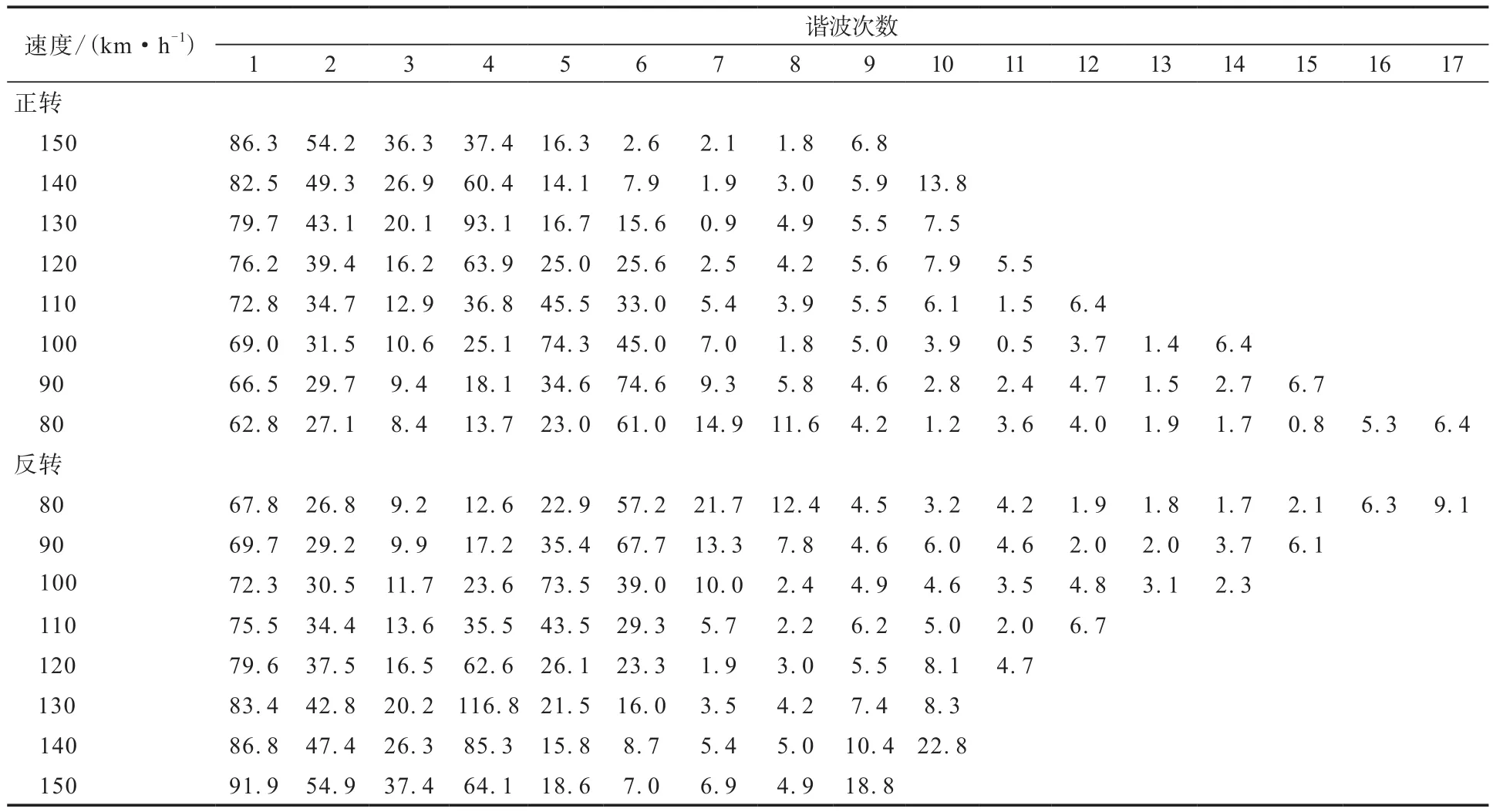
表1 205/50ZR17輪胎高速均勻性徑向力各次諧波幅值 N

由表1可見，徑向力各次諧波幅值整體隨諧波次數增大而減小，一次諧波幅值較大，其余數據較為雜亂，不易進行分析。

使用Minitab軟件對不同速度下各次諧波的幅值進行分析，查看諧波幅值與輪胎速度的相關性，徑向力1—6次諧波幅值與速度的二次擬合曲線如圖1—6所示。徑向力1—6次諧波幅值與速度的二次擬合曲線方程分別如下：

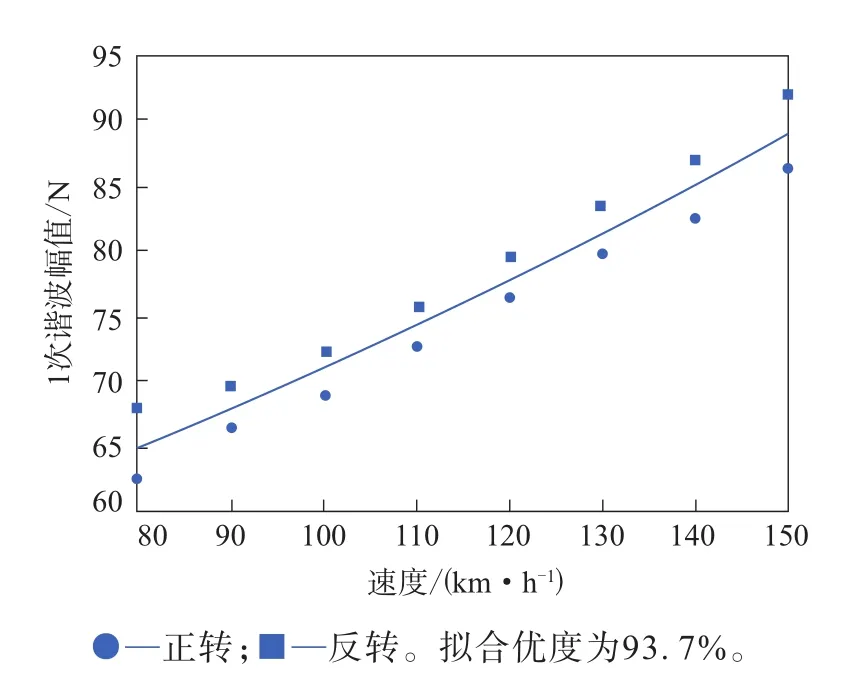
圖1 徑向力1次諧波幅值與速度的二次擬合曲線

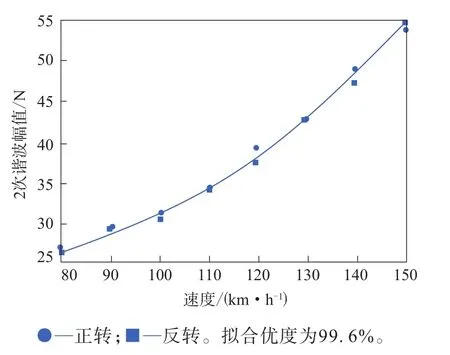
圖2 徑向力2次諧波幅值與速度的二次擬合曲線

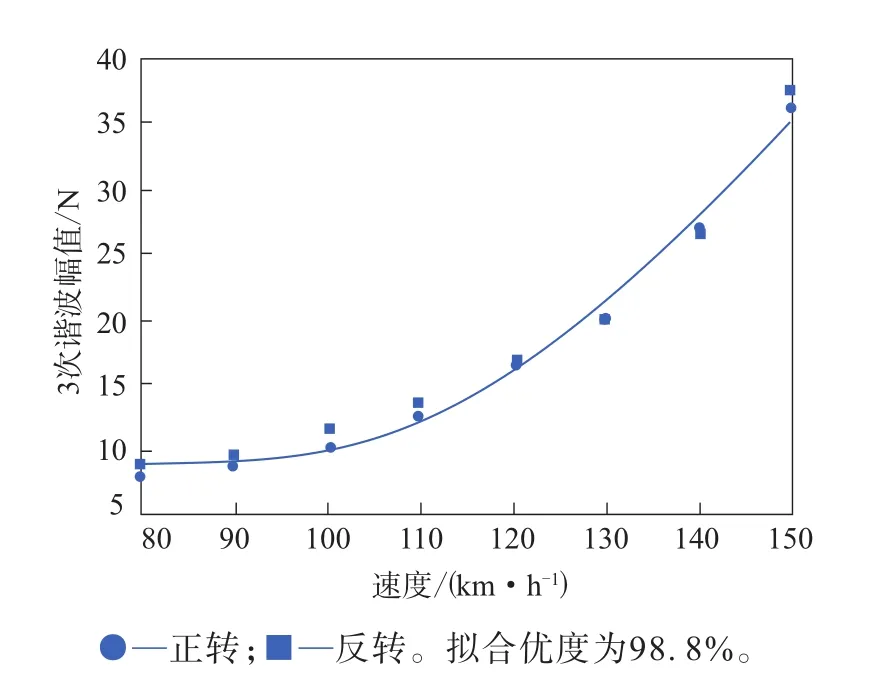
圖3 徑向力3次諧波幅值與速度的二次擬合曲線

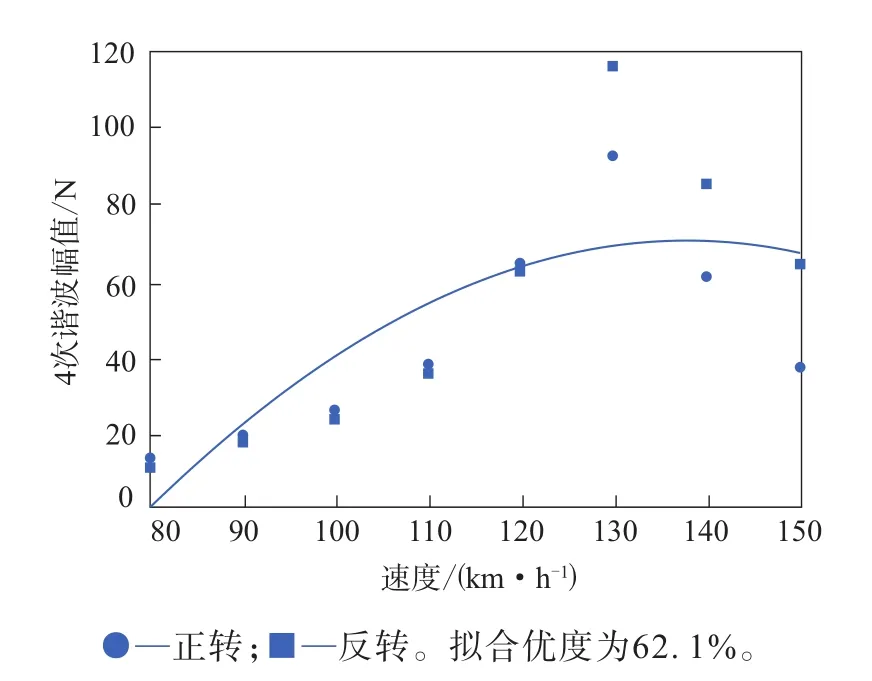
圖4 徑向力4次諧波幅值與速度的二次擬合曲線

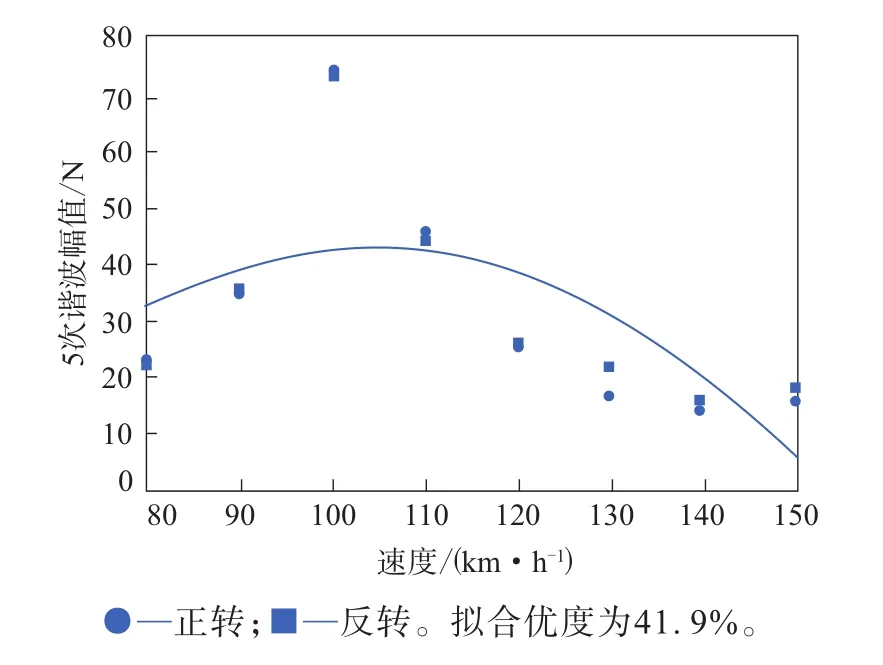
圖5 徑向力5次諧波幅值與速度的二次擬合曲線

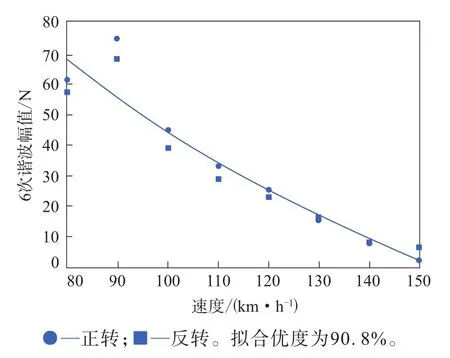
圖6 徑向力6次諧波幅值與速度的二次擬合曲線

由圖1—6可以看出：徑向力的前3次諧波幅值與速度的二次擬合曲線的擬合優度均在90%以上，呈現出很強的速度依賴性；徑向力的4—6次諧波幅值大部分仍落在與速度的擬合曲線上，但有個別速度對應的諧波幅值出現了突變，且隨著諧波次數的增大，出現突變的數據對應的速度減小。

對以上數據突變的諧波幅值進行頻率（f）計算：

式中，r為輪胎轉速，n為諧波次數，v為輪胎速度，l為輪胎滾動周長。

計算得各諧波幅值突變數據對應的頻率見表2。

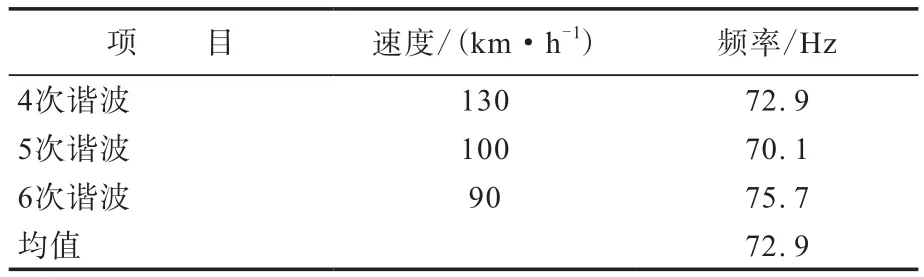
表2 諧波幅值突變數據對應的頻率計算結果

由表2可以看出，諧波幅值突變數據對應的頻率趨于一致，均值為72.9 Hz，即徑向力的4次、5次、6次諧波分別在130，100，90 km·h-1速度下的頻率處激起共振，導致力傳感器感應到的力大幅增大，由于輪胎的徑向一階固有頻率一般分布在60～100 Hz內，頻率越低，能量越高，越容易被激起振動，因此測算得到的頻率均值為輪胎徑向一階固有頻率，同時可以粗略地認為，被激起的平均幅值為輪胎一階徑向模態的力的響應幅值。

2 正確性驗證

2.1 理論驗證

對于無阻尼自由系統，其固有頻率（f0）計算公式如下：

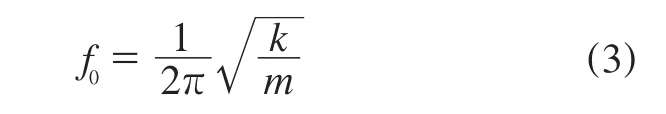
式中，k為徑向剛度，N·m-1；m為質量，kg。

由式（3）可以看出：不考慮阻尼，結構的固有頻率只受徑向剛度和質量的影響，質量增大，結構的固有頻率減小；徑向剛度增大，結構的固有頻率增大。

不同于無阻尼自由系統，輪胎具有復雜的結構和多個自由度，并有阻尼，但結構的固有頻率的主要影響因素仍是徑向剛度和質量，且作用方向一致，阻尼對固有頻率的影響非常有限[4-5]。

選取某配套項目試制的6個方案試驗輪胎及標準輪胎分別進行高速均勻性試驗，按上述方法獲取輪胎徑向一階固有頻率及徑向力幅值，結果見表3。

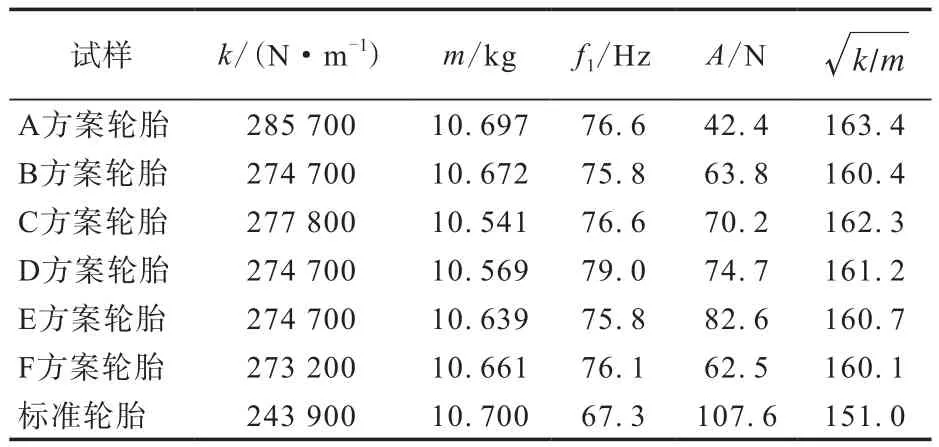
表3 試制方案及標準輪胎的徑向一階固有頻率計算值

對f1與的回歸擬合可以得到如下方程：

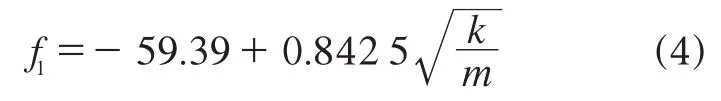
調整后的擬合優度高達84.3%，因此認為此數據模型有效，即質量增大，結構的固有頻率減小；徑向剛度增大，結構的固有頻率增大，與理論相符。

對A與k回歸擬合可得如下方程：

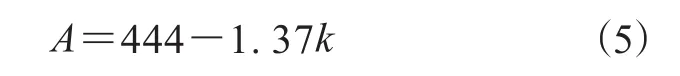
調整后的擬合優度為75.7%，因此認為模型有效，徑向剛度增大，低頻段輸出力的幅值減小，與理論相符。

2.2 力傳感函數試驗驗證

對方案A和E輪胎同時進行力傳感函數試驗，獲取徑向一階固有頻率。根據GMW 14876（2014）法規進行參數設定，試驗采用SCADAS SCM2E05（32 CHs）（日本西門子公司產品）數據采集設備，Test Lab 18A型分析系統，PCB Hammer 086C03型激勵傳感器，PCB Tri-axis 356A32型加速度傳感器。

力傳感函數試驗結果如圖7所示，兩種方法測算的徑向一階固有頻率對比見表4。

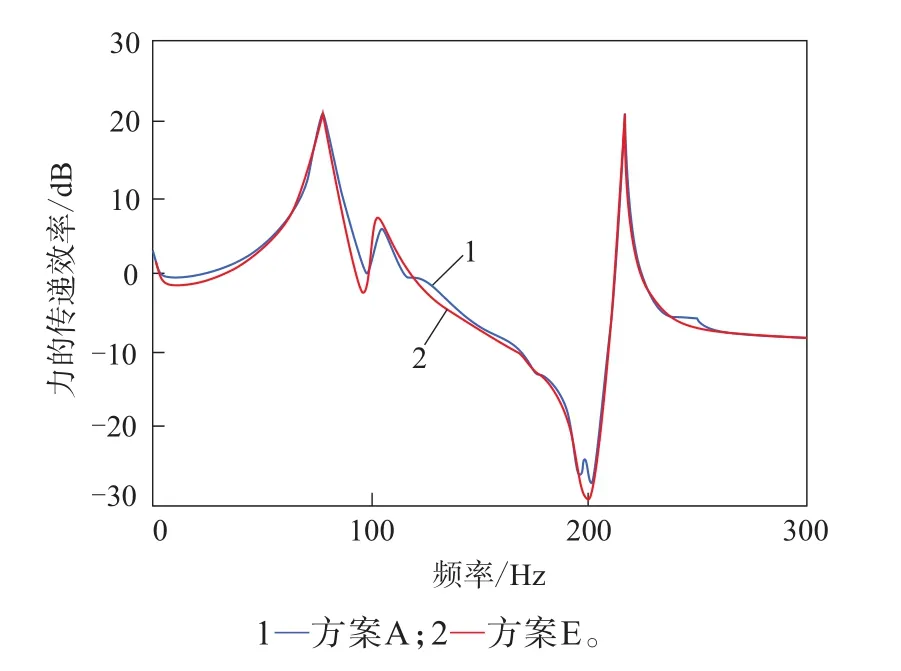
圖7 力傳感函數試驗結果

表4 兩種方法測算的徑向一階固有頻率對比 Hz

由圖7和表4可見，通過兩種方法獲取的徑向一階固有頻率基本一致，相差約1 Hz，這可能是因為力傳感函數測量的是靜態輪胎的徑向一階固有頻率，而通過高速均勻性數據測算的是工作狀態下的徑向一階固有頻率，由于輪胎生熱，胎體簾線模量減小，輪胎整體剛度減小，導致固有頻率減小。

通過固有頻率影響因素和力傳感函數測算的驗證，確認通過高速均勻性數據測算f1的方法是可行的。可以通過減小高速均勻性試驗的速度梯度來提升測算的精確度，無特殊要求時高速均勻性試驗一般采用10 km·h-1的速度梯度，若用于測算徑向一階固有頻率，可以針對某一較小的速度段將速度梯度調整為2 km·h-1。

3 結構設計對固有頻率的影響

對215/50R17輪胎不同結構設計方案（見表5）進行分析。

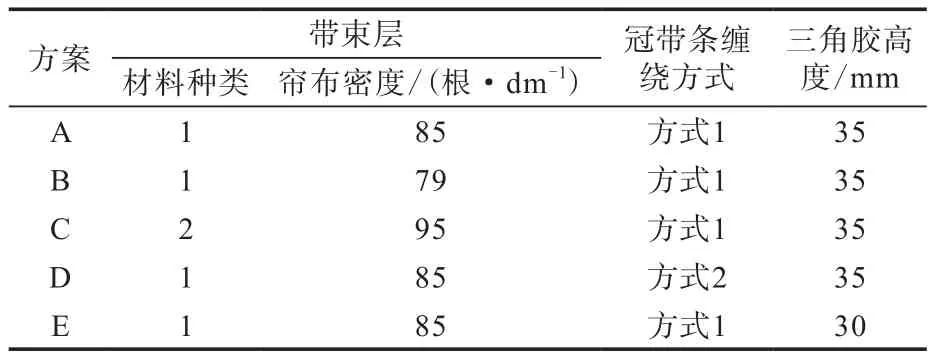
表5 結構設計方案

結合表3和表5可以看出以下幾點。

（1）對比方案A與B，帶束層簾布密度減小，輪胎的徑向剛度降低，質量減小，徑向一階固有頻率降低，因此調整帶束層簾布密度，徑向剛度對固有頻率的影響大于質量。

（2）對比方案A與C，帶束層簾線種類和簾布密度均發生變化，徑向剛度和質量均減小，徑向一階固有頻率不變，說明帶束層設計的變化對固有頻率的影響不大。

（3）對比方案A與D，冠帶條纏繞方式調整，徑向剛度降低，質量減小，徑向一階固有頻率增大，因此調整冠帶條纏繞方式，質量對固有頻率的影響大于徑向剛度。

（4）對比方案A與E，三角膠高度減小5 mm，徑向剛度降低，質量減小，徑向一階固有頻率降低，因此調整三角膠高度，徑向剛度對固有頻率的影響大于質量。

4 結論

（1）通過Minitab軟件對高速均勻性數據中各次諧波幅值進行分析，對于發生突變的數據通過其對應的諧波次數和速度計算頻率，多個數據對應的頻率比較接近，其均值可以認為是徑向一階固有頻率，被激起的諧波幅值均值可以認為是共振點的幅值。

（2）可通過減小高速均勻性試驗的速度梯度來提升輪胎固有頻率的測算精確度。

（3）通過高速均勻性測算的固有頻率比通過力傳感函數測得的固有頻率略小，這可能是因為工作狀態下生熱導致輪胎整體剛度減小，固有頻率相應減小。

（4）結構設計對輪胎固有頻率有影響，冠帶條纏繞方式影響較大，帶束層設計對一階徑向固有頻率的影響不大。

本方法測算的是輪胎在一定充氣壓力和負荷下運轉時的固有頻率，更貼合輪胎的實際工作狀態，若合理運用可以在不進行力傳感函數測試的情況下，在測試輪胎高速均勻性數據的同時獲取輪胎的低階固有頻率及幅值，可指導輪胎的結構優化，縮短測試周期，具有很好的實用性。