如何正確運用χ2檢驗——高維表資料齊性檢驗與SAS實現

胡純嚴 ，胡良平 ，2*

（1.軍事科學院研究生院，北京 100850；2.世界中醫藥學會聯合會臨床科研統計學專業委員會，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

對高維表資料進行差異性分析的基本思路是將高維表降為二維表，降維的重要舉措就是按一個因素的全部水平或多個因素的全部水平組合對資料進行分層，從而使每層中的資料都是一個二維表資料。一種特殊的高維表就是分層后的二維表為2×2表（即含一個二值的原因變量和一個二值的結果變量），簡記為“g×2×2表”。此時，就可依據“隊列研究設計（含橫斷面研究設計）”或“病例對照研究設計”，推導出兩套對此種高維表資料進行差異性分析的方法。此法涉及到若干個具體的分析內容，概括地表述為“定性資料的Meta分析［1］”，因篇幅所限，本文只討論g×2×2表資料的齊性檢驗問題。

1 高維表資料齊性檢驗的必要性

1.1 高維表（g×2×2表）資料的表達模式

高維表（g×2×2表）資料的表達模式見表1。

表1 高維表（g×2×2表）的第h層2×2表資料的表達模式

1.2 高維表資料齊性的含義

在高維表資料中，至少有2個因素（或自變量），1個定性的結果變量。除了采用回歸分析可以同時考察多個因素對定性結果變量的影響之外，差異性分析的思路是將其他因素當作分層變量，只研究剩余的一個因素對二值定性結果變量的影響，這被稱為將高維表降維后使其成為二維表。顯然，在分層變量（它可以是1個因素，也可以是多個因素的水平組合）的每個水平下，都有一張二維表。假定分層變量有g（g≥2）個水平，則有g張2×2表（注：本文不考慮g張R×C表）。只有在它們的內部構成基本一致時，才能將它們按某種規則合并或壓縮成一張2×2表。于是，人們將“內部構成基本一致”的g張2×2表資料稱為滿足“齊性的高維表資料”。

1.3 高維表資料齊性檢驗方法概述

如何度量高維表資料是否滿足齊性？若資料取自隊列研究設計，則分層后的各張2×2表的相對危險度（RR）或危險率差（RD）之間接近相等，就可以認定此種高維表資料滿足齊性；若資料取自病例對照研究設計，則分層后的各張2×2表的優勢比（OR，簡稱為優比）之間接近相等，就可以認定此種高維表資料滿足齊性。由于對同一個資料而言，通常OR值與RR值是比較接近的（但必須注意：選擇2×2表資料的第1列還是第2列來計算RR的數值是至關重要的，其中有一個與OR值接近，而另一個與OR值的倒數接近），故在SAS統計軟件［2］中，僅給出基于OR為效應指標的“齊性檢驗”的計算公式和SAS軟件實現方法。然而，在文獻［3-7］中，先給出一個統一的用于齊性檢驗的“Q檢驗統計量”；然后再按照3種效應指標（分別為“相對危險度RR或lnRR”“危險率差RD”和“優勢比OR或lnOR”）分別展開“Q檢驗統計量”。也就是說，實際存在3個不同的用于齊性檢驗的“Q檢驗統計量”。

在SAS/STAT的FREQ 過程［2］中，高維表資料（特指g×2×2表）優勢比齊性檢驗的方法有以下5種 ，其 中 ，“Breslow-Day檢 驗 ”“Breslow-Day-Tarone檢驗”和“Q檢驗”在本質上都是χ2檢驗；“I2度量統計量及其不確定性限值”在本質上是Z檢驗（也可被視為自由度為1的χ2檢驗）；而“Zelen's精確檢驗”在本質上類似于分析二維表資料的Fisher's精確檢驗，即基于超幾何分布而推導出的計算方法。

2 高維表資料齊性檢驗及SAS實現

2.1 高維表資料優勢比齊性檢驗的具體算法

2.1.1 Breslow-Day檢驗統計量與Breslow-Day-Tarone檢驗統計量

Breslow-Day檢驗統計量QBD公式如下，見式（1）：

在式（1）中，QBD為服從自由度為q-1的χ2分布的檢驗統計量。其中，“ORMH”“E(.)”和“Var(.)”分別代表“基于Mantel-Haenszel方法計算的優勢比”“第h層2×2表中第（1，1）網格上的期望頻數”和“第h層2×2表中第（1，1）網格上的方差”，其計算公式分別見下式：

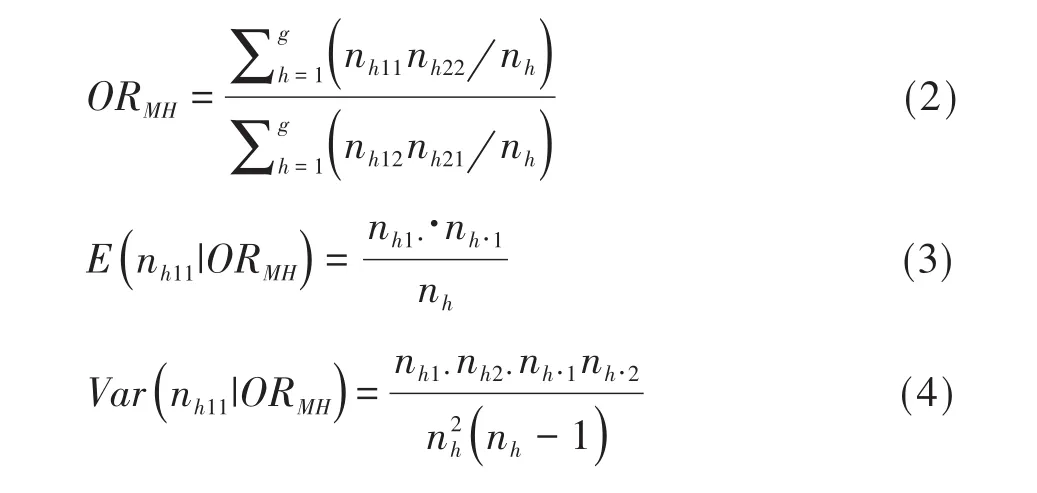
應用式（1）所需要滿足的前提條件：各層2×2表中理論頻數＞5的格子數應大于80.0%。若資料不滿足前述的前提條件，SAS軟件建議改用Tarone's校正的Breslow-Day檢驗統計量，簡稱為Breslow-Day-Tarone檢驗統計量QBDT，見式（5）：

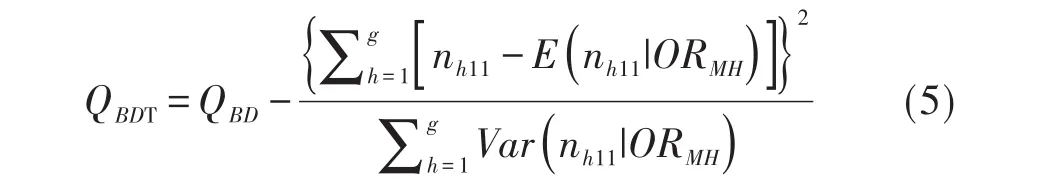
在上式中，QBDT為服從自由度為g-1的χ2分布的檢驗統計量。

2.1.2 Q檢驗統計量

Q檢驗統計量Q的公式如下，見式（6）：

在式（6）中，Q漸近地服從自由度為g-1的χ2分布。分別見下式：

在上述各式的計算過程中，若某一層的表格中有0頻數，就將該層的全部頻數分別加上0.5。

2.1.3 I2度量統計量及其不確定性限值

Higgins和Thompson于2002年提出了I2統計量［2］，它被用于度量在分層2×2表中層間非齊性的一種測度。I2以百分數的形式來表達，它可以被解釋為層間變異占總變異的比例。其計算公式見式（11）：

在式（11）中，“g”代表表的層數，Q的計算公式見前文式（6）。

Higgins和Thompson于2002年提出，通過構建H統計量的置信區間，可以轉換成構建I2的不確定限值（類似于“置信區間”）［2］。首先，定義H統計量如下式：

其次，需要給出log（H）［即ln（H）］的標準誤的計算公式，見式（13）和式（14）：

最后，構建I2的不確定性限值（類似于“置信區間”）。

基于式（16），通過轉換式（15）間接獲得I2的不確定性限值：

當I2為0時，SAS/STAT中FREQ過程將置信限的下限設置為0，并以顯著性水平α取代α/2來決定置信限的上限（注：在本質上，此時所求的就是單側置信區間）。

2.1.4 Zelen's精確檢驗

Zelen's精確檢驗是Breslow-Day近似檢驗的精確版本。用于Zelen's精確檢驗的“參考集”包括所有可能的g×2×2表，它們的行、列和層合計頻數以及各個2×2表中第（1，1）網格上的合計頻數與觀測到的高維表是相同的。在固定邊緣合計的條件下，這個檢驗統計量是觀測到的g×2×2表出現的概率（它可被稱為“理論概率”），它是超幾何分布概率的乘積。

Zelen's精確檢驗的“P值”是前述提及的“理論概率”中小于等于觀測到的“表概率”的“理論概率之和”。這個檢驗與二維表時基于Fisher's精確檢驗［8-10］是相同的。

2.2 高維表資料相對危險度或危險率差齊性檢驗的具體算法

2.2.1 高維表資料相對危險度RR齊性檢驗的具體算法

基于“g×2×2表資料”估計共同相對危險度的前提條件是高維表資料應滿足齊性。針對“相對危險度”的齊性檢驗（也稱為異質性檢驗）的具體方法如下［3-5，11］：

在式（20）中，RRMH為共同相對危險度，其計算公式見式（21）；Q為服從自由度為df=g-1的χ2分布的檢驗統計量。

基于Mantel-Haenszel估計量（簡稱MH估計量）估計高維表資料共同相對危險度［2］，見式（21）：

2.2.2 高維表資料危險率差RD齊性檢驗的具體算法

基于“g×2×2表資料”估計共同危險率差的前提條件是高維表資料應滿足齊性。針對“危險率差”的齊性檢驗（也稱為異質性檢驗）的具體方法如下［3-5，11］：

在式（25）中，共同危險率差RDMH是基于MH法計算的，見下式：

在式（26）中，權重w′h由下式定義：

2.3 高維表資料優勢比齊性檢驗的SAS實現

2.3.1 問題與數據

【例1】文獻［3］提供了如下資料，試分析5項研究的OR值之間是否滿足齊性。見表2。

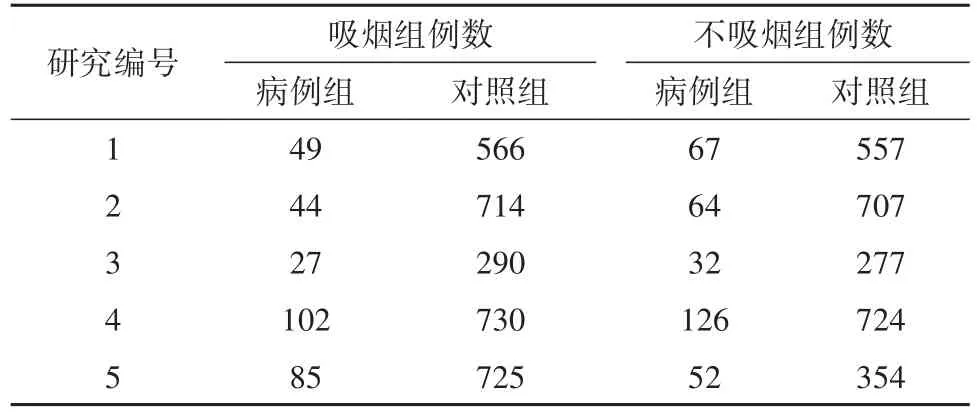
表2 吸煙與肝細胞癌關系的5項病例對照研究結果

【例2】文獻［3］提供了如下資料，試分析6項研究的OR值之間是否滿足齊性。見表3。

表3 鼻咽癌與EB病毒感染關系的6項病例對照研究結果

2.3.2 多項研究的OR值之間齊性檢驗的SAS實現

【例3】沿用例1中的“問題與數據”，試檢驗5項研究的OR值之間是否滿足齊性。

【分析與解答】設所需要的SAS程序如下：

【程序說明】“tables語句”中的選項“cmh”要求對高維表資料進行CMHχ2檢驗；其后括號內的兩個選項的含義分別為：“I2”代表要求計算“I2測度統計量及其不確定性限值”的數值；“QOR”代表要求對各層OR是否滿足齊性進行Q檢驗（注意：系統默認進行“Breslow-Day檢驗”）。“exact語句”中的選項“eqor”，要求對各層OR是否滿足齊性進行Zelen's精確檢驗。

【SAS輸出結果及解釋】

以上是“優比齊性的Breslow-Day檢驗”的輸出結果，QBD=0.6277，df=4，P=0.9599，說明5項研究的OR值之間滿足齊性。

以上是“優比齊性的Q檢驗”的輸出結果，Q=0.6273，df=4，P=0.9600，說明5項研究的OR值之間滿足齊性。

以上輸出的是“優比齊性檢驗I2測度統計量及其不確性限值”的計算結果，I2=0.00%；其不確定性限值的下限與上限都是0.00%。說明5項研究的OR值之間滿足齊性。

【說明】本例實際上沒有進行Zelen's精確檢驗，因為SAS的“日志窗口”中顯示了一條警告信息，告知用戶未進行Zelen's精確檢驗的理由（就本例而言，顯示“頻數太大”）。

【例4】沿用例2中的“問題與數據”，試檢驗6項研究的OR值之間是否滿足齊性。

【分析與解答】設所需要的SAS程序如下：

【程序說明】在SAS程序的“tables語句”的CMH選項后的括號內，加上選項“BDT”，要求輸出Tarone's校正的Breslow-Day檢驗統計量QBDT的數值及其P值。

【SAS輸出結果及解釋】

以上為兩種檢驗的輸出結果：其一，“優比齊性的Tarone's校正的Breslow-Day檢驗”的結果，QBDT=21.9424，df=5，P=0.0005，說明6項研究的OR值之間不滿足齊性；其二，“優比齊性的Zelen's精確檢驗”的結果中，第1行上的“P＜0.0001”是指觀測到的高維表發生的概率，而第2行上的“P=0.0004”是指各種符合特定條件的分層表的概率之和。此值與前面的校正結果“P=0.0005”是比較接近的。

以上為“優比齊性的Q檢驗”的輸出結果，Q=19.2304，df=5，P=0.0017，說明6項研究的OR值之間不滿足齊性。

以上輸出的是“優比齊性檢驗I2測度統計量及其不確性限值”的計算結果，I2=74.00%＞50.00%；其不確定性限值的下限與上限分別是40.69%與88.60%，說明6項研究的OR值之間不滿足齊性。

【說明】因篇幅所限，“高維表資料相對危險度或危險率差齊性檢驗的SAS實現”從略。

3 討論與小結

3.1 討論

本文介紹的統計分析方法主要適用于g×2×2表，而不適用于g×R×C表（R與C中至少有一個大于2）；當分層后的2×2表資料均來自病例對照研究設計時，才適合以“優勢比OR”為效應指標；SAS中的FREQ過程只交待“優勢比OR值的齊性檢驗”，而未提及“相對危險度RR的齊性檢驗”。本文補充介紹了“相對危險度RR”和“危險率差RD”的齊性檢驗方法。本文例3的計算結果（QBD=0.6277，df=4，P=0.9599）與文獻［3］的結果（Q=0.60，df=4，P＞0.05）非常接近；本文例4的計算結果（QBDT=21.9424，df=5，P=0.0005）與文獻［3］的相應結果（Q=12.64，df=5，P＜0.05）相差較大，但最終的結論相同。檢驗統計量Q值上存在的差距，主要原因在于所采取的計算公式不同所致。

【說明】在對g×2×2表資料進行齊性檢驗時，SAS軟件［2］并沒有嚴格區分資料所對應的研究設計類型是隊列研究設計、橫斷面研究設計，還是病例對照研究設計，只是基于不同的數學原理推導出稍有區別的齊性檢驗公式或算法而已，但在輸出結果中，一律顯示“優比齊性檢驗”的字樣；而在統計學教科書（例如：文獻［3-5］）和RevMan軟件［6-7］中，區分得比較清楚。

3.2 小結

本文圍繞g×2×2表資料齊性檢驗問題，解釋了進行齊性檢驗的必要性，介紹了多種齊性檢驗的計算公式，并結合兩個實例，基于SAS軟件給出了優勢比齊性檢驗的結果，對輸出結果給出了解釋，并據此做出了統計結論和專業結論。