植物染色紡紗測配色模型研究

王云鵬 姜 偉 張建明 金凱震 姜 展

（1.青島大學，山東青島，266071；2.德州恒豐紡織有限公司，山東德州，253500）

植物染料是從植物的根、皮、種子、果實、花等部位提取的色素制成的染料，銀杏葉、杏仁殼、指甲花、蘆木等色素提取物都可以應用于紡織品染色［1］。植物染無毒無害、色彩自然，且原料具有可再生性，可應用在棉、麻、羊毛、蠶絲、錦綸等纖維材料上，在國內高端市場具有廣闊的發展前景。然而植物中色素含量低，植物染的成本高；植物染料的染色性能差、上染率低、色牢度低等缺陷也一直限制著植物染的發展［2］。

常用配色模型包括Stearns?Noechel模型、Friele模型、Kubelka?Munk模型、BP神經網絡等。目前應用最為廣泛的是Kubelka?Munk模型，但研究表明Kubelka?Munk模型是基于均勻散射的理論和情況下，并不適用于色紡紗；Stearns?Noechel模型與Friele模型相較具有更為優良的配色表現［3］。在實際生產過程中不單純是三原色的簡單配比，很多時候會出現需要用原有白色纖維進行混和的時候。Friele模型在實際研究的配色中會產生以下幾個問題：一是在矩陣運算中加入白色反射率構成多組分配色極易與原有三原色反射率構成0向量；二是添加了新的反射率數據會使矩陣運算精確程度加大，誤差更加明顯；三是Friele模型是一種基于理論的模型，其運算結果可能會出現負數情況，不符合實際的工業生產［4］。本研究選擇Stearns?Noechel配色模型為研究重點。

1 試驗方案設計與配色模型分析

1.1 問題分析

基于植物染色紡紗的計算機測配色需要考慮眾多實際生產帶來的影響。一是配色模型是否符合工業生產情況和生產模式，需要適合的原料與配比方式。二是植物染上色不均勻導致的局部色差問題會使獲取的反射率數據不穩定，影響測配色的準確性，需要改進測色樣品。三是植物染料的色牢度不高，在工業生產中會產生掉色等情況，大幅增大了擬合配比與實際配比情況的差距，對此需要對配色模型進行一定程度的修正處理。

1.2 Stearns?Noechel模型分析

Stearns?Noechel模型的擬合公式見式（1）和式（2）。

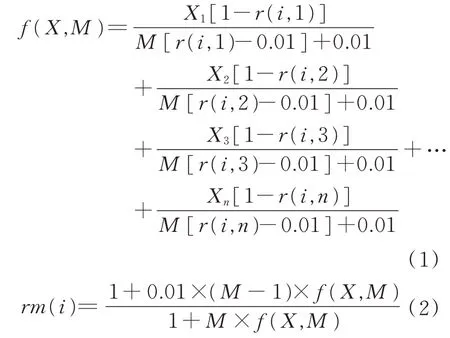
式中：X1、X2、X3、…、X n對應不同組分占總質量的比例，r（i，n）表示不同組分不同波長下的反射率，M為配色公式中與材料相關的未知量，rm（i）為擬合的色紗反射率，f（X，M）為配色公式中的相關代數。

由公式（1）可以看出Stearns?Noechel配色模型實際上是對不同顏色紗線的反射率進行一定比例的擬合，基于人視覺的反射率系數運算后求得在視覺上與標樣最接近的反射率時的配比。Stearns?Noechel模型在運算中的各組分擬合配比是通過不斷循環求出擬合反射率與實際反射率色差最低時的配比，且配比的求得與標樣的顏色種類無關，因此在原公式的基礎上加入白色或其他顏色纖維時不會對后續的配色運算產生影響。通過對模型的分析與實際的配色擬合，發現該模型較適合多種不同顏色組合的配色。

紅、黃、藍、白四組分的Stearns?Noechel模型配色公式見式（3）。

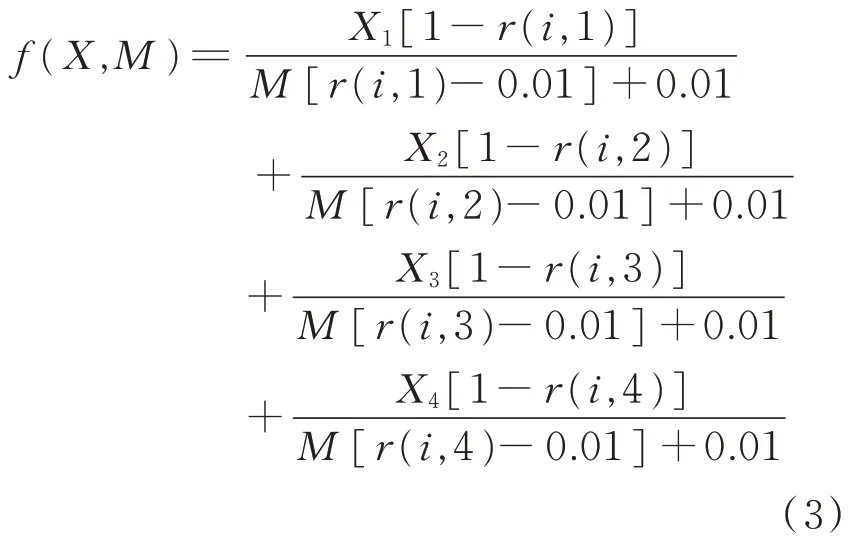
經過針對不同組分的配色模型試驗分析，Stearns?Noechel模型對于紅、黃、藍、白四者相互不同混和有著優異的適應性，分類配色有以下優點。一是針對不同情況，去除生產中不會添加的組分，更加符合實際生產；二是分類配色可以減少不同組分組合之間配色存在的相互影響，提高配色的準確性；三是分類配色同時令不同組分的相互影響因素獨立出來，便于后續的改進。

1.3 試驗樣品制備

選用CM?2300d型分光測色儀，測色方便快捷；原料為茜草、姜黃、靛藍植物染色莫代爾纖維與白色莫代爾纖維，由山東恒豐集團有限公司提供。將不同染色的莫代爾纖維以及不同質量比例的混和纖維經過“開松→混和→梳理→并條→粗紗→細紗”工序后獲得對應的棉網以及細紗，將其中的細紗在一個3 cm×4 cm的黑色板上均勻緊密纏繞3 cm×3 cm面積大小以制成測色樣品。均勻緊密地纏繞在一定程度上減小了測色時產生的色差，緩解了染色不勻導致的反射率數據偏差過大的問題，如圖1所示。最終以不同原料和組合的棉網與細紗樣品作為測色用試樣。

圖1 樣品示意圖

2 試驗結果與改進

2.1 標樣與樣品種類的選擇

以純色原料制成的試樣作為配色中的標樣，不同原料混紡制成的試樣作為樣品。不同類型的標樣與樣品組合對計算機測配色的準確程度具有不同程度的影響。為尋求最佳的測配色標樣與樣品類型，采用纖維網與細紗兩種不同的標樣與樣品相互組合，以此擬合配比得出最合適的樣品類型。樣品中紅、黃、藍、白成分賦予代號R、Y、B、W。不同樣品測配色擬合配比見表1。

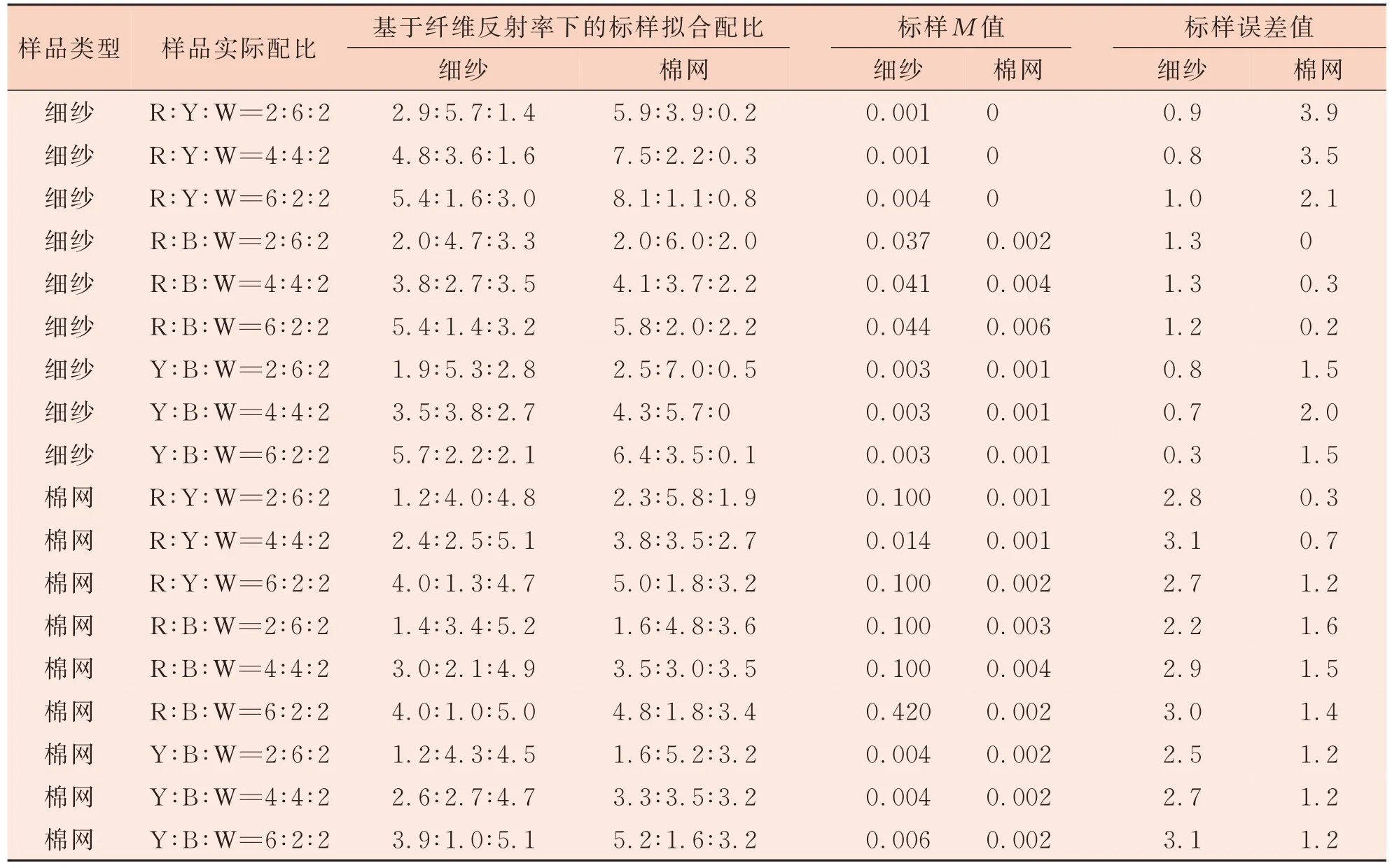
表1 不同樣品反射率測配色擬合配比

在計算機配色過程中，由于擬合機制是計算所能達到的最小色差時的擬合配比，因此當擬合配比與實際配比越為相近時，擬合效果越好，最終生產紗線與樣品的色差會越小。誤差值取擬合配比與實際配比各纖維成分中最大誤差，誤差值的計算見式（4）。

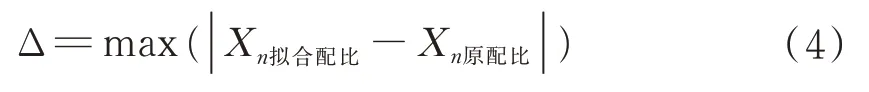
式中：Δ為擬合配比與原配比的誤差值，X n擬合配比為各組分的擬合配比值，X n原配比為各組分的原配比值。

由表1可以看出，棉網與細紗相互之間配色結果與實際配比的誤差值過大，普遍在2到3之間，擬合結果都不理想；棉網標樣與棉網樣品以及細紗標樣與細紗樣品的配色與實際配比的誤差值均在1.0左右，較為符合實際配比情況；其中細紗標樣與樣品的誤差值多小于1.0，棉網標樣與樣品的誤差值多大于1.0，可見細紗標樣與樣品的配色效果最為穩定。因此選用細紗標樣的反射率與細紗樣品進行配色可以提高測配色的準確性。

2.2 修正改進

由于染色與生產的不穩定，在試驗過程中出現過部分配比與預期異常的情況，在分析原因的過程中發現不同標樣的反射率中有以下現象：不同波長下，棉網反射率高于紗線的反射率數據，棉網的反射率數據與紗線的反射率數據在一定的比例范圍內，一般在1.2～1.3。

由此可以假設在紡紗過程中的環境因素影響以及不同紗線之間的相互影響偏向于作用在紗線的整體，即在生產過程中產生的掉色與染色纖維之間的相互作用均勻體現在整個色紗上，針對這個推論可以在原有配色公式的基礎上增加修正系數并初步設定修正系數范圍在0.8～1.5之間，以達到擬合修正實際生產因素的效果。同時基于工業生產中不同的生產環境和生產條件，選擇在不同配色模型中處理，也適應加入修正系數達到配色的準確與穩定。

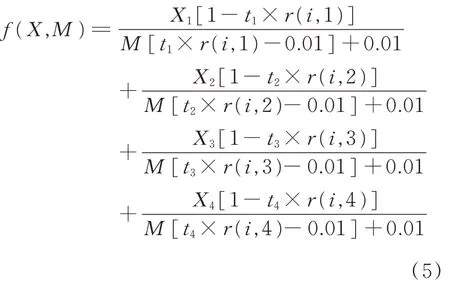
式中：t1、t2、t3、t4分別為紅、黃、藍、白植物染莫代爾纖維的修正系數。在擬合試驗過程中發現配色模型中的M變量在一定范圍內對配色擬合的結果影響不大，基于此，將固定配比的混紡色紗反射率、固定配比的數值、各組分的反射率數據以及預先擬合出的相近M值代入，獲得修正系數并進行式（6）的計算。

式中：i表示4種不同色紗（i=1，2，3，4），j表示第n個樣品，tij為同一種類型的組合下不同配比時所計算得到的各組分的修正系數，如t12為某一組合下第2個樣品反射率計算所得到的紅色修正系數，t1為最終所得到的對應組合下的紅色修正系數。首先使用未加入修正系數的原模型進行模擬配比，計算對應的M變量，將紗線實際配比與M變量代入式（5）中，經過計算機循環模擬，對比獲得此配比下擬合色差最小時的修正系數t1j、t2j、t3j、t4j，代入式（6）得t1、t2、t3、t4作為該組合類型的配色修正系數。例如：計算四色組合（R∶Y∶B∶W）的修正系數時，求得3∶2∶3∶2、3∶3∶2∶2、2∶3∶3∶2樣品下原模型時的3個M值，將M值與對應的配比代入式（5）求得t11、t21、t31、t41、t12、t22、t32、t42、t13、t23、t33、t43，將其代入式（6）得t1、t2、t3、t4，即R、Y、B、W配比組合的修正系數，此R、Y、B、W組合下的t1、t2、t3、t4分別為1.080、0.417、1.268、1.215。通過此方法計算所得不同組合下的修正系數見表2。

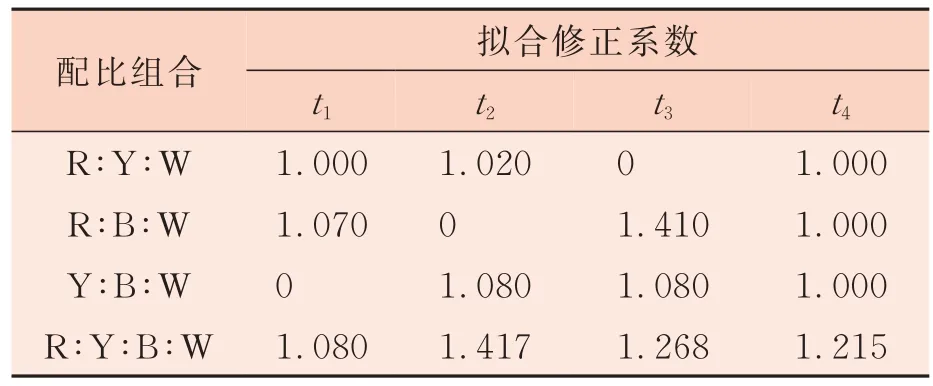
表2 不同組合下各組分修正系數

各組合的修正系數代入配色公式（5）中對各配色組合中其他配比的混紡紗進行修正配比擬合，得出表3修正后的模擬配比與誤差值，可進行各組合修正前后擬合的配比以及模擬配比與實際配比的誤差值對比。

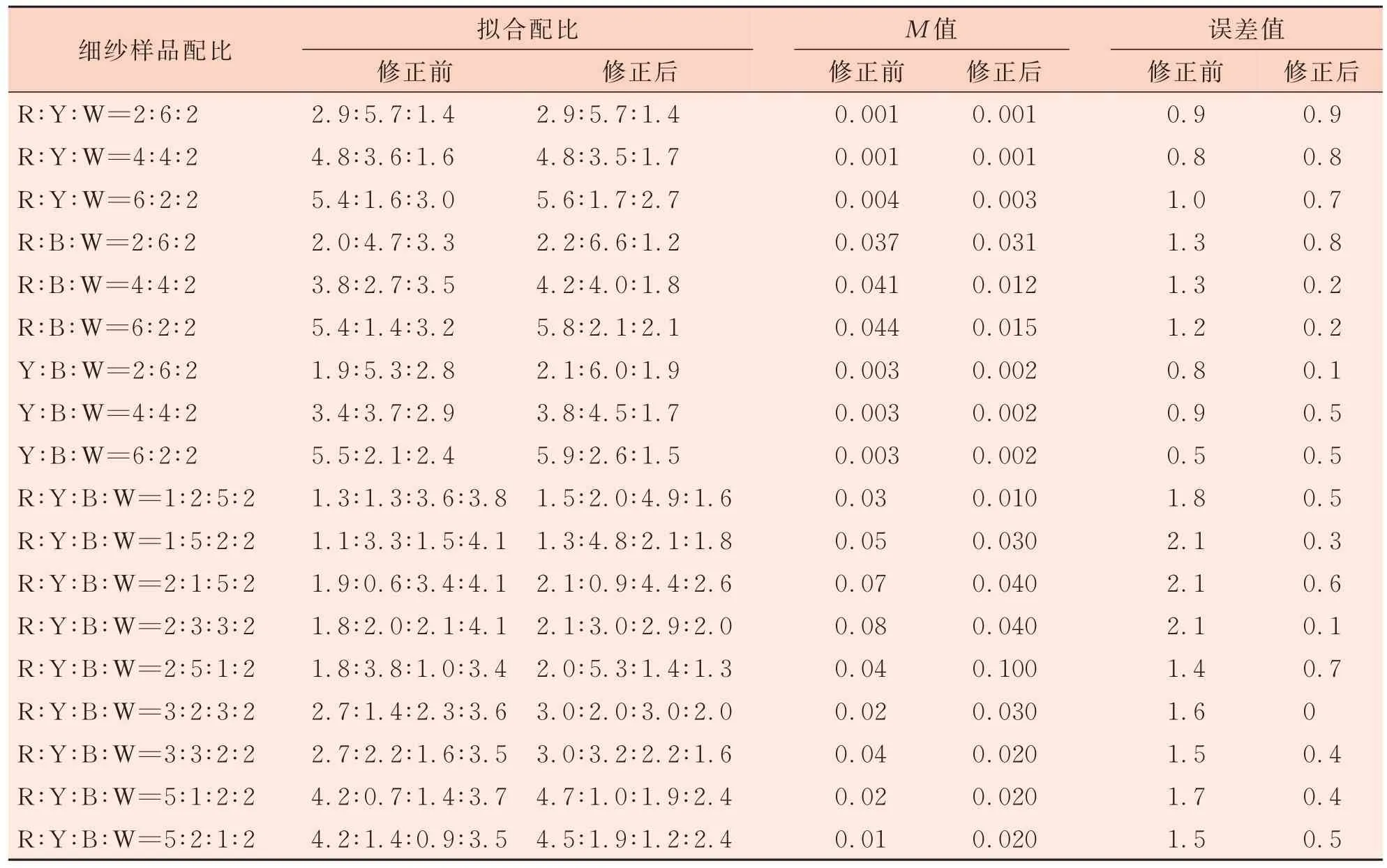
表3 修正前后細紗組分反射率配色模擬誤差對比

通過表3中修正前后模擬配比與實際生產配比的誤差值可以看出，原先紅、黃、藍配色與原配比的誤差值在1～2，經過修正后誤差值均縮小到1以內，在各組合中經過修正后的擬合配比與實際配比的誤差值相比于原擬合配比與實際配比的誤差值在整體上減小，尤其對于誤差值較大的組合更為明顯，因此修正后的擬合配比更加接近實際的配色比例，在實際配色中與原色紗的色差會更小。在同一組合下不同誤差值較為平穩，修正后部分擬合數據有較大的改進，說明在穩定生產條件下修正系數的添加對于同一配比組合具有明顯的修正效果。

2.3 試紡驗證

由配色模擬獲得較小的配比誤差值可初步實現精確穩定的配色模型，之后再根據未修正的模型與添加修正系數后的模型模擬的配比進行試紡，通過對修正前后試紡樣品與原樣的色差對比觀察實際生產上修正系數添加的效果。表4為部分第一次試紡的細紗與原配比混紡紗的色差對比。由于植物染料的色牢度與染色的不穩定性，在實際紡紗中紗線與目標顏色的色差要比化學染高，難以達到穩定的配色效果。由表4可以看出，經過修正后所紡的色紗與目標的色差小于原模擬配比與目標的色差，對于模擬配比在實際生產上有較大改進，修正模擬后在第一次試紡中色差的減小說明修正系數的添加對于實際生產具有積極的效果，可以有效減少實際生產中植物染色牢度的不穩定對配色模擬準確性的影響，平衡有關產生色差的各種影響因素，對于生產環境等問題帶來的嚴重配色差距有著明顯的效果，以便減少后續修色的次數而更加有利于實現生產目標。

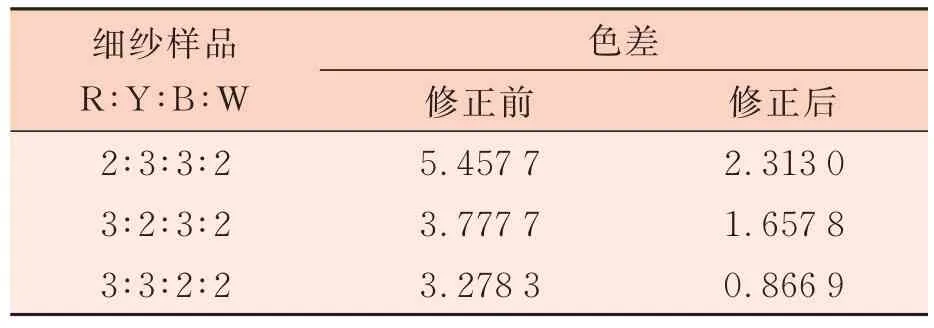
表4 修正前后第一次試紡色差對比

3 結論

在經過不同配色模型、樣品、比例等試驗與分析可得出以下結論。

（1）Stearns?Noechel模型在實際生產中具有優良的適應性、準確性和穩定性，可適應于色紗中多種不同組分組合的生產工藝；在棉網與細紗樣品中，由細紗所制成的樣品在配色方面更加準確和穩定。

（2）分類配色與修正系數可以在一定程度上減小不同色紡纖維間的相互影響產生的各組合間的配色準確性差距；修正系數的添加可以一定程度上減小色紡紗掉色等問題的影響，令數據的處理更加適應于實際生產情況。

（3）針對植物染色紡紗進行的配色模型處理是基于生產條件與原料穩定的情況下，減小實驗室中第一次試紡色差可以加速模擬到成品之間的流程，一定程度上改善植物染掉色嚴重等帶來的配色困難問題，對于植物染中原配比模型誤差較大的情況具有明顯的改善，不失為一種有效、便捷的修色方式。