塞罕壩華北落葉松人工林樹冠外部輪廓模型*
趙婷婷 王冬至,2 張冬燕,3 郭 立 黃選瑞,2
(1.河北農業(yè)大學林學院 保定 071000; 2.河北省林木種質資源創(chuàng)新與保護實驗室 保定 071000; 3.河北農業(yè)大學經濟管理學院 保定 071000; 4.豐寧千松壩林場 承德 068350)
樹冠是樹木進行光合作用、呼吸作用和蒸騰作用等一系列生理活動與環(huán)境進行物質交換和能量轉化的主要部位(李鳳日, 2004; 郭孝玉, 2013),其形狀和大小在生物多樣性、林木競爭(Crecente-Campoetal., 2009; Sadono, 2015)、光攔截(Stercketal., 2001)、碳估計(Gaoetal., 2017)、生產力及經營效果評價(Tanabeetal., 2001)等研究領域具有重要作用。樹冠外部輪廓是將每輪最大枝條的梢頭連接所構成的曲線,其不僅是樹冠形狀和大小的直觀表現(劉兆剛等, 1996; Hemeryetal., 2005),而且是研究樹冠表面積、樹冠體積的基礎以及模擬林分動態(tài)生長的依據(Jahnkeetal., 1965)。因此,構建樹冠外部輪廓預測模型,對了解樹木生長發(fā)育的動態(tài)變化規(guī)律有重要意義。
目前,國內外關于樹冠外部輪廓模型的研究已由簡單幾何形狀、分段函數等發(fā)展為比較靈活的可變指數方程,以冪函數(吳明欽, 2014)、修正Kozak方程(高慧淋, 2017; 高慧淋等, 2018)和修正Weibull方程(Ferrareseetal., 2015; Sunetal., 2017)等為主,多采用最小二乘法估計模型參數。最小二乘法要求模型殘差項滿足正態(tài)分布、方差齊性且獨立特性,由于枝條數據多具有時間相關性和空間異質性,因此需要發(fā)展新的方法來彌補這種不足。李春明(2009)、符利勇等(2012)研究表明,混合效應模型能夠有效解決以上問題,如部分學者基于非線性混合效應模型構建地位指數模型(Zangetal., 2016; ?z?eliketal., 2018; 符利勇等, 2011)、冠幅預測模型(Fuetal., 2017; Dongetal., 2016a; 2016b)、直徑生長模型(Bohoraetal., 2014)、心材預測模型(賈煒瑋等, 2018)等,結果均表明非線性混合效應模型預測精度更高。為了描述樹冠最大外部輪廓,Sun等(2017)基于分位數回歸模型構建了樟子松(Pinussylvestrisvar.mongolica)樹冠外部輪廓模型。分位數回歸可通過特定分位數構建多個分位數回歸方程,尋找因變量和自變量之間的關系,當因變量不同于條件均值時,分位數回歸優(yōu)勢顯著(Weiskitteletal., 2011),已在自疏邊界線模型(Zhangetal., 2005)、直徑分布模型(Meht?taloetal., 2008)、林分密度指數(Duceyetal., 2010)、直徑生長模型(Bohoraetal., 2014)構建等方面得到了大量應用。
在樹木生長過程中,冠形會受胸徑(diameter at breast height,DBH)、樹高(height of the tree,HT)、冠長(crown length,CL)、冠幅(crown width,CW)、冠高比(crown height ratio,CHR)、高徑比(height to diameter ratio,HDR)、林分年齡(stand age,Age)、林分密度(stand density,Sd)等多種樹木和林分因子影響(郭艷榮等, 2015; 高慧淋等, 2017; Doruskaetal., 1998),基于非線性混合效應模型和分位數回歸模型構建包含樹木和林分因子的樹冠外部輪廓預測模型是一個亟待解決的科學問題。本研究以河北省塞罕壩機械林場華北落葉松(Larixprincipis-rupprechtii)人工林為研究對象,利用冪函數、修正Kozak方程和修正Weibull方程選取適用于描述樹冠外部輪廓的最優(yōu)模型,通過相關分析確定影響樹冠外部輪廓的主要因子,采用非線性混合效應模型和非線性分位數回歸模型構建樹冠外部輪廓預測模型,并比較分析2種模型的預測精度,以期為準確預測樹冠生長發(fā)育規(guī)律及預估生產力提供科學依據。
1 研究區(qū)概況與數據來源
1.1 研究區(qū)概況
研究區(qū)位于河北省承德市塞罕壩機械林場(41°22′—42°58′N,116°53′—118°31′E),為陰山山脈與大興安嶺余脈的交界地帶,地勢北高南低,海拔1 010~1 940 m。屬華北暖溫帶氣候類型區(qū),年均氣溫-1.2 ℃,年均最高氣溫33.4 ℃,年均最低氣溫-43.3 ℃,年均降水量約452.2 mm,主要集中在6—8月,年日照時數2 548.7 h。土壤類型以褐色森林土、棕色森林土、砂壤土、壤土、風沙土、沼澤土、礫石土、草甸土為主,成土母質主要為坡積物、殘積物、沖積物、沉積物和風積物。主要喬木樹種有華北落葉松、白樺(Betulaplatyphylla)、云杉(Piceaasperata)、樟子松、山楊(Populusdavidiana)、油松(Pinustabulaeformis)、蒙古櫟(Quercusmongolica)等。
1.2 數據來源
2018年7—8月,在塞罕壩機械林場設置10塊華北落葉松人工林標準地(0.06 hm2),調查林分年齡(Age,a)、林分密度(Sd,tree·hm-2)、平均胸徑(mean DBH,cm)、平均樹高(mean HT,m)、平均冠幅(mean CW,m)和平均冠長(mean CL,m),統(tǒng)計結果見表1。按照等斷面積徑級標準木法將標準地內所有樹木分為3個等級,每個等級選擇2株標準木進行樹干解析(樣地9、10分為5個等級,每個等級選擇1株標準木),解析木伐倒前測量其胸徑(DBH)和冠幅(CW),伐倒后測量其樹高(HT),并將第一活枝高處定為冠基高度(height at the base of the crown,HBC,m)、冠長(CL)定為CL= HT- HBC、冠長率(crown length rate,CLR)定為CL與HT的比值,高徑比(HDR)定為HT與DBH的比值。樹冠按1 m為1個區(qū)分段進行枝解析,觀測枝條基徑(branch diameter,BD,mm)、枝條長度(branch length,BL,cm)、弦長度(branch chord length,BC,cm)、著枝角度(branch angle,BA,°)和著枝深度(depth into crown,DINC,m)等變量,共調查解析木58株和1 789個枝條數據。根據枝條各屬性通過三角函數關系計算梢頭處樹冠半徑(crown radius,CR,m)和相對著枝深度(relative DINC,RDINC,m),CR=BC·sinBA,RDINC=(DINC- BC·cosBA)/CL。對所有解析木,每輪選取1個最大枝條(半徑最大)作為構建樹冠外部輪廓的樣本,共672個最大枝條。每塊標準地隨機選取1株解析木作為檢驗樣本,其余解析木作為建模樣本,建模樣本與檢驗樣本樣木及枝條屬性因子統(tǒng)計如表2所示。
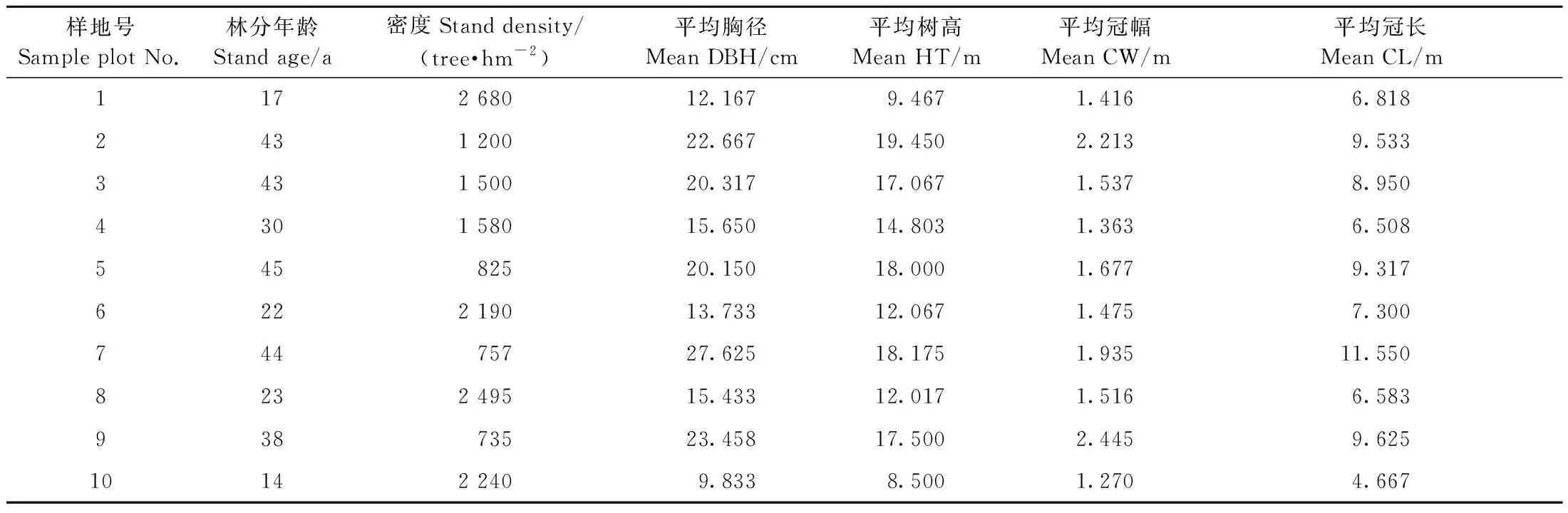
表1 華北落葉松人工林林分因子統(tǒng)計Tab.1 Statistics for stand variables of L. principis-rupprechtii plantation

表2 華北落葉松人工林解析木及最大枝條變量統(tǒng)計Tab.2 Statistics for attributes of sample trees and branch of L. principis-rupprechtii plantation
2 研究方法
2.1 基礎模型選擇
吳明欽(2014)利用可變冪函數方程擬合了杉木(Cunninghamialanceolata)樹冠外部輪廓; Ferrarese等(2015)利用修正Weibull方程擬合了美國黃松(Pinusponderosa)樹冠外部輪廓; Sun等(2017)通過對比冪函數方程、修正Kozak方程和簡單多項式方程對蒙古櫟樹冠外部輪廓進行了擬合。在描述樹冠外部輪廓的眾多模型中,冪函數、修正Kozak方程和修正Weibull方程(表3)是最常用的模型,因此本研究以冪函數、修正Kozak方程和修正Weibull方程作為構建塞罕壩華北落葉松人工林樹冠外部輪廓的基礎模型。

表3 基礎模型選擇Tab.3 The basic model selection
2.2 兩水平非線性混合效應模型
非線性混合效應模型是基于回歸函數依賴于固定效應和隨機效應的非線性關系而建立的回歸模型(符利勇等, 2015)。本研究考慮樣地和嵌套在樣地中樣木對樹冠半徑的影響,將樣地和嵌套在樣地中樣木作為隨機效應因子,構建嵌套兩水平非線性混合效應模型,形式如下:
(1)
式中:M為樣地數;Mi為第i塊樣地中嵌套樣木株數;nij為第i塊樣地中第j株樣木所測量樹冠半徑個數;yijk和vijk分別為第i塊樣地中第j株樣木第k次重復調查時因變量和自變量的觀測值;f(·)為樹冠外部輪廓基礎模型;β為p×1維固定效應參數;ui為q1×1維的第i塊樣地產生的隨機效應,假定服從期望為 0、方差-協(xié)方差矩陣為ψ1的正態(tài)分布;uij為q2×1維的第i塊樣地中第j株樣木產生的隨機效應,假定服從期望為0、方差-協(xié)方差矩陣為ψ2的正態(tài)分布;φijk為形式參數(簡稱形參),與β、ui和uij呈線性函數關系;Aijk、Bi,jk和Bijk分別為β、ui和uij的設計矩陣;εijk為隨機誤差項,假定服從期望為 0、方差為R的正態(tài)分布,并假定ui、uij和εijk誤差項之間相互獨立。
將所有參數及其組合作為隨機效應進行擬合,通過比較赤池信息準則(Akaike information criterion,AIC)、貝葉斯信息準則(Bayesian information criterion,BIC)和最大似然估計(maximum likelihood estimation,logLik),確定最優(yōu)隨機效應組合構造類型。對選取不同個數參數效應的最優(yōu)模型進行似然比檢驗,以約束模型中參數個數。樣地(樣木)內方差-協(xié)方差結構Ri如下:
(2)
式中:σ2為模型的殘差方差; Гi為樣地(樣木)內誤差相關性結構;Gi為描述方差異質性的對角矩陣。
采用冪函數(3)和指數函數(4)校正模型,以消除數據間的異方差性:
Var(eij)=σ2exp(2δvij);
(3)
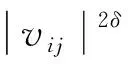
(4)
分別用復合對稱(complex symmetry)、對角矩陣(diagonal matrix)和廣義正定矩陣(general positive-definite matrix)表示樣地(樣木)內誤差相關性結構。
2.3 非線性分位數回歸模型
分位數回歸是Koenker等(1978)提出的,主要用于分析綜合響應變量(y)在各分位點與解釋變量(x)的關系。與最小二乘法相比,分位數回歸具有單調同變性及對異常值不敏感性,且在存在顯著異方差的情況下具有較強穩(wěn)健性(Cadeetal., 2003)。設隨機變量(x,y),y的分布函數如下:
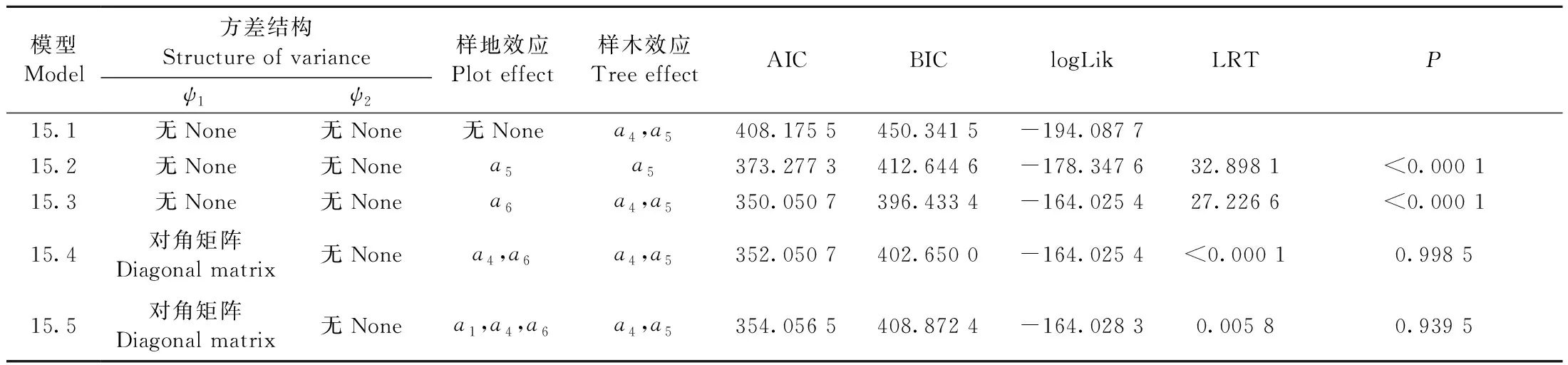
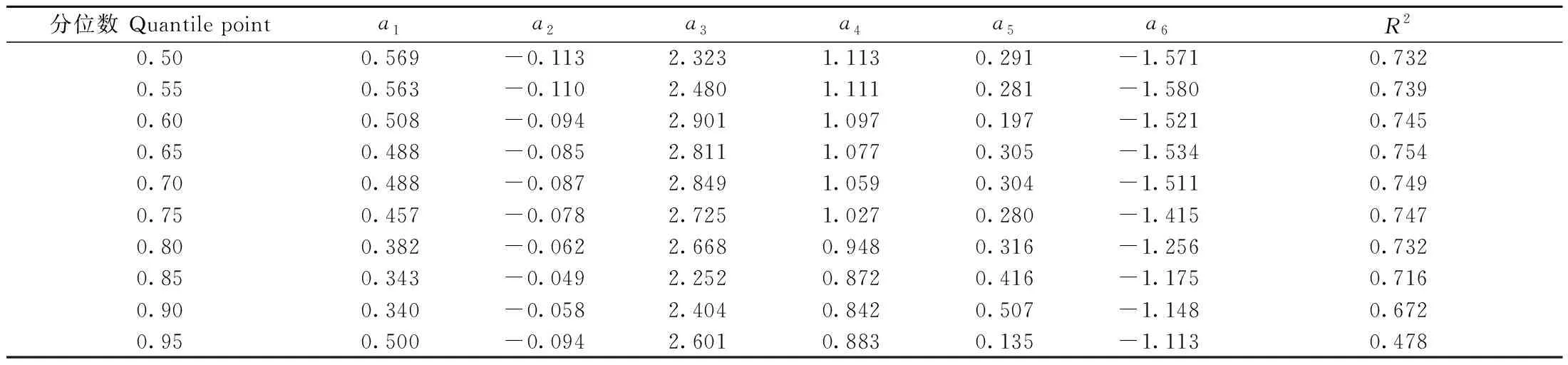
F(y)=P(Y (5) 對于任意分位數0 (6) 式中:F-1(q)為x的q分位點。 非線性混合效應模型如下: CRijk=f(X,θ)+εijk。 (7) 式中: CRijk為第i株樣木第j輪第k個枝條的半徑觀測值;f(X,θ)代表基礎模型形式;εijk為模型誤差項。 q選取不同分位點,代表不同分位點的估計值,通過反映不同分位點的數據趨勢,擬合參數估計結果。 任意分位點處各參數的估計值通過下式計算: (8) (9) 式中:NT、Ni、Nij分別代表樣木總株數、第i株樣木總輪數和第i株樣木第j輪枝條總數; 式(9)為損失函數。 Parente等(2016)研究證明,在線性回歸分位數中當誤差項存在組內相關但組間獨立時,分位數回歸估計值是一致并漸近正態(tài)的,漸近結果也可推廣到非線性分位數回歸,這為利用式(8)分位數估計值構建樹冠外部輪廓非線性分位數回歸模型提供了必要的理論基礎和經驗支持。Koenker等(1996)提出求解非線性分位數回歸模型的“內點法”,該方法于R語言quantreg軟件包中的nlrq函數得以實現(Koenker, 2019)。 采用赤池信息準則(AIC)、貝葉斯信息準則(BIC)、最大似然估計(logLik)、確定系數(R2)、均方根誤差(root mean square error,RMSE)、平均相對誤差(mean relative error,MRE)對模型擬合與檢驗結果進行評價。計算公式如下: AIC=-2LL+2p; (10) BIC=-2lnL+klnn= NlnSSE-nlnn+lnnp; (11) (12) (13) (14) 式中:p為模型參數個數; LL為最大似然函數的對數值; ln(n)為n的自然對數。 基于最小二乘法分別對冪函數、修正Kozak方程和修正Weibull方程進行擬合與評價(表4),結果發(fā)現冪函數均方根誤差(RMSE)、平均相對誤差(MRE)最小,確定系數(R2)較大,因此本研究選擇冪函數作為構建華北落葉松人工林樹冠外部輪廓的基礎模型。 設樹冠外部輪廓梢頭處樹冠半徑為0,且樹冠外部輪廓存在唯一拐點,MCR(maximum CR)和MRDINC(maximum RDINC)分別代表樹冠外部輪廓拐點處最大樹冠半徑和最大相對著枝深度位置。對MCR、MRDINC進行Pearson相關性分析(表5),結果發(fā)現MCR和MRDINC受林分年齡(Age)、冠長(CL)、胸徑(DBH)、樹高(HT)、冠高比(CHR)和高徑比(HDR)影響較大,其中MCR與Age、CL、DBH、HT、CHR呈正相關、與HDR呈負相關,MRDINC與Age、CL、DBH、HT、CHR、HDR均呈負相關。 表5 樹冠變量與影響因子的相關系數Tab.5 Correlation coefficient of crown variables with impacting factors respectively 基于描述樹冠外部輪廓的基礎模型及其主要影響因子,構建包含主要影響因子的非線性混合效應模型如下: (15) 混合效應模型擬合結果見表6,同時考慮樣木和樣地隨機效應的兩水平混合效應模型(15.3)比只考慮樣木效應的模型擬合效果好。在兩水平混合效應模型中,模型(15.3)AIC、BIC最小,且通過LRT檢驗,為參數較少的最優(yōu)混合效應模型。 表6 不同隨機效應組合混合模型擬合結果Tab.6 Fitting results of different random effects combined models 為了減小模型方差異質性,分別采用指數函數、廣義冪函數和冪函數消除模型異方差,不同方差函數混合效應模型擬合結果比較(表7)發(fā)現,加入方差函數的模型AIC明顯下降,表明樣地(樣木)效應并未完全消除數據間的異方差性,3種方差函數中冪函數表現良好,廣義冪函數與冪函數差異并不明顯,因此本研究選擇冪函數作為方差函數。模型估計結果如表8所示。 表7 不同方差函數混合效應模型擬合結果比較Tab.7 Fitting results comparison based on different variance functions 表8 混合效應模型擬合結果Tab.8 Mixed effects model fitting results 基于最大枝條數據對各分位點的非線性分位數回歸模型參數進行擬合(表9),隨著分位數增加,參數a1逐漸減小,a3先增大后減小再增大,a2、a5、a6逐漸增大,且所有參數估計值符號未發(fā)生改變,參數估計的穩(wěn)定性較強。利用0.50、0.55、0.60、0.65、0.70、0.75、0.80、0.85、0.90和0.95不同分位數模型模擬不同齡組樹冠外部輪廓(圖1),不同分位數樹冠外部輪廓曲線在0.50~0.95范圍內有較強的規(guī)律性,隨著分位數增大,樹冠外部輪廓曲線逐漸由樹冠中心位置向樹冠外側邊緣移動。除q=0.95分位數樹冠外部輪廓曲線明顯偏離樹冠外部輪廓邊界點外,0.50~0.90分位數樹冠外部輪廓曲線描述樹冠外部輪廓比較穩(wěn)定,總體趨勢一致。R2在分位數0.65~0.75時達到最大值,表明該范圍內分位數回歸模型能夠較好描述最大樹冠外部輪廓的平均變化趨勢,但并不能很好表示樹冠最大外部輪廓。在分位數0.50~0.90范圍內,隨著q增加,分位數模型曲線無限接近樹冠最大外部輪廓,相對于其他分位數,0.90分位數回歸模型最接近樹冠最大外部輪廓。 表9 分位數回歸模型擬合結果Tab.9 Quantile regression model fitting results 圖1 不同齡組華北落葉松人工林樹冠外部輪廓的分位數回歸曲線Fig. 1 The predicted crown profile for different age groups of L. principis-rupprechtii plantation by quantile models 基于混合效應模型和分位數分別為0.80、0.85、0.90、0.95的分位數回歸模型,利用檢驗數據對不同齡組華北落葉松人工林進行模擬。對比不同分位數回歸模型與混合效應模型擬合結果(圖2),混合效應模型樹冠外部輪廓曲線小于分位數回歸模型,且隨著q增加,分位數回歸模型樹冠外部輪廓曲線由樹冠中心位置逐漸向樹冠外側邊緣移動。q=0.95時,曲線偏離樹冠外部輪廓外側,q=0.90時,曲線最接近樹冠外部輪廓。當樹冠相對著枝深度小于0.7時,混合效應模型曲線與q=0.90時分位數回歸模型曲線均可較好描述樹冠外部輪廓,當樹冠相對著枝深度大于0.7時,混合效應模型曲線能夠更準確描述冠基處的平均外部輪廓,分位數回歸模型能更好顯示樹冠最大外部輪廓。 利用檢驗數據對混合效應模型和q=0.90分位數回歸模型在不同著枝深度處的殘差進行比較(圖3),混合效應模型和分位數回歸模型的殘差均接近0,混合效應模型有效描述了樹冠最大枝條的平均曲線,分位數回歸模型則準確確定了樹冠最大外部輪廓。 樹冠外部輪廓描述樹冠最外層樹冠邊緣的特征,與樹冠形狀和大小相關,是樹冠研究的重要內容 (Crecente-Campoetal., 2013; Stercketal., 2001)。高慧淋等(2018)以分段拋物線方程、修正Kozak和Weibull方程為基礎模型構建黑龍江省紅松(Pinuskoraiensis)和長白落葉松(Larixolgensis)樹冠外部輪廓模型,高慧淋等(2019)基于Kozak方程構建樟子松樹冠外部輪廓模型,樹種特征是決定樹冠形狀的主要因素,最適合描述其他樹種的模型可能并不適合描述華北落葉松人工林樹冠外部輪廓,因此,本研究從常見描述樹冠外部輪廓的模型中確定一個擬合效果較好的模型作為基礎模型,結果發(fā)現冪函數擬合華北落葉松人工林樹冠外部輪廓優(yōu)于修正Kozak方程和修正Weibull方程。Crecente-Campo等(2009)構建樹冠外部輪廓模型包含DBH、CL、HT等樹木因子,Baldwin等(1997)構建包含DBH、HT、CHR等樹木因子的二次多項式模型擬合火炬松(Pinustaeda)樹冠形狀,發(fā)現樹冠外部輪廓受不同樹木因子影響。Wang等(2016)提出除樹木因子外還應考慮林分因子對樹冠外部輪廓模型的影響,郭艷榮等(2015)基于不同齡組樣木數據構建樹冠外部輪廓模型,結果表明林分年齡對樹冠形狀有一定影響。因此,本研究通過對不同林分因子和樹木因子進行相關分析,將林分因子中的林分年齡(Age)以及樹木因子中的冠長(CL)、胸徑(DBH)、樹高(HT)、冠高比(CHR)和高徑比(HDR)加入模型中,提高了華北落葉松人工林樹冠外部輪廓模型擬合精度。 非線性混合效應模型能夠有效處理符合層次結構特點的數據,對提高模型精度具有顯著效應(李春明等, 2010; 符利勇等, 2012)。高慧淋等(2017)考慮單水平(樣地)效應構建樹冠外部輪廓混合效應模型,以DBH、CL、HDR對應參數作為隨機效應參數充分解釋了樣地內的變化。高慧淋等(2019)通過對比單水平(樣地或樣木)混合效應模型與兩水平混合效應模型,發(fā)現DBH對應參數同時考慮樣地和樣木效應,HDR、RDINC對應參數考慮樣木效應的兩水平混合效應模型優(yōu)于單水平(樣地或樣木)混合效應模型。本研究所用數據符合樣地-樣木-枝條層次結構,混合效應模型是處理該問題強有力的方法,對比樣木效應混合模型與樣地-樹木兩水平混合效應模型,兩水平混合效應模型可明顯改善模型擬合精度,當HDR對應參數考慮樣地效應,CHR、RDINC對應參數考慮樣木效應時,模型擬合效果最好。 分位數回歸不僅能夠描述樹冠外部輪廓的平均變化趨勢,而且還能得到任意分位點的樹冠外部輪廓 (Zangetal., 2016; ?z?eliketal., 2018),Sun等(2017)基于不同分位點建立樟子松樹冠輪廓模型,通過對比平均誤差和絕對誤差,確定q=0.95時分位數回歸曲線較接近樹冠輪廓。與Sun等(2017)研究方法一致,本研究利用0.50~0.95間隔為0.05作為分位點擬合華北落葉松人工林樹冠外部輪廓,除q=0.95分位數樹冠外部輪廓曲線明顯偏離樹冠外部輪廓邊界點外,0.50~0.90分位數樹冠外部輪廓曲線描述樹冠外部輪廓比較穩(wěn)定,且分位點為0.90時模型更適合描述華北落葉松人工林樹冠外部輪廓。精準預測樹冠外部輪廓是進一步研究樹冠表面積和體積的必要前提(Cadorietal., 2016; 吳丹子等, 2020),但樹冠外部輪廓會受到經營措施和空間競爭等因素影響(Wangetal., 2016; Garberetal., 2005),因此如何解決不同經營措施和空間競爭等因素對樹冠外部輪廓特征產生的影響還需進一步深入研究。 構建華北落葉松人工林樹冠外部輪廓模型時,冪函數為描述樹冠外部輪廓的最優(yōu)基礎模型,林分年齡、冠長、胸徑、樹高、冠高比、高徑比是影響樹冠外部輪廓的主要因子。同時考慮樣地和樣木效應的兩水平混合效應模型優(yōu)于樣木效應的單水平混合效應模型,可明顯提高模型擬合精度,精確描述樹冠外部輪廓的平均趨勢。除研究條件均值外,分位數回歸模型可靈活表示不同分位點樹冠外部輪廓,對樹冠外部輪廓邊界研究具有重要意義。2.4 模型評價與檢驗
3 結果與分析
3.1 基礎模型確定
3.2 影響樹冠外部輪廓的主要因子

3.3 兩水平非線性混合效應模型構建


3.4 非線性分位數回歸模型構建
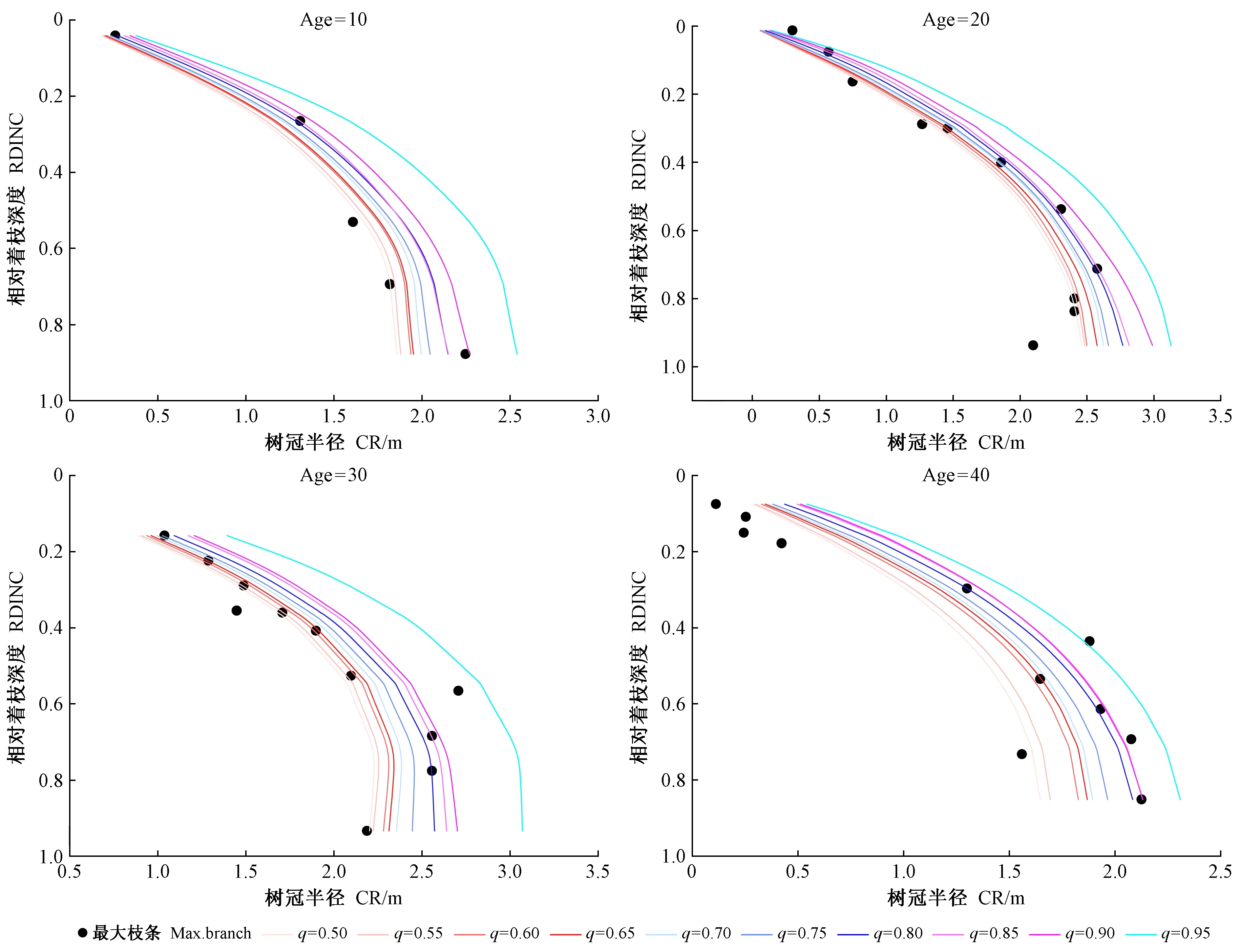
3.5 樹冠外部輪廓模擬
3.6 模型評價與檢驗
4 討論
5 結論

