變形態2219鋁合金高溫塑性變形的本構模型

王清松，徐戊矯，吳道祥，何珞玉，謝 丹

（1.西南鋁業(集團)有限責任公司，重慶 401326；2.重慶大學，重慶 400040）

0 前言

2219鋁合金屬于Al-Cu-Mn系合金，因其具備較好的高低溫力學性能、焊接性能、斷裂韌性和抗應力腐蝕性能而在工業與航空航天領域得到了廣泛的應用[1]。在2219鋁合金的環件軋制過程中，不恰當的鍛造或者加熱溫度都易造成合金中粗晶的形成，而且較快的變形速率容易使加工硬化速度大于再結晶速度，變形抗力增大。此外，較高的應變速率產生的溫度升高也會引起粗晶的出現，增加變形的不均勻性[2]。因此研究2219鋁合金在不同的變形溫度和應變速率范圍的流變行為很有必要。

國內外學者對于建立2219鋁合金的本構模型進行了一定研究。Sellars[3]提出了用含Z參數的雙曲正弦模型來描述材料的流動行為。HE[4]等用該模型建立了鑄態2219鋁合金的本構模型。但是，該模型并沒有考慮應變對流動應力的影響，因此要更準確地描述2219鋁合金的流動特性就必須考慮應變。由于變形態2219合金適用于環件軋制，這一過程的變形溫度在420～500℃、應變速率在0.25～0.8 s-1范圍內，因此本文在此變形溫度和應變速率為范圍內對變形態2219鋁合金進行壓縮試驗。研究其流動應力規律，建立修正之后的基于應變補償的雙曲正弦本構模型，為制定變形態2219鋁合金的環件軋制工藝提供理論依據。

1 實驗材料與方法

材料為變形態2219鋁合金，其化學成分如表1所示。試樣加工成直徑8 mm、高度為12 mm的圓柱試樣，柱面和端面粗糙度分別為Ra1.6和Ra0.8。試驗設備是Gleeble-3500型熱物理模擬試驗機。由于試驗需要考慮到具體環件軋制情況下的溫度和應變速率的范圍，因此根據實際的軋制條件（變形態2219鋁合金的高溫塑性變形溫度為420～500℃），選取420、460、500℃三個溫度，應變速率選定0.25、0.525和0.8s-1。以5℃/s的速度將試樣加熱到試驗溫度，保溫3 min后根據既定的應變速率進行壓縮，總應變為0.6。

2 實驗結果與分析

2.1 真應力-真應變曲線

圖1是實驗測得的不同溫度和應變速率下的真應力-真應變曲線。從圖中可知，同一應變速率下，真應力隨著溫度的升高而降低。因為溫度越高，原子間的結合力減小，原子的動能增大，位錯交滑移和攀移更容易發生，位錯密度降低，合金軟化，應力降低。從圖1（a）可知，隨著應變增大，應力急劇增大至峰值后慢慢減小然后基本保持恒定。原因是變形初期加工硬化起主導作用，隨著變形程度的增大，發生一定程度的動態再結晶，即動態軟化抑制了部分加工硬化，因此應力減小；當加工硬化和動態軟化達到平衡時，流動應力就基本保持恒定。在同一溫度下，真應力隨應變速率的增加而升高，如圖1所示。這是由于變形速率高時，變形時間減少，使動態回復過程不能充分完成，所以流動應力增大。

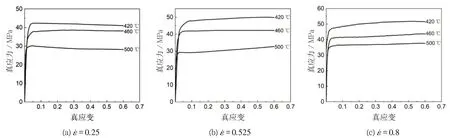
圖1 變形態2219鋁合金的真應力-真應變曲線

2.2 本構模型

在材料的高溫塑性變形過程中，應力和溫度、應變速率之間的關系用Zener-Hollomon參數（Z參數）[5]表示：

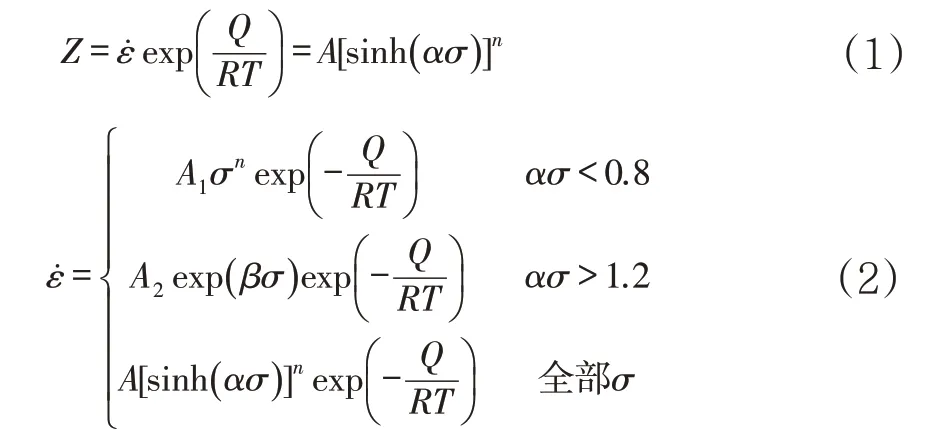
式中：˙為應變速率；Q為熱激活能；R為氣體常數；T為變形溫度；σ為流動應力；A1、A2、A、n、α、β為材料常數。

由公式（1）可以推出：

由雙曲正弦函數的定義：

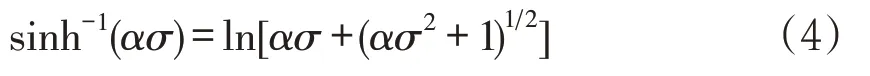
結合公式（3）、（4）求解得到本構方程為：

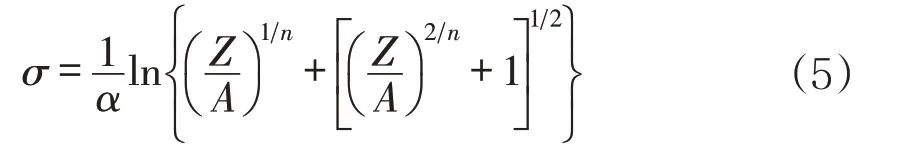
由公式（1）和（5）可知，只要知道A、n、α、Q等參數，就可以求出材料在任意變形條件下的流動應力。但從圖1可以看出，應變對流動應力也有一定的影響，公式（1）和（5）并沒有考慮應變。分析應變對流動應力的影響主要考慮應變對材料參數的影響，因此在建立本構模型時需要對獲得的材料參數進行應變補償，即得到各參數與應變的關系。

下面以應變為0.1為例，得到各材料參數。對公式（2）中低應力和高應力兩個方程兩邊取對數得到：

將圖1中應變為0.1時不同溫度下的應變速率和流變應力數據代入公式（6）和（7）中，分別做出ln˙-lnσ和ln˙-σ的關系圖，再用最小二乘法線性擬合就得到圖2所示的線性關系。

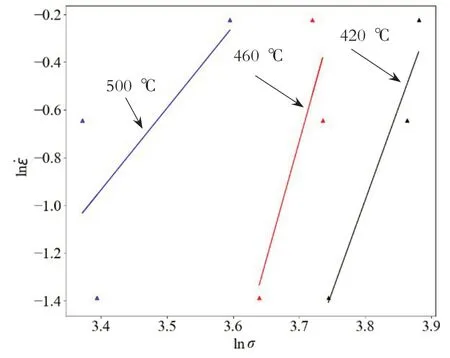
圖2 變形態2219鋁合金ln˙和ln σ關系圖

圖2對中三條直線的斜率求得平均值為n1=7.019；圖3中對三條直線斜率求平均值得β=0.175，求出α=β/n1=0.024912。

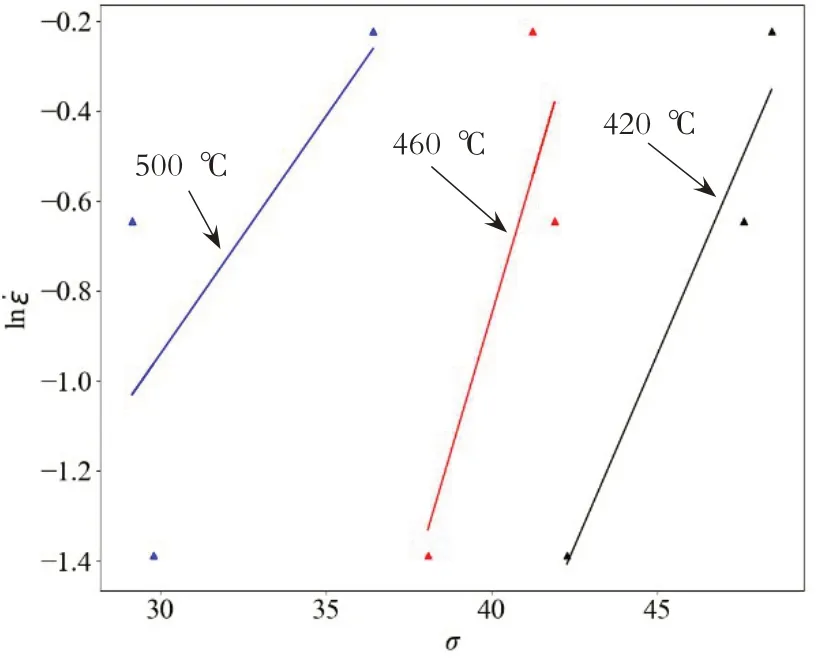
圖3 變形態2219鋁合金ln˙和σ關系圖

對公式（2）中全應力下，當溫度保持不變時，方程兩邊取對數得到：

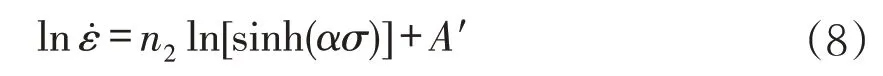
當應變速率保持不變時，對公式（2）兩邊取對數得到：

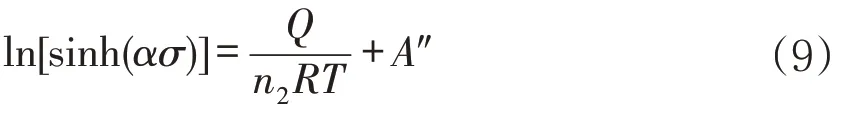
將不同溫度下的數據代入公式（8）、不同應變速率下的數據帶入公式（9），分別畫出ln˙-ln[sinh(ασ)]、ln[sinh(ασ)]-1/T圖，經過線性擬合得到圖4和圖5。求出圖4三條直線的斜率平均值n2=11.370，圖5三條直線斜率的平均值Q/n2R=3256.914，計算得到Q=143.874 kJ/mol。

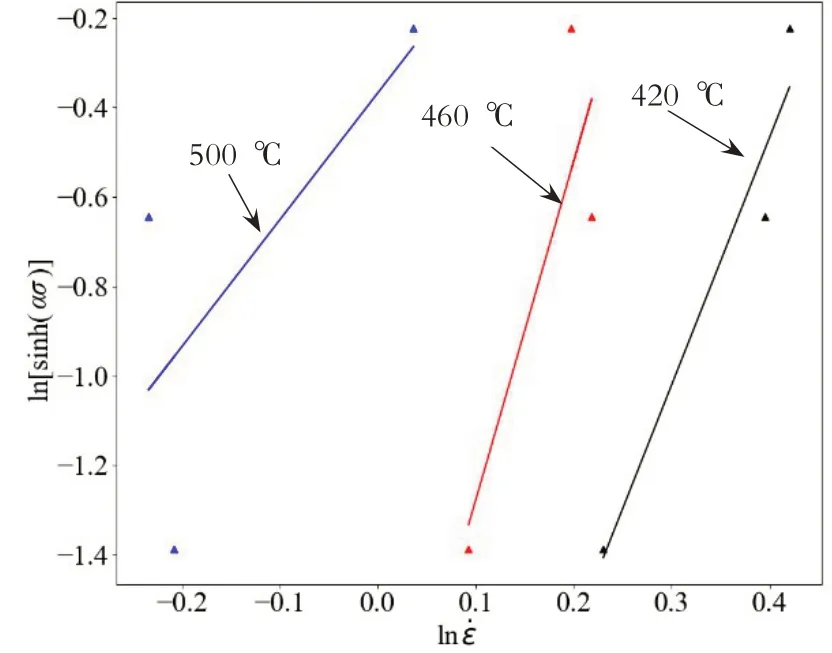
圖4 變形態2219鋁合金ln˙和ln[sinh(ασ)]關系圖

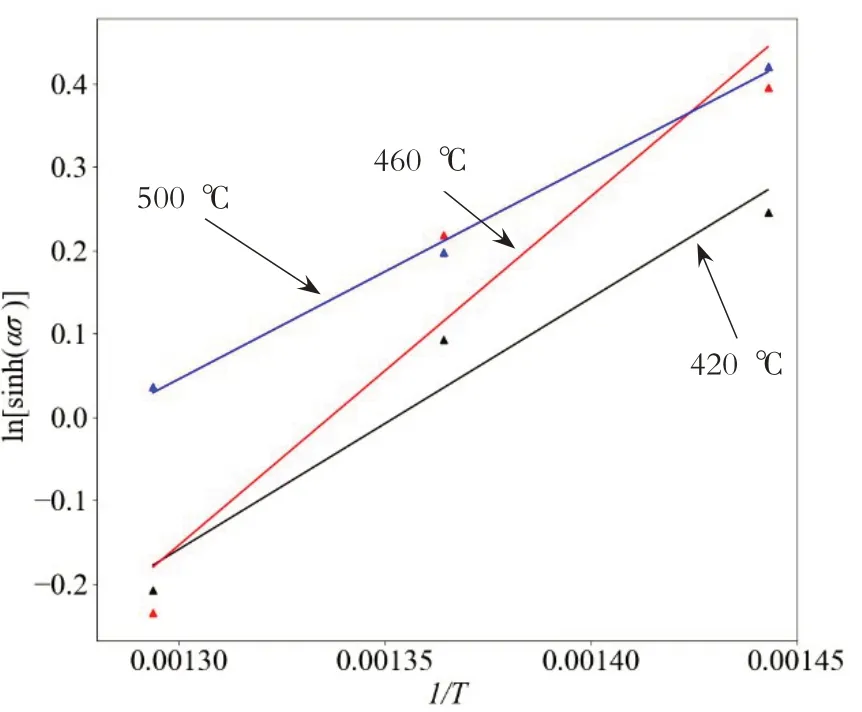
圖5 變形態2219鋁合金ln[sinh(ασ)]和1 T關系圖

對公式（1）兩邊取對數得到：

將上面算出的參數值和相關數據代入，畫出lnZ-ln[sinh(ασ)]圖，擬合出如圖6所示線性關系曲線；曲線的斜率n=5.073，截距lnA=21.960，A=3.444×109。至此得到了應變為0.1時的材料參數值，見表2。

表2 應變0.1時的材料參數

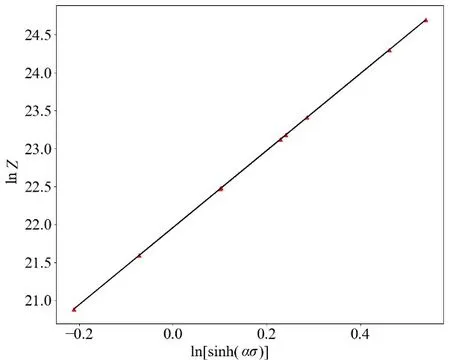
圖6 變形態2219鋁合金ln Z和ln[sinh(ασ)]關系圖

重復上述步驟，計算得到0.1、0.2、0.3、0.4、0.5、0.6不同應變值下的材料參數，并采用五次多項式（11）擬合，得出材料參數A、n、α、Q與應變的關系。

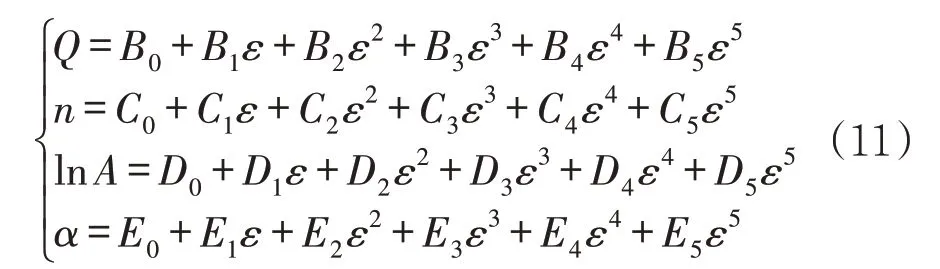
公式（12）為基于應變補償而建的2219合金雙曲正弦本構模型。圖7是2219鋁合金各材料參數的應變補償曲線，擬合出的多項式系數見表3。

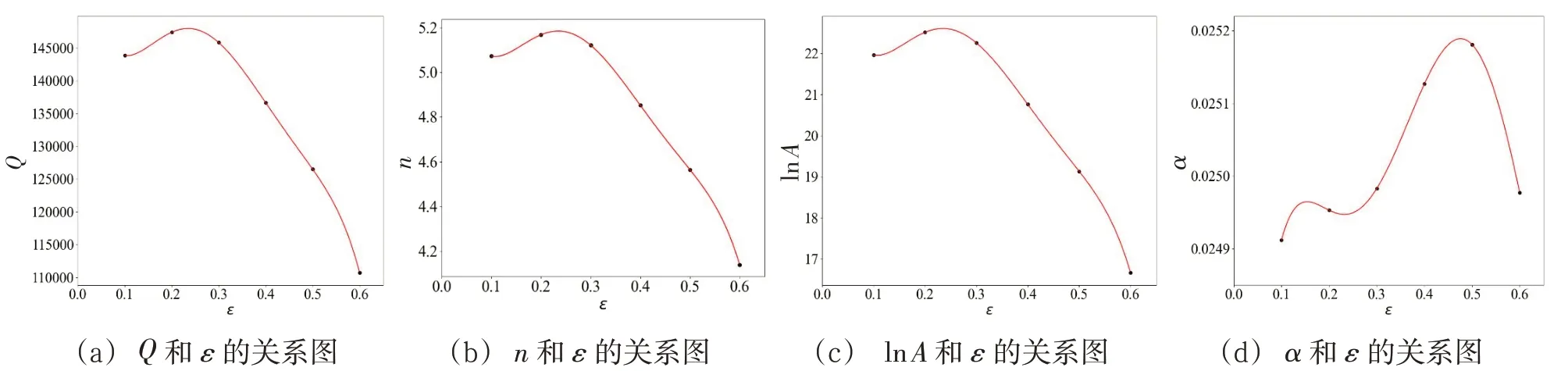
圖7 變形態2219鋁合金材料參數與應變的關系

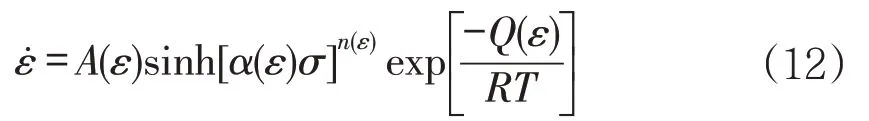
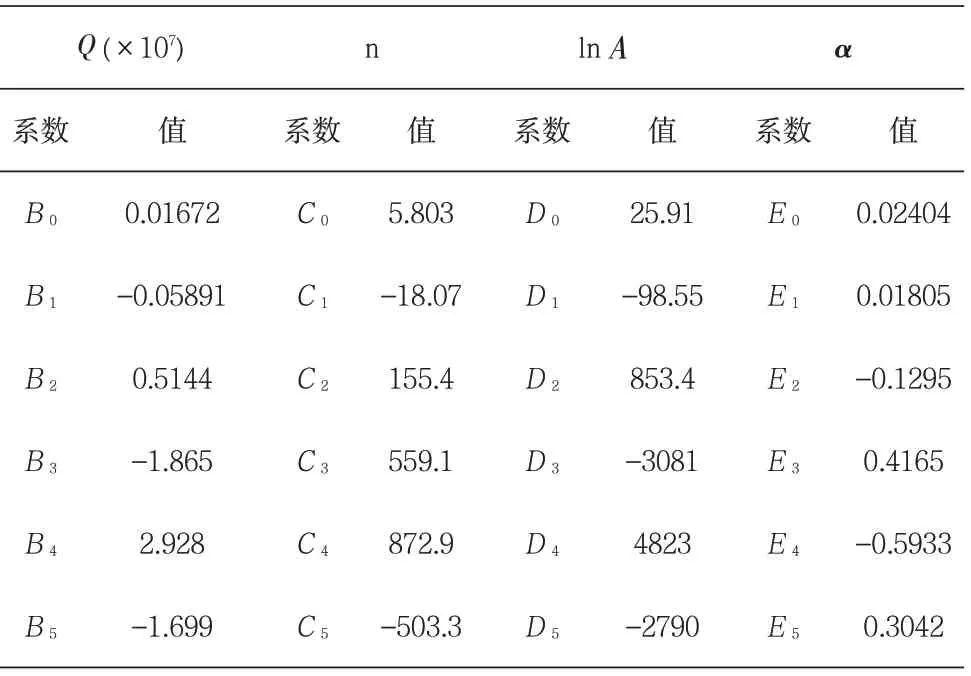
表3 變形態2219鋁合金材料參數的應變補償系數

2.3 模型驗證

分別取0.1、0.2、0.3、0.4、0.5、0.6應變值代入公式（12）中，計算得出不同變形下的流動應力，并與試驗數據做對比，如圖8所示。可以看出，計算得出的數據與試驗的數據吻合較好。根據誤差計算得出應力的計算值與試驗值的平均相對誤差為4.56%，說明該方程的準確性較高。

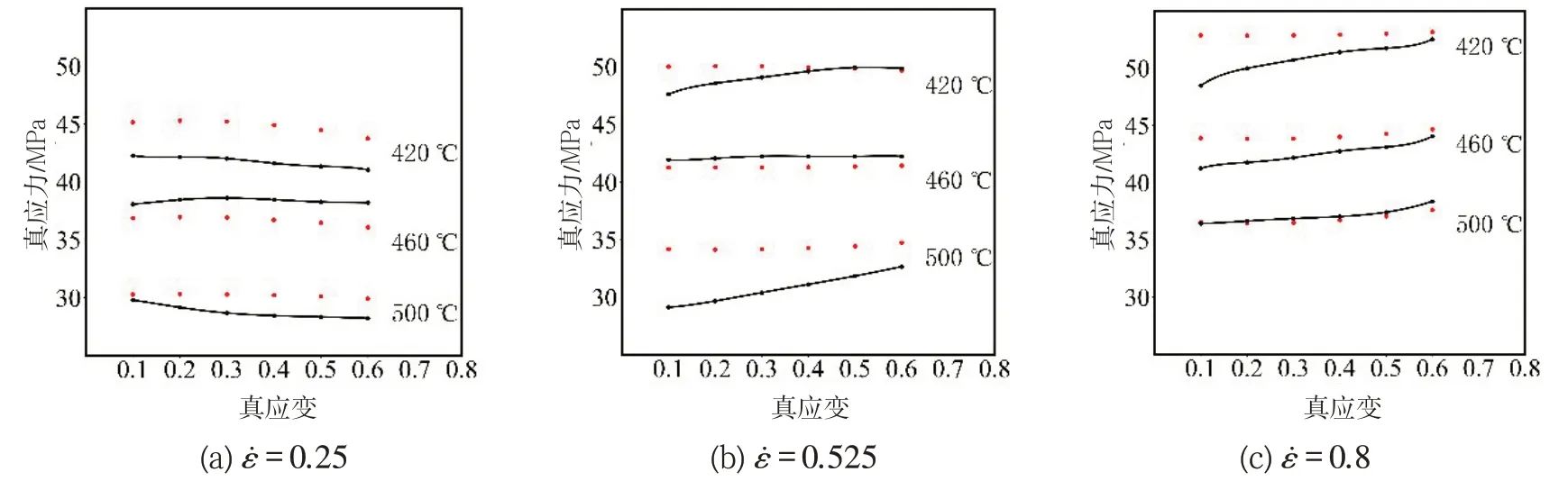
圖8 變形態2219鋁合金流動應力預測值和實驗值對比

3 結論

（1）變形態2219鋁合金的流動應力受應變速率和溫度的影響較大，隨著溫度的降低而升高，隨著應變速率的升高而升高。而且在變形過程中會出現應力急劇增大至峰值后慢慢減小然后基本保持恒定。其原因在于變形初期加工硬化起主導作用，隨著變形程度的增大，發生了一定程度的動態再結晶。

（2）基于應變補償建立了變形態2219鋁合金的雙曲正弦本構模型，并且應力的計算值與試驗值的平均相對誤差為4.56%。這說明該方程有較高的準確性，能較好地預測變形態2219鋁合金的高溫流變行為。