多相環形無刷勵磁系統的運行特性分析

郝亮亮， 胡啟昊， 張揚， 任仰凱， 宗衛晶， 汪南華

(1.北京交通大學 電氣工程學院，北京 100044；2.南京南瑞繼保電氣有限公司，南京 211102；3.陽江核電有限公司，廣東 陽江 529941；4.福建寧德核電有限公司，福建 寧德 355200；5.廣西防城港核電有限公司，廣西 防城港 538001)

0 引 言

我國核電經歷了長期發展，如今進入了核電重啟時期[1]，核電在電力結構中的比重逐年增大[2-3]。同步發電機勵磁系統作為核電發電系統中的重要組成部分，其性能對系統的穩定性和可靠性有很大的影響。隨著核電發電機組容量不斷增大，勵磁容量也不斷提高，大容量勵磁系統的可靠性和安全性受到了人們的關注[4]。國內外學者對大容量發電機組勵磁系統的發展和優化進行了大量的研究，提出了種類繁多的勵磁系統[5]，其中無刷勵磁系統明顯提高了勵磁系統的可靠性，保障了發電系統的穩定和安全，具有廣闊的發展前景。

相較于有刷勵磁系統，無刷勵磁系統消除了勵磁機的碳刷和滑環，減小了勵磁系統的維護工作量，顯著提高了發電機勵磁系統的可靠性[6]。特別在高濕度的空氣中或者具有腐蝕性的介質中等惡劣的環境條件下，無刷勵磁系統具有良好的耐腐蝕性，被廣泛應用于船舶動力[7]、水力發電[8]、核電[9]等領域。同時無刷勵磁系統還具有勵磁響應快、維護成本低、制造過程簡單、可靠性高等顯著優點。

為了提高無刷勵磁系統的可靠性，國內外學者對無刷勵磁系統的特性進行了大量研究，其中大部分是針對經典的三相無刷勵磁系統[10-13]。在三相無刷勵磁系統的基礎上逐漸發展出六相[14]、九相[15]、十二相[16]等多相無刷勵磁系統，明顯改善了勵磁機性能，減小了高次諧波電流，提高了整流電壓的品質。近年來出現了大容量多相環形無刷勵磁機，大大提升了系統的容錯性和可靠性，十一相、三十九相和四十六相等多種機型[17]被廣泛應用在核電無刷勵磁系統中，我國的紅沿河和寧德等核電站均采用多相無刷結構。多相環形無刷勵磁機的相關設計原理目前仍是國外某公司的商密，未見公開資料進行討論。而系統運行特性的分析是進行設計及優化的關鍵。近年來，專家學者們對多相環形無刷勵磁機的勵磁繞組故障[18]、電樞繞組短路故障[19]以及二極管開路故障[20]的特征進行了大量的研究，但是未見有文章對其運行特性進行分析。

應用于艦船、航空和電動汽車等場合的電機也有采用類似環形繞組的結構，可為本文的研究提供借鑒。文獻[21]介紹了一種新型直流電動機電樞電路，重點研究了換向單元自感、互感對機械特性的影響，但并未對整流系統的各種電氣量進行分析計算。文獻[22]提出了一種用于混合勵磁發電系統的新型無刷勵磁機，并對無刷勵磁機的運行機理和電磁性能進行了分析。文獻[23]和文獻[24]則分別介紹了五相永磁電機的容錯策略和多相環形繞組無刷直流電機的換向過程分析及建模方法。另外，專家學者們也提出了其他相數的直流無刷發電機模型[25]和異步電機模型[26-27]，并對系統在各種整流模式下的模型進行了改進和優化[28]。

為了研究多相環形無刷勵磁系統正常運行特性，本文以11相環形無刷勵磁機及旋轉整流系統為研究對象，通過分析系統結構特征，總結其工作原理及運行特性，同時建立實際工作狀態下的數學模型，提出整流系統仿真與解析計算方法，并在旋轉磁極式的勵磁機動模樣機上進行實驗，驗證模型及計算方法的正確性，為分析新型大容量無刷勵磁系統的實際運行特性提供工程設計上的指導，也為其在拓撲結構上的創新奠定基礎。

1 多相無刷勵磁系統的工作原理

圖1為11相環形無刷勵磁機及旋轉整流系統的示意圖，其交流側的每一相電樞繞組被等效為一個理想的正弦電壓源e和一個等值電感Lγ的串聯。各相電樞繞組依次首尾相連形成一個環形回路，每一相電樞繞組兩端各接一對反向并聯二極管，構成11相全波整流電路。該勵磁機為旋轉磁極式凸極電機，與實際運行的旋轉電樞式電機有所不同。由于轉極式結構不影響發生在定轉子間的電磁關系，且便于實驗中電樞及勵磁側電氣量的測量以驗證分析，因此在分析和實驗中都采用了轉極式設計方案。

圖1 11相環形無刷勵磁機及旋轉整流系統示意圖Fig.1 Schematic diagram of 11-phase annular brushless exciter and rotatory rectifier system

該轉極式11相無刷勵磁機極對數為5，定子槽數為77，電樞繞組在定子上均勻分布，相鄰兩相間相差8π/11機械角度，即40π/11電角度。根據電樞繞組內電勢相位的特點，可以得到圖2所示的電樞繞組內電勢相量圖，并得到每相內電勢

圖2 電樞繞組內電勢Fig.2 Internal electromotive force in armature windings

n=1,2,…,10,11。

(1)

式中：E為電樞繞組內電勢的有效值；ω為同步轉速；n為電樞繞組相數。

基于二極管的導通模式以及11相環形無刷勵磁機及整流系統的結構特點進行分析，可得n相電樞繞組內電勢串聯表達式為

(2)

由式(2)計算可知，3相或8相(8相即為11減3相)電樞繞組串聯可取得最大的電壓幅值，因此上下橋臂導通的二極管之間應保持三相電樞繞組串聯。三相串聯的電壓波形如圖3所示，相鄰波形相差π/11電角度。

圖3 三相串聯電樞繞組的電壓波形Fig.3 Voltage waveforms of three armature windings in series

由于11相環形無刷勵磁機及旋轉整流系統換相二極管之間始終保持三相電樞繞組的串聯，而其交流側有11相電樞繞組，在實際運行中交流側電樞繞組分成4條支路并聯為負載側供電，其等效電路如圖4所示。

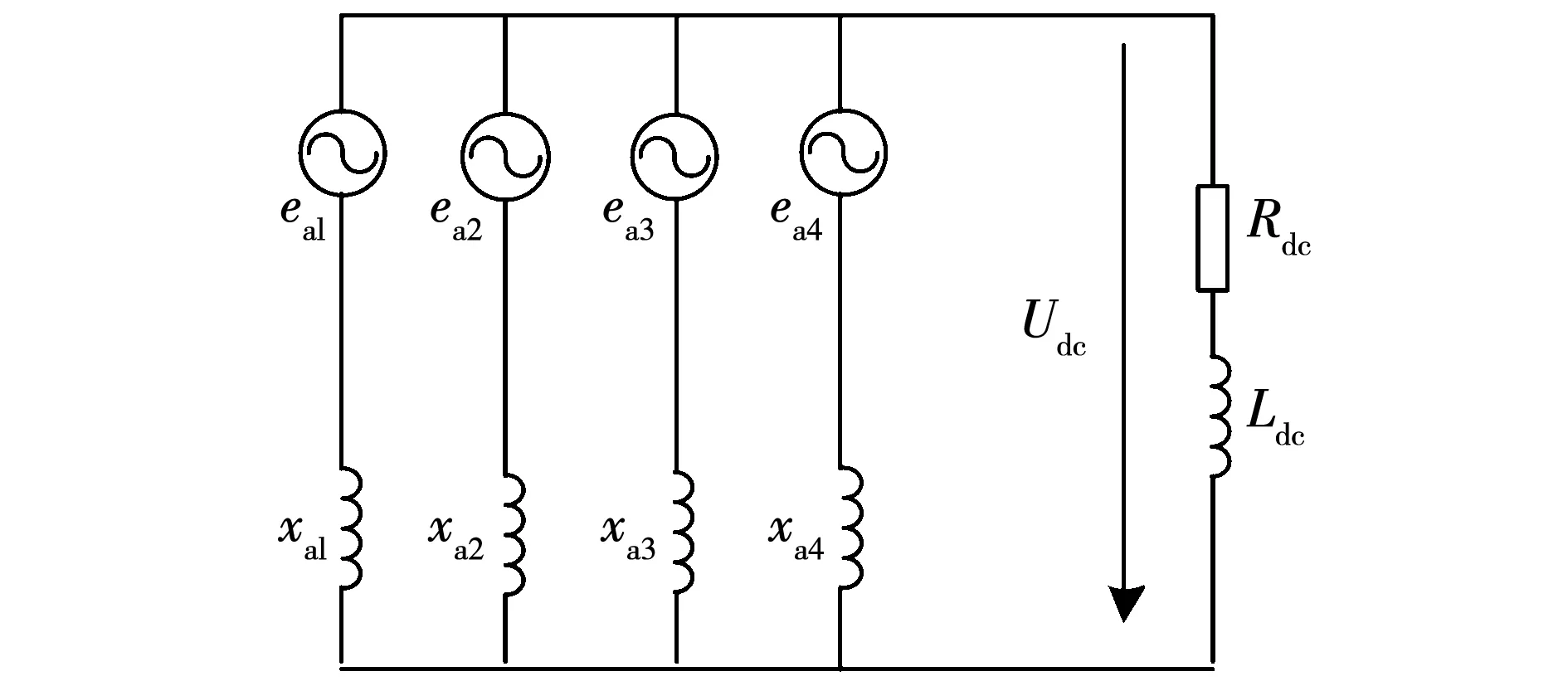
圖4 工作狀態時整流器的等效電路Fig.4 Equivalent circuit of the rectifier in working condition

在實際運行中，交流側電樞繞組存在電感，二極管存在換相過程，此時電樞電感中因電流變化產生的反電勢將與勵磁機勵磁電流產生的內電勢一起共同影響多相旋轉整流橋的運行狀態。

由于運行中的換相過程十分復雜，將首先建立系統的數學仿真模型，在經過動模機組實驗驗證仿真模型的正確性后，再采用該模型計算并分析實際多相無刷勵磁系統的運行特性。

2 多相無刷勵磁機及旋轉整流系統的數學模型

以一般m相環形無刷勵磁機為對象，建立其數學模型。

2.1 勵磁機定子勵磁繞組方程

電壓方程為

ufd=pψfd+rfdifd。

(3)

式中：ufd為勵磁機的勵磁電壓；p=d/dt為微分算子；ψfd、rfd和ifd分別為定子磁鏈、電阻和電流。

無刷勵磁機的定子和轉子繞組均會在定子勵磁繞組中產生磁鏈，因此定子磁鏈方程為

(4)

式中：Lfd為定子繞組的自感；Mri,fd為定子繞組與第i相轉子繞組的互感；iri為第i相轉子繞組的電流。

以電流為待求量，由式(3)和式(4)可得勵磁機定子勵磁繞組方程為

(5)

2.2 勵磁機轉子繞組方程

勵磁機轉子第i相繞組的電壓方程為

uri=pψri-rriiri。

(6)

式中：uri為勵磁機第i相繞組的電壓；ψri、rri和iri分別為轉子磁鏈、電阻和電流。

同樣地，無刷勵磁機的定子和轉子繞組均會在轉子電樞繞組中產生磁鏈，因此轉子磁鏈方程為

(7)

以電流為待求量，由式(6)和式(7)可得勵磁機轉子電樞繞組方程為

(8)

2.3 勵磁機的直流負載方程

勵磁機的轉子電樞繞組經旋轉整流橋給發電機的勵磁繞組供電，因此勵磁機的直流負載為發電機的勵磁繞組，其電壓方程為

(9)

式中：udc為直流負載電壓，即發電機的勵磁電壓；Ldc、rdc和idc分別為勵磁繞組的電感、電阻和電流。

2.4 系統的總方程

將式(5)、(8)和(9)合并，形成多相無刷勵磁機及旋轉整流系統的總方程，為便于理解寫出矩陣形式為

(10)

簡化的矩陣方程形式為

U=p(MI)+RI。

(11)

其中：U、M、I和R分別為多相無刷勵磁機的電壓矩陣、電感矩陣、電流矩陣及電阻矩陣。

2.5 考慮多相整流橋實際狀態的標準方程

事實上，式(11)沒有反映出勵磁機轉子電樞繞組和負載之間通過旋轉整流器的實際連接，可通過電路的關聯矩陣細致描述其連接關系。由前文分析可知，11相環形勵磁機正常運行時，相鄰3相繞組串聯導通，換相過程中出現多個二極管支路導通的情況，此處以圖5所示的狀態為例，電樞繞組r1、r2、r3串聯導通，換相過程中二極管D1、D3、D5和D8、D10處于導通狀態，其余二極管處于關閉狀態。

圖5 形成關聯矩陣的示意圖Fig.5 Schematic diagram of forming an incidence matrix

圖5中有6個獨立換相回路，在定義了元件和回路的參考方向后，可以得到關聯矩陣為

(12)

其中：fd表示勵磁支路；r1,r2，…，rm表示電樞繞組支路；dc表示直流負載支路；負號代表與圖中參考方向相反。

通過關聯矩陣對電路的電壓和電流進行變換：

U′=BU；

(13)

BTI′=I。

(14)

將式(13)、式(14)代入式(11)得

pI′=-M′-1(pM′+R′)I′+M′-1U′。

(15)

其中：M′=BMBT；R′=BRBT。

式(15)即為考慮多相整流橋實際運行狀態的標準矩陣方程，其中各電感參數可以采用多回路分析法[29]進行計算，不再贅述。求解該方程，即可求得不同狀態下系統的電壓和電流。

3 實驗與仿真

3.1 動模實驗系統

由于實際大容量電機不具備實驗條件，基于實際11相環形無刷勵磁機及其整流系統，設計了一臺動模樣機，該樣機與實際無刷勵磁機除了容量大小的區別之外，槽數、極對數、電樞繞組聯接方式等完全一致。為了方便電樞繞組及二極管電流、電壓的測量，樣機采用的是轉極式設計方案，其基本參數如表1所示。

表1 實驗樣機基本參數

實驗系統圖如圖6所示。實驗過程中用直流電動機拖動實驗樣機旋轉，直流電動機由直流調速器驅動，并引入轉速閉環控制以保持實驗樣機轉速不變。開關直流電源為實驗樣機的勵磁繞組提供恒定的直流電流，各電樞繞組首端經整流器與負載相連。

圖6 實驗系統圖Fig.6 Diagram of experiment system

3.2 實驗與仿真結果對比

實驗過程中，將直流電源的電壓設置為10 V，原動機拖動實驗樣機勻速旋轉，轉速恒定960 r/min，即電樞感應電勢基波頻率為80 Hz(周期為0.012 5 s)，用錄波儀記錄下正常運行過程中相關電氣量波形，采樣頻率為50 kHz，負載電阻為10.6 Ω，負載電感為0.357 H。實驗和仿真結果的對比如圖7所示，波形基本一致，驗證了建立的模型的準確性。

從圖7(c)和(d)可以看出，多相無刷勵磁機的電樞電流波形出現了明顯的畸變，同時二極管電流的波形也是不連續的。這是由于整流器復雜的換相過程以及特殊的環形結構連接所決定的。

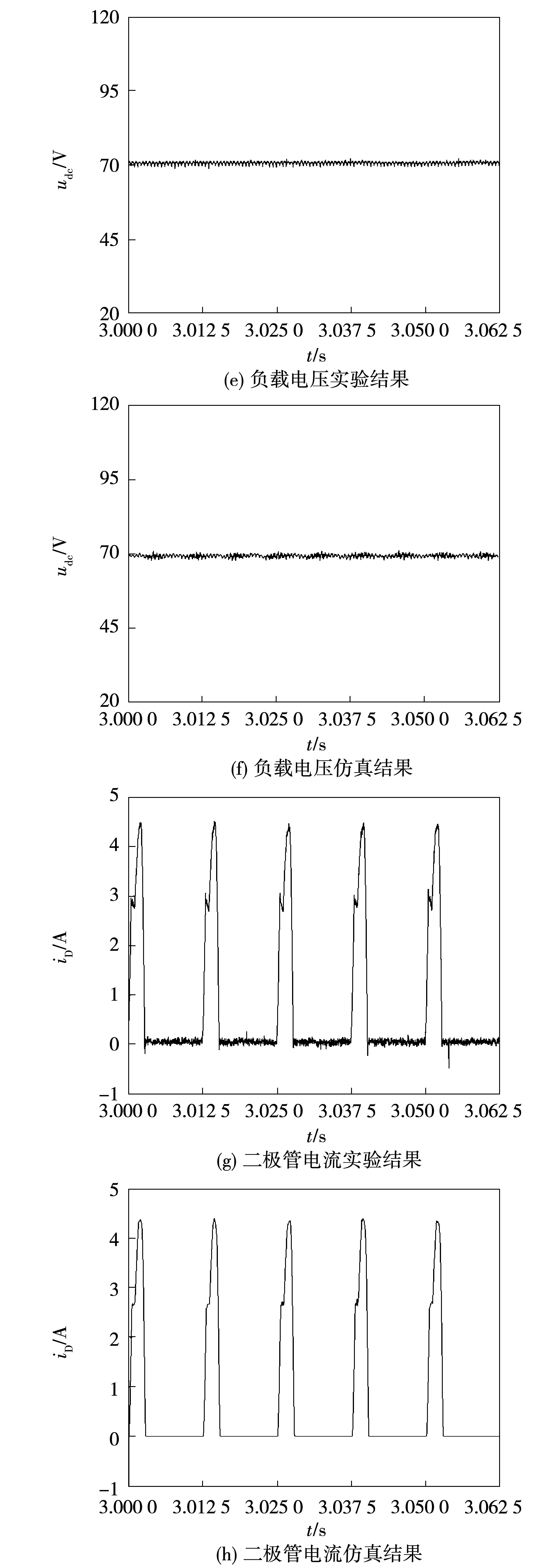
圖7 實驗和仿真的結果對比Fig.7 Experiment and simulation waveforms

4 運行特性分析與電氣量計算

4.1 實際工況下的仿真計算

基于某電廠11相環形無刷勵磁機及其整流系統的實際參數及運行條件進行實際工況的仿真計算，勵磁電壓設置為66 V(額定)，勵磁電源內電阻為0.48 Ω，勵磁機轉速為3 000 r/min，即電樞感應電勢基波頻率為250 Hz(周期為0.004 s)。通過仿真計算可得到電樞繞組相電壓，二極管電流，負載電壓以及負載側電流，如圖8所示。

圖8 11相無刷勵磁機實際運行條件下的仿真波形Fig.8 Simulation waveforms of 11-phase brushless exciter in actual operation conditions

不同于動模樣機的運行工況，實際運行時，電樞繞組的相電壓出現了一小段為0的時刻，而二極管電流也出現了更為明顯的雙峰波形。通過仿真中二極管的導通情況可以看到整流電路中同時導通6個或者7個二極管，這種情況下二極管導通過程對應的電角度為6π/22～7π/22。

4.2 實際工況下的等效電路

以二極管D9向D19換相狀態為例進行分析，如圖8(b)所示，此時電路中二極管D7、D9、D19、D0、D2和D12導通并進行換相，這個過程持續α1電角度。在下一個階段，二極管D7、D9、D17、D19、D0、D2和D12同時導通并進行換相，這個過程持續α2電角度。接下來，根據二極管導通順序繼續進行上述兩個階段的循環，即

α1+α2=π/11。

(16)

根據二極管導通情況可得第一、二階段等效電路圖如圖9所示。

圖9 等效電路圖Fig.9 Equivalent circuit diagram

在第一個階段，根據等效電路圖，可以得到電路支路方程為：

(17)

在第二個階段，根據等效電路圖，可以得到電路支路方程為：

(18)

在第一階段開始時，二極管D7、D9和D19的電流之和為Id，即

ID7+ID9+ID19=Id。

(19)

式中：ID7=ΔiD10(2)，ΔiD10(2)表示二極管D10電流在第二階段的變化量；ID9=-(ΔiD9(1)+ΔiD9(2))，ΔiD9(1)和ΔiD9(2)分別表示二極管D9電流在第一階段和第二階段的變化量；ID19=ΔiD10(2)+ΔiD7(1)+ΔiD7(2)，ΔiD7(1)和ΔiD7(2)分別表示二極管D7電流在第一階段和第二階段的變化量。

4.3 二極管電流的解析計算

在一個基波周期內，11相全橋整流電路會發生22次換相過程，因而交流側電樞繞組電壓可以分為22段，而且由于整流電路中導通6個或者7個二極管，在某些階段內電樞繞組兩端的電壓會保持為零，即滿足

(20)

針對實際運行狀況下的二極管電流波形，根據等面積原則可以將二極管電流的波形進行等值簡化，二極管電流的等值過程如圖10所示，而且同一橋臂相鄰波形始終相差2π/11電角度。

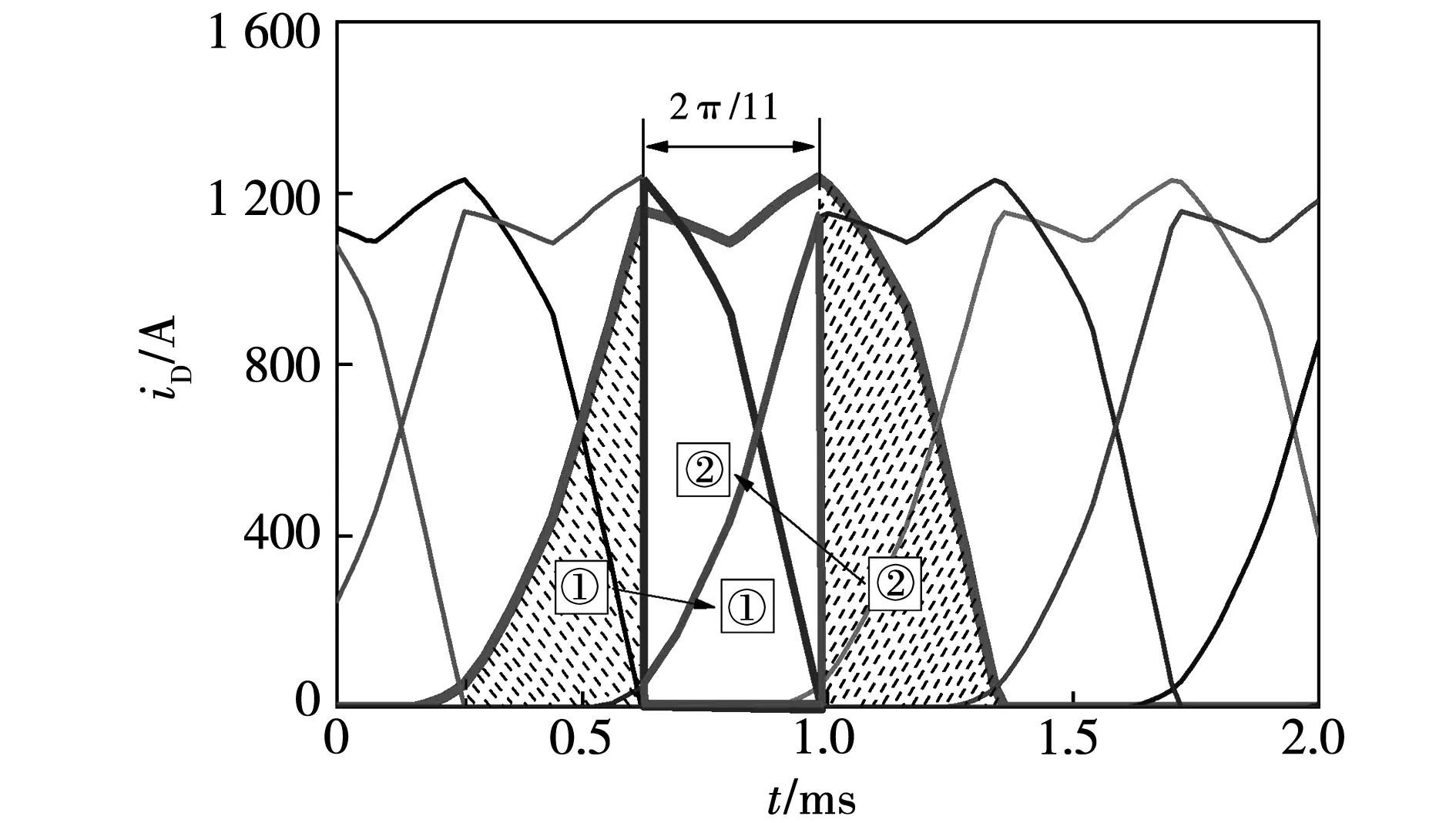
圖10 二極管電流的仿真波形Fig.10 Diode current simulation waveform

可以得到整流二極管電流的平均值表達式為

(21)

由仿真結果，負載側電流Id為2 420 A，整流二極管電流的平均值為226.7 A，根據式(21)計算的二極管電流平均值為220 A，說明式(21)的正確性。

4.4 負載側電壓的解析分析

正常運行時，整流電路中同時導通6個或者7個二極管，即圖9對應的兩個階段，對其進行等值化簡可得圖11所示的電路圖。

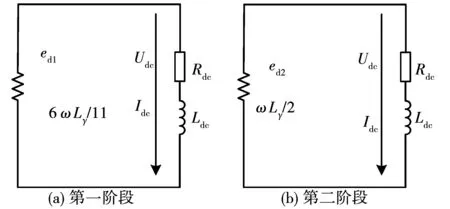
圖11 兩個階段的等值電路圖Fig.11 Equivalent circuit diagram at two stages

根據11相環形無刷勵磁系統等值電路的特點和式(1)進行電路等值化簡，可得圖11中兩個階段等值內電勢的表達式為：

(22)

(23)

電樞繞組內電勢的有效值為368 V，電樞感應電勢基波頻率為250 Hz(周期為0.004 s)，仿真計算得到的負載側電壓平均值為525.2 V，而通過式(22)和式(23)計算的負載側電壓為529.9 V，負載側電壓理論計算數值與仿真計算結果基本一致。

5 結 論

本文以11相環形無刷勵磁機及整流系統為研究對象，重點對其基本工作原理、數學模型以及運行特性進行了分析，基于動模實驗及仿真結果對11相環形無刷勵磁機的運行狀態進行了對比分析，并對實際工況下電氣量進行了解析計算，結論如下：

1)每次換相上下橋臂二極管之間應保持三相電樞繞組的串聯，二極管存在提前導通和多管同時導通現象，二極管電流不連續。

2)通過分析換相過程，得到了二極管平均電流與負載電流的關系，用解析方法推導出了等值內電勢的計算公式，得到了負載側電壓的平均值。

3)由于大容量無刷勵磁系統不具備實驗條件，本文在對動模樣機進行充分的分析和實驗并驗證方法的正確性后，可將結論延伸到實際電機上，大大提高經濟性和安全性。

本文可為11相環形無刷勵磁機及整流系統的優化設計提供依據，為分析多相整流系統的運行特性提供新思路。