基于改進PSO與廣義五階CKF算法的PMSM無傳感器控制

張榮蕓， 鄭常勝， 時培成， 趙林峰， 龔長富， 周成龍

(1.安徽工程大學 機械與汽車工程學院，安徽 蕪湖 241000；2.安徽工程大學 汽車新技術安徽省工程技術中心，安徽 蕪湖 241000； 3.合肥工業大學 汽車與交通工程學院，合肥 230009；4.安徽工程大學 高端裝備先進感知與智能控制教育部重點實驗室，安徽 蕪湖 241000)

0 引 言

永磁同步電機(permanent magnet synchronous motor，PMSM)因具有優良的控制性能而廣泛應用于汽車的自動化控制中。然而，其精確控制所需轉子轉速和位置信號一般由傳感器獲得。傳感器的使用使電機具有結構復雜、可靠性低、成本高和維護難等不足，限制了其應用范圍，降低了其系統魯棒性。因此，無傳感器控制技術成為了現代電機控制技術的一個重要研究方向。

隨著高性能數字信號處理技術的飛速發展，許多學者對PMSM轉速估計進行了廣泛研究。在零速或低速條件下，常用高頻注入法[1]對電機轉速進行估計，但該方法需基于電機的凸極效應，且在中高速運轉時存在高頻噪聲，估計精度較低。而在中高速條件下，常用基于模型的觀測器法來對電機轉速進行估計[2-3]。觀測器方法通過建立反電動勢或磁鏈觀測器，獲得轉子位置與轉速信息，但在模型搭建的過程中需要對電流信號進行微分，這會使噪聲信號放大，因此需要加入濾波環節，增加了算法的設計和調試工作。雖然，滑模觀測器法有良好的動態性能，但開關函數的存在帶來了系統抖振問題，影響了估計的精度。另外，還有擴展卡爾曼濾波(extended Kalman filter, EKF)算法[4-5]、無跡卡爾曼濾波(unscented Kalman filter,UKF)算法[6-7]和容積卡爾曼濾波(Cubature Kalman fitler,CKF)算法[8-9]。EKF算法具有較好的估計效果，但該方法通過對非線性系統進泰勒級數展開取第一項來對非線性系統線性化，存在高階截斷誤差，同時還需計算復雜的Jacobian矩陣，計算量大實現起來困難。UKF算法雖然不需要計算復雜的Jacobian矩陣，但由于在數值計算過程中存在舍入誤差，會引起協方差不對稱或非正定等不足，容易出現發散。CKF算法通過權值與容積點的計算，經過非線性方程的轉換后，產生新的容積點來給出下一時刻的狀態估計，不需要對系統進行線性化處理。可用于精確的電機轉速估計，但CKF算法是基于三階球面-相徑容積規則來近似高斯權值積分的，其估計精度只能達到三階。

另外，PMSM控制精度的提高，還可以通過改善其控制方法來實現。常見的PMSM控制方法是采用傳統的PI控制，其控制結構簡單，是當今工業控制中應用非常廣泛的控制算法。雖然PI控制有一系列優點，但傳統PI控制達到滿意控制效果所需的控制參數難以準確獲得。目前對PI參數進行優化的主要方法有：試湊法、專家規則法[10]、模糊控制[11]以及遺傳算法[12]等。其中，傳統的試湊法需要反復對PI參數進行調試，費時費力且誤差較大；專家規則法則與經驗知識相關，需要不斷整理和更新專家知識庫；模糊控制對于模糊規則和隸屬度函數的要求較高；遺傳算法較為復雜且易早熟收斂。因此，雖有較多方法用于PI參數的優化，但都存在一定的不足。

綜上所述，針對電機轉速估計精度及PI參數優化的問題，本文提出一種基于改進粒子群優化PI參數與廣義五階CKF的PMSM無傳感器控制方法。在推導出PMSM矢量控制中的電流環與速度環傳遞函數的基礎上，并以此為適應度函數，采用基于柯西變異的改進粒子群算法對速度環傳遞函數中的PI參數進行優化；推導廣義五階CKF算法，對PMSM轉速進行估計，實現基于改進粒子群優化PI參數和廣義五階CKF的PMSM無傳感器控制；最后，對本文提出的無傳感器控制算法進行電機臺架實驗，相比于CKF，廣義五階CKF對PMSM的轉速估計精度更高，且改進粒子群優化PI參數后的PMSM無傳感器控制效果較優化前也有明顯提高。

1 PMSM數學模型

根據表貼式永磁同步電機的電壓、磁鏈、電磁轉矩和機械運動方程，可得PMSM非線性數學模型在靜止坐標系下的狀態空間表示為：

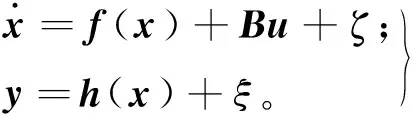
(1)

式(1)中的系數矩陣為：

其中：θ、ω為電機轉子位置和轉速；ψf、Rs、L分別是轉子永磁體磁鏈、定子電阻和電感。

根據Euler法，將PMSM的數學模型離散化可得：

(2)

設采樣時間為T，則式(2)中：

(3)

(4)

(5)

根據式(2)～式(5)，就可建立起PMSM的離散數學模型。

2 PMSM無傳感器控制

本文采用基于改進粒子群優化PI參數和廣義五階CKF算法來構建PMSM無傳感器控制。該控制策略采用id=0的矢量控制，為了改善控制效果，利用基于柯西變異的改進粒子群算法對轉速環中的PI參數進行優化；對于控制中所需要的轉子轉速和位置信號，利用所建立的PMSM數學模型，運用廣義五階CKF對其進行估計得到。本文對PMSM采用的無傳感器控制如圖1所示。

圖1 基于改進粒子群優化PI參數與廣義五階CKF的PMSM無傳感器控制系統Fig.1 PMSM sensorless control system based on the improved particle swarm optimization PI parameters and generalized fifth-order CKF

2.1 改進粒子群優化算法

粒子群算法(particle swarm optimization，PSO)屬于群智能算法，是一種進化計算技術，源于對鳥群捕食行為的研究。相比于其他智能優化算法，PSO具有迭代速度快、魯棒性好等優點。因此，本文采用PSO來對轉速環PI控制參數進行優化。

1)PSO算法。

首先在可行域中初始化一群粒子，每個粒子都代表極值優化問題的一個潛在最優解，用位置、速度和適應度三項指標表示該粒子的特征。粒子在解空間中的運動，可利用個體極值(Pbest)和群體極值(Gbest)更新個體的位置來進行描述。個體極值是指個體在所經歷位置中得到的適應度值最優位置，群體極值是指種群中的所有粒子搜索到的適應度最優位置。粒子每更新一次位置，就計算一次適應度值，如果其值比該粒子之前的適應度值都小，則更新適應度值、個體極值，且每次更新后，將所有粒子中對應的最小適應度值來更新群體極值。且在每次迭代過程中，粒子自身速度和位置是通過個體極值和群體極值來進行更新的[13]。

初始化時假設在D維搜索空間中有m個粒子,其第i個粒子的位置矢量為[14-15]

(6)

其速度矢量為

(7)

第i個粒子搜索到的最優位置為

(8)

整個粒子群搜索到的最優位置為

(9)

第i個粒子的位置和速度更新為：

(10)

其中：w為慣性因子，為非負數；c1，c2為加速常數，為非負數。r1，r2為介于[0，1]之間的概率值。

2)基于柯西變異的改進PSO算法。

為了增加傳統PSO算法種群的多樣性和避免陷入局部最優，本文將柯西變異算子引入到傳統PSO算法中，也即是當式(10)中的r1、r2為均小于或等于0.1時，就進行柯西變異，增加PSO種群以獲得全局最優[16]。

一維柯西分布的概率密度函數為

(11)

其中λ為大于0的系數，一維柯西分布的分布函數為

(12)

當λ=1時，式(12)為標準柯西分布。

引入柯西變異因子φ后，第i個粒子的位置和速度更新可表示為：

(13)

式中C(0,1)為標準柯西分布函數產生的隨機數。

為了提高柯西變異PSO的收斂速度和使其快速跳出局部最優，本文采用變化的柯西變異因子φ，當在PSO算法的早中期，采用較大的φ來跳出局部最優；當在PSO算法的后期，采用較小的φ來提高收斂速度。

因此，柯西變異因子φ可以表示為

φ=(G-n)/G。

(14)

式中：G為最大迭代次數；n為當前迭代次數。

之后，判斷更新后的粒子是否滿足迭代終止條件，若滿足則輸出最優解；若未達到終止條件，則從新計算適應度，并進行位置與速度更新。

柯西變異PSO算法的流程如圖2所示。

圖2 改進粒子群算法示意圖Fig.2 Diagram of the improved particle swarm optimization algorithm

為了對比分析PSO算法和基于柯西變異的改進PSO算法的收斂速度，以2.2節中PMSM轉速環傳遞函數為適應度函數，得到迭代次數與適應度函數值的關系曲線如圖3所示。

由圖3可以看出，相比于普通PSO算法，基于柯西變異的改進PSO算法在尋找目標函數的最優解時，能夠在更少的迭代次數下尋找到最優解。其中，普通PSO算法在330代左右得到最優解，而改進PSO算法在100左右就找到了最優解。另外，由圖中曲線走向可以看出，普通PSO算法在尋優時，會短時陷入局部最優(例如第20代到第32代)，而改進PSO算法則可以有效避免這種情況出現。因此，基于柯西變異的改進PSO算法相比于普通PSO算法具有更快的迭代速度和更好的全局搜索能力。

圖3 PSO算法與改進PSO算法的迭代速度對比曲線Fig.3 Iterative speed comparison curves of the PSO algorithm and improved PSO algorithm

2.2 PMSM轉速環傳遞函數

對PMSM進行控制，常采用PMSM磁場定向雙閉環控制策略，它是一種含有電流環和轉速環的雙閉環系統。本文以該雙閉環系統的轉速環傳遞函數來作為PSO算法的適應度函數。

根據文獻[17]，工程設計PMSM雙閉環控制的原則是先內環后外環，設計步驟是：先從電流環開始，對其進行必要的變換和近似處理后，對電流環進行校正(一般校正成2階系統)，最后按動態性能指標要求來確定電流調節器的參數。電流環設計完成之后，把電流環等效成轉速環中的一個環節，再用同樣的方法設計轉速環，一般將其校正為3階系統。因電流環的控制對象為PWM逆變器和電機電樞回路，且電機的傳遞函數一般不隨外部負載變化，具有穩定的結構，故令PI調節器中的Kic=Kpcτc，可得到電流環的開環傳遞函數為

(15)

其中：Kpc為電流環PI調節器比例系數；KPWM為逆變器的放大倍數；TPWM為PWM逆變器的開關周期；Lq和Rs分別為電機電感和電阻。

再令τc=Lq/Rs，可以將式(15)轉化為二階系統的電流環閉環傳遞函數

(16)

在設計轉速環時，可以將電流環的傳遞函數看作是簡單的一階環節。根據上式電流環閉環傳遞函數和轉速環具有較低截止頻率的特點，可以將電流環閉環傳遞函數去掉高次項進行降階近似為

(17)

(18)

經過以上步驟即可得到PMSM的轉速環傳遞函數，以此為適應度函數，接著利用改進粒子群算法對轉速環PI參數進行優化，即可得基于改進粒子群PI參數優化的PMSM控制系統。

2.3 廣義五階CKF算法

目前，CKF對高斯濾波中的高斯積分采用三階球面-相徑容積規則來進行近似求解，可以達到三階估計精度。本文為提高PMSM轉速的估計精度，運用廣義五階容積規則來對高斯積分進行求解。對于離散系統，將貝葉斯估計基本理論與廣義五階容積規則相結合，即可推導出廣義五階CKF濾波方法。

廣義五階容積積分公式如下[18-20]

n≥2。

(19)

(20)

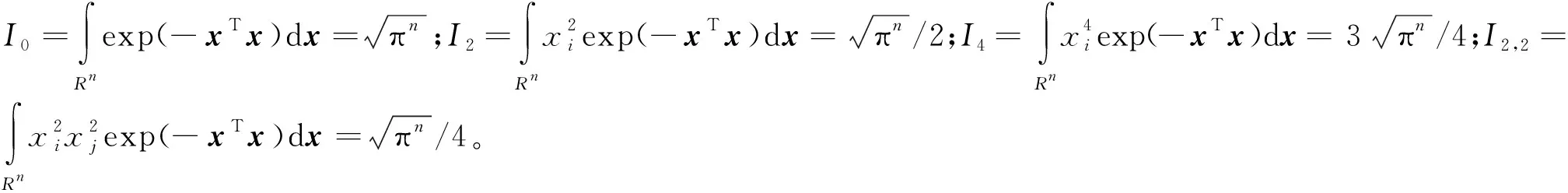
由此可得式(20)的唯一解為：

將式(19)轉化成標準高斯分布的形式，可得

(21)

可得到容積點集和相關權重如下：

1)時間更新。

①計算容積點xk,i(i=0,1,…,2n2+1)：

(22)

②計算通過狀態方程傳遞后的容積點xk+1/k,i：

xk+1/k,i=f(xk,i)。

(23)

③計算k+1時刻的狀態預測值：

(24)

④估計k+1時刻的狀態誤差協方差矩陣Pk+1/k：

(25)

2)量測更新。

①計算更新后的狀態容積點xk+1/k,i：

(26)

其中，Sk+1/k為Pk+1/k經過Cholesky得到的矩陣，i=1,2，…,2n2+1。

②計算通過測量方程傳遞的容積點yk+1,i：

yk+1,i=h(xk+1/k,i)。

(27)

(28)

(29)

⑤計算k+1時刻的濾波增益矩陣Kk+1：

(30)

(31)

⑦估計k+1時刻的狀態誤差協方差陣Pk+1：

(32)

給定初始值，就可以經過上述流程進行廣義五階CKF估計，其流程圖如圖4所示。

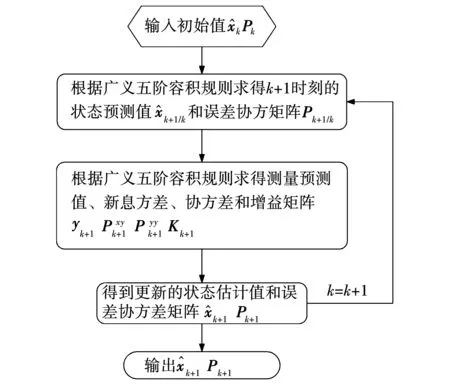
圖4 廣義五階CKF的流程圖Fig.4 Flow chart of the generalized fifth-order CKF

3 實驗驗證

為驗證所提PMSM無傳感器控制方法的實際控制效果，搭建了如圖5所示的電機實驗臺架，實驗臺主要由上位機、電機驅動實驗箱和永磁同步電機組成。在上位機MATLAB/Simulink環境中打開并生成基于CKF和廣義五階CKF算法的PMSM無傳感器控制模型代碼，通過CCS6.2編譯后生成可以在DSP中運行的C代碼，再通過連接上位機與實驗臺的仿真器將代碼下載到電機實驗箱中的TMS320F28335DSP之中，電機控制箱通過控制逆變器輸出驅動信號，控制PMSM工作。上位機可以通過串口工具來接收實驗數據，進行參數在線調節，控制PMSM的轉速。

圖5 電機實驗臺架Fig.5 Motor test platform

實驗時工況為電機轉速由800 r/min階躍到1 000 r/min的轉速突變工況，實驗結果如圖6～圖11所示。

圖6 轉速估計曲線Fig.6 Speed estimation curve of experiment

圖6和圖7為實驗時分別采用CKF與廣義五階CKF算法進行PMSM轉速估計及其估計誤差的對比曲線。由圖可知，在轉速階躍時，廣義五階CKF算法可以穩定的估計出電機的轉速。當電機的轉速由800 r/min階躍至1 000 r/min時，轉速估計誤差會增大一些，但很快穩定下來，并且整個過程中廣義五階CKF算法的估計誤差都較小。因此，實驗驗證了廣義五階CKF算法在轉速突變時，相較于CKF算法，其估算精度更高，對轉速突變具有較好的適應性。

圖7 實驗轉速估計誤差曲線Fig.7 Speed estimation error curve of experiment

圖8和圖9為實驗時分別采用CKF與廣義五階CKF算法進行PMSM位置估計及其估計誤差的對比曲線。由圖可知，實驗中廣義五階CKF算法可以準確的估計出電機的轉子位置，并且在轉速突變過程中，其估計精度都要比CKF算法高。表1為轉子轉速和位置誤差的方差對比，反映了轉速和位置誤差與零的偏離程度，從表中可以看出廣義五階CKF的方差都要比CKF的小，說明其估計的精度比CKF要高。因此，實驗結果進一步驗證了本文所提的利用廣義五階CKF算法來對PMSM的轉子位置進估計的方法，有更高的估計精度。

圖8 實驗轉子位置估計曲線Fig.8 Rotor position estimation curve of experiment

圖9 實驗轉子位置估計誤差Fig.9 Rotor position estimation error curve of experiment

表1 轉子轉速與位置誤差的方差對比

圖10和圖11分別表示實驗時轉速環PI參數分別采用基于柯西變異的改進粒子群、普通粒子群和無粒子群優化且均采用廣義五階CKF算法來對PMSM轉速和轉子位置進行估計的誤差對比曲線。由上圖可以看出，相較于普通粒子群算法，基于柯西變異的改進粒子群算法優化的廣義五階CKF算法在實驗中轉速和位置估計的誤差都要比普通粒子群算和無粒子群算法的要小。并且在轉速突變時，本文提出的基于改進粒子群優化的廣義五階CKF算法依然能夠進行精確的估計，具有較小的誤差。表2表示在實驗時，轉速環PI參數采用3種算法優化的廣義五階CKF算法的轉速和轉子位置誤差的方差，從表中數值能夠說明基于柯西變異的粒子群優化的廣義五階CKF算法的方差要小于另外兩種方法，說明其能夠提高PMSM轉速的控制精度。因此，實驗結果說明對PMSM轉速環PI參數利用基于柯西變異的改進粒子群算法進行優化，是能夠明顯提高PMSM轉速控制精度的。

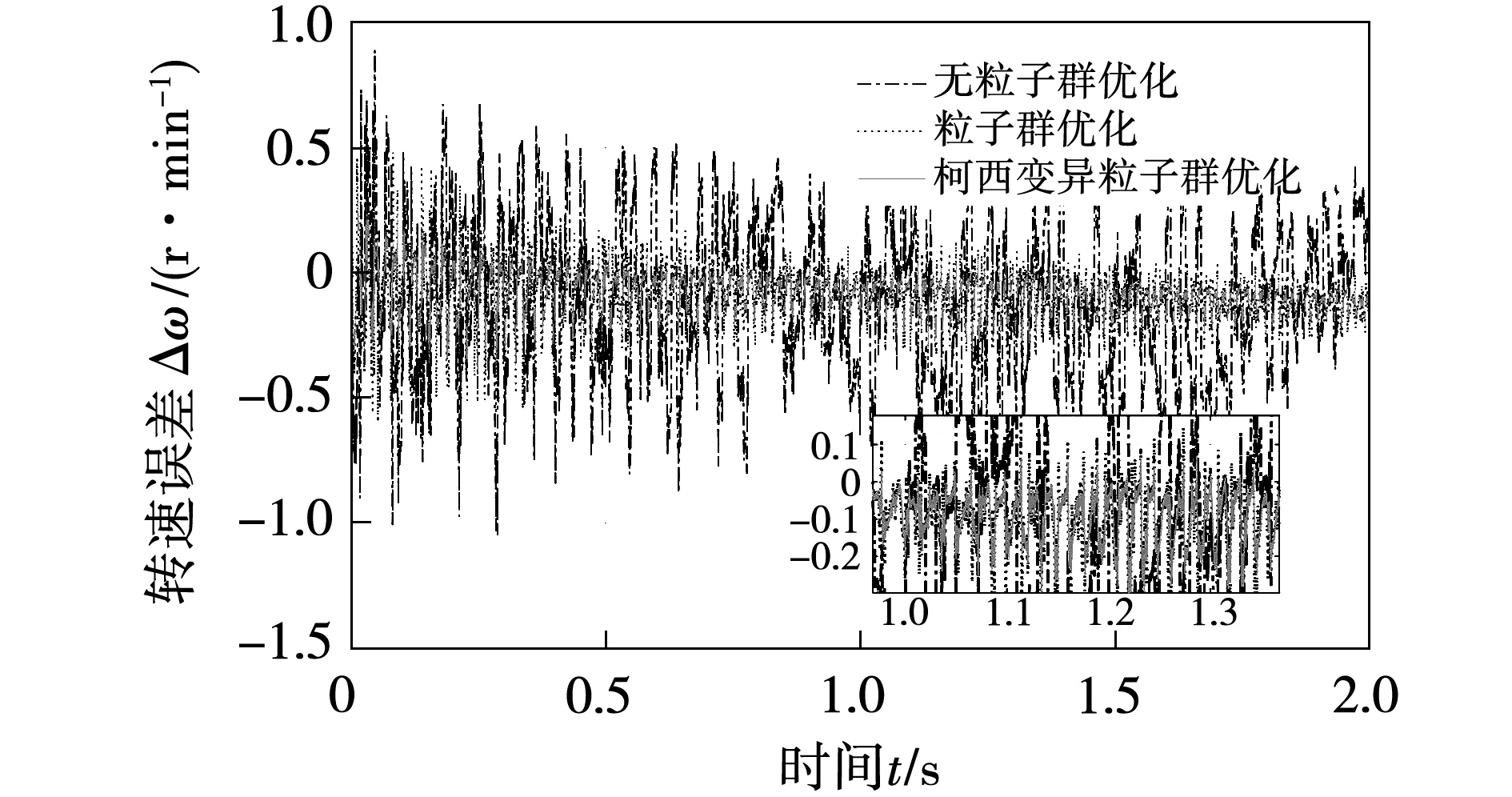
圖10 實驗3種優化方法下轉速估計誤差對比曲線Fig.10 Comparison curves of the speed estimationerror of experiment under three optimization methods

圖11 實驗3種優化方法下轉子位置誤差對比曲線Fig.11 Comparison curves of the rotor position estimation error of experiment under three optimization methods

表2 3種優化方法下轉子轉速與位置誤差的方差對比

4 結 論

為了提高PMSM無傳感器控制效果，本文主要利用所推導的轉速環傳遞函數為適應度函數，利用基于柯西變異的改進粒子群算法對PMSM轉速環的PI控制參數進行了優化；并利用廣義五階容積規則推導出了廣義五階CKF算法，最后構建了基于改進粒子群算法優化PI參數和廣義五階CKF的PMSM無傳感器控制方法，并進行了電機的臺架實驗。結果表明，廣義五階CKF算法比傳統的CKF算法在對PMSM進行轉速和位置估計時，具有更加良好的估計精度，并且通過對轉速環PI參數優化前后的基于廣義五階CKF算法對PMSM轉速和位置進行誤差對比實驗分析中，可知通過對轉速環PI參數的優化能夠有效提高PMSM的控制效果。

該算法不僅可以應用在車用永磁同步電機的控制中，對于工業領域內其他行業的電機控制也可以應用。接下來將對該算法實時性的進一步提高進行研究。