考慮摩擦時剛性直桿傾倒的運動分析1)
李浩隆 馮維明
(山東大學土建與水利學院,濟南250061)
經典力學中常見關于剛性直桿自由傾倒的問題(圖1),可利用動量定理、動量矩定理和動能定理來分析桿件在傾倒過程的運動。但教材中此問題多見于理想狀態下(考慮地面為光滑的)運動學分析和動力學分析[1-2]。如果考慮一般情況下即地面有摩擦時剛性直桿傾倒過程,問題立刻就復雜了許多,2017年《力學與實踐》曾就此問題公開征集解答[3],這也引起了許多任課教師和在校學生的興趣,近年來不少學者對此問題展開討論,表達了自己的見解。在早期的文獻中,王曉云[4]計算了剛性桿完全倒地的時間,假設桿始終做定軸轉動,把桿觸地端理想地看作鉸鏈;2000年,高桂林等[5]討論了剛性桿在有摩擦的水平面上傾倒過程的力學分析,文章注意到了摩擦力在桿件傾倒過程會改變方向,研究了在特定摩擦因數下桿件觸地端約束力分析和運動分析,但缺乏一般情形下的相關分析,所以對可能出現的一些現象沒有進一步解釋;2018年,唐有綺等[6]再一次對剛性直桿傾倒過程進行了動態分析,通過數值解分析了直桿角位移、角速度、觸地端摩擦力等隨時間變化的規律,雖比前者分析更深入,但仍然欠缺全面分析,且其桿件觸地端摩擦力“始終向右”和摩擦力較大時桿件傾倒過程一直做定軸轉動的結論都是不正確的;同一時間,蘇振超等[7]研究了直桿傾倒時開始打滑的打滑角與摩擦因數的關系,通過對一道習題的分析,設計了已知打滑角求摩擦因數和已知摩擦因數求打滑角正反兩個問題,并得出了摩擦因數與打滑角關系的曲線圖,但圖中有一段曲線無意義,沒有得到打滑角與摩擦因數的完整關系,對桿觸地端滑動后的運動方向的判斷缺乏完整性;同年胡開鑫等[8]就此問題給出了兩點結論,均質桿傾倒過程中觸地端不會脫離地面且可在兩相反方向滑動,否定了文獻[6]的結論,并為此給出簡單的證明,但其桿觸地端左右滑動的判定條件值得商榷。2019年,張九鑄[9]討論了均質直桿無滑動傾倒時觸地端脫離水平面的條件,認為在某一角度“一定能實現無滑動脫離水平面”,該文的結論與文獻[5,8]是矛盾的。綜上所述,此前的研究主要是建立動力學方程并進行數值求解,沒有求得解析解,對于摩擦因數與打滑角關系的認識不夠深入,對不同摩擦因數下桿運動的求解不夠完整,甚至有些錯誤的結論。本文將盡可能對均質直桿傾倒過程進行完整的分析,對各種可能出現的現象進行分析,并對某些結論進行具有可信度的驗證,彌補以往研究中的缺陷,提出對前期研究不同的思考以供大家討論。
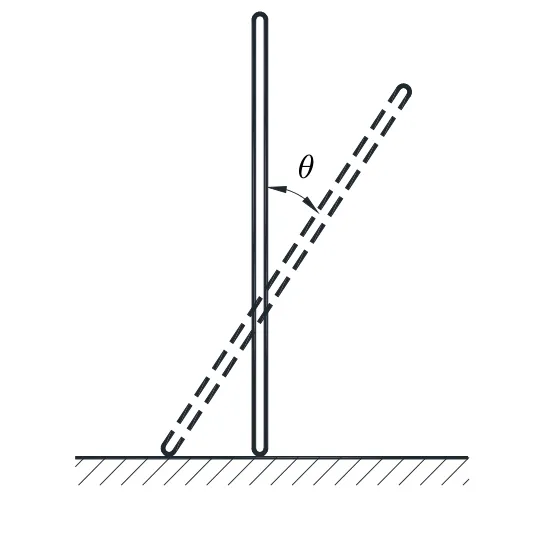
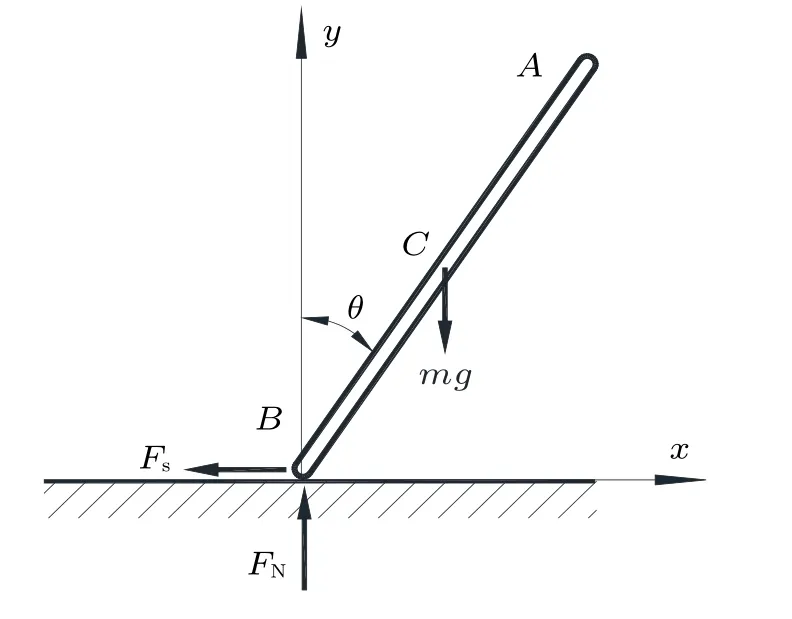
圖1 直桿傾倒示意圖
1 動力學建模與分析
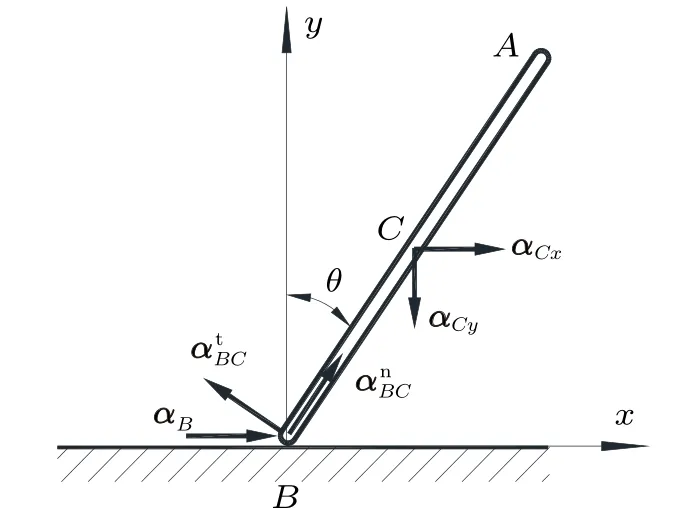
一質量為m,長為l的均質直桿豎直立在地面上,桿與地面的摩擦因數為f,隨后受到微擾開始自由傾倒,如圖2,剛開始運動時θ較小,桿先做定軸轉動,隨后桿觸地端開始打滑,設打滑角度為θ1,之后桿做平面運動,那么自然有這樣的問題:打滑角θ1如何確定?桿做平面運動狀態是怎樣的?如何求解桿觸地端的位移?
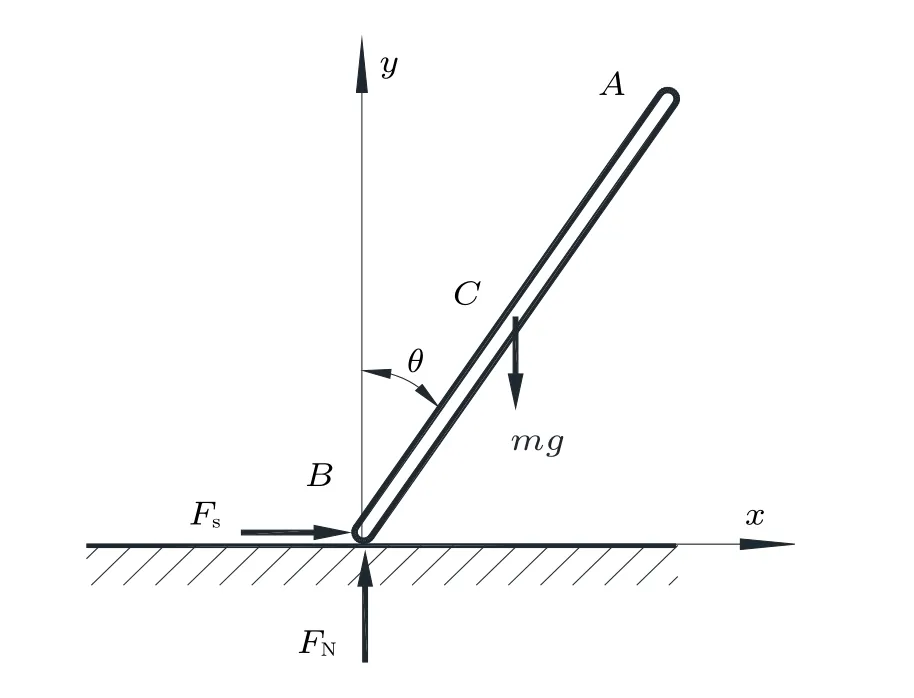
圖2 桿做定軸轉動時的受力分析圖
1.1 定軸轉動過程
設桿角速度為ω,由動能定理

得
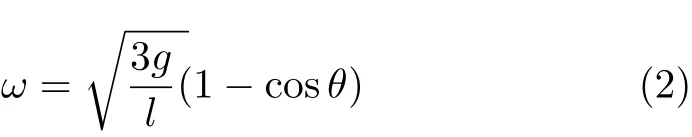
則質心C的水平速度為
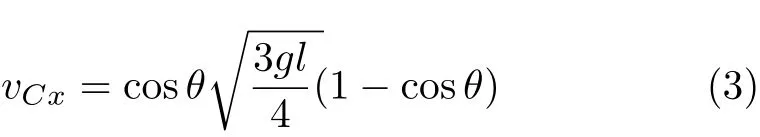
式(2)再次對t求導得
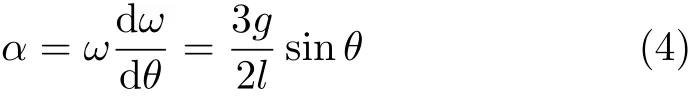
設a Cx和a Cy為桿質心C的加速度沿x和y軸的分量,如圖3,由質心運動定理
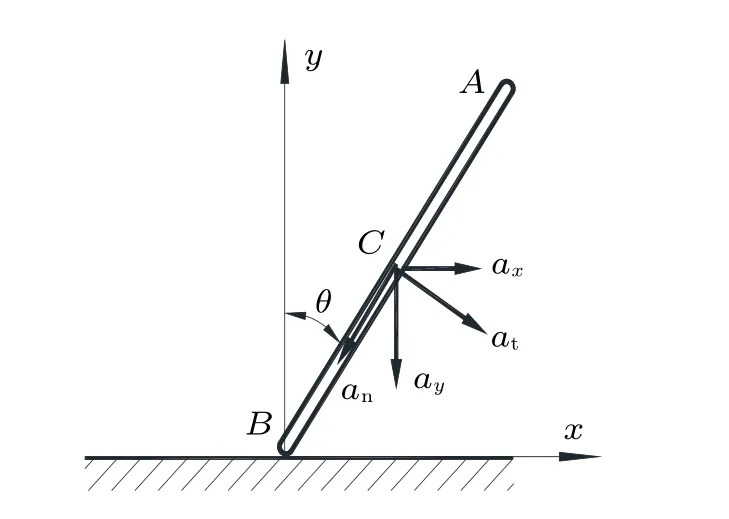
圖3 桿做定軸轉動時質心加速度的兩種分解圖
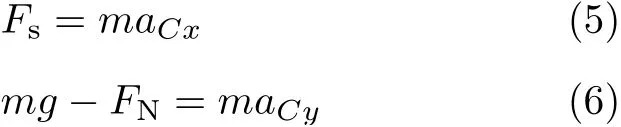
將a Cx和a Cy用切向加速度at和法向加速度an分別表示
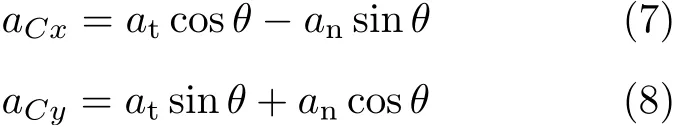
又at=αl/2,an=ω2/2。
同時將式(7)、式(8)分別代入式(5)、式(6)求得
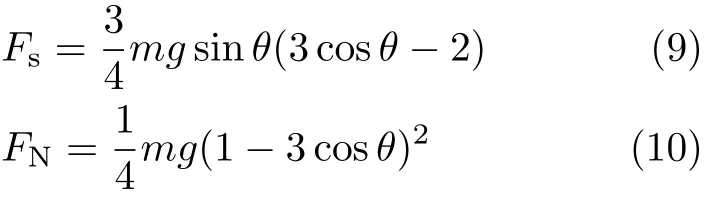
顯然FN≥0,當且僅當θ=arccos1/3≈70.5°時取等號,故桿在定軸轉動時不會跳起。對于Fs,在定軸轉動過程中,當θ≤2arccos1/3≈48.2°時,Fs≥0,也就是摩擦力向x軸正向,此時桿觸地端不打滑所要求的最小f滿足Fs=f FN;當θ≥48.2°時,Fs≤0,也就是摩擦力向x軸負向,此時最小f應滿足Fs=?f FN,故統一地有
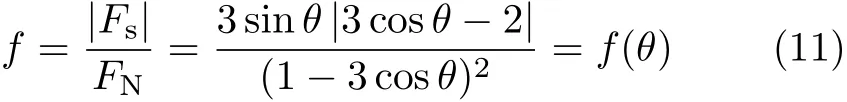
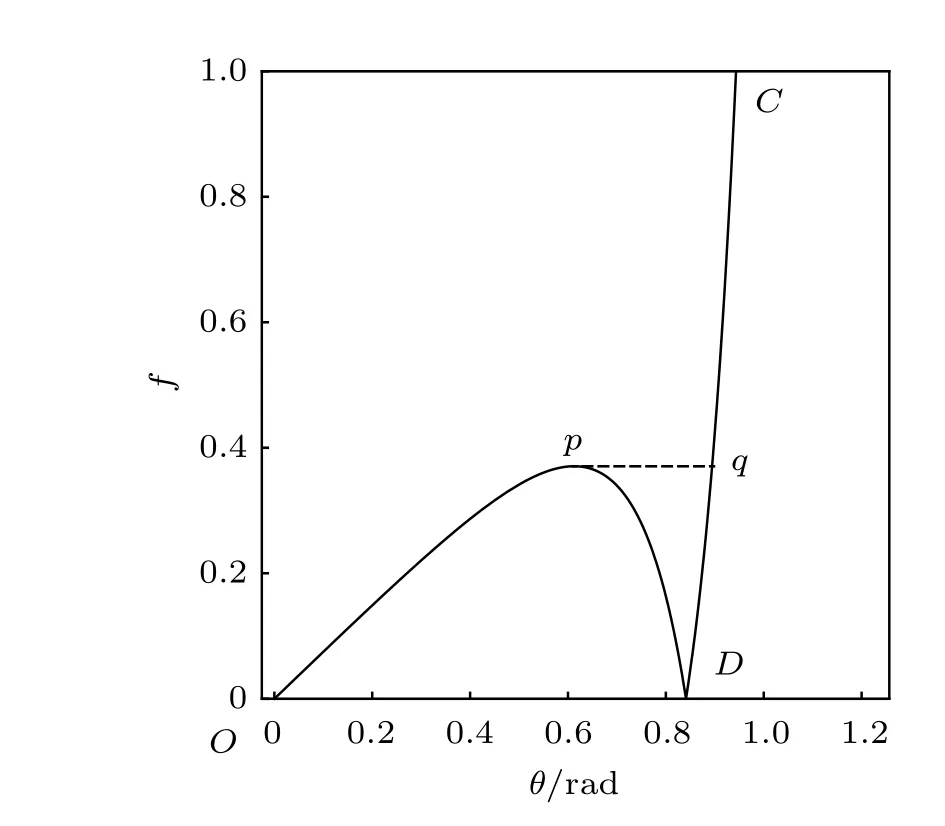
圖4 f關于θ的函數曲線圖
由f′(θ)=0,得,代入式(11)可得曲線極大值
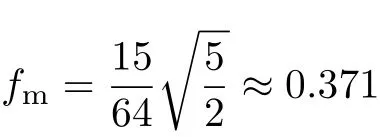
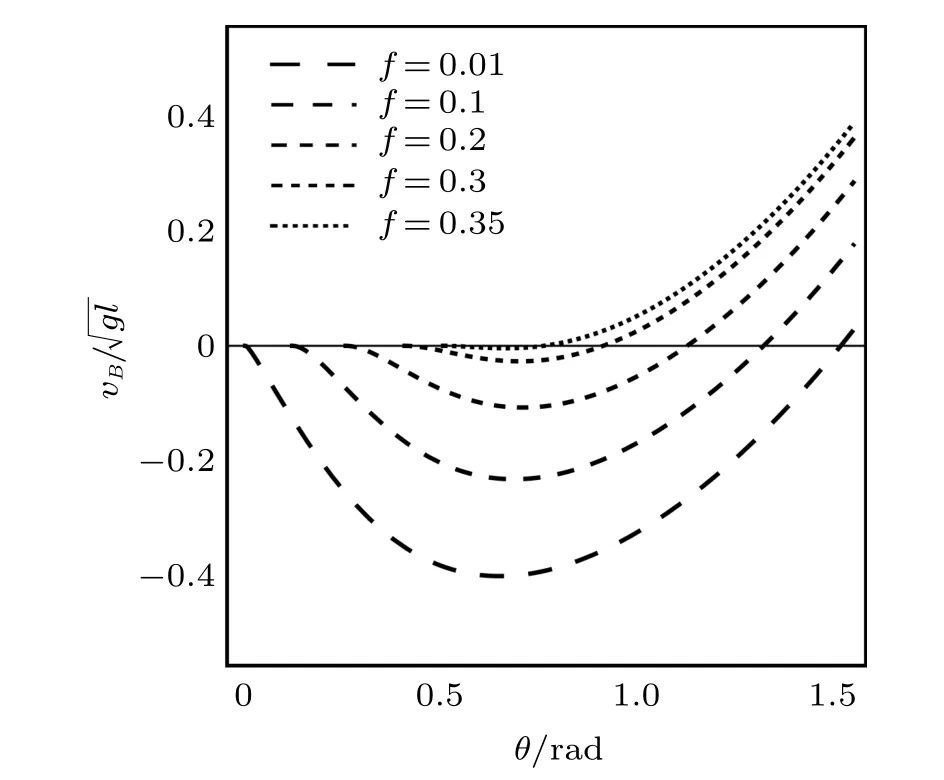
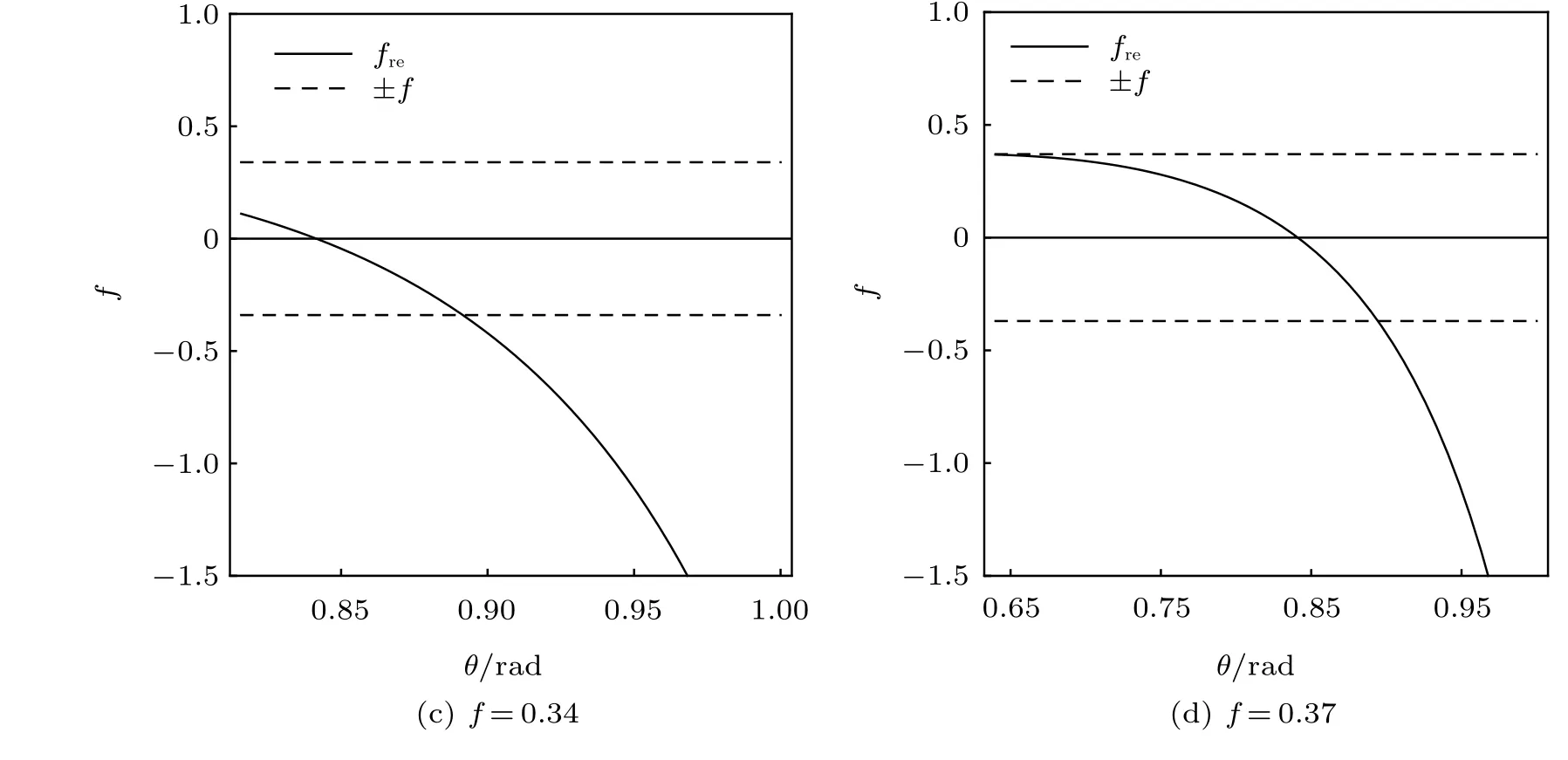
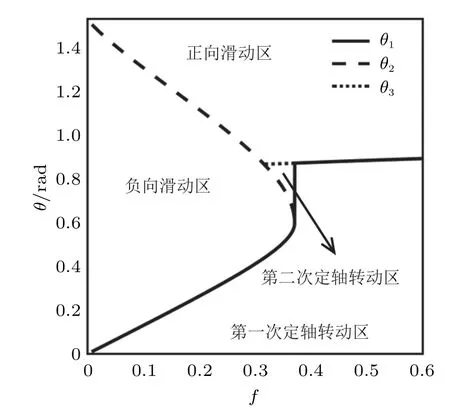
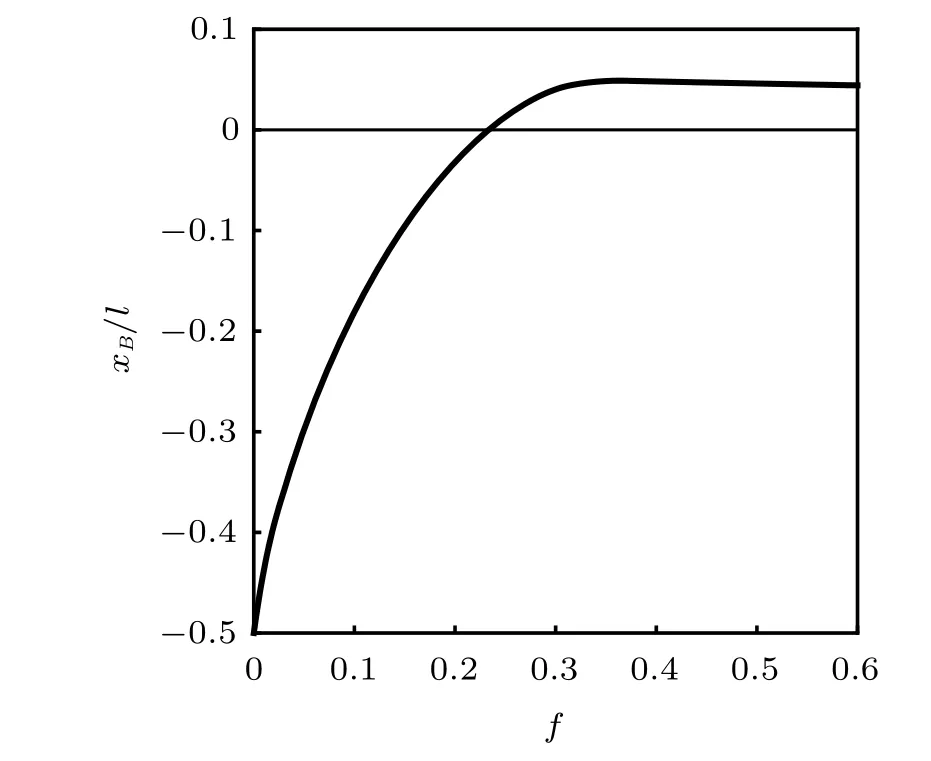
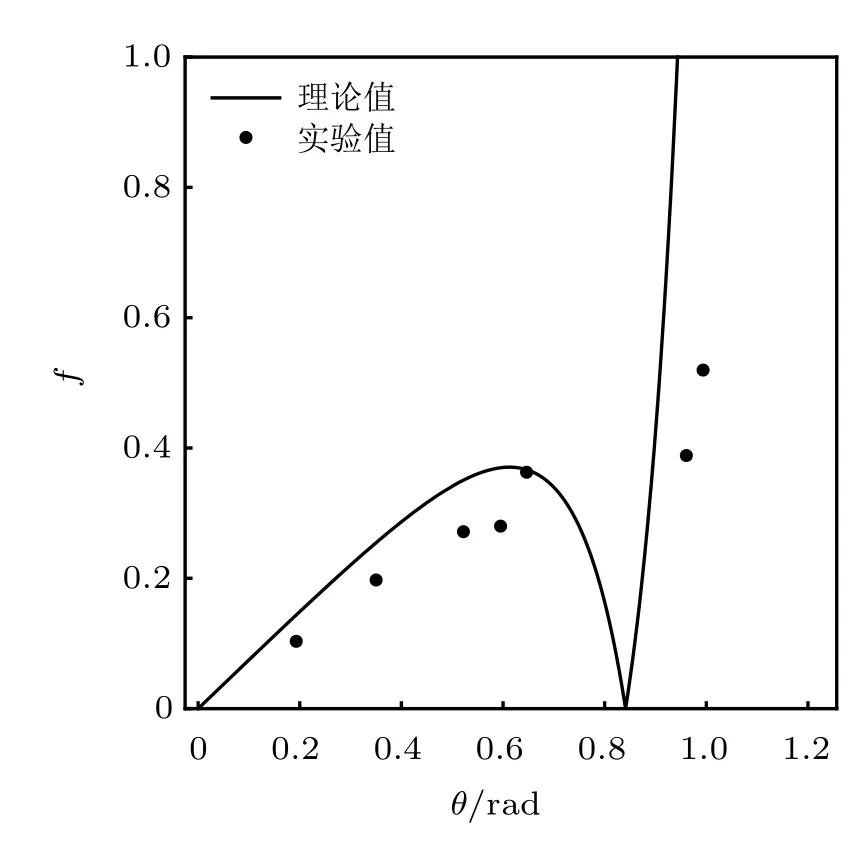
設此極值點為p,過p做平行于x軸的線交曲線于點q,q點橫坐標為0.894,約等于51.2°。需要注意,圖4是在定軸轉動的情形(即式(11))下畫出的,一旦觸地端開始滑動,桿就進入平面運動狀態,動力學方程將在后文給出。在f 由上面討論可知,直桿傾倒過程中首先發生定軸轉動(除f=0外),其次是平面運動,桿件觸地端運動過程以摩擦因數fm為界而不同。因此,需分別討論。 1.2.1f 此時桿打滑的θ1滿足 由剛體質心平面運動微分方程 由滑動摩擦(見圖2) 聯立式(13)和式(14)可得 如圖5,以C為基點,B為動點,B點加速度表示為 圖5 桿做平面運動時的加速度分析圖 向y軸正向投影得 聯立式(15)和式(17),注意到α=d2θ/dt2,ω=dθ/dt,可以得到關于θ(t)的二階非線性非齊次微分方程 式(18)沒有解析解,利用變換d2θ/dt2=ωdω/dθ,并定義無量綱角速度化簡得 進一步整理得 它為n=?1的Bernoulli微分方程[10],其中 所以方程通解為 對于f=0的情況,式(20)可以積出 但f0時,無法全部積出。 在初步的分析中,往往認為觸地端的運動是單向的,但實際上不然。 以C為基點,B為動點,則B點速度為 質心任意時刻的水平速度表示為 其中a Cx為質心水平加速度式(15),v Cx0為觸地端開始滑動時質心的速度,由式(3)知 將式(23)代入式(22),整理可得 圖6 不同摩擦因數下v B/隨θ變化的曲線 當觸地端速度為零時,桿要么定軸轉動,要么轉而正向滑動,可以先判斷桿能否定軸轉動。 設桿從θ=θ2開始定軸轉動,此時桿角速度為ω2。 由動能定理 得 加速度仍為式(4),由式(5)~式(8)得 將式(4)、式(27)代入式(28)、式(29)得無量綱力 取f為0.31,0.32,0.34,0.37,如圖7,虛線代表±f,實線代表fre,隨著桿的傾倒,角度不斷增大,桿定軸轉動所需的最小摩擦因數也在變化,fre為正代表摩擦力也是正向,注意到f大于一定值時,實線有一段落在虛線范圍內,桿可以定軸轉動,后數值求解得到此值約為0.317。當實線與虛線相交時,桿開始打滑,設為θ3,由圖可知當f∈(0.317,0.370),打滑時fre<0,則摩擦力方向為x軸負向,桿只能正向打滑。 圖7 不同摩擦因數下桿所需的最小摩擦因數圖(續) 式(11)中以θ為自變量,但實際上桿的運動特性由摩擦因數f決定,結合對圖4的討論,把f作為自變量,并略去沒有物理意義的多解分支,數值求解得到桿第一次打滑角θ1與f的關系,通過數值求解式(25)的零點,得到桿觸地端減速為零時桿的傾斜角θ2,通過求解|fre|=f,得到第二次桿定軸轉動的打滑角θ3,將θ1,θ2和θ3畫在一個圖里,如圖8。 圖8 θ1,θ2,θ3與f的關系曲線 f軸可以分成三段:(0,0.317)、(0.317,0.370)、(0.370,+∞),分別對應三種情況。第一段內,桿從豎直開始傾倒,先定軸轉動,然后觸地端打滑開始負向運動,減速為0后開始正向運動,直至落地;第二段內,桿從豎直開始傾倒,先定軸轉動,然后觸地端打滑開始負向運動,減速為0后開始定軸轉動,之后打滑開始正向滑動直至落地;第三段內,桿從豎直開始傾倒,先定軸轉動,然后觸地端打滑開始正向運動,直至落地。 當桿正向滑動后(圖9),摩擦力反向,需將式(14)改為Fs=?f FN,可以看做是將摩擦因數變為相反數,故運動方程應為 圖9 桿正向滑動時的受力分析 當f∈(0,0.317)時,此方程初值由式(19)得到,當f∈(0.317,0.370)時,方程初值由式(27)得到。 1.2.2f>fm時的桿件平面運動 此時桿打滑的θ1滿足 運動方程同式(33),通解同式(20),其中 代入初值條件,求得 還要指出對任意的摩擦因數桿均不能跳起。設桿定軸轉動最后一刻的動能為E0,此后桿將發生平面運動,觸地端將會向x軸正向滑動,角速度和角度的關系難以精確求出,故利用放縮的辦法,假設此時桿繼續定軸轉動,此后角速度為ω1,由動能定理可知 其中WG為桿轉到θ時重力做的功。 但實際上,桿為平面運動,角速度為ω2,質心速度大小為v2,由動能定理可知 其中Wf為摩擦力做功的大小,利用速度疊加求得 式(36)減去式(37)得 由于式(12)右端大于零,則 而ω1是定軸轉動的角速度,可見打滑時的角速度比定軸轉動時的更小,利用式(13)和式(17)與補充條件Fs=?f FN,求得無量綱反力 放縮得 代入式(2)得 這樣,證明了支反力恒正。其他摩擦因數下的證明思路一致,這里不再贅述。 當f 當θ1<θ<θ2時,利用式(22)知負向位移為 其中t1為桿觸地端開始滑動的時刻,t2為停止滑動(或開始反向滑動)的時刻 將式(23)代入式(42),經部分積分后可得 其中第三項利用換元法把積分變量換為θ 由于位移與桿的長度有關,式(42)兩端同除桿長l,得到無量綱位移x B1/l 同理可推得,當θi<θ<π/2時,無量綱正向位移為 當f∈(0,0.317)時,θi取θ2,當f∈(0.317,0.370)時,θi取θ3,故觸地端總位移x B/l=x B1/l+x B2/l。 當f≥fm時,觸地端只有正向位移,同樣可導出觸地端位移表達式為 得到觸地端最終位移與摩擦因數的關系曲線,如圖10。 圖10 x B/l與f的關系曲線 圖10中的曲線在f=0.233附近有零點,也就是此時觸地端會回到初始位置,曲線在f=0.364附近有極大值點,極大值約為0.049,此時觸地端離初始位置最遠。 考慮到滑動摩擦因數測試較為困難,本實驗主要通過測得靜摩擦因數后,測試從定軸轉動到初始滑動的臨界角度,即圖4中所示初始滑動臨界曲線。同時驗證對應不同摩擦因數桿觸地端的運動狀態。首先需要取不同的介質獲得不同的摩擦因數,然后對應在不同介質表面進行直桿傾倒實驗。 實驗選用均質的細長不銹鋼桿,長300 mm,直徑2 mm,兩端打磨成弧形,并均勻地裹上一層硬脂酸,以保證在滑動過程中摩擦因數的均勻性。 靜摩擦因數的直接測量較難,可以通過圖11的方法進行間接測量:將桿靠在直角墻面上,設桿與鉛錘方向夾角為θ,釋放后,如果桿打滑,就減小角度再重新擺放,如果不打滑則小心增大角度再重新擺放,精細調整至臨界狀態。 圖11 桿受力分析圖 設A和B段支反力和摩擦力分別為FNA,FSA,FNB,FSB,摩擦因數分別為f A和f B,當桿達到臨界平衡時,由平衡方程得 由于上、下端均達到最大靜摩擦力,則補充方程為 式(49)和式(50)共五個方程,卻有六個未知量,故可以認為一端摩擦因數已知,來測量另一端摩擦因數,如f B已知,可求得 B端的摩擦因數可以這樣求得,將水平面與垂直面用同一種材質,此時A和B端摩擦因數相同,可設為f,從式(51)可解出 選定水平面和垂直面材質均為A4紙,測得臨界角為39°,則f B=f=0.354。下面的實驗中,垂直面的材質保持不變(A4紙),更換水平面的材質重復上述實驗過程獲得相應的臨界角,通過式(39)確定A處相應的摩擦因數,所得結果如表1所示。 表1 不同材料下的摩擦因數 為了控制直桿倒下的方向,直桿的頂部靠在一根光滑的細鋼桿上,直桿后面有角度表,用高速攝像錄制直桿傾倒的過程,通過回放可以讀出桿觸地端滑動時的臨界角,準備就緒的裝置如圖12。 圖12 傾倒裝置示意圖 實驗得到的不同摩擦因數下初次滑動臨界角如圖13所示,圖中曲線為理論值(見圖4),各點為實驗值。整體趨勢較為符合理論解。這里必須正視兩個偏差:(1)靜摩擦因數是在盡可能保持桿件不受其他因素影響下(如保持絕對靜止)測得的最大靜摩擦因數。但桿件傾倒過程測試時,從定軸轉動到觸地端開始滑動前難以符合靜摩擦因數的測試環境,因此實際摩擦因數降低了(介于靜、動摩擦因數之間);(2)慢鏡頭實際觀察滑動臨界角時仍有延遲,測量結果整體偏大(即圖中各點偏右)。 圖13 實驗值與理論曲線對比圖 圖14為摩擦因數f=0.29時桿的運動狀態。圖14(a)為初始位置,桿觸地端在刻度5的位置;圖14(b)為定軸轉動過程,桿觸地端仍在刻度5的位置;圖14(c)為桿觸地端反向滑動過程中,桿觸地端位于刻度5的左邊;圖14(d)為桿觸地端正向滑動過程中,桿觸地端位于刻度5的右邊,定性驗證了當f<0.317時,桿傾倒過程的運動分析。 圖14 f=0.29時,直桿傾倒過程截圖 圖15為摩擦因數f=0.519時桿的運動狀態。圖15(a)為初始位置,桿觸地端在刻度5的位置;圖15(b)為定軸轉動過程,桿觸地端仍在刻度5的位置;圖15(c)為桿觸地端正向滑動過程中,桿觸地端位于刻度5的右邊;桿傾倒過程中無反向滑動。定性驗證了當f>fm(0.370)時,桿傾倒過程的運動分析。 圖15 f=0.519時,直桿傾倒過程截圖 f∈(0.317,0.370)時,桿雖然存在第二次定軸轉動,但時間極短,并且前述分析并未考慮動靜摩擦因數的不同,在實際實驗時,難以準確地觀測到第二次定軸轉動。 另外無論在何種摩擦因數下,桿觸地端均無跳離地面的現象。 本文利用理論力學、常微分方程等相關知識,分析了考慮摩擦的剛性直桿傾倒的全過程,建立了完善的動力學模型,得到了直桿打滑角和反向角與摩擦因數的關系,同時利用直桿觸地端位移的表達式,得到了觸地端最終位移與摩擦因數的關系曲線,通過實驗驗證了部分現象,對以往的部分錯誤進行了糾正,并得到如下結論: (1)剛性直桿在自由傾倒過程中,無論桿與地面的摩擦因數為何值,桿觸地端在某一個傾角都會滑動; (2)當摩擦因數f∈(0,0.317)時,桿觸地端有靜止(即定軸轉動)、反向滑動和正向滑動三個階段;當摩擦因數f∈(0.317,0.370)時,桿觸地端有靜止(即定軸轉動)、反向滑動、靜止(即第二次定軸轉動)和正向滑動四個階段;當摩擦因數f∈(0.370,+∞)時,桿觸地端有靜止(即定軸轉動)和正向滑動兩個階段; (3)均質剛性直桿在自由傾倒過程中,無論桿與地面的摩擦因數為何值,桿觸地端都不會跳離地面。 由于篇幅所限,本文沒有再考慮動靜摩擦因數不等的情況,如果考慮,思路基本不變,只需對各運動模型中的摩擦因數作區分,可以得到新的結論,并且更接近真實的運動情況,但同時也會帶來求解與表述上的困難,此外本文的實驗也以定性驗證為主,還可以在更好的實驗條件下對更多的結論進行驗證。1.2 平面運動過程
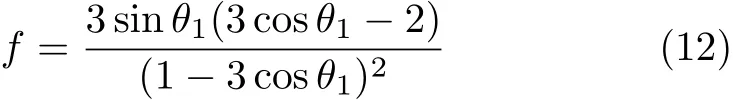
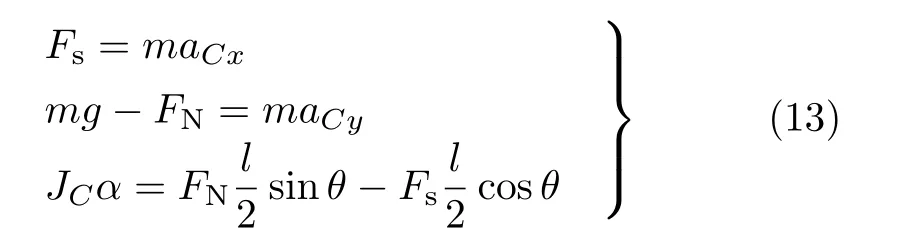

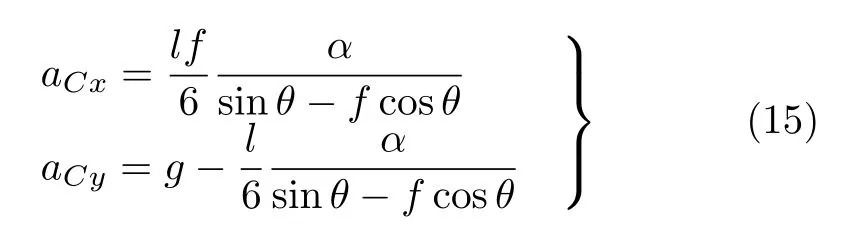
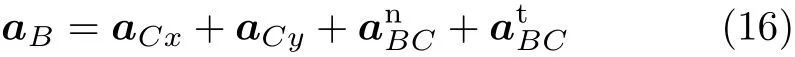
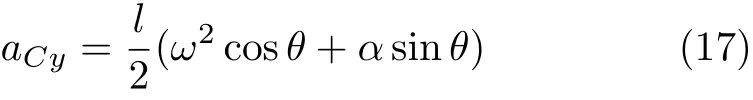
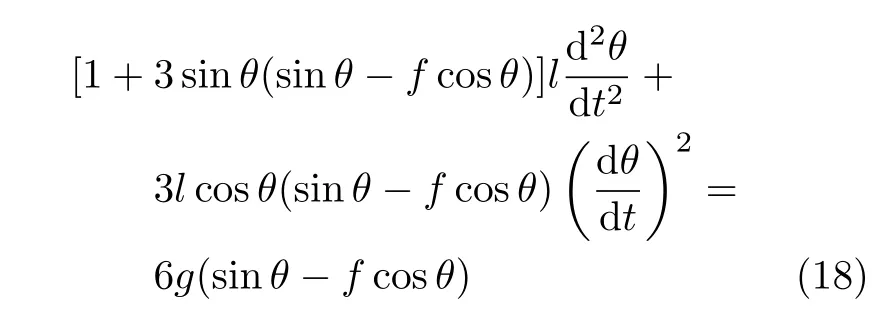
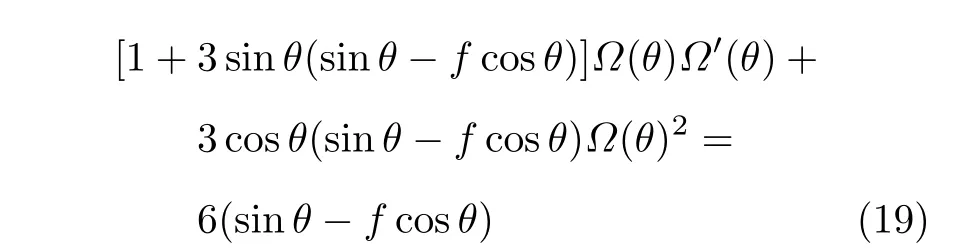
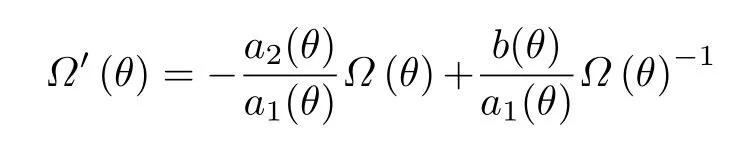
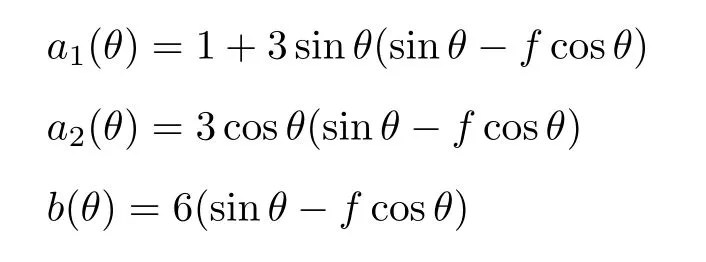
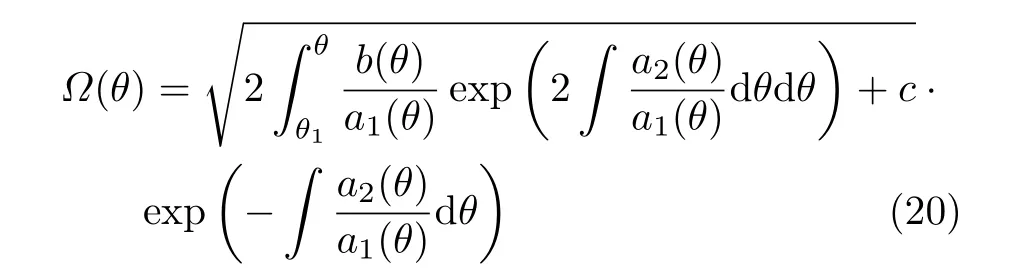
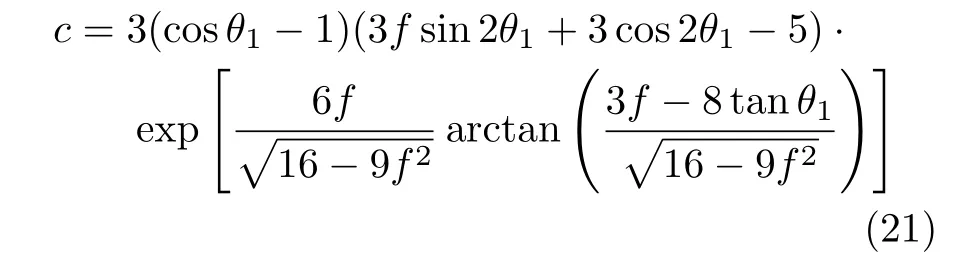
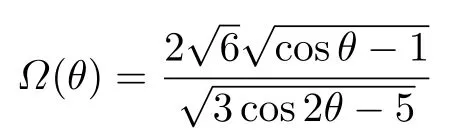
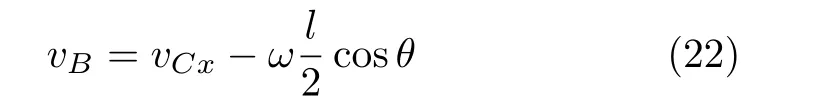
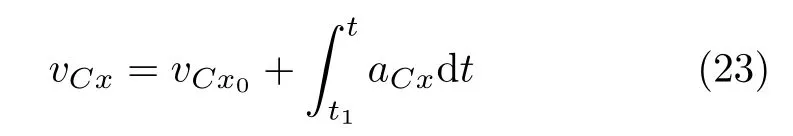
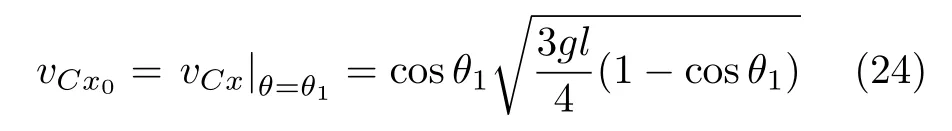
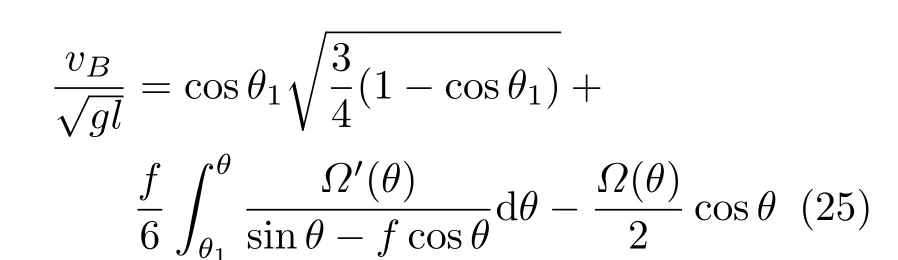
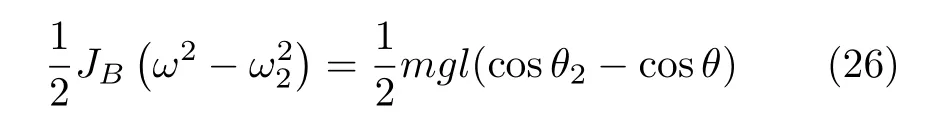
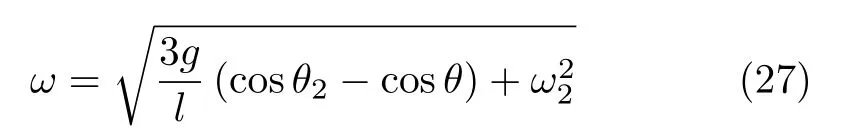
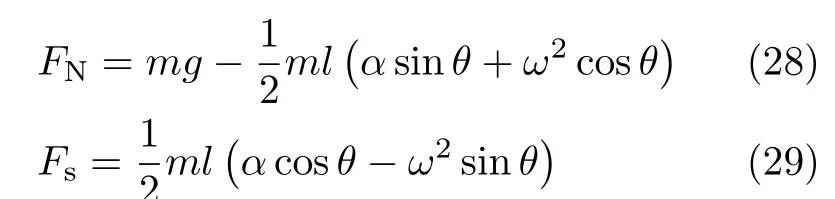
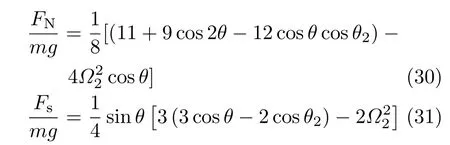

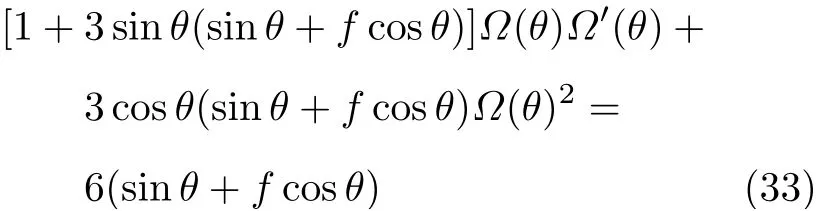
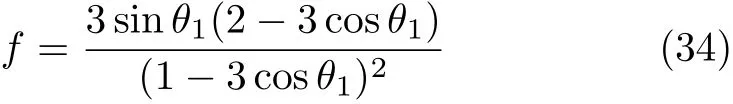
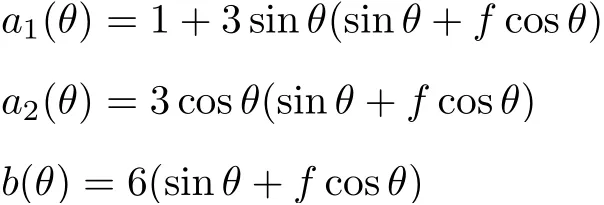
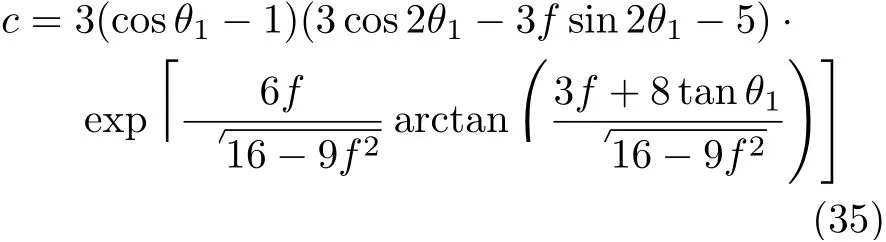
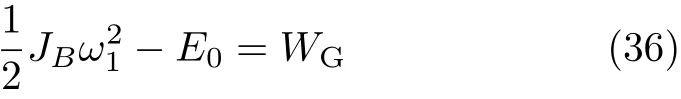
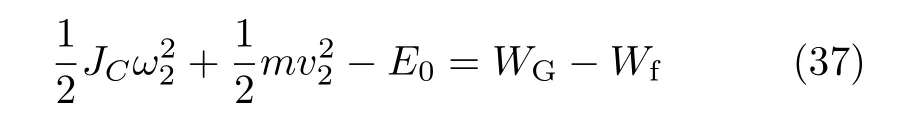
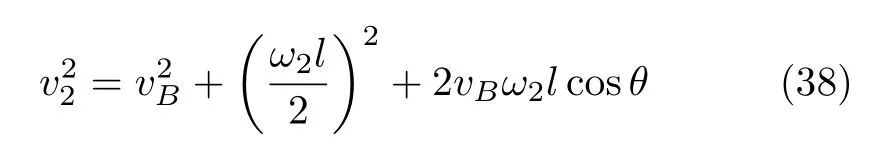
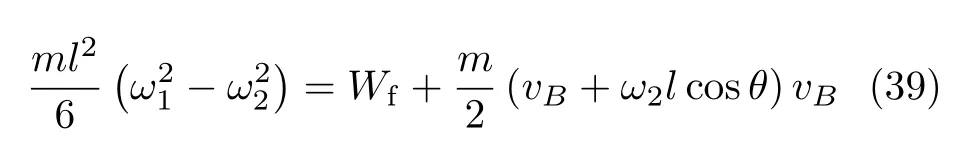

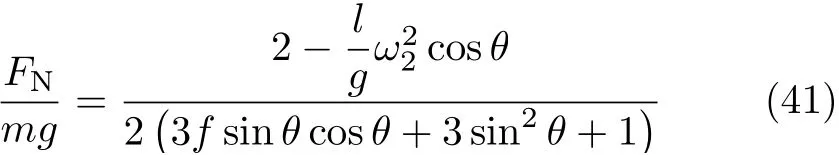
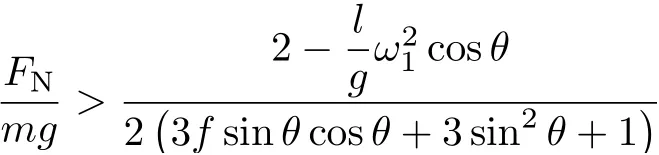
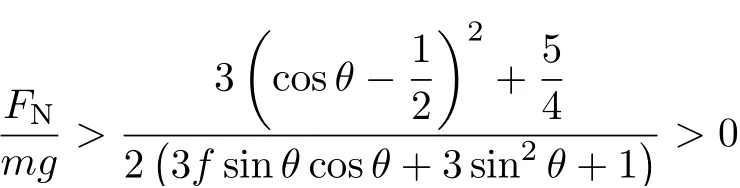
2 觸地端位移分析
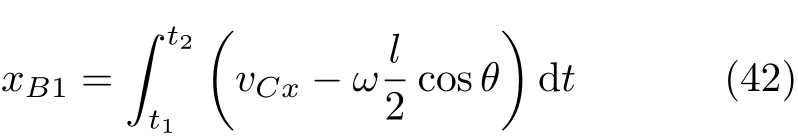
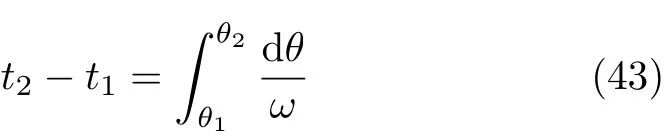
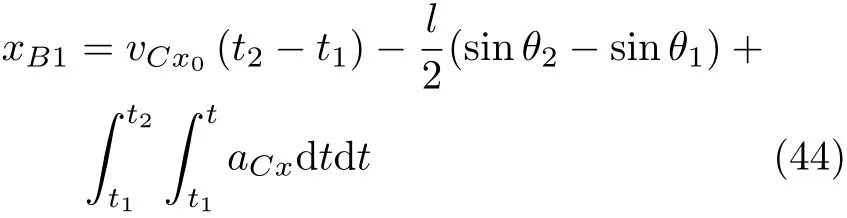
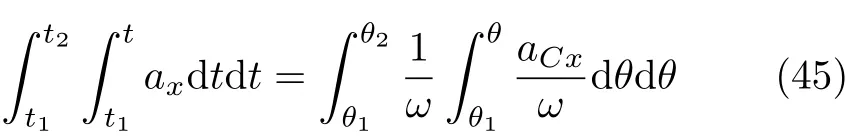
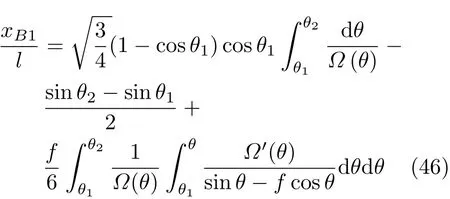
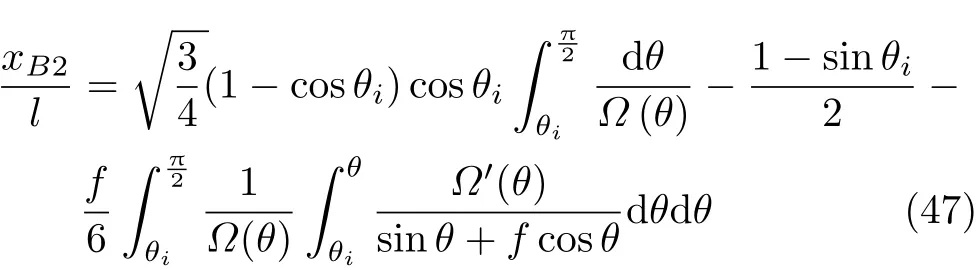

3 實驗驗證
3.1 摩擦因數的測量
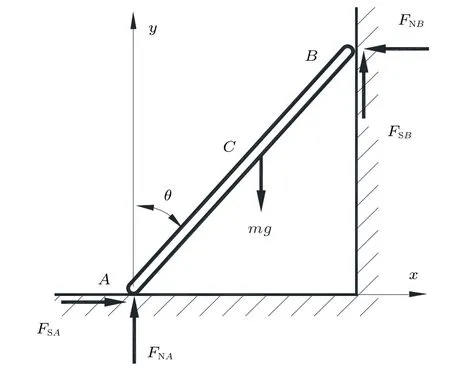

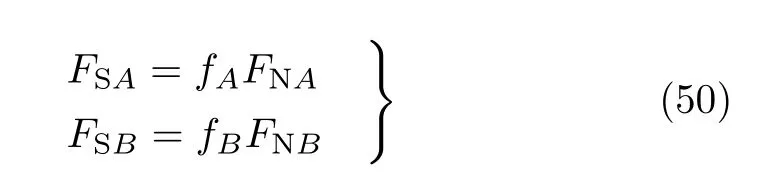
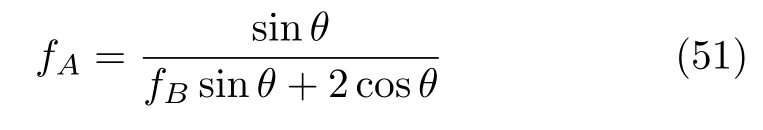


3.2 觸地端初次滑動臨界角測試

3.3 觸地端運動狀態驗證


4 結論與展望

