用給定轉角分步實現剛體任意有限轉動的研究
鞏浩然 武 迪 龔勝平 李俊峰
?(清華大學航天航空學院,北京100084)
?(北京航空航天大學宇航學院,北京100191)
1775年,Euler[1]使用球面幾何方法首次證明了任意有限剛體旋轉運動都可以等價為一次繞某固定轉軸的定軸轉動。同時歐拉創造性地提出了歐拉角的概念,即剛體的任意姿態運動,都可以分解為3次繞固連系坐標軸的定軸旋轉之疊加(連續兩次的轉軸不可相同),經典的分解順序包括依次繞z-x-z軸旋轉的進動、章動、自轉,和依次繞z-y-x軸旋轉的偏航、俯仰、滾轉等。這種分解方法清晰易懂、方便可視化,尤其為工程應用帶來了諸多便利。1973年,NASA研究人員Davenport[2]在歐拉角正交分解的基礎上,研究了將剛體轉動分解為幾次繞非正交軸旋轉的可行性及分解方法。2003年,Wittenburg等[3]進一步將問題拓展到一般的螺旋位移運動分解。
這幾種姿態運動的分解雖有不同,但基本出發點一致:已知剛體某有限轉動并給定幾根轉動軸(正交或非正交的),將該有限轉動分解為繞這幾根給定軸的轉動之疊加。與上述研究的問題不同,本文研究的問題則是:已知剛體某有限轉動,給定旋轉角度大小,問該轉動是否可以分解為一系列轉角為給定角度的定軸運動(轉軸的方向自由選取)之疊加。為了使問題闡述得更清楚形象,用三維歐式空間中的質點位移做個類比。上述已有的研究類似于已知質點某有限位移,給定幾個空間方向(正交或非正交),將該有限位移分解為沿這幾個給定方向的位移之和。而本文的研究問題則類似于,已知質點某有限位移,給定單步運動步長,是否可以將該有限位移分解為一系列步長為給定步長的位移運動之疊加。
舉例來說,假設剛體需要繞z軸轉動10°,如限定單次轉角只能為5°,則可以拆分為2次繞z軸的旋轉之和,如限定單次轉角只能為2°,則可以拆分為5次繞z軸的旋轉之和,如限定單次轉角為3°,那么幾次繞z軸的轉動就無法實現需求,這時還需要去尋找z軸之外的其他轉軸,將目標轉動拆分為幾次轉角為3°的轉動之和。
本問題屬于較為經典的姿態運動學問題,既有其力學理論價值,也有工程實踐意義。例如在依靠步進電機旋轉的機構中,步進電機的轉軸方向可以任意變化,但步進電機的最小步長有限制,對于某些微型步進電機,最小單步步長可以達到18°,此時依靠步進電機的姿態運動就不得不考慮本文研究的問題。此外,本文作者也在做空間多體系統通過關節運動實現姿態機動的研究,在這類問題中,有些情形下多體系統姿態運動的轉角是一定的,而轉軸方向的選取則有較大自由,本文所研究的問題也與之密切相關。
如圖1所示的多體結構太陽帆,其姿態固連系建立在中心十字架上,1和3號帆可以繞x軸同步旋轉,2和4號帆可以繞y軸同步旋轉。整個帆可以看做一個由中心十字支架、1和3號帆、2和4號帆組成的3剛體系統,通過帆面的旋轉,可以實現中心十字支撐(即姿態固連系)的姿態變化。當1和3號帆位于Oxy平面上時,2和4號帆的旋轉會引起整星姿態(即固連在中心十字支撐上的固連系姿態)繞y軸反轉,而當1和3號帆與Oxy平面形成一個夾角θ1時,2和4號帆的旋轉也會引起整星姿態變化,但由于失去了對稱性,此時整星轉軸不再是y軸,而是偏離y軸的α軸。考慮如下一組轉動:初始時刻4片帆面全部位于Oxy平面內,首先,1和3號帆旋轉θ1后保持不動,接著,2和4號帆旋轉nπ后保持不動(此時2和4號帆仍位于Oxy平面內),最后1和3號帆反轉θ1回歸原位。經歷了這樣一組轉動后,太陽帆的構型與初始時一致,但整星姿態發生了變化,其姿態變化四元數可以由3次轉動疊加得到
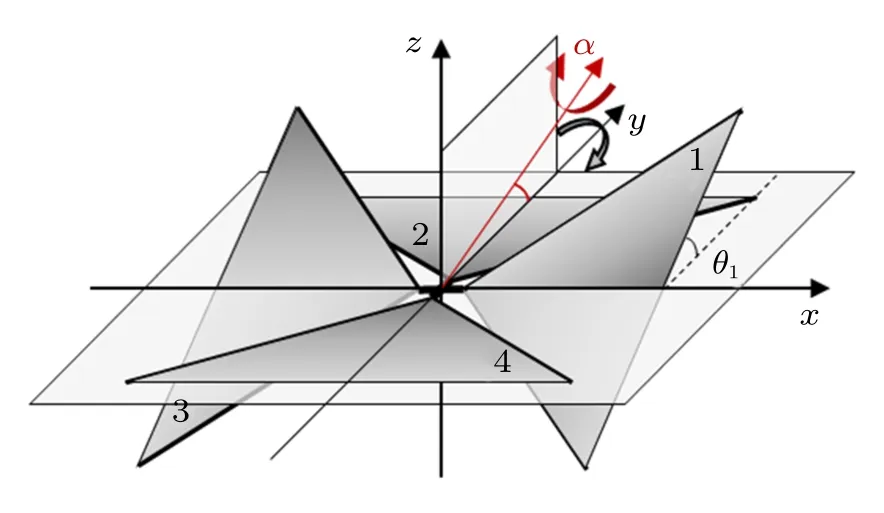
圖1 由4片直角三角形帆面及相應支撐桿構成的太陽帆

其中,°表示四元數相乘運算。a是第一次轉動后,整星繞x軸反轉的角度,與θ1成正比,b是第二次轉動后,整星繞α軸轉動的角度,與nπ成正比,c是α軸抬離Oxy平面的角度,也是θ1的函數。固定b,而令a變化,式(1)顯示,整星姿態變化的轉角是一定的,而轉軸的方向可以是Oyz平面內的任意方向(通過選取恰當的a)。試圖通過一系列這樣的3步組合轉動實現太陽帆的任意姿態機動,這就不可避免地要回答一個問題:在多步姿態轉動中,轉角固定,而轉動方向可在一定范圍內選取,能否拼出任意想要的姿態變換?在這個太陽帆的問題中,轉軸的方向被限定在了Oyz平面內,使得問題更加復雜,這里先來看看轉軸方向可以任意選取時的情況。
在下一節中,使用姿態四元數作為主要工具,通過構造性的證明方式,證明上述分解的可行性,并給出分解方法。
1 問題描述及證明
1.1 問題的數學描述
對于某一轉軸方向為e,轉角為m的給定剛體定軸轉動(用姿態四元數描述)
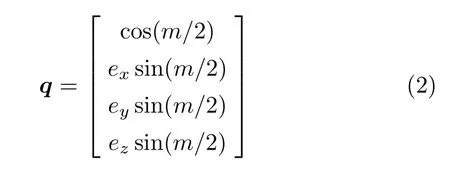
是否可以通過一系列轉角n i給定,轉軸方向e(i)任意的定軸轉動
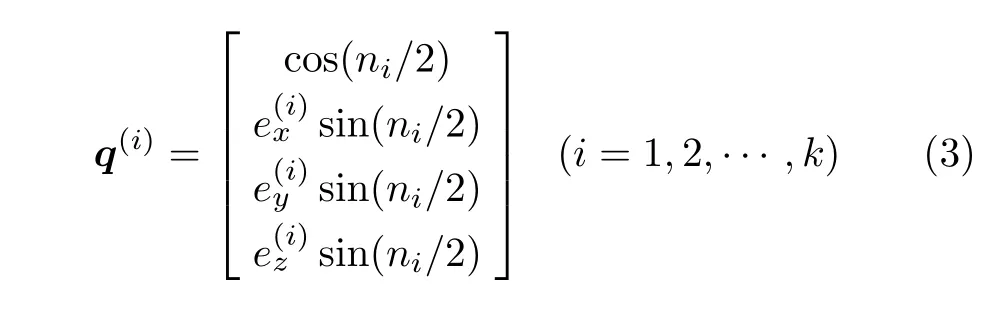
拼湊而成?即是否可以通過恰當選取每次轉動的轉軸e(i)使得q=q(1)°q(2)°...°q(k)?
1.2 一種構造性證明
首先,上述問題的答案是肯定的,通過有限次轉角依次為n1,n2,···n k的定軸轉動,一定可以拼接出某一轉軸方向為e,轉角大小為m的定軸轉動,且一定可以在k次內完成,這里k表示滿足的最小整數。具體分解方法如下:
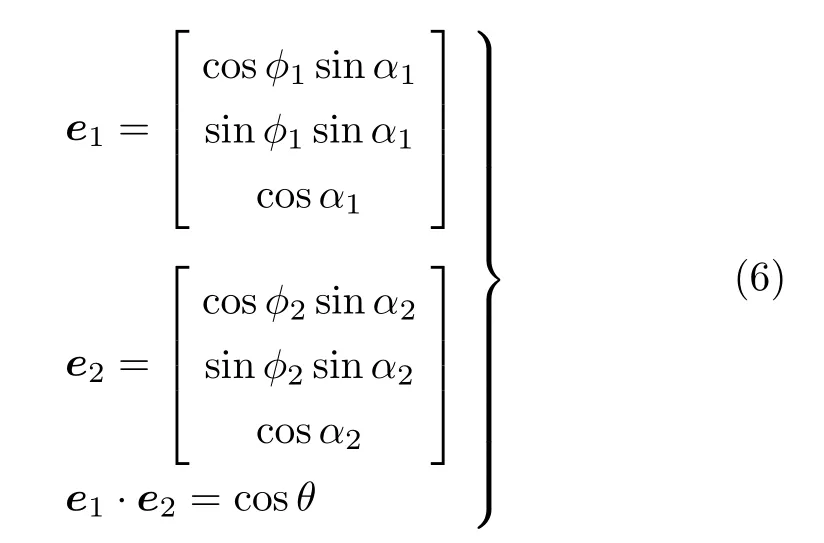
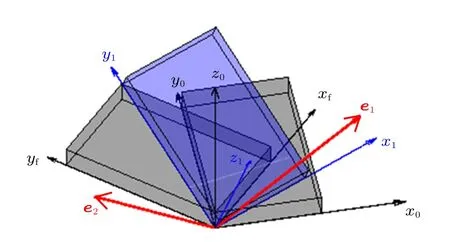
(1)當m≥n1+n2時,取轉軸方向e(1)=e,靠近目標姿態,設在第i?1步后,距離目標姿態的一次轉動轉角為m i-1,如m i-1≥n i+n i+1,繼續取轉軸方向e(i)=e;如m i-1 (2)當m 不失一般性地,可以假設目標轉動q的轉軸e=[0,0,1]T,因為對于任意轉動,總能找到一個旋轉坐標系,使得在該坐標系下,轉軸方向為[0,0,1]T。令兩次轉動之疊加等于目標轉動 注意,這里e1,e2并非在同一坐標系下的兩個方向,e1是在空間慣性坐標系下的方向投影,e2則是基于e1轉動之后的剛體固連系上的方向投影。方程(4)可展開為 因為單位四元數模為1的天然約束,如式(5)所示的4個標量方程中,只有3個獨立方程,而獨立未知量則有4個(每個轉軸方向含2個獨立未知量),故方程(4)的解并不唯一。設 代入方程(5)整理可得四個解 上述4個未知量的解只有3個是獨立的,方便起見,取式(7)~式(9)為一組解,觀察該解,式(8)和式(9)說明e1,e2在z方向的分量可以確定,式(7)說明e1,e2兩方向的夾角可以確定,滿足式(7)~式(9)均為可行解。解存在的條件為 與情況(2)的條件相符。 設目標剛體姿態運動為繞初始z軸旋轉2π/3,依靠步進電機實現該運動,假設該步進電機的轉軸方向可以任意取定,最小單步轉角為π/5。根據上一節的討論,由于2π/3>π/5+π/5,首先令步進電機轉軸方向取為z軸,經1次轉動后距離目標姿態2π/3?π/5=7π/15,因為7π/15>π/5+π/5,繼續令步進電機轉軸方向為z軸,經第2次轉動后距離目標姿態7π/15?π/5=4π/15。此時因4π/15<π/5+π/5,將m=4π/15,n i=π/5代入方程(7)~方程(9)可得 滿足式(12)的解均為可行解,不妨取兩次轉動的四元數為 綜上,步進電機的4次定步長轉動,即可實現目標姿態運動,圖2為第3和第4兩步旋轉分解的示意圖。初始姿態固連坐標系(經過前2步轉動后的剛體固連坐標系)Ox0y0z0,目標姿態固連坐標系Oxfyfzf,經過前3次旋轉后的剛體固連坐標系Ox1y1z1。為了展示清晰,除坐標系外,還畫出了一個假想的手機狀剛體。圖中e1,e2為第3和第4兩次旋轉的旋轉軸(均已轉換到第2次旋轉后的剛體固連坐標系下)。 圖2 實驗案例中的旋轉分解示意圖 關于姿態運動分解的過往研究,多集中于給定“基方向”,如何選擇適當的轉角以實現任意姿態變換;本文則是給定旋轉步長,自行尋找適合的“方向”以實現任意姿態變換。本文通過四元數運算證明,通過有限次旋轉步長給定、旋轉軸方向任選的定軸旋轉,可以實現任意的剛體空間旋轉。這種分解的可行性將為姿態運動學的理論分析和實踐運用帶來一些新思路。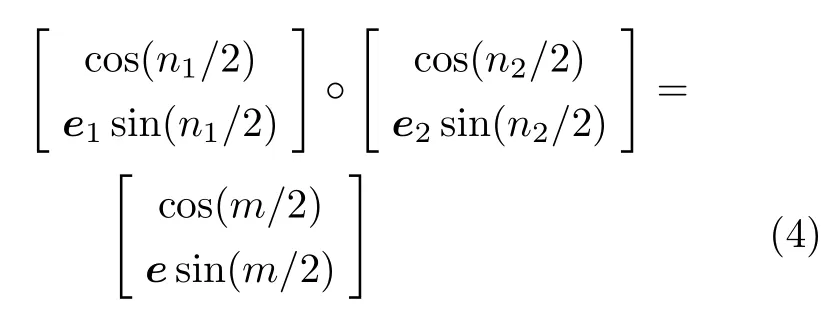
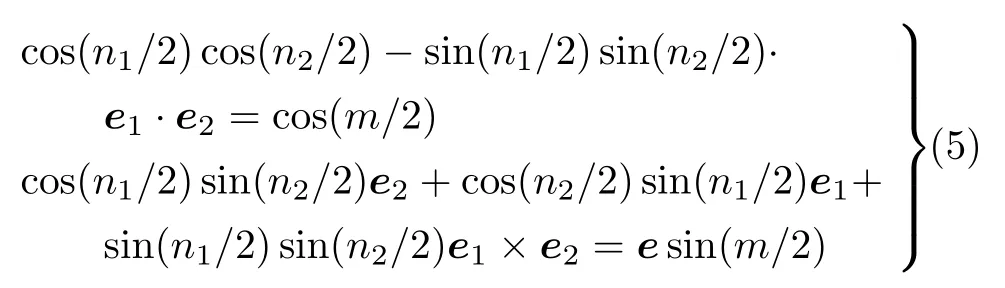
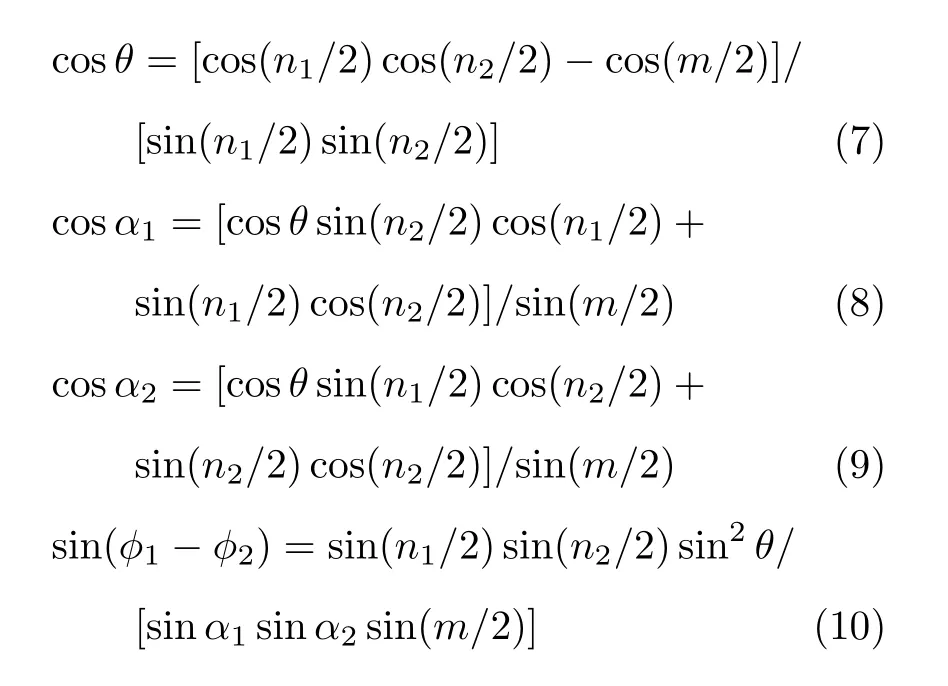
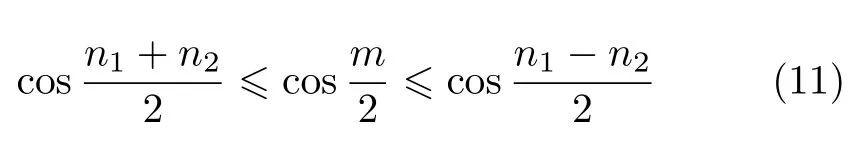
2 例子
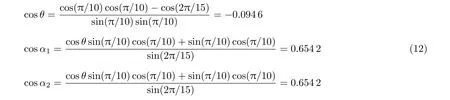
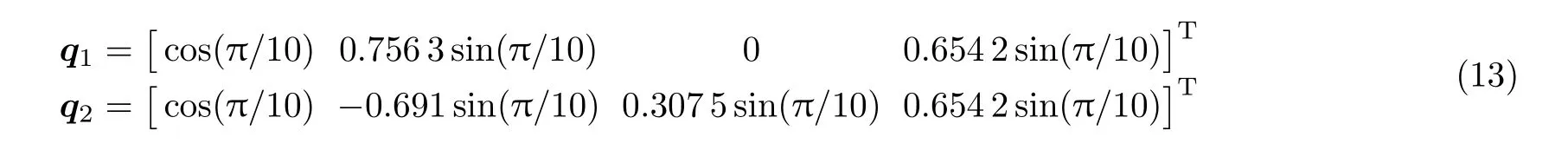
3 結論

