一種非平穩噪聲背景下的線譜相干檢測方法

馬世龍，徐雅南

（杭州應用聲學研究所，浙江 杭州 310012）

0 引言

艦艇目標航行會向水中輻射聲信號，艦艇機械結構、螺旋漿等周期往復運動，會產生大量線譜信號，通過檢測線譜信號可實現對艦艇目標的被動探測[1-4]。常見的線譜檢測方法多是以離散傅里葉變換（Discrete Fourier Transformation，簡記為DFT）為基礎的衍生算法。如平均周期圖法，該方法對接收數據進行分段DFT變換，取變換后復序列的模幅度信息，計算功率譜估計值，實現線譜信號檢測[5-10]。文獻[11-19]在 DFT基礎上，構建二元假設檢驗問題，并依據信號統計特性，推導得到廣義似然比檢測器，進行線譜信號檢測。Kay等對周期圖譜估計結果進行背景能量歸一化，從而構建了一種具有恒虛警特性的線譜檢測器，由于該方法對整段接收數據進行DFT處理，因此對硬件處理性能要求較高，且估計得到的功率譜背景起伏方差較大[11]。Wan等根據分段 DFT估計得到功率譜統計特性，構建了一種廣義似然比檢測器，該方法線譜檢測性能優于平均周期圖法，但同樣不能獲得分段 DFT間的線譜相干處理增益[12]。Wang等補償各分段DFT數據間的相位差，利用相位補償后的數據構建了一種具有恒虛警特性的線譜檢測器，可獲得分段 DFT數據間的線譜相干處理增益[13]。

上述 DFT類線譜檢測方法主要構建于分段DFT基礎上，檢測過程中均利用DFT幅度信息。平穩噪聲背景下，DFT頻率分辨帶寬內線譜信號幅值持續高于噪聲背景，此時對分段 DFT結果進行時域相加累積可獲得較優的累積增益。但實際水聲干擾環境中聲場噪聲背景起伏較大，常常表現為時域非平穩噪聲。非平穩噪聲背景下，對分段 DFT累積過程中，不可避免地引入非平穩噪聲背景中短時出現的強幅值噪聲，使積分結果中線譜信噪比大幅降低，性能急劇惡化。針對上述問題，本文提出了一種適用于非平穩噪聲背景的線譜相干檢測方法。相比常規 DFT類線譜檢測方法，所提方法在非平穩噪聲背景下受背景噪聲幅度起伏的影響小，對相位穩定的線譜信號具有更好的線譜檢測性能，且能夠獲得對線譜信號的相干處理增益。

1 數據模型

含有線譜信號的時域采樣數據記為x( n)，將x( n)分為多個數據段，每段含有N個數據點，第l分段數據：

圖1 時域接收數據分段Fig. 1 Time-domain received data segmentation

2 常規線譜檢測方法

1）平均周期圖法。

平均周期圖法對 Xl( k)求取模值，舍棄相位信息，之后對各分段模值進行平方累加，計算得到功率譜估計值，以檢測線譜信號。平均周期圖法計算表達式為

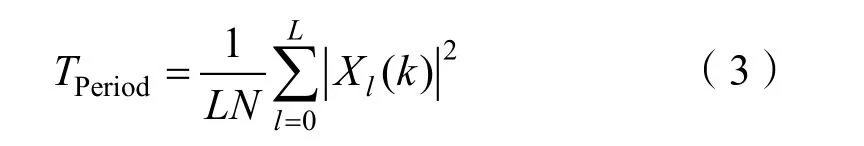
2）CGLRT方法。

文獻[13]所述相干廣義似然比檢測器（Coherent Generalized Likelihood Ratio Test，簡記為 CGLRT），對各分段DFT數據分別補償相位exp(j2πΔl)，使各段數據中信號相位對齊，噪聲相位保持隨機，對補償相位后的各分段數據進行累積，可獲得對信號相干處理增益。CGLRT方法檢測統計量表達式為

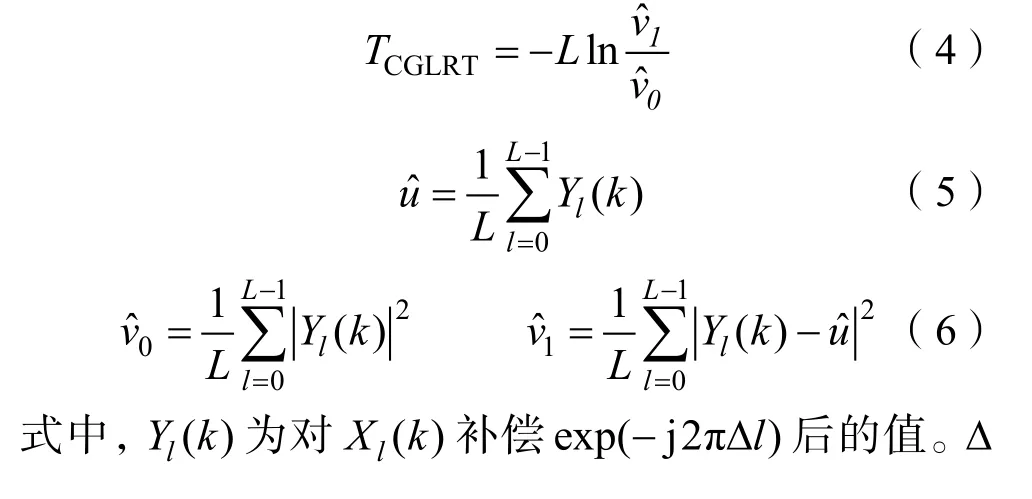
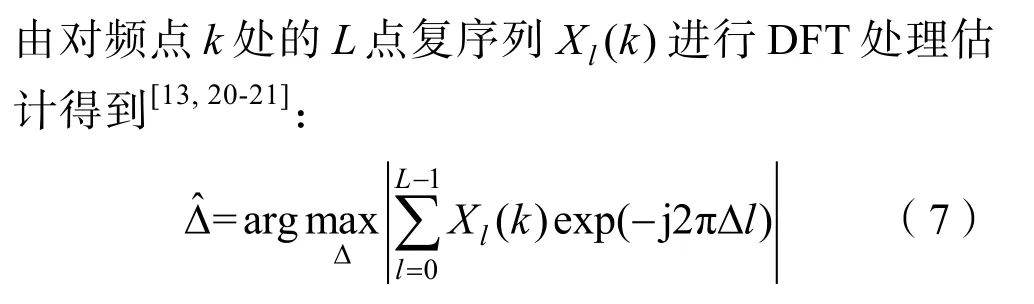
上述方法均利用分段 DFT變換結果 Xl( k)的幅度信息，進行幅值累加或能量累加。平穩噪聲背景下，DFT頻率分辨帶寬內線譜信號能量持續高于噪聲背景，即 Xl( k)中信號能量高于噪聲背景能量。此時，對各分段數據累加可獲得對信號的累積增益。非平穩噪聲背景下，噪聲背景幅度往往會出現短時劇烈起伏，如第l0數據段 Xl0(k)中噪聲能量遠高于其它數據段 Xl( k), l≠l0噪聲能量，具有較低的信噪比。此時，對各分段DFT數據 Xl( k)累加則會引入噪聲幅值較大的數據段 Xl0(k)，使累積結果TCGLRT和TPeriod中線譜信噪比大幅降低，線譜檢測性能惡化。由此，降低非平穩噪聲幅值短時劇烈起伏的影響，有助于改善非平穩噪聲背景下的 DFT類線譜檢測方法性能。

3 改進的CGLRT線譜相干檢測方法

為改善時域非平穩噪聲幅度短時劇烈起伏對DFT基線譜檢測方法的影響，可對不同分段DFT結果進行幅度歸一化，實現時域幅度均衡。但對于僅包含線譜幅度信息的平均周期圖法，幅度歸一化會損失線譜信息，而無法檢測線譜。為通過幅度歸一化降低時域非平穩噪聲起伏的影響，本文主要思路是充分利用目標線譜相位穩定的特性，構建歸一化幅度的線譜相位相干檢測器，以保留線譜信息，實現時域幅度均衡，同時可獲得對線譜信號的相干處理增益。具體實現過程為：首先，對CGLRT進行等價變換，推導出以單一 Xl( k)為變量的簡化檢驗統計量表達式；之后，在該表達式基礎上歸一化幅度，進而提出一種改進的CGLRT線譜相干檢測方法（Modified Coherent Generalized Likelihood Ratio Test，簡記為 MCGLRT）。

3.1 CGLRT等價變換

結合式（5）和式（7），可得：

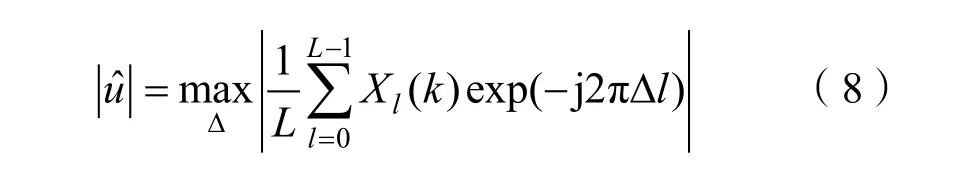
3.2 幅度歸一化

4 仿真分析

本文通過仿真分析，比較了平均周期圖法、CGLRT及所提MCGLRT方法在平穩噪聲和非平穩噪聲背景下的性能。為描述背景噪聲時域幅度非平穩程度，參照文獻[22]廣義功率譜平坦系數，定義背景噪聲時域幅度起伏平坦系數γp為

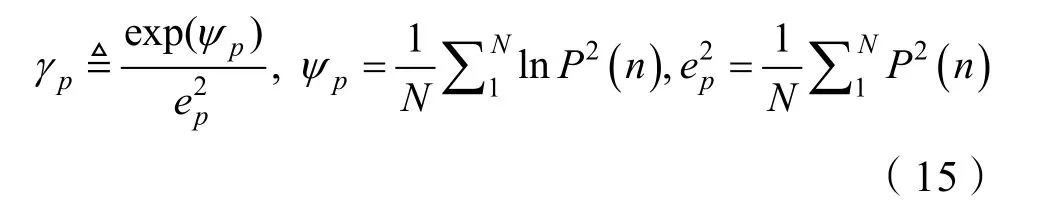
4.1 平穩噪聲下性能分析

仿真條件：為比較分析平穩噪聲下平均周期圖法、CGLRT方法、所提MCGLRT方法的性能，采用蒙特卡洛法比較分析3者的線譜檢測性能。平穩高斯白噪聲背景中存在頻率為400 Hz線譜信號，背景噪聲時域幅度起伏平坦系數為 γp= 1。采樣數據時長8 s，采樣率為10 kHz。3者方法中均將接收數據分為80段，每段1 000點數據。虛警概率取10-2，蒙特卡洛次數為5 000。圖2為3種方法的檢測概率隨信噪比變化曲線，信噪比為線譜信號功率與噪聲功率之比。

由圖2所示，相同檢測概率下，所提MCGLRT方法所需SNR高于CGLRT方法約0.8 dB，主要因為所提MCGLRT方法幅度歸一化過程中損失了一定線譜信息，檢測性能略遜于CGLRT方法。但所提MCGLRT方法能夠充分利用相位信息，可獲得對線譜信號相干處理增益，故相同檢測概率下，要優于平均周期圖法約2 dB。

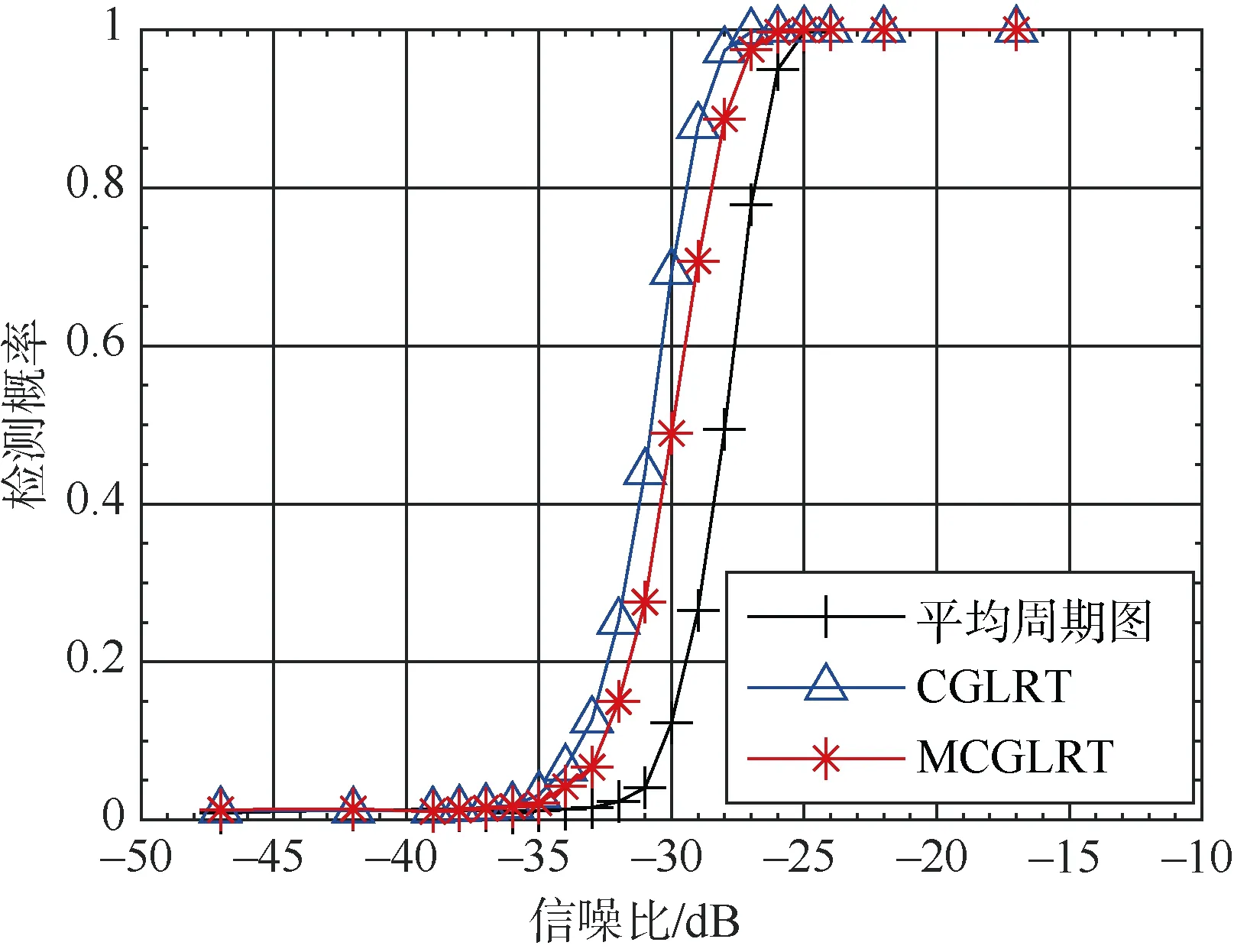
圖2 檢測概率隨SNR變化曲線（ γ p =1）Fig. 2 Curves of detection probability vs. SNR （ γ p = 1）

4.2 非平穩噪聲下性能分析

仿真條件：為仿真分析非平穩噪聲背景下各方法的性能，在前述仿真條件基礎上改變背景噪聲時域幅度起伏程度，時域幅度起伏平坦系數分別為 γp=0.87和 γp= 0.57兩種情況下波形如圖3所示。保持背景噪聲起伏包絡不變，仿真分析3種方法的檢測概率隨信噪比變化曲線如圖 4，其中信噪比為采樣時間內線譜信號功率與噪聲平均功率之比。信噪比為-35 dB和-30 dB時，3種方法的譜圖分別如圖5-8所示。

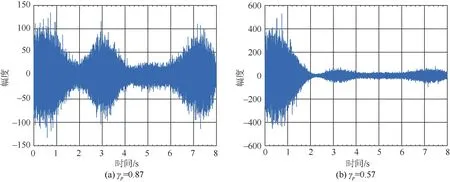
圖3 非平穩接收數據時域波形Fig. 3 Time-domain waveform of non-stationary received data

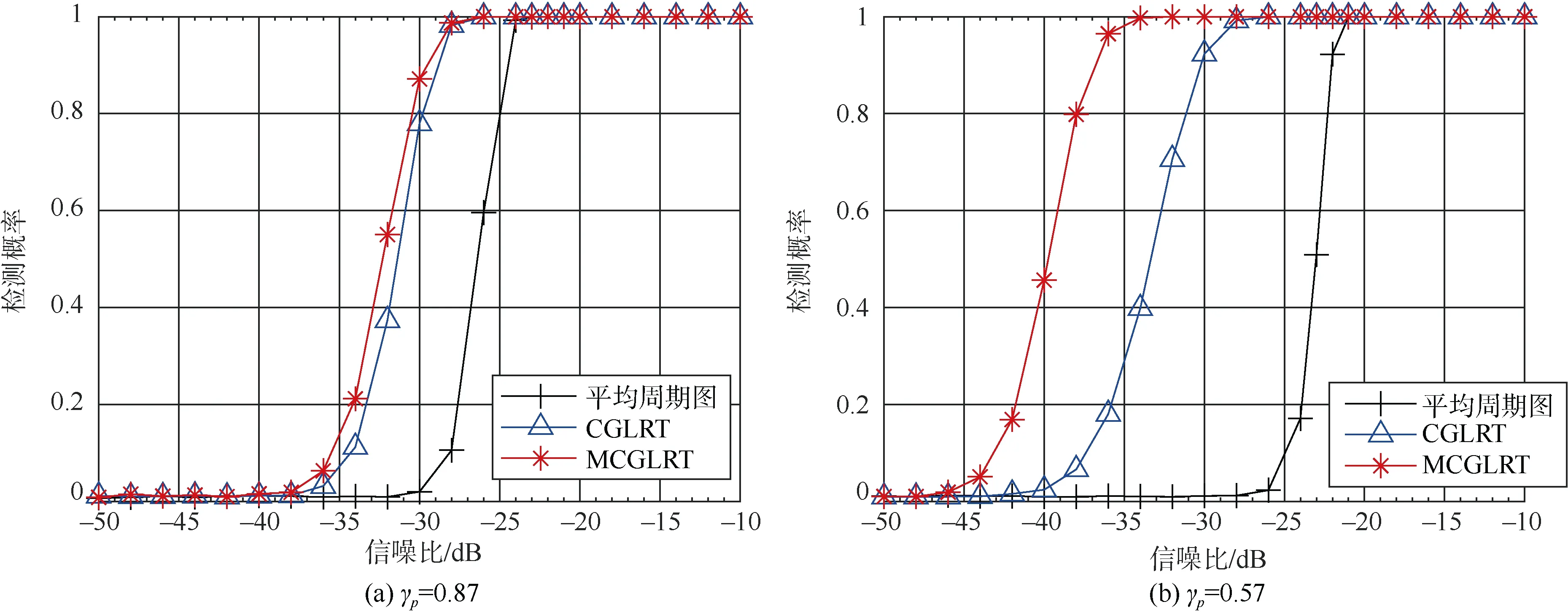
圖4 檢測概率隨SNR變化曲線（ γ p =0.87和 γ p =0.57）Fig. 4 Curves of detection probability vs. SNR（ γ p = 0.87和 γ p = 0.57）

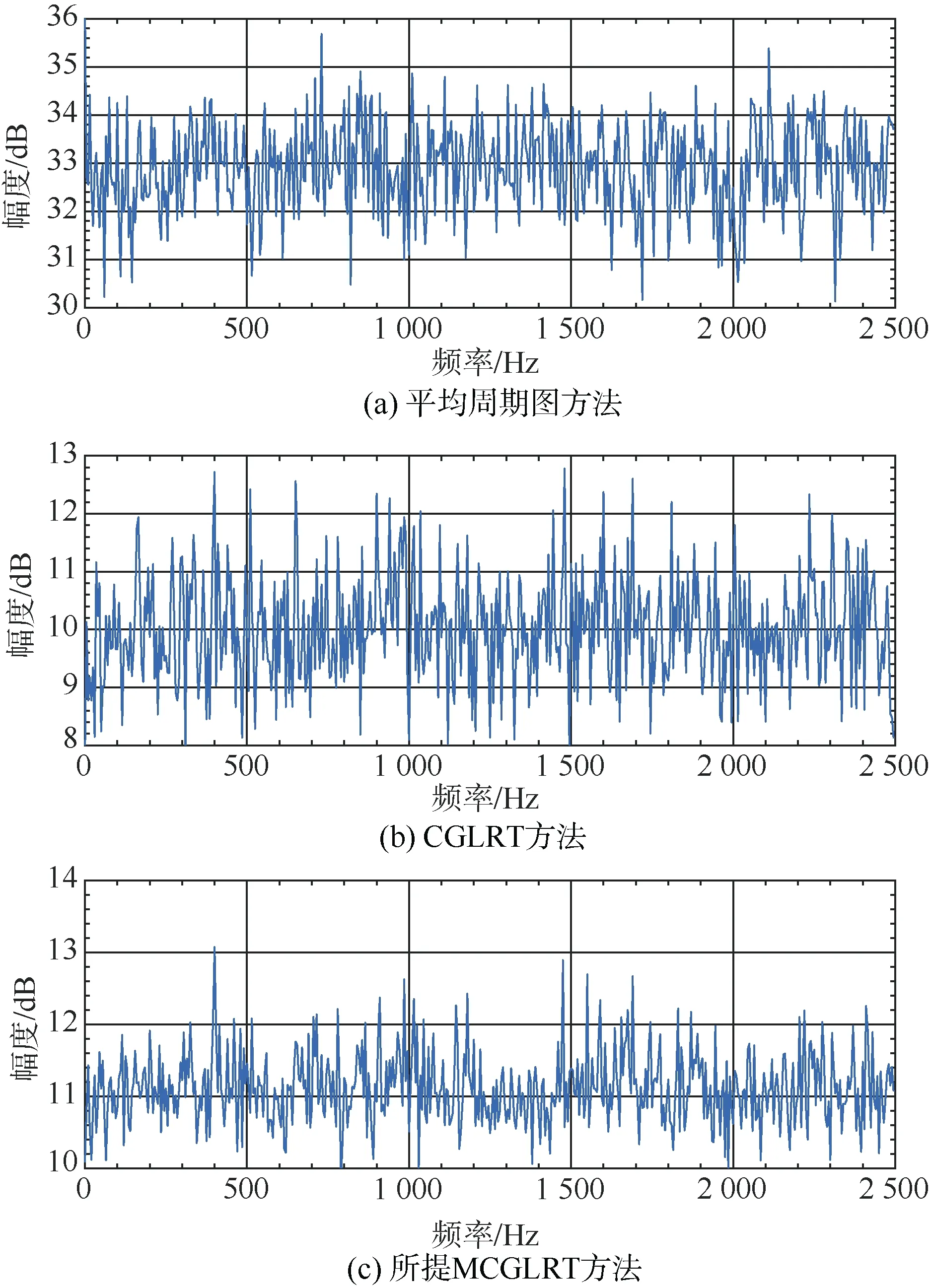
圖5 非平穩噪聲背景下譜圖（ γ p =0.87，SNR=-35 dB）Fig. 5 Spectrograms in non-stationary noise background（ γ p = 0.87，SNR=-35 dB）

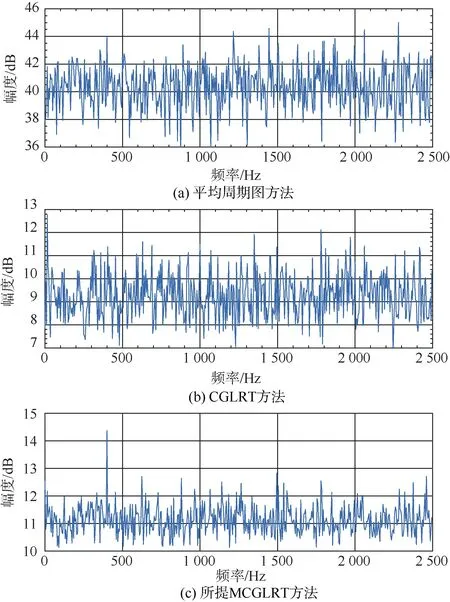
圖6 非平穩噪聲背景下譜圖（ γ p =0.57，SNR=-35 dB）Fig. 6 Spectrograms in non-stationary noise（ γ p = 0.57，SNR=-35 dB）

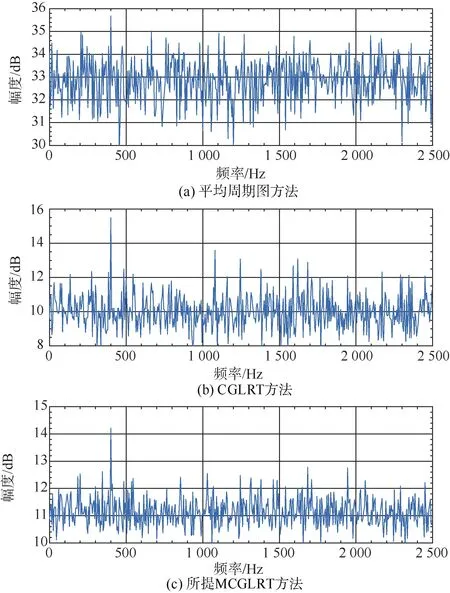
圖7 非平穩噪聲背景下譜圖（ γ p =0.87，SNR=-30 dB）Fig. 7 Spectrograms in non-stationary noise background（ γ p = 0.87，SNR=-30 dB）

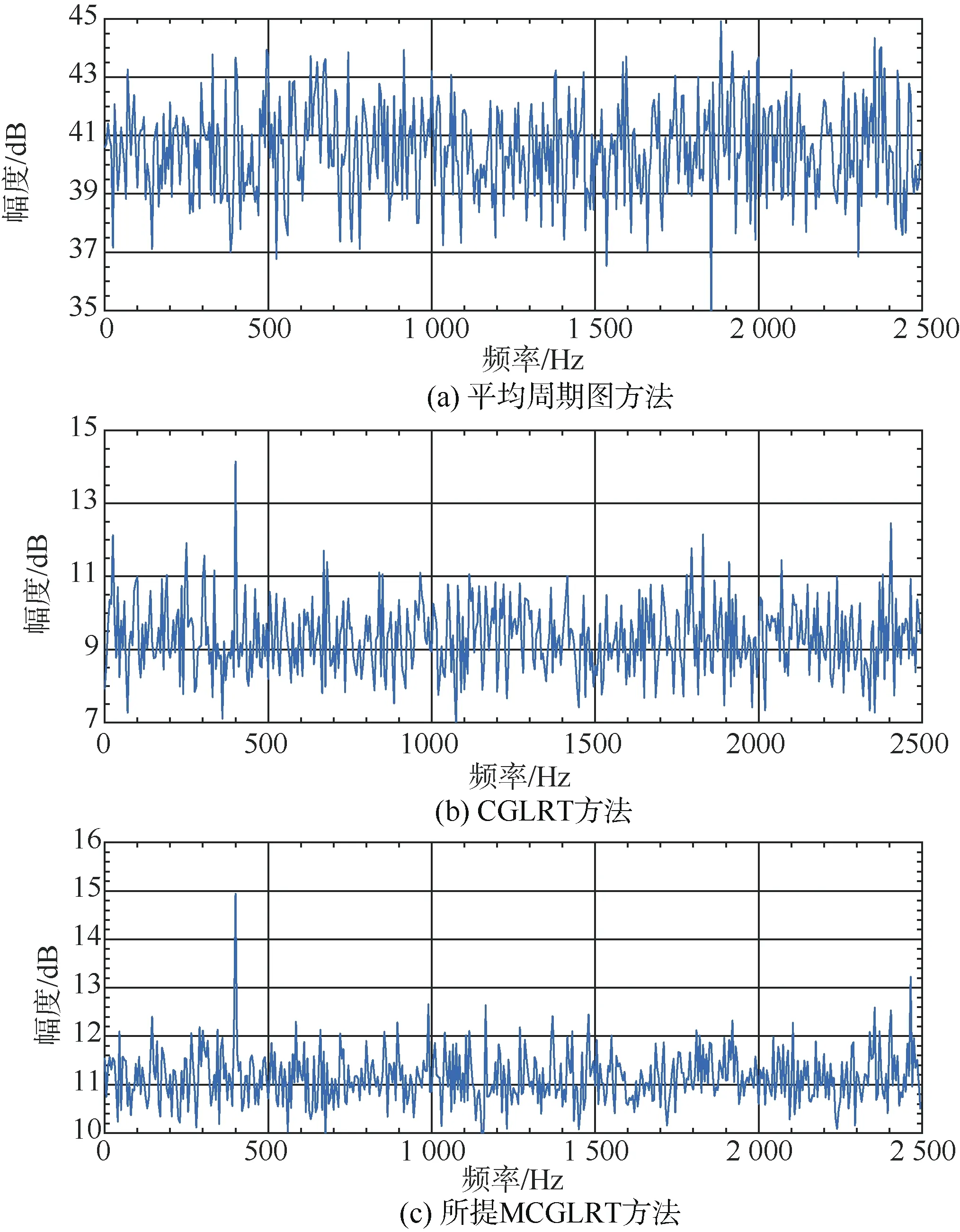
圖8 非平穩噪聲背景下譜圖（ γ p =0.57，SNR=-30 dB） Fig. 8 Spectrograms in non-stationary noise background （ γ p = 0.57，SNR=-30 dB）

如圖 4所示，上述γp= 0.87和γp= 0.57兩種非平穩噪聲背景仿真條件下，達到相同檢測概率，本文所提MCGLRT方法所要求的輸入信噪聲比優于CGLRT方法約0.9 dB和6 dB，優于平均周期圖法5 dB和15 dB。主要原因是平均周期圖法、CGLRT法中對接收數據的幅度信息進行累積，受噪聲背景短時劇烈起伏的影響，分段累積結果中線譜信噪比大幅降低；本文所提MCGLRT方法，對分段接收數據 DFT變換結果進行頻域幅度歸一化，受噪聲背景短時劇烈起伏的影響較小。此外，由圖5-8所示譜圖也可看出，信噪比為-35 dB時，所提MCGLRT方法相比平均周期圖法、CGLRT法具有更清晰的線譜譜峰，隨信噪比升高，平均周期圖法、CGLRT方法線譜譜峰趨于清晰。上述仿真結果表明本文所提MCGLRT方法在非平穩噪聲背景下具有更優的線譜檢測性能。

5 結束語

本文針對時域非平穩噪聲背景下常規 DFT基線譜檢測方法性能下降問題，推導了CGLRT的一種等價變換式，在此基礎上對分段 DFT結果進行幅度歸一化，提出一種改進的CGLRT線譜相干檢測方法，即MCGLRT方法。仿真結果表明，所提MCGLRT方法線譜檢測性能優于平均周期圖法。時域平穩高斯白噪聲背景下，所提MCGLRT方法線譜檢測性能略遜于CGLRT方法，但噪聲背景呈現短時劇烈起伏等非平穩特性時，線譜檢測性能優于CGLRT方法。