基于撓度分析的等截面連續梁合理邊中跨跨徑比

楊 毅

（中鐵二十三局集團第三工程有限公司 四川成都 611130）

1 引言

在房屋建筑和橋梁工程中，常遇到多跨連續梁的情況。與簡支梁相比，連續梁在中間支座處承受負彎矩，跨中正彎矩和撓度顯著減小，因此，相同跨徑下，采用連續梁可減小跨中梁截面尺寸[1- 2]。連續梁的跨徑布置有等跨和不等跨兩種形式[3]。雖然等跨連續梁施工較為方便，但由于其邊跨缺少轉動約束，邊跨支座的負彎矩（指邊跨內支座處）大于中間跨支座[4]。以滿跨均布荷載作用下的四跨等截面連續梁為例，邊跨支座的負彎矩約為中間跨支座的1.5倍，邊跨的最大正彎矩為中間跨的2.1倍，邊跨的向下撓度極值為中間跨的3.4倍[5]。

采用不等跨布置時，邊中跨跨徑比一般為0.6～0.8[6-7]，主要是為減小第1跨跨中彎矩和支座負彎矩。近年來，對連續梁橋的研究主要偏向于受力方面，而對撓度的研究較少，一般認為在滿足受力前提下，跨中最大撓度滿足相關規范要求的撓度限值即可。通過設置預拱度的方法可以抵消恒載的短期撓度，但考慮長期作用，恒載的長期撓度還會繼續增大，公路相關規范規定長期撓度為短期撓度的1.35～2.0倍[8]，而大跨徑預應力混凝土梁橋的病害之一為主梁跨中的長期撓度過大[9-11]。若能在設計之初，最大限度地減小主梁跨中最大撓度值，則長期撓度也會相應減小。從行車平順性考慮，連續梁的撓曲線越小越平緩，車輛行駛則更為舒適。

由文獻[12]可知，當邊中跨跨徑比接近0.8時，各支座負彎矩、各跨中最大正彎矩和各支反力值整體最小。本文以等截面連續梁在荷載作用下的撓曲變形值為研究對象，用奇異函數法推導出連續梁在均布荷載和集中荷載作用下的撓曲線方程，得出在不同總跨數和邊中跨跨徑比條件下，連續梁的撓曲變形隨跨數和邊中跨跨徑比的變化關系；以結構在均布荷載和集中荷載作用下各跨向上撓度極值和向下撓度極值整體最小為目標，綜合得出不等跨連續梁的合理邊中跨跨徑比，為連續梁的變形設計提供參考。

2 連續梁撓度求解

連續梁在荷載作用下的撓曲變形可采用初參數法、拉普拉斯變換、奇異函數法等方法求解。其中初參數法適用于一般情況，但對于有突變荷載情況，撓度計算公式在荷載突變處要分段表達而顯得較為繁瑣。奇異函數法可以得出任意荷載作用下撓曲線的統一表達式。將拉普拉斯變換與奇異函數相結合，使復雜加載條件下連續梁的變形求解更為簡單，本文采用奇異函數法求解連續梁的變形。

連續梁上作用有一段均布荷載和集中荷載（見圖1），其中q為均布荷載，Pj為作用在第j跨內的集中荷載，連續梁第i跨跨徑為li，坐標系統以梁的受力方向向上為正，以梁的變形（y）向上為正，用奇異函數表達距第1支座為x的點的連續梁跨內荷載分布 q（x）表達式：

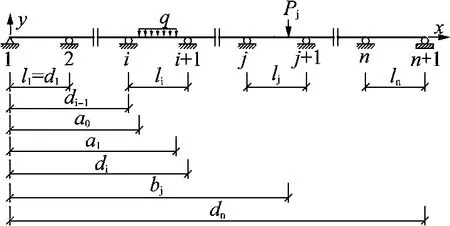
圖1 連續梁計算模型

式中：a0和a1分別為均布荷載的起點和終點至第1支座的距離；di為第i＋1支座至第1支座的距離；Ri為第i支座的支反力；bj為第j跨內集中荷載至第1支座的距離。對（1）式進行兩次積分，可得到連續梁的彎矩表達式：

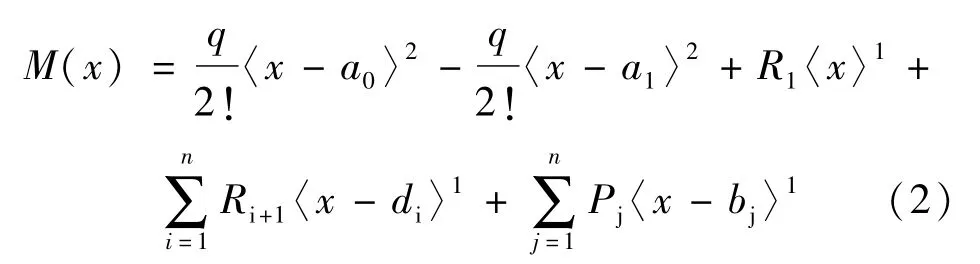
小變形情況下，梁的撓曲線近似微分方程為：

式中：EI為連續梁截面的抗彎剛度。對式（3）進行兩次積分，可得連續梁撓曲線方程：

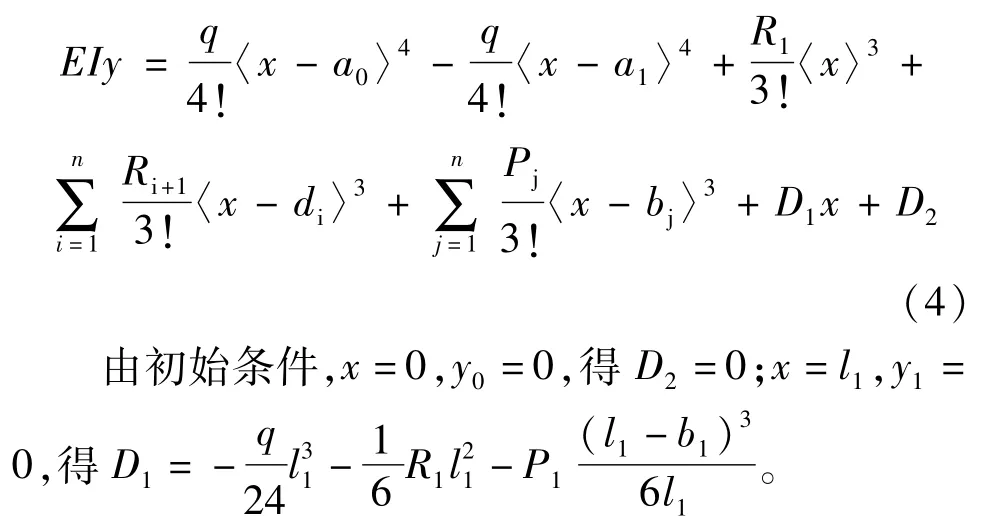
本文研究滿跨均布荷載和單個集中荷載作用下連續梁的受力情況，有a0＝0，a1＝dn，在第j跨上作用有集中荷載Pj，則式（4）變為：

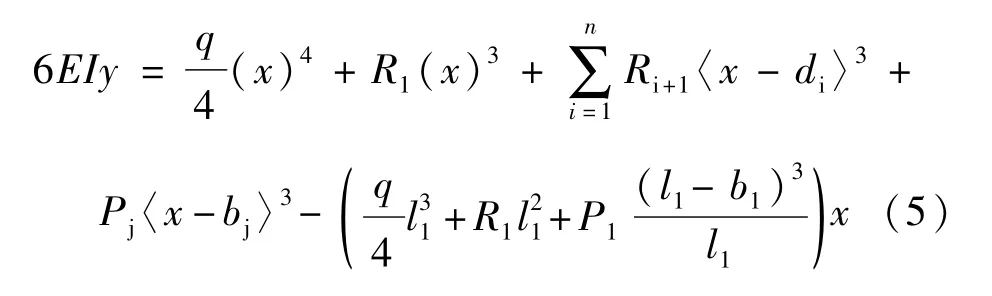
令連續梁的兩邊跨跨徑相等，則l1＝ln，其余中間跨的跨徑相等，其值為l，則邊中跨跨徑比為：α＝l1／l。根據其余n－1個支承處豎向位移等于0的條件，可得出如下n－1個方程：

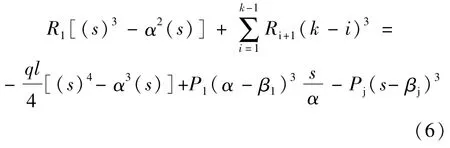
式中：k＝2，3，…，n－1，n－1＋α；s＝α＋k－1；βj＝bj／lj。

再補充力的平衡條件和力矩的平衡條件，可得矩陣方程：

求解矩陣方程可得各支座支反力，代入式（5）就可得到連續梁在荷載作用下的撓曲線方程表達式，從而求出每跨連續梁的向上撓度極值（各跨最大值）和向下撓度極值（各跨最小值）。

3 均布荷載下不同邊中跨跨徑比連續梁撓度

3．1 均布荷載下連續梁撓度特征

選取4～5跨連續梁在均布荷載作用時不同邊中跨跨徑比情況下的變形特征為對象，梁的撓曲變形采用無量綱化處理，表示為yEI／ql4，如圖2所示。當邊中跨跨徑比小于1時，為方便比較圖中邊跨按跨長為1繪制。

圖2 連續梁撓度特征曲線

由圖2可知，邊中跨跨徑比對第1～3跨撓度有明顯影響，當邊中跨跨徑小于0．8時，邊跨會出現向上的撓度，當邊中跨跨徑比大于等于0．8時，第2跨靠近支座處出現向上撓度，究其原因由于連續梁在支座處左右兩側剪力值不等所造成。較為合理的邊中跨跨徑比可使梁在均布荷載作用下各跨向下撓度極值趨于一致。對3～7跨連續梁在均布荷載作用下的分析表明，第3跨以后的撓度基本不隨邊中跨跨徑比的變化而變化。

3．2 邊中跨跨徑比對撓度極值的影響

選取4～5跨連續梁在均布荷載作用下各跨向上撓度極值和向下撓度極值為例，說明隨邊中跨跨徑比的變化情況，如圖3、圖4所示。

圖3中，當α小于等于0．81時，第1跨向上撓度極值隨α的增加呈先增加后減小趨勢，在α值為0．4時向上撓度極值最大。第2跨的向上撓度極值在α小于0．83時為零；當α大于0．83時，隨α的增加而增加。第3跨的向上撓度極值變化趨勢與第1跨相似，只是向上撓度極值遠小于第1跨，其余跨向上撓度極值基本趨于零。綜合各跨撓度情況，當α值在0．81～0．83時，連續梁向上撓度極值接近于零。

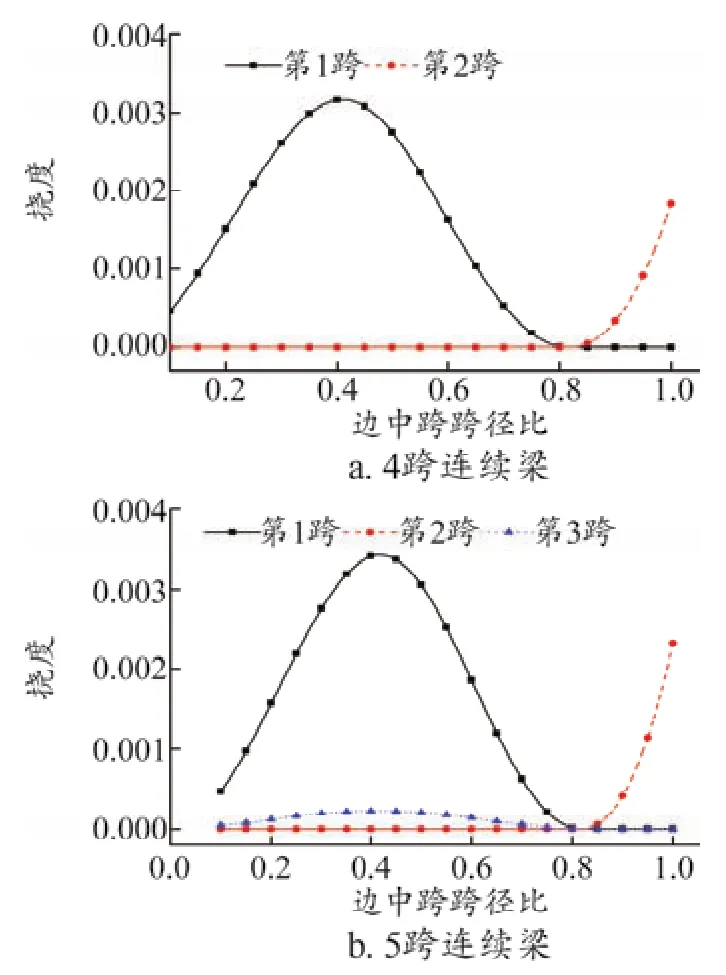
圖3 向上撓度極值隨邊中跨跨徑比變化曲線

圖4中，當α小于等于0．5時，第1跨向下撓度極值為零，當α大于0．5時，向下撓度極值隨著α的增加而增加。第2跨的向下撓度極值隨α的變化趨勢呈先增加后減小趨勢，在α值為0．4時，向下撓度極值最大。第3跨的向下撓度極值隨α的變化趨勢呈先減小后增加趨勢，在α值為0．4時，向下撓度極值最小。要各跨向下撓度極值均取較小值，應取圖4曲線交點處位置，此時α值為0．82。

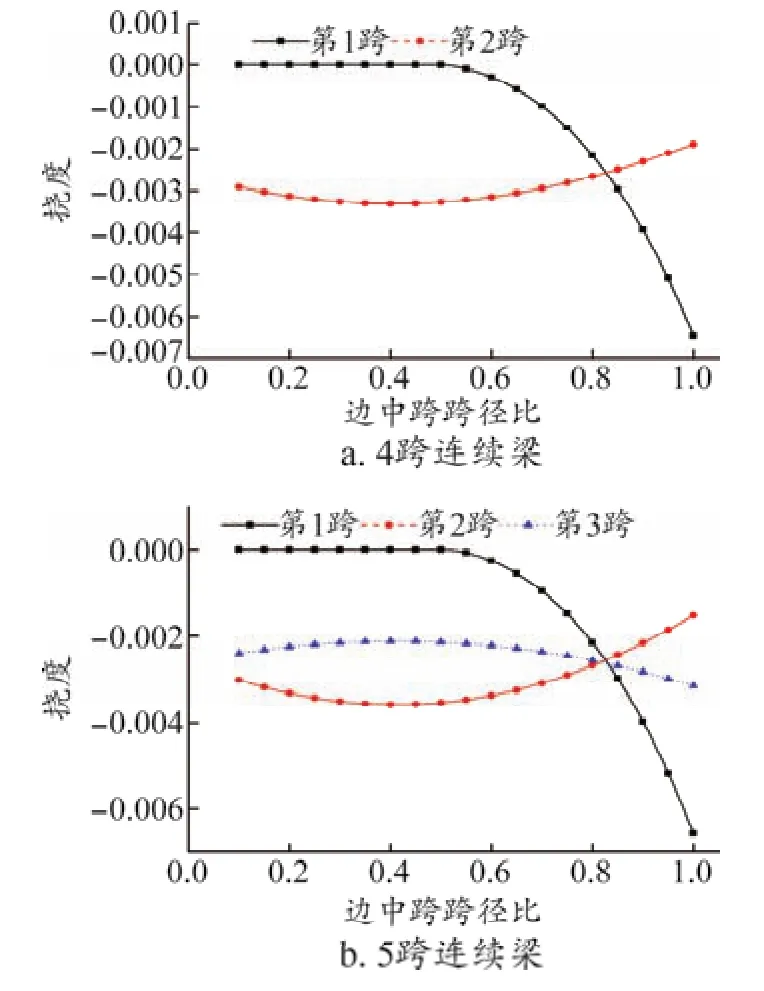
圖4 向下撓度極值隨邊中跨跨徑比變化曲線

3．3 跨數對連續梁撓度的影響

選取3～7跨連續梁向上撓度最大值和向下撓度最大值在不同邊中跨跨徑比下的計算結果，如圖5所示。

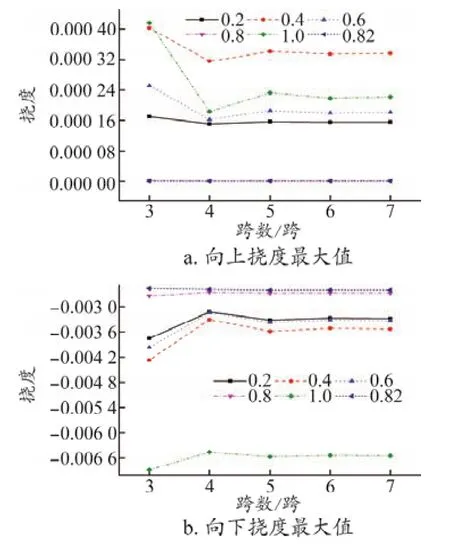
圖5 撓度隨跨數變化曲線

連續梁向上撓度最大值和向下撓度最大值隨跨數的增加呈波動變化關系，跨數越小波動幅度越大。當跨數大于5跨時，向上撓度最大值和向下撓度最大值基本趨于穩定值，只有邊中跨跨徑比α接近0．82時，向上撓度最大值和向下撓度最大值波動幅度最小，基本不隨跨數的增加而變化。

4 集中荷載下不同邊中跨跨徑比連續梁撓度

當有移動集中荷載（P＝1）作用在連續梁上時，位移也采用無量綱化表示，則集中荷載作用下的位移表示為yEI／Pl3，可用位移影響線表示移動荷載作用下連續梁某位置的變形[19]，將所有位置繪制的位移影響線曲線疊加，得到一個填充區域，這個區域的上、下邊界線就是結構的位移影響線包絡圖。位移影響線包絡圖反映了移動荷載在連續梁上作用時，所產生的最大和最小撓度。

4．1 集中荷載下連續梁撓度影響線包絡圖特征

以4～5跨連續梁為例，在集中荷載作用下不同邊中跨跨徑比的位移影響線包絡圖特征如圖6所示。當邊中跨跨徑比小于1時，為方便比較圖中邊跨按跨長為1繪制。邊中跨跨徑比的變化對第1跨和第2跨的撓度包絡圖極值影響最為明顯，第3跨及以后的影響可忽略不計。對3～7跨連續梁在集中荷載作用的分析結果表明，第3跨以后的撓度包絡圖極值基本不隨邊中跨跨徑比的變化而變化。

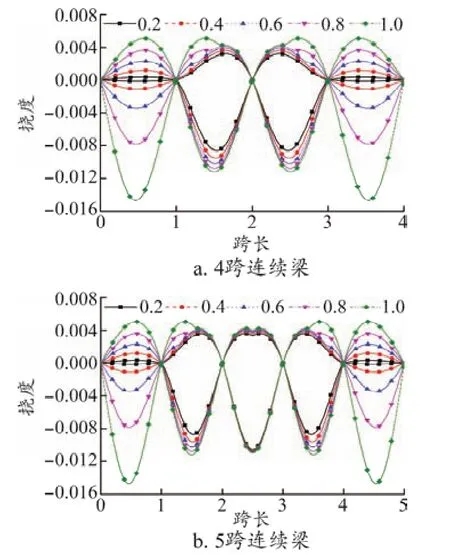
圖6 連續梁撓度影響線包絡圖

4．2 邊中跨跨徑比對撓度影響線極值的影響

分別將4～5跨連續梁前3跨的撓度影響線包絡圖極值在不同邊中跨跨徑比下的變化情況用圖7表示。可見無論向上撓度極值還是向下撓度極值都隨著邊中跨跨徑比的增加而增加，第1跨隨邊中跨跨徑比的增加變化幅度最為明顯，其他跨增幅逐漸趨于平緩。

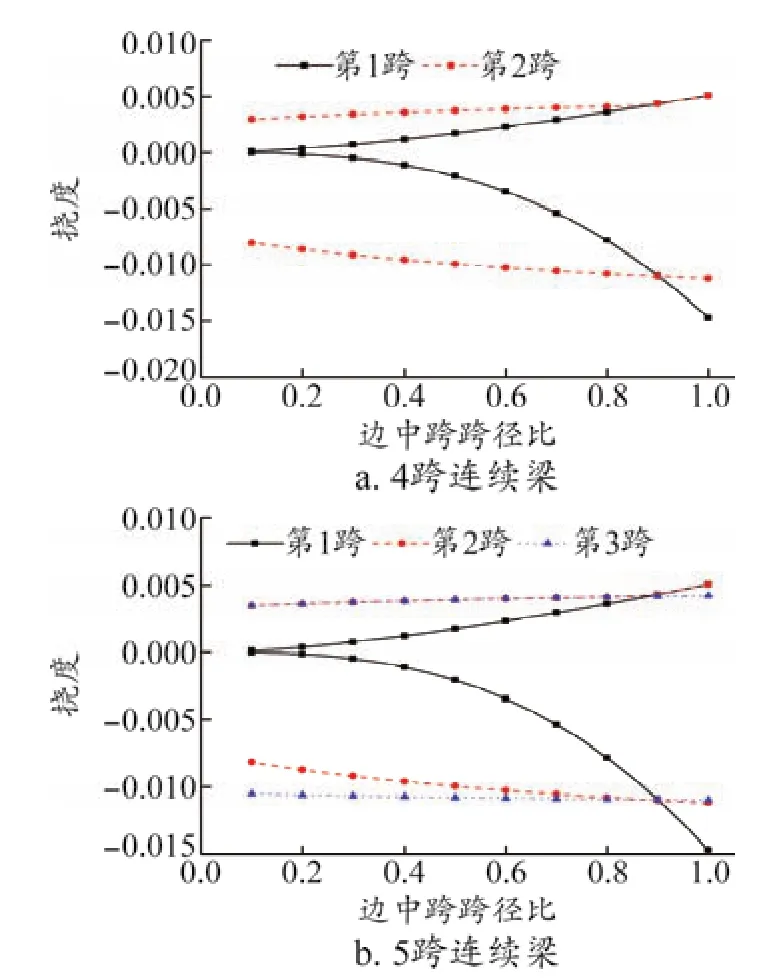
圖7 連續梁各跨撓度影響線包絡圖極值特征曲線

將3～7跨連續梁在集中荷載作用下位移影響線包絡圖的向上和向下最大值隨邊中跨跨徑比的變化情況用圖8表示。可見向上撓度影響線包絡圖和向下撓度影響線包絡圖的最大值隨α的增加而增加，向上撓度影響線包絡圖的最大值當α大于0．88后增幅更為明顯，而向下撓度影響線包絡圖的最大值當α大于0．9后增幅明顯。考慮到在集中荷載下連續梁撓度增幅不要過大，則應使邊中跨跨徑比小于等于0．88。

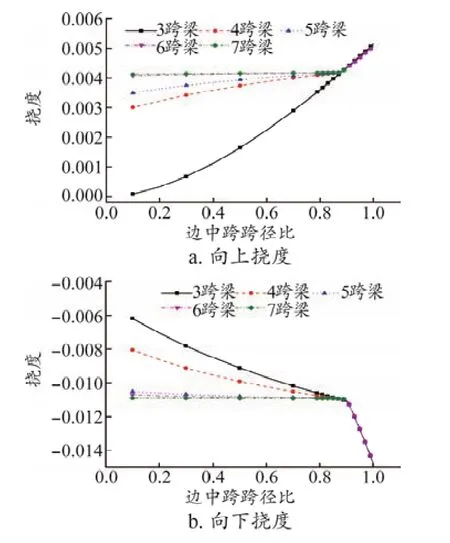
圖8 撓度影響線包絡圖最大值

4．3 跨數對連續梁撓度影響線極值的影響

選取3～7跨連續梁向上撓度影響線包絡圖最大值和向下撓度影響線包絡圖最大值在不同邊中跨跨徑比下的計算結果進行分析。

連續梁向上位移影響線包絡圖最大值和向下位移影響線包絡圖最大值隨跨數的增加基本呈逐漸增加的趨勢，當跨數大于7時位移影響線包絡圖最大值基本趨于恒定。當邊中跨跨徑比大于等于0.88時，向上位移影響線包絡圖最大值不隨跨數的增加而變化；當邊中跨跨徑比大于等于0.90時，向下位移影響線包絡圖最大值也不隨跨數的增加而變化。

5 結論

通過對不同跨數和不同邊中跨跨徑比情況下等截面連續梁的撓度分析，得出以下結論：

（1）均布荷載作用下，當邊中跨跨徑比接近0.82時，各跨向下撓度極值取較小值，各跨向上撓度值為零。

（2）均布荷載作用下，當邊中跨跨徑比接近0.82時，各跨撓度最大值基本不隨連續梁跨數的增加而變化。

（3）集中荷載作用下，當邊中跨跨徑比小于等于0.88時，各跨向上、向下撓度影響線包絡圖的最大值取值較為合理。

（4）綜合考慮均布荷載和集中荷載兩種作用情況，當邊中跨跨徑比為0.82時，連續梁撓度整體較小，撓度最大值基本不隨連續梁跨數的增加而變化。

雖然確定等截面連續梁橋的跨徑布置受地形地貌、跨越障礙等因素的限制，但對多跨布置的連續梁橋，當橋下凈空無要求時可采用邊跨和中跨不等跨布置。此時，為了使連續梁在荷載作用下撓曲變形總體最小，邊中跨跨徑比建議取值為0.82。