基于混合效應(yīng)模型的迪慶云冷杉林地上生物量遙感估測

盧騰飛，周 律，胡中岳，歐光龍，胥 輝

（西南林業(yè)大學(xué) 西南地區(qū)生物多樣性保育國家林業(yè)和草原局重點(diǎn)實(shí)驗(yàn)室，云南 昆明 650233）

森林生物量是森林生態(tài)系統(tǒng)的核心數(shù)據(jù)，也是森林碳匯研究的基礎(chǔ)[1]。傳統(tǒng)生物量獲取方法已經(jīng)不能滿足人們對大尺度生物量計(jì)算的需求。遙感技術(shù)的日益發(fā)展，極大提高了森林生物量大尺度估算、及時(shí)性掌控和實(shí)時(shí)性監(jiān)測的效率。由于Landsat影像不僅能夠容易免費(fèi)獲取，而且具有中等的空間分辨率和光譜分辨率以及能夠提供較長時(shí)間序列的歷史數(shù)據(jù)等優(yōu)點(diǎn)，被眾多學(xué)者[2]廣泛應(yīng)用于不同地區(qū)不同林分的生物量遙感估測中。基于光學(xué)遙感技術(shù)估測生物量存在的飽和現(xiàn)象已經(jīng)受到廣泛的關(guān)注[3]，再加之遙感模型的限制，如線性回歸模型普遍存在預(yù)估精度不高，模型泛化能力差，估測結(jié)果的殘差與生物量呈明顯的線性關(guān)系等問題[2]，往往會(huì)造成生物量估測的低值高估與高值低估問題，影響了遙感估測生物量精度。雖然一些學(xué)者[4?5]通過構(gòu)建人工神經(jīng)網(wǎng)絡(luò)模型和隨機(jī)森林等非參數(shù)機(jī)器學(xué)習(xí)模型提高了線性多變量模型的預(yù)估精度，但是由于其“黑箱”操作很難反映生物量與遙感參數(shù)之間的機(jī)制過程[6]，不具有推廣性。正是由于混合效應(yīng)模型包含了固定效應(yīng)和隨機(jī)效應(yīng)2個(gè)部分，可以同時(shí)分析組水平和個(gè)體水平數(shù)據(jù)，并且在處理不規(guī)則及不平衡的分層數(shù)據(jù)，以及在分析數(shù)據(jù)的相關(guān)性方面具有其他模型無法比擬的優(yōu)勢[7?8]而被廣泛使用。曾偉生等[9]利用線性混合效應(yīng)模型和啞變量模型方法建立了貴州省杉木Cunninghamialanceolata林和馬尾松Pinusmassoniana林地上生物量通用性模型。董利虎等[10]為了提高紅松Pinuskoraiensis人工林枝條生物量模型的精度采用了混合效應(yīng)模型，并與基礎(chǔ)模型的擬合效果進(jìn)行檢驗(yàn)對比。胥喆等[11]采用非線性混合效應(yīng)模型，選擇區(qū)域作為隨機(jī)效應(yīng)，建立了高山松Pinusdensata林生物量估測模型。他們的研究都表明：混合模型各項(xiàng)指標(biāo)優(yōu)于一般多變量模型，能有效地提高模型的預(yù)估精度。云杉Piceakoraiensis和冷杉Abiesholophylla均為高海拔地區(qū)特有樹種，尤其在云南省迪慶藏族自治州廣泛分布，占全州森林面積的33.23%[12]。其中云杉為中國西部高山地區(qū)特有樹種，稍耐陰，耐寒，耐旱，而冷杉常形成純林，或與性喜冷濕的云杉組成針葉混交林，形成云冷杉林。小班是森林資源清查和經(jīng)營利用的基本單位，以小班開展研究調(diào)查，可以快速、有效、客觀地對森林資源變化進(jìn)行遙感監(jiān)測，滿足時(shí)效性與準(zhǔn)確性等要求[13]。MOZGERIS[14]和FERNáNDEZ-MANSO 等[15]的研究均表明：以小班為單位的生物量估算可以提高其精準(zhǔn)度。郎曉雪等[16]利用角控樣地?cái)?shù)據(jù)建立云冷杉林蓄積量遙感估測模型的結(jié)果值與傳統(tǒng)森林資源二類調(diào)查數(shù)據(jù)結(jié)果誤差僅為1.14%。鑒于此，本研究將基于森林資源二類調(diào)查數(shù)據(jù)結(jié)合同時(shí)期的Landsat 8 OLI遙感影像，構(gòu)建不同遙感估測模型，實(shí)現(xiàn)對高海拔、大尺度云冷杉林生物量的精確估算，減小生物量遙感估測中低值高估與高值低估的影響，為森林資源二類調(diào)查數(shù)據(jù)廣泛利用提供參考和借鑒意義，同時(shí)為迪慶區(qū)域碳匯效益的準(zhǔn)確估算、森林生態(tài)保護(hù)和科學(xué)經(jīng)營提供規(guī)劃與指導(dǎo)依據(jù)。

1 研究區(qū)概況

研究區(qū)云南省迪慶藏族自治州，地處 26°52′10″～29°15′09″N，98°35′38″～100°18′22″E，屬于寒溫帶氣候，平均海拔3 380 m，年平均氣溫為4.7～16.5 ℃。全州林業(yè)用地173.96 萬hm2，森林覆蓋率高達(dá)73.9%，境內(nèi)主要樹種有云杉、冷杉、云南松Pinusyunnanensis、高山松等，是云南省重點(diǎn)林區(qū)，森林資源極為豐富，其中云冷杉林面積57.82 萬hm2[12]。

2 材料與方法

2.1 數(shù)據(jù)來源

地面數(shù)據(jù)。地面數(shù)據(jù)為云南省迪慶藏族自治州2016年完成的森林資源二類調(diào)查數(shù)據(jù)，包括小班空間位置、面積、起源、優(yōu)勢樹種、蓄積量、齡組等基本小班調(diào)查因子。

遙感影像數(shù)據(jù)。由于該地二類調(diào)查數(shù)據(jù)調(diào)查時(shí)間大多在冬春季，本研究選取與地面數(shù)據(jù)同時(shí)期的空間分辨率為30 m的Landsat 8 OLI遙感影像。數(shù)據(jù)(表1)來源于中國科學(xué)院計(jì)算機(jī)網(wǎng)絡(luò)信息中心地理空間數(shù)據(jù)云平臺(http://www.gscloud.cn)。

表 1 研究區(qū) Landsat 8 OLI 影像基本信息Table 1 Basic information of Landsat 8 OLI images in study area

數(shù)字高程 (DEM)數(shù)據(jù)與輔助數(shù)據(jù)。迪慶藏族自治州DEM數(shù)據(jù)分辨率為30 m。本研究采用的輔助數(shù)據(jù)為迪慶藏族自治州行政區(qū)劃矢量圖，用來裁剪最終影像。

2.2 研究方法

2.2.1 地面數(shù)據(jù)計(jì)算 地面生物量數(shù)據(jù)通過生物量—蓄積量轉(zhuǎn)換來計(jì)算。參考胥輝等[12]的云南省迪慶地區(qū)云冷杉喬木層生物量—蓄積量轉(zhuǎn)換因子(表2)。

表 2 云冷杉蓄積量—生物量轉(zhuǎn)換因子信息指數(shù)Table 2 Spruce and fir storage—biomass conversion factor information index

2.2.2 小班樣本數(shù)據(jù)確定 首先，從二類調(diào)查數(shù)據(jù)里提取優(yōu)勢樹種為云冷杉的小班班塊，刪除蓄積量為0的異常小班數(shù)據(jù)，再利用ARCGIS 10.5軟件的“采樣—?jiǎng)?chuàng)建隨機(jī)點(diǎn)”工具，設(shè)置約束范圍1.5 km[17]，結(jié)果為1 233塊。最后進(jìn)行目視檢查，確保云冷杉小班不含其他非植被像元。最終留得1 228塊小班樣本數(shù)據(jù)，其中983塊小班(80%)用于建模(訓(xùn)練)，245塊小班(20%)用于獨(dú)立性檢驗(yàn)(表3)。

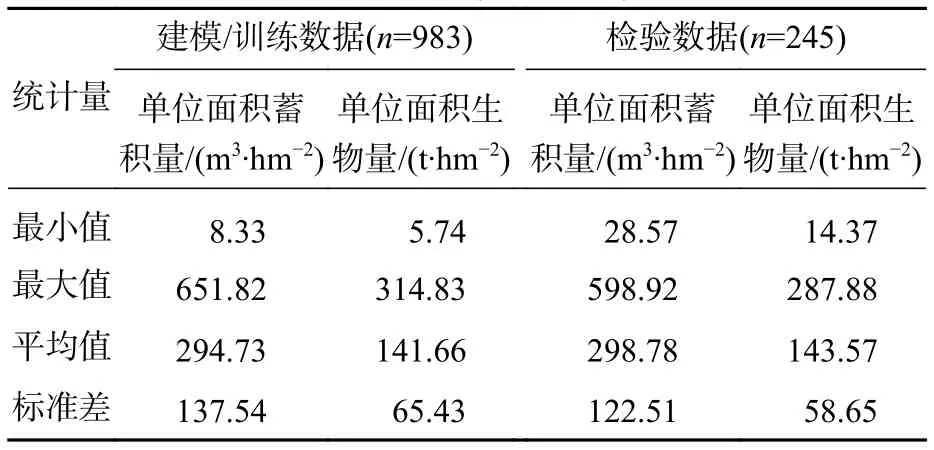
表 3 建模及檢驗(yàn)數(shù)據(jù)基本情況Table 3 Modeling and testing data

2.2.3 遙感影像預(yù)處理及遙感因子的提取 本研究采用的遙感數(shù)據(jù)為 Landsat 8 OLI Leve1 級別。數(shù)據(jù)已進(jìn)行幾何粗校正，精度滿足研究需求，并對遙感數(shù)據(jù)進(jìn)行輻射定標(biāo)、FLAASH大氣校正，消除傳感器本身、大氣、太陽高度角等帶來的干擾，得到真實(shí)反射率數(shù)據(jù)。然后為消除地表陰影對遙感特征值的影響，本研究采用1∶50 000地形圖生成的30 m空間分辨率數(shù)字高程圖進(jìn)行地形校正，其具體流程方法參照董宇[18]的研究。同時(shí)，根據(jù)現(xiàn)有迪慶藏族自治州云冷杉林小班矢量邊界對遙感影像進(jìn)行棋盤分割與融合，從而保證2種數(shù)據(jù)在空間尺度的匹配，最后對影像進(jìn)行鑲嵌和裁剪處理。

遙感因子的提取大致分為4類，包括原始單波段因子、植被指數(shù)[19]、歸一化植被指數(shù)[20]、信息增強(qiáng)因子[19?20](表 4)。

表 4 建模變量因子Table 4 Modeling variable factors

以云冷杉各個(gè)小班面狀數(shù)據(jù)為單位，利用ARCGIS 10.5軟件的“分區(qū)統(tǒng)計(jì)”功能，統(tǒng)計(jì)每個(gè)小班樣地內(nèi)各個(gè)遙感因子反射率的最小值(以下稱MIN)、最大值(MAX)和平均值(MEAN)。然后進(jìn)行因子優(yōu)選，選取與生物量相關(guān)性極顯著且因子之間相關(guān)性小的因子參與到模型的構(gòu)建中。本研究采用的是皮爾遜相關(guān)性檢驗(yàn)，采用方差膨脹因子(VIF大于10)解決因子之間的多重共線性問題。

2.2.4 云冷杉林生物量飽和值確定方法 本研究通過構(gòu)建生物量與波段反射率間的散點(diǎn)圖，用曲線擬合兩者之間的函數(shù)關(guān)系，計(jì)算函數(shù)所對應(yīng)的極值即為生物量遙感估測的數(shù)據(jù)飽和值。

2.2.5 生物量遙感估測模型的構(gòu)建 ①逐步線性回歸模型的構(gòu)建。利用SPSS 23軟件進(jìn)行線性逐步回歸模型的擬合，分別構(gòu)建生物量與各個(gè)遙感因子反射率最小值、最大值和平均值的逐步回歸模型，通過偏F統(tǒng)計(jì)檢驗(yàn)，將自變量一個(gè)個(gè)引入到模型中；同時(shí)，每引進(jìn)一個(gè)新變量，將對已納入的變量再次進(jìn)行檢驗(yàn)，確保模型中只包含對因變量影響最顯著的自變量的最優(yōu)模型[21]。其基本表達(dá)式為：

式(1)中：y為生物量因變量；b0為常數(shù)項(xiàng)；b1，b2，···，bn為擬合參數(shù)；x1，x2，···，xn為自變量；n為自變量個(gè)數(shù)；ε為隨機(jī)殘差。②BP神經(jīng)網(wǎng)絡(luò)模型的構(gòu)建。本研究在Matlab軟件中采用3層BP神經(jīng)網(wǎng)絡(luò)，完成模型構(gòu)建、模型估測及預(yù)測值的計(jì)算。輸入層的神經(jīng)元個(gè)數(shù)為回歸模型最終優(yōu)選的自變量，輸出層神經(jīng)元個(gè)數(shù)為1，隱含層神經(jīng)元個(gè)數(shù)參考經(jīng)驗(yàn)公式(2)選取。網(wǎng)絡(luò)訓(xùn)練函數(shù)采用trainlm，網(wǎng)絡(luò)最大訓(xùn)練次數(shù)為1 000，學(xué)習(xí)速率為0.01，目標(biāo)誤差選取0.001、0.005、0.010與隱含層神經(jīng)元個(gè)數(shù)進(jìn)行組合訓(xùn)練網(wǎng)絡(luò)。

式中(2)：m為隱含層神經(jīng)元個(gè)數(shù)；n為輸入層神經(jīng)元個(gè)數(shù)；l為輸出層神經(jīng)元個(gè)數(shù)；a為1～10的整數(shù)。③混合效應(yīng)模型的構(gòu)建。利用R語言的nlme模塊實(shí)現(xiàn)混合效應(yīng)模型的構(gòu)建。研究發(fā)現(xiàn)：迪慶藏族自治州垂直氣候特點(diǎn)顯著，在不同區(qū)域內(nèi)森林生物量生長存在隨機(jī)差異。按迪慶藏族自治州行政區(qū)劃的各個(gè)縣(市)，分為不同區(qū)域，設(shè)為第1水平隨機(jī)效應(yīng)因子；在不同區(qū)域內(nèi)又嵌套著不同齡組的云冷杉林，設(shè)為第2水平隨機(jī)效應(yīng)因子，故本研究基于回歸模型為基礎(chǔ)模型，考慮單水平(區(qū)域、齡組)和嵌套兩水平(區(qū)域+齡組)分別構(gòu)建云冷杉林生物量線性混合效應(yīng)模型。其基本形式如下：

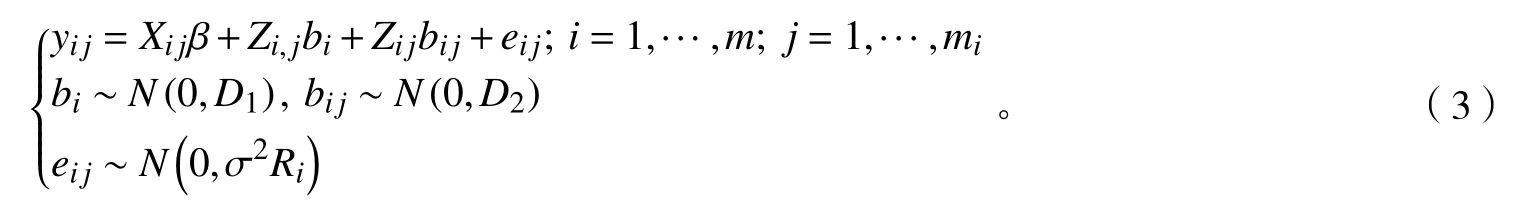
式(3)中：yij為第i個(gè)1水平中的第j個(gè)2水平內(nèi)的觀察值；m為第1水平的分組數(shù)；mi為對應(yīng)于第1水平的第2水平的分組數(shù)；Xij為已知設(shè)計(jì)矩陣。在本研究中即為最優(yōu)逐步回歸模型；β為固定參數(shù)向量；Zi,j和Zij分別為1水平和2水平的隨機(jī)效應(yīng)設(shè)計(jì)矩陣；bi和bij分別為1水平和2水平的隨機(jī)參數(shù)向量；D1和D2分別為1水平和2水平的組間方差-協(xié)方差矩陣；σ2為方差；Ri為模型的組內(nèi)方差-協(xié)方差結(jié)構(gòu)；eij為模型的誤差項(xiàng)。

根據(jù)眾多學(xué)者的研究[8,10,22?23]，完成混合效應(yīng)模型的構(gòu)建還需要以下內(nèi)容。①確定參數(shù)效應(yīng)：本研究將不同隨機(jī)參數(shù)組合的混合模型進(jìn)行擬合，通過評價(jià)模型擬合指標(biāo)，即比較Akaike信息指數(shù)(AIC)、貝葉斯信息指數(shù)(BIC)和對數(shù)似然值(logLik)參數(shù)指標(biāo)，其中AIC、BIC越小越好，logLik越大越好。②確定組間方差-協(xié)方差結(jié)構(gòu)(D矩陣)：當(dāng)隨機(jī)效應(yīng)參數(shù)的個(gè)數(shù)大于1時(shí)應(yīng)考慮組間方差-協(xié)方差結(jié)構(gòu)。本研究將比較廣義正定矩陣(UN)、復(fù)合對稱結(jié)構(gòu)(CS)和對角矩陣結(jié)構(gòu)(UN1)3種結(jié)構(gòu)對模型的影響。具體形式(以2個(gè)隨機(jī)效應(yīng)參數(shù)為例)如下：

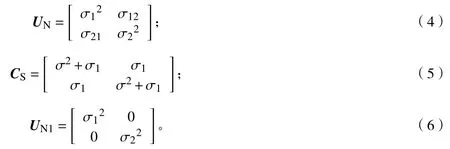
③確定組內(nèi)方差-協(xié)方差結(jié)構(gòu)(R矩陣)：首先要考慮組內(nèi)誤差的異方差性和自相關(guān)性問題。為了解決這2個(gè)方面問題從而確定組內(nèi)方差-協(xié)方差結(jié)構(gòu)，林業(yè)上主要采用式(7)進(jìn)行描述：

式(7)中：Ri為組內(nèi)方差-協(xié)方差矩陣；σi2為混合模型的誤差方差值；Ψi0.5為描述方差異質(zhì)性的對角矩陣；Γi(θ)為組內(nèi)誤差自相關(guān)結(jié)構(gòu)矩陣。

本研究將通過殘差分布圖來判斷誤差的異質(zhì)性。由于本研究所使用的數(shù)據(jù)不涉及時(shí)間序列相關(guān)性，故主要測試指數(shù)函數(shù)(exponential)、高斯函數(shù)(Gaussian)和球面函數(shù)(spherical)3種空間自相關(guān)函數(shù)對模型的影響。具體結(jié)構(gòu)形式見文獻(xiàn)[24]。④混合效應(yīng)模型參數(shù)估計(jì)：在應(yīng)用混合效應(yīng)模型時(shí)，需要估計(jì)隨機(jī)參數(shù)。在本研究中，隨機(jī)效應(yīng)參數(shù)值可通過建模及檢驗(yàn)小班樣本數(shù)據(jù)已知信息，參考VONESH等[25]研究，利用最好線性無偏估計(jì)以及限制性極大似然法預(yù)測。具體形式如下：

式(9)中：yi為觀測值；i為預(yù)測值；n為樣本容量。

3 結(jié)果與分析

3.1 生物量與遙感因子相關(guān)性分析

利用本研究選取的41個(gè)遙感因子與樣本云冷杉林地上生物量進(jìn)行Pearson’s相關(guān)性分析，結(jié)果(表5)可以看出：相較于最大值和最小值反射率平均值與生物量之間相關(guān)性更強(qiáng)，其中B6波段的反射率平均值與生物量有最強(qiáng)的相關(guān)性，因此，基于B6波段分析和確定云冷杉林的生物量飽和值。

表 5 生物量與遙感因子各統(tǒng)計(jì)值相關(guān)性Table 5 Significant Pearson correlation coefficients between remote sensing factors and AGB

3.2 生物量飽和值的確定

基于B6波段遙感因子，選取常用含極值函數(shù)與生物量進(jìn)行曲線擬合求解云冷杉林地上生物量飽和值。由表6可知：冪函數(shù)擬合時(shí)有最高的決定系數(shù)R2(0.590)，故以其所對應(yīng)的冪函數(shù)極值(圖1)作為該波段的云冷杉林生物量飽和值，其值為233 t·hm?2。

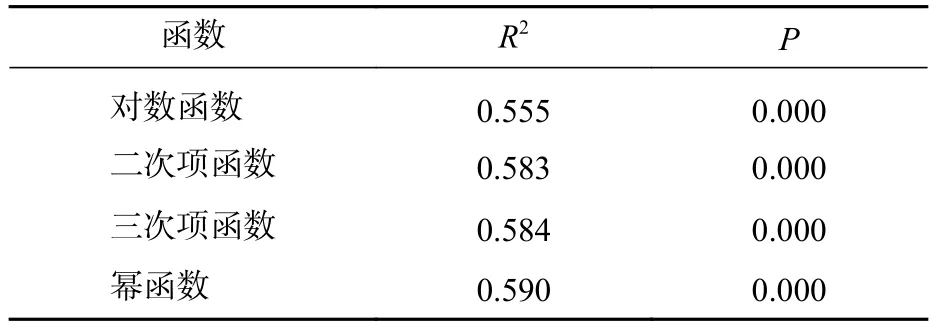
表 6 基于不同曲線擬合飽和值結(jié)果Table 6 Results of fitting saturation values based on different curves

圖 1 冪函數(shù)擬合云冷杉林生物量飽和曲線Figure 1 Power function fitting curve of spruce-fir forest biomass saturation

3.3 逐步線性回歸模型構(gòu)建結(jié)果

通過生物量與各個(gè)遙感因子反射率統(tǒng)計(jì)值構(gòu)建的逐步回歸模型結(jié)果可知，反射率平均值與生物量的回歸模型相較于采用最小值和最大值所構(gòu)建模型的Ra2最高，總相對誤差(13.715)和平均相對誤差(1.931)也均最優(yōu)。因此，采用反射率平均值與生物量所構(gòu)建的逐步回歸模型[式(10)]作為BP神經(jīng)網(wǎng)絡(luò)輸入層神經(jīng)元個(gè)數(shù)的納入依據(jù)以及混合效應(yīng)模型構(gòu)建的基礎(chǔ)模型。

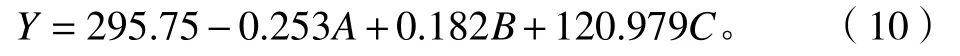
式(10)中：Y為因變量；A為B6波段值；B為B7波段值；C為歸一化植被指數(shù)(NDVI)。

3.4 BP 神經(jīng)網(wǎng)絡(luò)模型構(gòu)建結(jié)果

經(jīng)上節(jié)回歸模型篩選出的自變量為3個(gè)，則經(jīng)計(jì)算隱含層神經(jīng)元個(gè)數(shù)的取值范圍為[3, 12]的整數(shù)。通過對隱含層神經(jīng)元個(gè)數(shù)及目標(biāo)誤差的每個(gè)不同組合進(jìn)行10次訓(xùn)練，取平均值。最終隱含層神經(jīng)元個(gè)數(shù)與目標(biāo)誤差組合為(6, 0.01)時(shí)，Ra2最優(yōu)(0.542)，總相對誤差最小(12.190)。

3.5 混合效應(yīng)模型構(gòu)建結(jié)果

3.5.1 單水平混合效應(yīng)模型 確定參數(shù)效應(yīng)和組間方差-協(xié)方差結(jié)構(gòu)需要同時(shí)進(jìn)行。首先將組間方差-協(xié)方差結(jié)構(gòu)設(shè)為默認(rèn)廣義正定結(jié)構(gòu)，擬合結(jié)果見表7。基于區(qū)域效應(yīng)水平，共有7種擬合模型，其中有6種模型收斂，混合效應(yīng)模型相較于基礎(chǔ)模型其AIC和BIC值均較小，logLik值均較大，表現(xiàn)出混合效應(yīng)模型比基本模型有更好的擬合精度，其中模型1有最小的AIC、BIC值和最大的logLik值，即把a(bǔ)1考慮為隨機(jī)參數(shù)的混合模型作為基于區(qū)域效應(yīng)水平的最優(yōu)模型。基于齡組效應(yīng)水平，共有7種擬合模型，均收斂，結(jié)果見表7。混合模型同樣相較于基礎(chǔ)模型有著較優(yōu)的擬合指標(biāo)，其中模型1有最小的AIC、BIC值和最大的logLik值，即將a1考慮為隨機(jī)參數(shù)的混合模型作為基于齡組效應(yīng)水平的最優(yōu)模型。

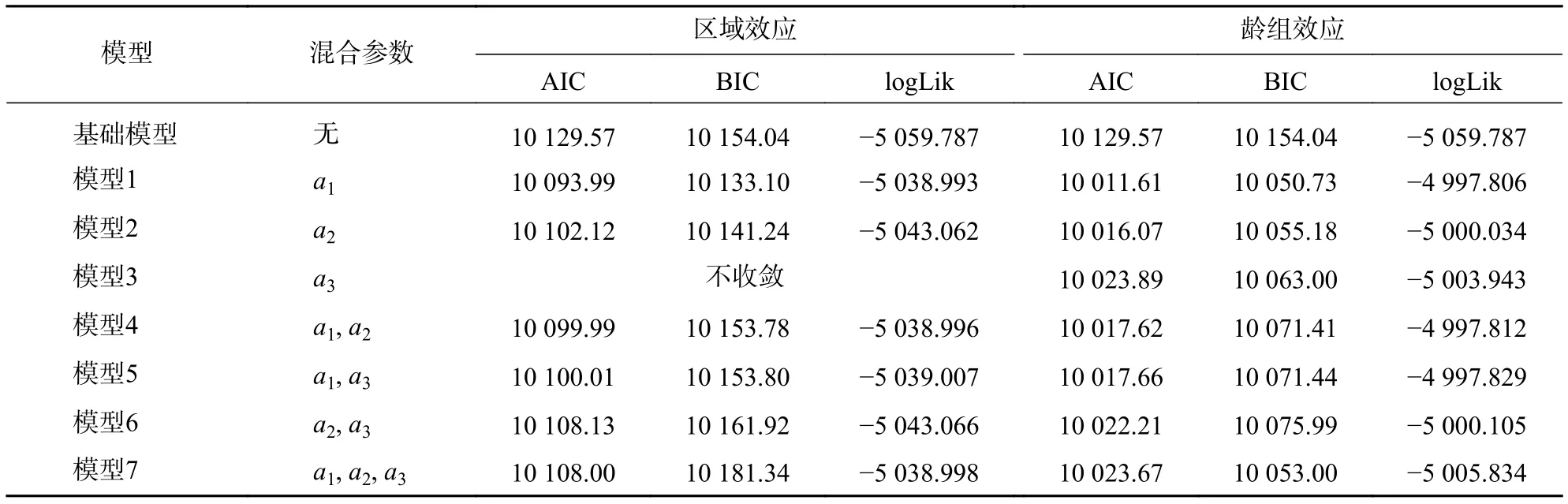
表 7 基于單水平混合參數(shù)選擇擬合結(jié)果Table 7 Selection of fitting results based on single-level mixing parameters

3.5.2 兩水平混合效應(yīng)模型 兩水平混合效應(yīng)模型將同時(shí)考慮區(qū)域效應(yīng)和齡組效應(yīng)。當(dāng)模型有2個(gè)隨機(jī)參數(shù)時(shí)，得到9種擬合模型，其中有7種模型收斂；當(dāng)模型有3個(gè)隨機(jī)參數(shù)時(shí)，共有18種擬合模型，其中有14種模型收斂；當(dāng)模型有4個(gè)隨機(jī)參數(shù)時(shí)，共有15種擬合模型，其中有9種模型收斂；當(dāng)模型有5個(gè)隨機(jī)參數(shù)時(shí)，共有6種擬合模型，其中有3種模型收斂；當(dāng)模型有6個(gè)隨機(jī)參數(shù)時(shí)，只有1種擬合模型且收斂。由于擬合模型眾多，本研究只列出相同隨機(jī)參數(shù)下的最優(yōu)混合模型，結(jié)果見表8。綜合分析模型的3個(gè)擬合指標(biāo)，將模型1，即把區(qū)域效應(yīng)含有隨機(jī)參數(shù)a1和齡組效應(yīng)含有隨機(jī)參數(shù)a1的混合模型作為兩水平效應(yīng)上的最優(yōu)模型。然后又將林業(yè)上使用較為廣泛的2種組間方差-協(xié)方差結(jié)構(gòu)納入模型，結(jié)果見表9。通過對AIC、BIC、logLik值和似然比檢驗(yàn)結(jié)果可見，廣義正定結(jié)構(gòu)表現(xiàn)較優(yōu)，因此將兩水平混合效應(yīng)模型的組間方差-協(xié)方差結(jié)構(gòu)設(shè)為廣義正定結(jié)構(gòu)。

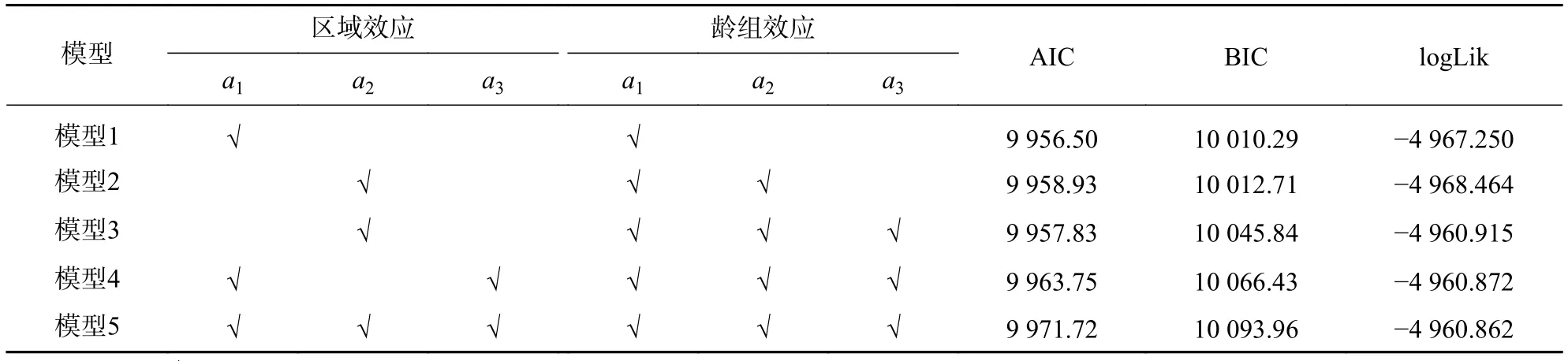
表 8 基于兩水平混合參數(shù)選擇擬合結(jié)果Table 8 Selection of fitting results based on two levels of mixing parameters

表 9 基于隨機(jī)參數(shù)不同組間方差-協(xié)方差結(jié)構(gòu)混合模型擬合結(jié)果Table 9 Mixed model fitting results of variance-covariance structure between groups based on random parameters

3.5.3 誤差的異方差性和自相關(guān)性 確定組內(nèi)方差-協(xié)方差結(jié)構(gòu)。首先，要確定誤差的異方差性和自相關(guān)性。本研究將通過殘差分布圖來判斷誤差的異方差性，結(jié)果見圖2。與基本模型的殘差分布圖(圖2A)相比，各個(gè)水平的混合效應(yīng)模型的殘差分布圖(圖2B為區(qū)域效應(yīng)混合模型預(yù)估殘差分布；圖2C為齡組效應(yīng)混合模型預(yù)估殘差分布；圖2D為兩水平混合效應(yīng)模型預(yù)估殘差分布)變化不明顯，分布范圍均表現(xiàn)為聚集0周圍的均勻分布，沒有顯示極不規(guī)則形狀(如拋物線狀、喇叭狀)，因此異方差的影響不在本研究的考慮中。然后又將指數(shù)函數(shù)、高斯函數(shù)和球面函數(shù)形式引入到各個(gè)效應(yīng)水平最優(yōu)混合模型中，結(jié)果如表10顯示。在區(qū)域效應(yīng)水平上將指數(shù)函數(shù)和高斯函數(shù)形式加入混合模型中并不能提高模型的擬合精度，似然比檢驗(yàn)也沒有顯著不同，而球面函數(shù)形式的AIC和logLik雖然優(yōu)于原模型，但似然比檢驗(yàn)并不顯著，因此在區(qū)域效應(yīng)水平上的混合模型不考慮組內(nèi)協(xié)方差結(jié)構(gòu)。在齡組效應(yīng)水平上當(dāng)考慮該3種協(xié)方差結(jié)構(gòu)時(shí)均能提高原模型擬合精度，其中指數(shù)函數(shù)形式的擬合精度最優(yōu)，似然比檢驗(yàn)顯著不同，因此基于齡組效應(yīng)水平的混合模型以考慮指數(shù)函數(shù)協(xié)方差結(jié)構(gòu)的模型。在兩水平上，當(dāng)考慮指數(shù)函數(shù)和 球面函數(shù)形式時(shí)，其AIC和logLik優(yōu)于原模型，但BIC不及原模型，似然比檢驗(yàn)也不顯著；考慮高斯函數(shù)形式時(shí)，其AIC和BIC不及原模型，logLik優(yōu)于原模型，似然比檢驗(yàn)不顯著。綜合分析后同樣在兩水平上的混合效應(yīng)模型也不考慮組內(nèi)協(xié)方差結(jié)構(gòu)。

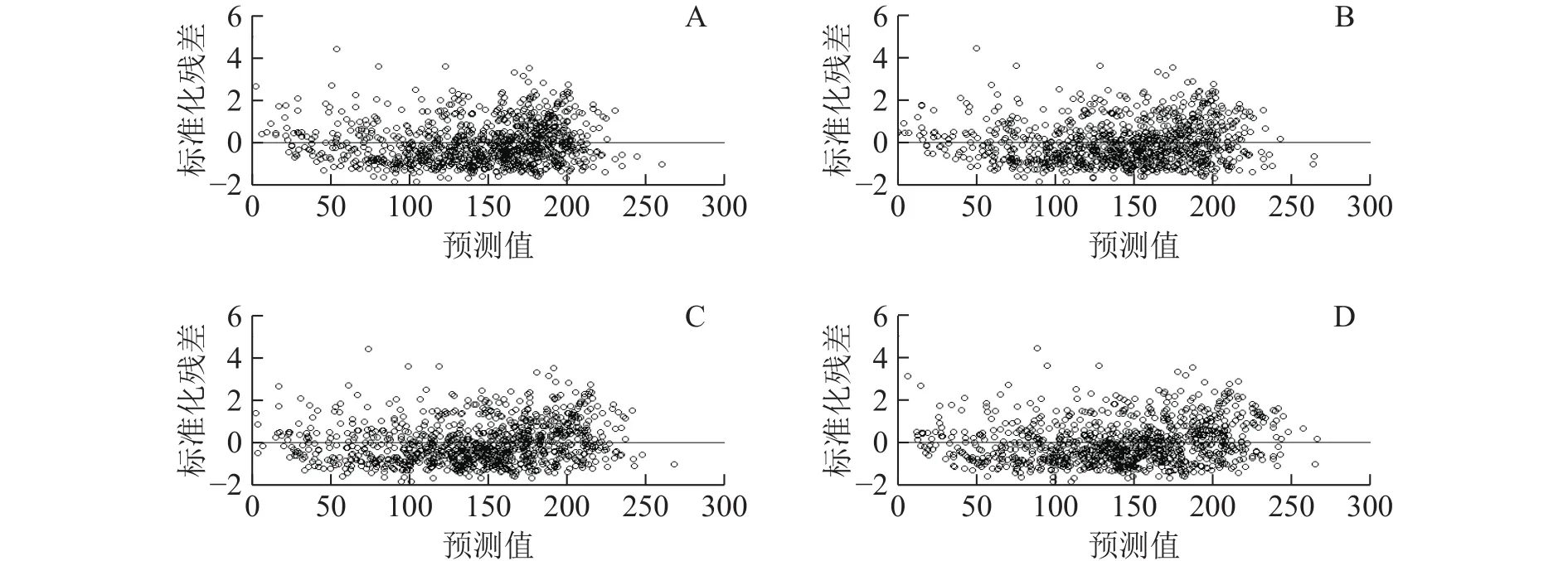
圖 2 基于回歸模型和混合效應(yīng)模型生物量估測殘差分布Figure 2 Biomass estimation residual distribution based on regression model and mixed effect model

表 10 考慮組內(nèi)協(xié)方差結(jié)構(gòu)矩陣后各個(gè)效應(yīng)混合模型比較結(jié)果Table 10 Comparison results of mixed effects models considering intra-group covariance matrix

通過以上步驟，確定了各水平最佳混合參數(shù)、組間矩陣結(jié)構(gòu)和自相關(guān)矩陣結(jié)構(gòu)后，把這幾個(gè)方面綜合考慮進(jìn)行模擬，確定了各個(gè)效應(yīng)混合模型形式。①區(qū)域效應(yīng)混合模型：

②齡組效應(yīng)混合模型：

③兩水平混合效應(yīng)模型：

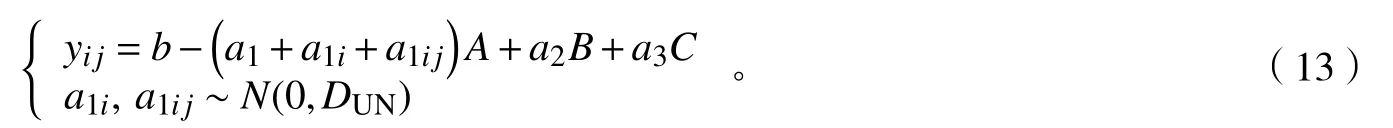
式(11)～(13)中：i為區(qū)域編號；j為齡組編號；a和b為常量；yij為i區(qū)域中j齡組云冷杉單位生物量預(yù)測值；A為B6波段值；B為B7波段值；C為NDVI值；a1、a2、a3分別為固定效應(yīng)擬合參數(shù)；a1i、a1ij分別為區(qū)域效應(yīng)和齡組效應(yīng)隨機(jī)參數(shù)；eij為模型誤差項(xiàng)；DUN為兩水平組間方差-協(xié)方差矩陣；Ri為組內(nèi)方差-協(xié)方差結(jié)構(gòu)；為未知樣地i的殘差方差； Γi(θ)為齡組效應(yīng)水平組內(nèi)誤差自相關(guān)結(jié)構(gòu)矩陣；xi為自變量。

3.5.4 混合模型獨(dú)立性檢驗(yàn) 綜合分析以上混合模型的擬合指標(biāo)，得出各個(gè)效應(yīng)水平上最優(yōu)混合效應(yīng)模型，其具體參數(shù)擬合結(jié)果如表11所示。結(jié)果表明：各個(gè)效應(yīng)水平上的混合模型相較于回歸模型均提高了其擬合精度。兩水平混合效應(yīng)模型的擬合指標(biāo)優(yōu)于單水平混合效應(yīng)模型，而在單水平混合模型中，齡組效應(yīng)混合模型的擬合指標(biāo)優(yōu)于區(qū)域效應(yīng)混合模型。從模型的獨(dú)立性檢驗(yàn)結(jié)果上看(表11)，各個(gè)效應(yīng)水平上混合模型的總相對誤差和平均相對誤差均優(yōu)于回歸模型，而齡組效應(yīng)混合模型有著最優(yōu)的總相對誤差和平均相對誤差。

表 11 生物量混合效應(yīng)模型擬合參數(shù)及獨(dú)立性檢驗(yàn)結(jié)果Table 11 Biomass mixed effect model fitting parameters and independence test results

3.6 模型評價(jià)及分段殘差檢驗(yàn)

由生物量分段殘差檢驗(yàn)結(jié)果(表12)可知：5種模型對云冷杉林生物量段的預(yù)估能力不同。總體來說，混合效應(yīng)模型的預(yù)估能力優(yōu)于回歸模型和BP神經(jīng)網(wǎng)絡(luò)模型，5種模型均在150～200 t·hm?2生物量段預(yù)估能力最優(yōu)，其絕對平均殘差最小。在低生物量段(＜100 t·hm?2)，5種模型均出現(xiàn)了低值高估現(xiàn)象，但其兩水平混合效應(yīng)模型表現(xiàn)較優(yōu)。在高生物量段(＞233 t·hm?2)，由于生物量值在生物量飽和閾值之上，5種模型均出現(xiàn)了嚴(yán)重的高值低估現(xiàn)象，但BP神經(jīng)網(wǎng)絡(luò)模型預(yù)估能力優(yōu)于回歸模型，而各效應(yīng)水平混合模型均顯著改善了高值低估，其平均殘差由回歸模型的79.39 t·hm?2、BP神經(jīng)網(wǎng)絡(luò)模型的72.37 t·hm?2降為區(qū)域效應(yīng)混合模型的 70.69 t·hm?2，齡組效應(yīng)混合模型的 68.65 t·hm?2，兩水平混合效應(yīng)模型的 55.43 t·hm?2。

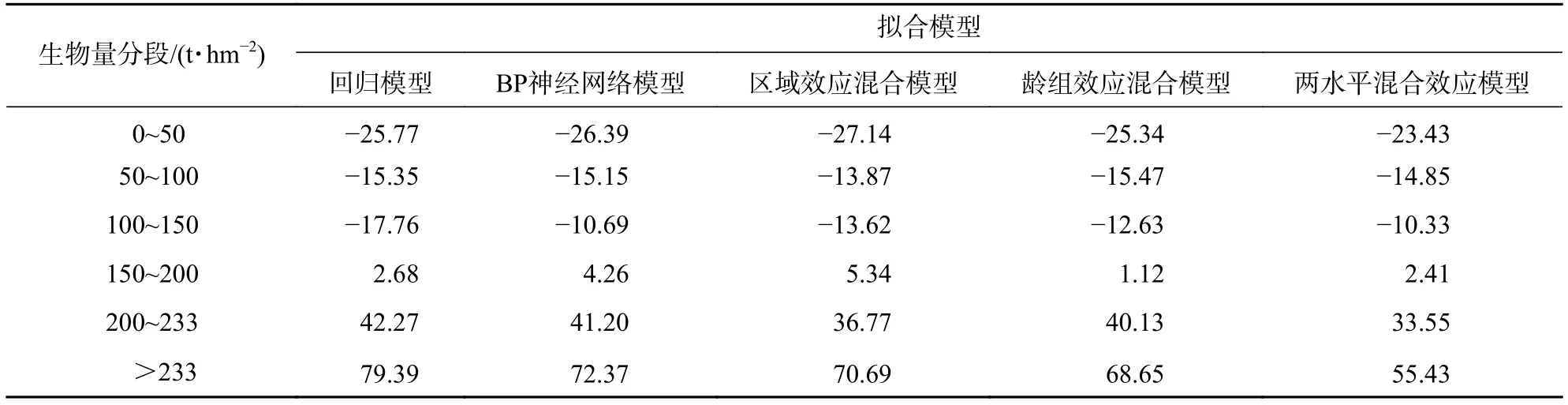
表 12 生物量分段殘差檢驗(yàn)Table 12 Biomass segmentation residual test

3.7 迪慶藏族自治州云冷杉林生物量估算

依據(jù)森林資源二類調(diào)查數(shù)據(jù)獲取迪慶藏族自治州云冷杉林空間分布位置，基于Landsat 8 OLI影像，采用像元法，利用所構(gòu)建模型計(jì)算每個(gè)小班像元內(nèi)的云冷杉林生物量值，最終反演出整個(gè)研究區(qū)云冷杉林生物量(圖3)，其中回歸模型(圖3A)估算研究區(qū)云冷杉林地上生物量最大值為302.71 t·hm?2，最小值為 0.38 t·hm?2，平均值為 148.66 t·hm?2；BP 神經(jīng)網(wǎng)絡(luò)模型 (圖 3B)估算研究區(qū)云冷杉林地上生物量最大值為 304.71 t·hm?2，最小值為 0.19 t·hm?2，平均值為 143.33 t·hm?2；區(qū)域效應(yīng)混合模型 (圖 3C)估算研究區(qū)云冷杉林地上生物量最大值為 307.45 t·hm?2，最小值為 0.10 t·hm?2，平均值為 147.06 t·hm?2；齡組效應(yīng)混合模型 (圖 3D)估算研究區(qū)云冷杉林地上生物量，最大值為 305.61 t·hm?2，最小值為 0.25 t·hm?2，平均值為 141.48 t·hm?2；兩水平混合效應(yīng)模型 (圖 3E)估算研究區(qū)云冷杉林地上生物量最大值為 302.43 t·hm?2，最小值為 0.05 t·hm?2，平均值為 141.63 t·hm?2。云冷杉林生物量的整體分布是沿著“三山”(怒山、云嶺、中甸大雪山)縱向分布，符合云冷杉的生長習(xí)性。總體來說，各個(gè)效應(yīng)水平的混合模型對云冷杉林生物量估測范圍相較于回歸模型及BP神經(jīng)網(wǎng)絡(luò)模型較寬，下限下移，上限上移，均值下移，在一定程度上能夠解決生物量遙感估測中低值高估和高值低估問題。

圖 3 研究區(qū)云冷杉林地上生物量反演示意圖Figure 3 Biomass inversion of spruce-fir forests in the study area

4 討論

本研究以小班尺度為研究單位，基于面狀數(shù)據(jù)提取的遙感因子要比點(diǎn)狀數(shù)據(jù)包含更多信息。一般小班地類劃分最小面積為0.067 hm2進(jìn)行森林資源調(diào)查，基于點(diǎn)狀提取遙感因子反射率值不能夠有效代表該小班實(shí)際遙感反射率，故本研究通過分區(qū)統(tǒng)計(jì)，優(yōu)選出能夠代表各小班內(nèi)真實(shí)地物反射率信息統(tǒng)計(jì)值，反射率平均值與生物量相關(guān)性更強(qiáng)，符合統(tǒng)計(jì)學(xué)基本常識[26]。從云冷杉林生物量飽和值來看，本研究利用冪函數(shù)曲線擬合出的迪慶藏族自治州云冷杉林生物量飽和值高于趙盼盼[27]通過球狀模型擬合的針葉林生物量飽和值。這是由于迪慶藏族自治州獨(dú)特的地理位置，豐厚的水氣條件，再加之云冷杉為當(dāng)?shù)貎?yōu)勢樹種，該地云冷杉林生物量均普遍高于其他地區(qū)。

由于缺乏足夠多的樣地信息，很少有研究能充分考慮林分間的異質(zhì)性來構(gòu)建生物量遙感估測模型，尤其是在高海拔、多山地的迪慶藏族自治州，不易開展外業(yè)工作，測樹因子不易獲取[17]。然而，本研究基于迪慶藏族自治州森林資源二類調(diào)查數(shù)據(jù)，有足夠的樣本信息針對云冷杉林林分間的異質(zhì)性，完成生物量估測模型的構(gòu)建；同時(shí)根據(jù)周律等[28]對于森林資源二類調(diào)查數(shù)據(jù)的可靠性驗(yàn)證結(jié)果，本研究構(gòu)建了不同云冷杉林生物量遙感估測模型，探索提高生物量估測精度的方法。從最終擬合模型的精度評價(jià)與檢驗(yàn)結(jié)果看，各個(gè)效應(yīng)水平的混合模型的擬合精度均優(yōu)于回歸模型，且獨(dú)立性檢驗(yàn)指標(biāo)總相對誤差和平均相對誤差也均優(yōu)于回歸模型和BP神經(jīng)網(wǎng)絡(luò)模型。這也在生物量分段誤差檢驗(yàn)結(jié)果中有所表現(xiàn)，混合效應(yīng)模型在一定程度上降低了回歸模型和BP神經(jīng)網(wǎng)絡(luò)模型估測生物量普遍存在的低值高估和高值低估現(xiàn)象，尤其是在飽和閾值之后生物量的估測誤差。這是因?yàn)榛旌闲?yīng)模型能夠針對不同效應(yīng)水平分組數(shù)據(jù)分別構(gòu)建預(yù)估模型。這類似于利用分層思想，在充分考慮林分間的異質(zhì)性下，提高模型的擬合和預(yù)估能力。這與李春明[22]、符利勇等[23]對混合效應(yīng)模型研究結(jié)果一致。

5 結(jié)論

基于面狀數(shù)據(jù)提取遙感因子信息平均值能夠有效代表真實(shí)地物遙感因子反射率信息，與生物量相關(guān)性更高；以 Landsat 8 OLI B6 波段采用冪函數(shù)擬合出迪慶藏族自治州云冷杉林生物量飽和值為 233 t·hm?2。

充分考慮林分間異質(zhì)性各效應(yīng)水平的混合模型均提高了回歸模型的擬合精度，獨(dú)立性檢驗(yàn)指標(biāo)均優(yōu)于回歸模型和BP神經(jīng)網(wǎng)絡(luò)模型，其各個(gè)生物量分段平均殘差也均有所降低，更大的估測范圍顯著降低了一般模型生物量遙感估測的低值高估尤其飽和閾值之后高值低估的影響，提高了預(yù)估精度。