基于聚類分析算法的鋰離子電芯一致性分選

王焰輝,黃志福,林宇星,劉建煒

( 1. 福州理工學院商學院,福建 福州 350506; 2. 華僑大學信息科學與工程學院,福建 廈門 361021;3. 中國人民銀行泉州市中心支行,福建 泉州 362000; 4. 福州大學土木工程學院,福建 福州 350108 )

電池組中單體電池的不一致性不僅影響對荷電狀態、健康狀況等參數的正確判斷,而且還會造成電池組容量衰減和壽命縮短,甚至引發安全問題。 已有學者針對電芯一致性分選配組方法展開大量研究。 K.Z.Fang 等[1]結合人工神經網絡,基于電池的充電熱性能,將電池分選為不同熱狀態的組別;J.B.Zhang 等[2]采用電化學阻抗譜和等效電路參數篩選電池;Y.Jiang 等[3]基于增量容量分析,提出一種時效機制的篩選策略。 以上研究方法均是基于單體電芯的檢測,配組效率較低,無法滿足大規模電池一致性分選要求。

在此研究背景下,本文作者基于實驗測試所得1 024 只鋰離子電池電芯的數據,以STATA、SPSS 和MATLAB 等軟件為基礎,引入KOHONEN 網絡聚類法、廣義神經網絡回歸聚類算法、傳統的系統聚類法及模糊C 均值(FCM)聚類法,進行橫向對比,研究電芯一致性分選問題,探究更有效的分選配組策略,為實際應用提供判斷依據。

1 數據預處理

1.1 數據獲取

實驗測試用電芯為ICR18650-3200 鈷酸鋰鋰離子電池電芯(江門產),共1 024 只,從00001 編號至01024。 電芯的標稱電壓為3 700 mV,標稱容量為3 200 mAh。

用BAT-NEPDQ-01B-V016 星云鋰離子電池組成品測試系統(福州產)進行測試,數據在兩種情況下得出。 數據集1是將這批電芯經過系列充放電工序[以0.5C(1 600 mA)恒流充電至4.2 V,轉恒壓充電至電流為10 mA,簡稱恒流-恒壓充電,以0.5C恒流放電至電壓為3.0 V]后,在溫度(25±2) ℃、相對濕度65%±20%的環境下,以恒流-恒壓充電得出的數據;數據集2 是將這批電芯先恒流-恒壓充電后,以0.5C恒流放電60 min 得出的數據。

1.2 篩選不合格電芯

在正式分選配組和組裝電池模塊前,快速篩選不合格的電芯。 首先,根據目前國內電池廠商對電芯的配組要求篩選不合格電芯,如容量不低于3 000 mAh,電壓不低于3.290 V,內阻不高于60 mΩ,溫升不高于40 ℃,按標準文件退庫。 鋰離子電池的質量、性能及使用穩定性雖然取決于電壓和內阻,但要達到理想的使用效果和使用時長,關鍵還是取決于存儲容量。 在放電時,電池的電壓隨電量的減少會逐漸降低,并且有相當大的斜率,因此,通過目前常用的鋰離子電池開路電壓對容量的關系,進一步篩選不合格電芯,以完成大樣本數據下實驗數據的預處理。

2 不同聚類算法下電芯快速分選配組

2.1 分選變量的獲取

在進行多參數分選前,需要確定分選變量,分選變量應以電池性能一致性的表現形式為依據進行選擇。 參考李波等[4]的研究,結合電池參數與電池電芯一致性的關系,最終選取以0.5C恒流放電60 min 時的電壓(U)、內阻(R)和溫度(t),以及恒流-恒壓充電的實際容量(C0)、電壓(U0)、電阻(R0)、溫度(t0)和壓差(ΔU)等8 個指標作為電池的分選變量。

在國內配組要求和目前主流鋰離子電池的開路電壓和容量標準下,從1 024 只電芯中篩選出950 只作為研究對象,相應的技術參數如表1 所示。

表1 鋰離子電池電芯的分選參數 Table 1 Sorting parameters of Li-ion battery cell

2.2 系統聚類法分選電芯

聚類分析是直接比較各事物之間的性質,將性質相近的歸為一類,性質差別較大的歸入不同類的技術。 圍繞聚類分析思想,在使用系統聚類時,要定義兩個類之間距離測量和樣本之間距離測度的方法。 平方歐式距離(d)應用廣泛,可用來作為i個樣本間距離的衡量標準,表達式見式(1):

式(1)中:xi和xi+1分別代表兩只電池電芯的某個變量。

因為組間連接法的分類效果較好,應用較廣,所以選取該方法對電池聚類。 運用SPSS 軟件對篩選后的950 只電芯的8 個分選變量作系統聚類,得到圖1 所示的譜系圖。

圖1 950 只電芯數據的譜系圖Fig.1 Spectrum of the data of 950 cells

對圖1 進行分析,基于橫斷法觀察分類個數(通常使用一條線截斷分類線來獲得分類結果),為達到同類電芯參數一致的目的,需保證盡可能短的類間距離,因此圖中虛線(即為橫斷截線)把譜系圖直觀地分成了4 個大類,即橫斷線切割過的4 條直線所對應的聚類集合電芯樣本。

2.3 模糊C 均值(FCM)聚類分選電芯

FCM 聚類算法是用隸屬度確定每個元素屬于某個類別程度的一種聚類算法。 FCM 算法把n個數據向量x分為c個模糊類,并求得每類的聚類中心,使模糊目標函數最小。模糊聚類目標函數為:

式(2)中:uij為個體xi屬于第j類的模糊隸屬度;m為模糊權重指數;vj為第j類的聚類中心。

uij和vj的計算公式為:

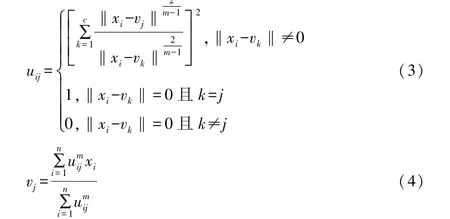
FCM 聚類算法迭代過程如下:

①給定類別數c、模糊權重指數m;

②初始聚類中心v;

③根據式(3)計算模糊隸屬度矩陣u;

④根據式(4)計算每類中心v;

⑤根據式(2)計算模糊聚類目標值,判斷是否滿足結束條件,滿足則算法終止,否則返回步驟③。

FCM 算法最終得到了模糊隸屬度矩陣u,個體根據隸屬度矩陣每列最大元素位置,判斷個體所屬類別。 系統聚類法根據電芯一致性原則將電芯分為4 類;在FCM 算法中,同樣將電芯分選配組為4 類。

2.4 基于KOHONEN 網絡的聚類算法

KOHONEN 網絡是自組織競爭型神經網絡的一種,該網絡為無監督學習網絡,能夠識別環境或產品特征并自動聚類。

使用MATLAB 軟件進行KOHONEN 網絡訓練的步驟可分為以下5 步。

①網絡初始化。 初始化網絡權值w。

②距離計算。 計算輸入向量X=(x1,x2,…,xn)與競爭層神經元j之間的距離dj。

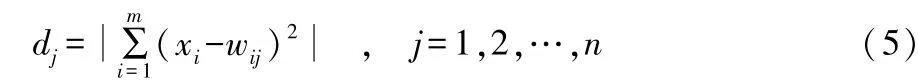
③神經元選擇。 把與輸入向量X距離最小的競爭層神經元g作為最優匹配輸出神經元。

④權值調整。 調整節點g和在領域Ng(t)內包含的節點權系數,即:

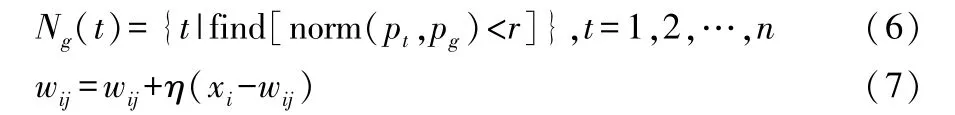
式(6)-(7)中:pg、pt分別為神經元g和t的位置;norm計算兩個神經元之間的歐幾里得距離;find 為查詢非零位置的索引函數;r為領域半徑;η為學習速率。r、η一般隨進化次數的增加而線性下降。

⑤判斷算法是否結束,若沒有結束,則返回步驟②。

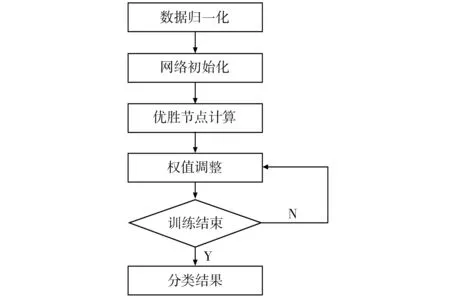
圖2 基于KOHONEN 網絡的聚類算法流程Fig.2 Flow chart of clustering algorithm based on KOHONEN network

基于KOHONEN 網絡的電芯快速分選配組聚類算法流程如圖2 所示。根據電芯分選數據的特點來初始化網絡。 電芯分選數據有8 維,因此輸入層節點數為8。 競爭層節點代表輸入數據潛在的分類類別,考慮到沿用上述4 種分類的效果,選擇競爭層節點數為4 個,將競爭層節點排列在2 行2 列的方陣中。

按式(5)計算和輸入樣本最接近的競爭層節點,作為該樣本的優勝節點。

權值調整時,根據式(6)調整優勝節點領域半徑r內的節點權值,其中領域半徑和學習速率隨著進化過程的深入逐漸變小。 這樣,輸入數據逐漸向幾個節點集中,從而實現網絡聚類的功能。

2.5 廣義神經網絡回歸聚類算法

電池電芯的快速分選配組,需要考慮電壓、電阻、電池溫度和壓差等多種因素,傳統的聚類法,如系統聚類法、FCM 聚類法和K 均值聚類法都存在一定的缺陷和局限性。 在這些方法的基礎上,本文作者提出使用一種改進聚類分析的神經網絡集成方法[5]。

模糊聚類法雖然能夠對電池電芯進行聚類分選,但是由于不同電池的各項參數差別較小,導致部分電池電芯不能準確分類。 采用結合模糊聚類和廣義神經網絡回歸的聚類算法對電池進行分類,流程如圖3 所示。

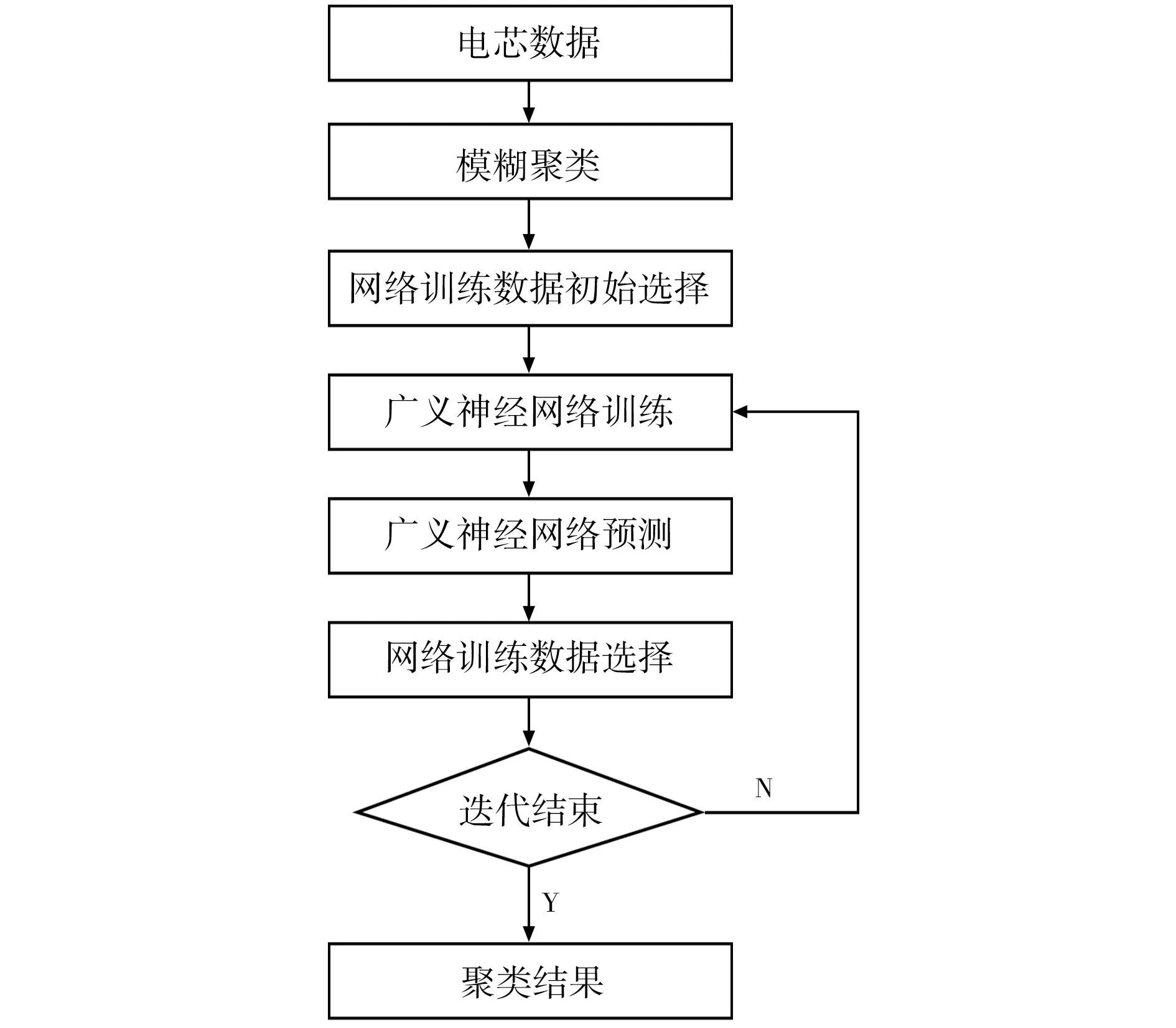
圖3 基于廣義回歸神經網絡的聚類算法流程Fig.3 Flow chart of clustering algorithm based on generalized regression neural network

廣義神經網絡聚類的具體方法如下:首先,用訓練數據訓練廣義神經網絡,使網絡具有電芯快速分選配組的能力;然后,用訓練好的廣義神經網絡來預測樣本所屬的類別,并根據預測結果對樣本重新進行分類;最后,根據樣本重新分類的結果,計算每類的中心,并重新選擇離中心最近的數據,作為網絡訓練數據。 按照上述步驟反復迭代聚類,最終得到分類結果。

2.6 聚類分選結果橫向比較

電壓是電芯一致性判斷的一項重要指標。 為了驗證不同聚類分析算法下分選結果的有效性,將電壓作為聚類分析分選結果的評價指標。 將充電截止電壓(Uce)定義為x軸,放電1 h 電壓(U1h)為y軸,放電截止電壓(Ude)為z軸,對950 只電芯的數據以不同類別構建三維散點圖,分選效果如圖4 所示。

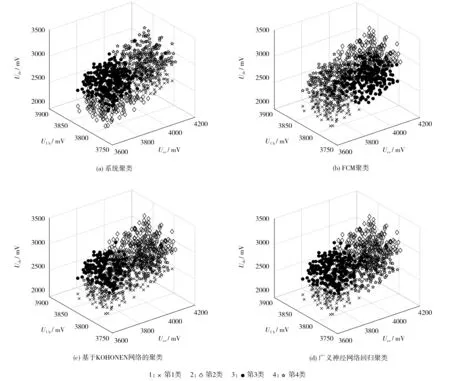
圖4 4 種聚類算法效果圖 Fig.4 Effect diagrams of four clustering algorithms

從圖4 可知,4 種電芯聚類方法的分選結果整體良好。 系統聚類法、FCM 聚類法和廣義神經網絡回歸聚類法的分選結果相似,分成類似“田”字的4 個模塊,在部分數據分組交界的位置,分類稍有差異,分組結果區分度明顯,符合電芯一致性分選配組的原則。 基于KOHONEN 網絡聚類算法的分選結果與其他聚類算法略有不同,最上方左右各有一類,中間分為一類,下方分為一類,最上方兩類表現為充電截止電壓和放電1 h 的電壓較為一致,而中間和下方這兩類表現為放電截止電壓較一致,整體上也達到了電芯一致性分選配組的效果。

除了利用三維散點圖直觀判斷分選結果外,進一步通過計算分選前后充電截止電壓和壓差的標準差變化來驗證分選結果的有效性。 先對符號進行相關定義。

σ(U0)為恒流-恒壓充電的電壓(即充電截止電壓)的標準差;σ′(U0)為分選后所述類別充電截止電壓的標準差;Δσ(U0)為對電芯進行分選前后的充電截止電壓標準差的下降百分比,計算公式為:

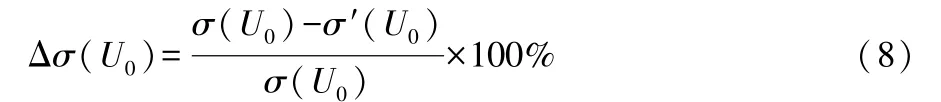
σ(ΔU0)為恒流-恒壓充電的壓差的標準差;σ′(ΔU0)為分選后所述類別恒流-恒壓充電的壓差的標準差;Δσ(ΔU0)的計算公式為:

標準差能反映數據集的離散程度,能更好地判斷電芯分選結果是否符合一致性原則,比較分選前后的充電截止電壓與壓差的標準差變化百分比,有助于深入分析分選效果。

4 種聚類算法的分選結果如表2 所示。

從表2 可知,電芯采用系統聚類法、FCM 聚類法、基于KOHONEN 網絡聚類法和廣義神經網絡回歸聚類算法進行分選,可降低充電截止電壓和壓差的標準差,以滿足電池分選一致性的原則。 從充電截止電壓的標準差來看,分選效果從好到差依次是:廣義神經網絡回歸聚類法、FCM 聚類法、系統聚類法和基于KOHONEN 網絡聚類法;從壓差的標準差來看,分選效果從好到差依次是:KOHONEN 網絡聚類法、廣義神經網絡回歸聚類法、FCM 聚類法和系統聚類法。

由此可見,廣義神經網絡回歸聚類法的整體分選效果最好,基于KOHONEN 網絡聚類法在降低電芯電壓差的標準差,從而提高一致性方面展現出良好的效果。 相較于傳統的系統聚類法和FCM 聚類法,基于KOHONEN 網絡聚類法和廣義神經網絡回歸聚類法的鋰離子電芯一致性的分選,配組效果更佳,可為實際工程應用提供參考。

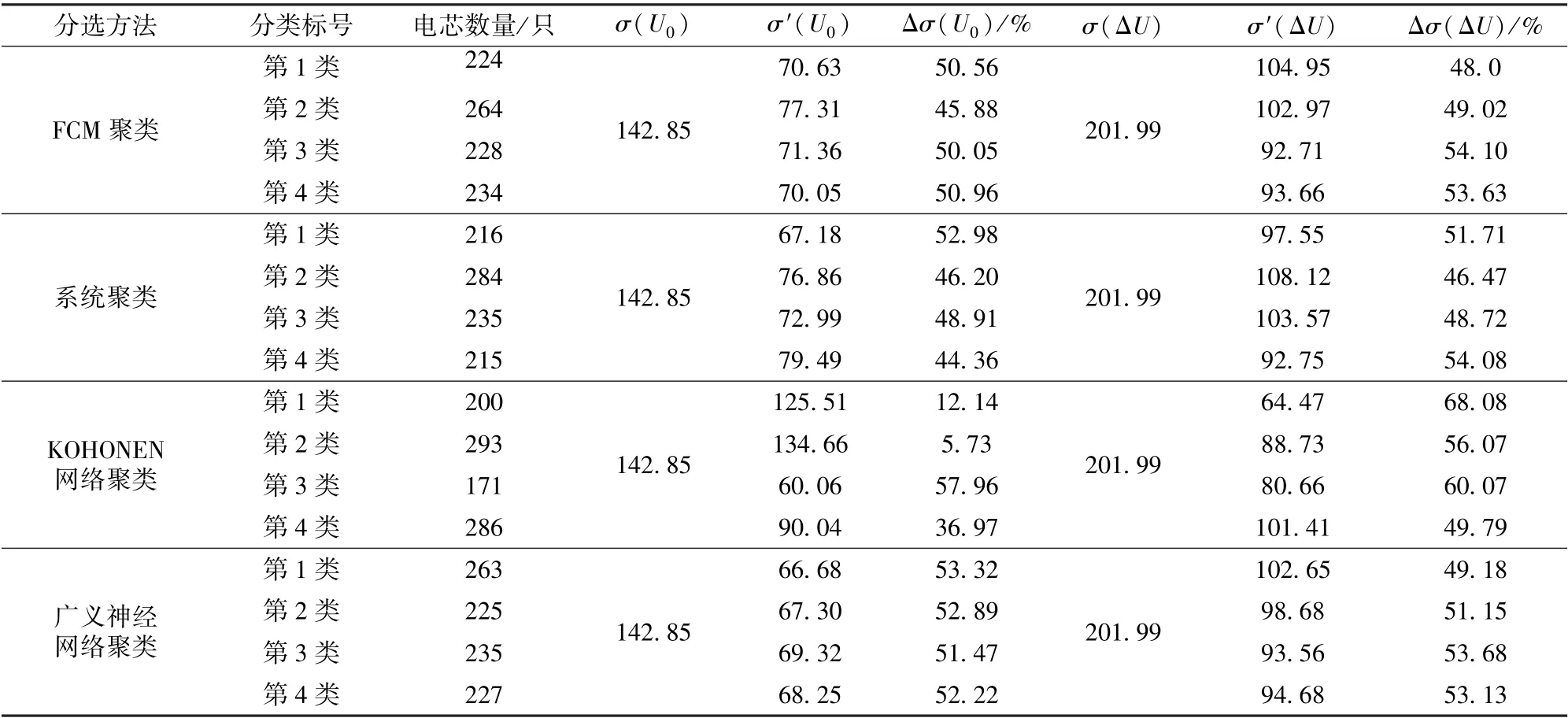
表2 4 種聚類算法分選結果的比較 Table 2 Comparison of sorting results of four clustering algorithms

3 結論

本文作者基于1 024 只鋰離子電池電芯的相關參數,結合電芯一致性原則,確定電芯分選的變量,采用系統聚類法、FCM 聚類法、基于KOHONEN 網絡聚類法和廣義神經網絡回歸聚類法對鋰離子電池電芯進行快速分選配組,最后,多維度評價電芯一致性分選配組效果。

實驗結果表明:相較于傳統的系統聚類法和FCM 聚類法,基于KOHONEN 網絡聚類法和廣義神經網絡回歸聚類法的鋰離子電芯一致性的分選配組效果更好。 摒棄傳統的單體電芯分選法,提出使用神經網絡對電芯進行快速分選配組,即基于KOHONEN 網絡的聚類法和廣義神經網絡回歸聚類法。 今后的研究可進一步考慮其他鋰離子電池電芯分選算法,與現有的分選方法進行多維度的對比,以達到電芯一致性下更高的分選效率和更優的配組效果。