富水深埋隧道圍巖滲透擾動高度計算方法研究

李 姝， 陳煒韜， 方 霖

(1. 四川水利職業技術學院， 四川 成都 611231； 2. 中國電建集團成都勘測設計研究院有限公司，四川 成都 610072； 3. 四川省交通勘察設計研究院有限公司， 四川 成都 610031)

0 引言

隨著我國交通路網的逐漸完善，交通基礎設施建設的重心逐漸向我國西南地區轉移，如川藏公路、川藏鐵路等[1]。我國西南地區具有地勢高差大、地下水資源豐富、生態環境脆弱等地質環境特點[2]。同時，隨著交通基礎設施路網的完善，深埋富水山嶺隧道的修建數量將會日益增多[3]。深埋富水山嶺隧道在施工、運營期通常采用隧道排水系統進行排水泄壓，以降低襯砌背后所受的水壓力，從而保證襯砌結構的穩定。但這種排水泄壓過程會對隧道周邊圍巖滲流場產生明顯的擾動，倘若過度排水，可能會引起地表塌陷、上覆植被缺水死亡等嚴重危害生態環境的現象發生[3]。因此，隧道排水過程對周邊圍巖滲流場的擾動影響問題引起了國內外眾多學者的關注。

目前，國內外針對深埋富水山嶺隧道滲流場擾動問題研究，主要集中在如下方面。

1)采用控制變量法，定性分析不同因素(包括水頭高度、滲透系數、排水率、注漿參數(厚度及注漿壓力)等)對隧道周邊滲流場分布的影響規律，探明不同影響因素下圍巖滲流場的擾動變化過程，且所采用的研究方法主要以數值模擬和室內試驗為主。如： 張梅等[4]分析了注漿厚度、排水率對隧道滲流場分布規律的影響； 李金城[5]、王林等[6]、楊天鴻等[7]研究了水頭高度、滲透系數等因素對圍巖滲流場分布的影響規律； P. A. Witherspoon等[8]分析了裂隙巖體條件下圍巖滲流場的分布規律； D. T. Snow[9]探明了裂隙巖體等效滲透系數與圍巖滲流影響范圍的相互關系； M. Oda[10]明確了節理巖體條件下圍巖滲流場演變規律，給出了節理巖體等效滲透系數的計算方法。

2)分析不同因素對隧道襯砌背后水壓力的影響規律，明確不同影響因素與襯砌背后水壓力的相互關系，并提出相應的水壓力計算方法，且所采用的研究方法主要以理論分析、現場實測、室內試驗為主。如： 王秀英等[11]分析了不同注漿層厚度對圍巖滲流場的影響規律； 劉強等[12]探明了不同排水條件下隧道周邊圍巖滲流場分布規律； M. E. Harr[13]采用鏡像法，給出了隧道圍巖滲流壓力的計算方法； M. Bouvard等[14]和J. O. Bickel等[15]分別基于達西定律與現場實測數據，建立了深埋隧道周邊圍巖滲流壓力理論與經驗計算方法。

從國內外研究現狀總結分析可知，目前針對不同因素對隧道周邊滲流場影響規律研究，多數僅分析了單因素對圍巖滲流場的影響規律，而針對多因素作用下圍巖滲流場擾動規律研究尚不充分。同時，針對不同因素對滲流場擾動的分析多數集中在定性分析，未見針對隧道周邊滲流場擾動影響的相關定量計算方法。

本文首先采用數值模擬方法，探明隧道排水對周邊圍巖滲流場分布的影響規律，提出圍巖滲流擾動高度概念，并將圍巖滲流擾動高度作為評價隧道排水對滲流場擾動程度的評價指標；進而，采用控制變量法，分別分析水頭高度、隧道排水率以及圍巖滲透系數對圍巖滲流擾動高度的影響規律；最后，采用數理擬合方法，給出圍巖滲流擾動高度的計算方法，并采用室內模型試驗對所提出的計算方法進行驗證。

1 依托工程概況

本文以青藏高原地區派墨公路多雄拉隧道為工程依托，分析不同因素條件(水頭高度、圍巖滲透系數、隧道排水率)對隧道周邊圍巖滲流場擾動的影響。該公路隧道開挖直徑為9.13 m，采用1臺雙護盾TBM單向掘進，隧道采用預制管片作為襯砌支護結構。隧道襯砌管片直徑為8.1 m、寬度為1.8 m、厚度為0.35 m,其拼裝方式如圖1(a)所示。該公路隧道最大埋深為812 m、平均埋深為400 m以上，隧道最大水頭高度為120 m，屬富水深埋山嶺隧道。

隧道水頭較高，且地下水補給豐富。依托隧道采用泄水孔排水系統，對預制管片襯砌背后水壓力進行排水泄壓。每環預制管片布設2個泄水孔，分別布置在隧道左、右兩側墻角位置處，如圖1(b)和圖1(c)所示。隧道排水過程如下： 首先，通過每環預制管片上的泄水孔將襯砌背后地下水由泄水孔引流至隧道底部；進而，通過隧道底部排水通道直接將地下水排出隧道洞外，以實現襯砌背后水壓力的泄壓，同時保證隧道洞內不產生積水。

(a) 隧道襯砌管片拼裝方式

(b) 預制管片泄水孔

(c) 現場泄水孔排水過程

2 富水深埋隧道滲流場數值模擬

2.1 數值計算模型

為考慮上述不同因素對富水深埋隧道周邊圍巖滲流場的影響，采用Flac3D數值模擬軟件中滲流場分析模塊，建立圍巖-隧道三維計算模型，分別分析水頭高度、圍巖滲透系數、隧道排水率對隧道周邊圍巖滲流場的影響。其中，數值模擬分析計算過程服從以下假定： 1)圍巖為連續均質各向同性介質； 2)圍巖滲流服從Darcy定律； 3)圍巖處于飽和狀態。

圍巖-隧道三維計算模型如圖2(a)所示。模型x軸方向長度為600 m，y軸方向長度為600 m，z軸方向長度為0.35 m，隧道頂面距模型頂面400 m，即該模型可模擬最大水頭高度為400 m。數值模型邊界條件如下： 模型左、右側及頂面分別為透水邊界，邊界處水流可自由流動； 模型底面為不透水邊界，滲透系數為0。隧道襯砌結構，根據圖1中管片結構尺寸進行構建，如圖2(b)所示。圍巖-隧道三維數值模型中圍巖、襯砌管片均采用實體單元模型，滲流本構模型為各項同性滲流模型，數值模擬模型單元總數為40 876個，節點總數為225 256個。圍巖和襯砌單元均為實體單元，本構模型為各向同性滲流本構模型，孔隙率為0.3%，體積模量為2 GPa，流體抗拉強度為0。

(a) 圍巖-隧道三維模型

(b) 管片襯砌三維模型

2.2 數值模擬監測點布置

為方便監測不同因素對隧道周邊滲流場的影響，在數值模型中設置滲流壓力測線，其測線布置方式以隧道中心為原點，每間隔15°布設1條放射狀測線，且每條測線中以10 cm間隔布置測點。圍巖滲流壓力監測點布置如圖3所示。

2.3 數值模擬計算工況

采用控制變量法，分別分析水頭高度、滲透系數、排水率3個因素條件下周邊圍巖滲流場分布規律。以滲透系數作為數值模擬主要工況劃分指標，制定5組主要工況；其中，每組主要工況中又根據水頭高度、排水率制定84組細分工況，故數值模擬工況數目總計420組。數值模擬工況如表1所示。

圖3 數值模型監測點布置圖

表1 數值模擬工況

隧道不同排水率工況模擬實現方式如下： 首先將隧道襯砌結構設為透水材料，通過調整襯砌結構的滲透系數，使其襯砌結構具有不同程度的排水能力； 進而，對襯砌結構滲透系數進行試算，同時獲取試算滲透系數條件下經由襯砌結構排出的水量，并結合隧道涌水量計算得出襯砌結構試算滲透系數條件下隧道排水率； 最后，根據排水率細分工況，不斷調整襯砌結構滲透系數，直至獲得滿足各排水率工況要求的襯砌結構滲透系數，以此實現不同排水率細分工況的模擬。

2.4 數值模擬計算流程

1)建立圍巖-隧道三維數值模型，設置滲流場邊界條件與圍巖、襯砌實體參數，進行水頭高度條件下圍巖滲流場初始平衡計算，得到隧道開挖前圍巖初始靜水壓力滲流場。

2)進行隧道毛洞開挖模擬，采用FISH語言獲得隧道涌水量。

3)進行隧道襯砌支護，同時將其滲流本構模型設置為透水材料；并根據排水率細分工況要求，設置襯砌結構滲透系數，進行不同排水率工況下圍巖滲流場計算，直至計算收斂。

4)通過設置的數值模擬測線，獲得該工況下隧道周邊圍巖滲流場分布規律。

3 圍巖滲流擾動高度及影響因素分析

3.1 圍巖滲流擾動高度概念

以水頭高度90 m、滲透系數1×10-2cm/s為例，分別給出隧道排水率為0(即不排水)與排水率為100%時隧道周邊圍巖滲流場的分布規律，如圖4所示。

(a) 排水率為0時圍巖滲流場(單位： Pa)

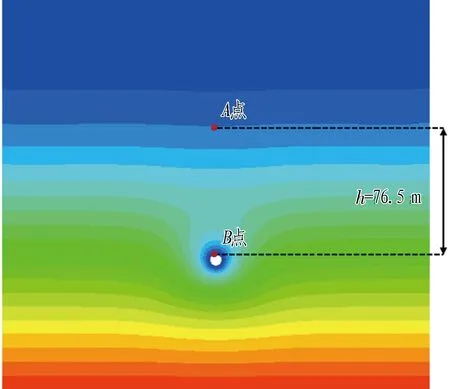
(b) 排水率為100%時圍巖滲流場

由圖4(a)可知： 當隧道排水率為0時，此時圍巖滲流壓力線呈水平分布，同一水頭高度處各點滲流壓力相等，圍巖整體滲流壓力分布為靜水壓力分布狀態，并且襯砌背后水壓力量值近似等于靜水壓力值，說明隧道不進行排水時不會對圍巖滲流場產生擾動，不影響圍巖滲流場初始分布狀態，這點與目前大多學者研究結論一致[3,6,12,15]。

由圖4(b)可知： 1)當隧道排水后，隧道周邊滲流場發生明顯擾動現象，隧道周邊滲流場由原本的靜水壓力狀態轉變為動水壓力狀態，其中最為顯著的變化為隧道拱頂上部位置的圍巖滲流壓力線分布形態由水平線轉變為“漏斗”形態的曲線，隧道拱頂位置上方圍巖滲流壓力明顯降低； 2)對比排水與不排水條件下隧道拱頂上方圍巖滲流場分布規律可知，由隧道排水所引起的圍巖滲流場擾動范圍并不會擴散至整個圍巖范圍，而僅在隧道拱頂上部一定范圍內存在。

為了準確評價隧道排水過程對圍巖滲流場擾動的影響，本文提出圍巖滲流擾動高度概念，即為在隧道埋深方向上(y軸)隧道排水前后圍巖滲流壓力不發生變化位置(A點)與隧道拱頂位置(B)處的最小距離。根據圍巖滲流擾動高度定義，圖4(b)中隧道排水率為100%條件下，圍巖滲流影響高度為76.5 m。

3.2 不同影響因素下圍巖滲流擾動高度

圍巖滲流擾動高度受到滲透系數、水頭高度以及隧道排水率的綜合影響。采用控制變量法，分別分析上述3個因素對圍巖滲流擾動高度的影響規律。

3.2.1 不同滲透系數條件下圍巖滲流擾動高度

不同滲透系數條件下圍巖滲流擾動高度如圖5所示。可以看出： 給定水頭高度與隧道排水率時，隨著圍巖滲透系數的增加，圍巖滲流擾動高度呈逐漸增加趨勢，兩者呈正相關關系。

圖5 不同滲透系數條件下圍巖滲流擾動高度

以水頭高度120 m為例，當圍巖滲透系數為1×10-6cm/s時，此時圍巖滲流擾動高度為10.7 m； 而當圍巖滲透系數增大至1×10-2cm/s時，圍巖滲流擾動高度增大至106.47 m，增大了895. 05%。

3.2.2 不同隧道排水率條件下圍巖滲流擾動高度

以水頭高度90 m為例，不同隧道排水率條件下圍巖滲流擾動高度如圖6所示。可以看出： 給定水頭高度與圍巖滲透系數時，隨著隧道排水率的增加，圍巖滲流擾動高度呈逐漸增加趨勢，兩者亦呈正相關關系。

以滲透系數1×10-2cm/s為例，當隧道排水率為20%時，此時圍巖滲流擾動高度為67.54 m； 當排水率增大至100%，圍巖滲流擾動高度增大至77.48 m，增大了14.7%。

3.2.3 不同水頭高度條件下圍巖滲流擾動高度

圍巖滲流擾動高度隨水頭高度變化曲線如圖7所示。可以看出： 圍巖滲流擾動高度隨水頭高度變化曲線呈現出明顯的2段式特征。1)當水頭高度小于某一水頭高度時(圖中A′B′段)，隨水頭高度的增加，圍巖滲流擾動高度呈現出較為明顯的線性增大趨勢。以排水率100%工況為例，當水頭高度為60 m時，圍巖滲流擾動高度為55.46 m； 當水頭高度增大至120 m時，此時圍巖滲流擾動高度為109.24 m，增大了96.97%。2)當水頭高度大于某一水頭高度時(圖中B′C′段)，此時圍巖滲流擾動高度表現為定值，不再隨水頭高度的增加而繼續增加。

圖6 不同隧道排水率條件下圍巖滲流擾動高度

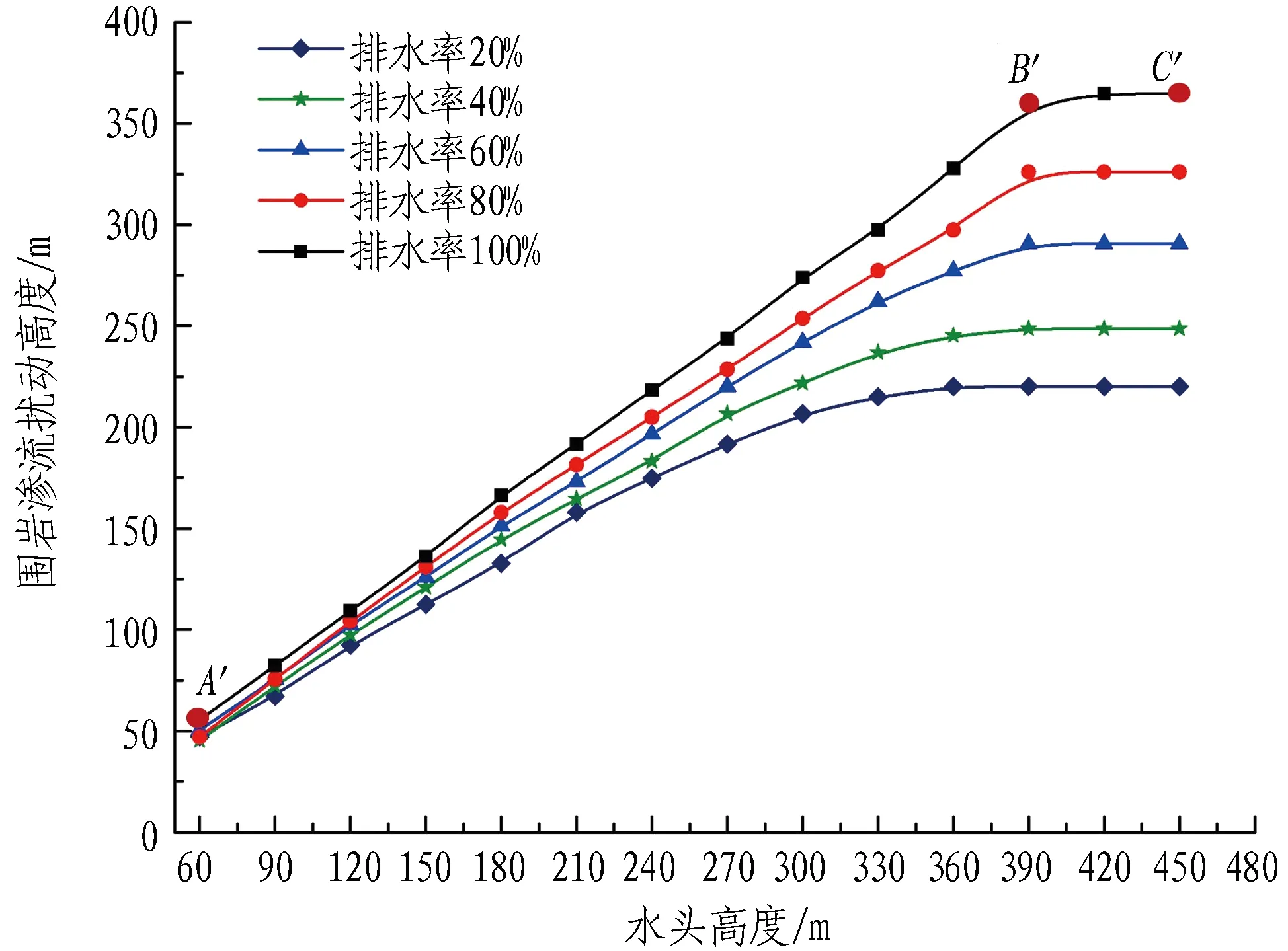
圖7 圍巖滲流擾動高度隨水頭高度變化曲線

為了更好地描述圍巖滲流擾動高度隨水頭高度的變化規律，將B′點對應的水頭高度定義為臨界水頭高度，對應的圍巖滲流擾動高度定義為臨界圍巖滲流擾動高度。同時，對比水頭高度、滲透系數、隧道排水率3個影響因素，其中對圍巖滲流擾動高度影響程度最大的為滲透系數因素；而排水率雖然是圍巖滲流擾動高度產生的根本因素，但其自身對圍巖滲流擾動高度影響最小。因此，可得滲透系數、水頭高度、隧道排水率對圍巖滲流擾動高度影響程度依次降低。

4 圍巖滲流擾動高度計算方法

由上文分析可知，圍巖滲流擾動高度受到3個因素的綜合影響，所以給出的計算方法中應能體現上述3個影響因素。首先根據上述水頭高度與圍巖滲流擾動高度的相互關系，給出圍巖滲流擾動高度隨水頭高度變化模型及數學表達式如下：

當H>H臨界時，h=h臨界；

(1)

當H≤H臨界時，h=aH。

(2)

式(1)—(2)中:H為水頭高度；H臨界為臨界水頭高度；h為圍巖滲流擾動高度；h臨界為臨界圍巖擾動高度；a為待定系數。

若采用式(1)和式(2)對圍巖滲流擾動高度進行計算，還需給出臨界水頭高度、臨界圍巖擾動高度與待定系數的計算方法。

4.1 H>H臨界時圍巖滲流擾動高度計算方法

由式(1)分析可知，當水頭高度大于臨界水頭高度時，此時圍巖擾動高度為定值。下文分別給出臨界水頭高度與臨界圍巖滲流擾動高度計算方法。

由圖5可知，臨界水頭高度受到滲透系數與排水率的綜合影響。本文采用數理擬合方法，基于數值模擬計算結果(見表2)，擬合給出臨界水頭高度計算表達式，如式(3)所示；擬合結果云圖如圖8所示。

表2 不同工況下臨界水頭高度

由圖8可知，臨界水頭高度與排水率、滲透系數呈二次曲面關系，且擬合相關系數為98.3%，擬合結果良好。因此，可采用式(3)對臨界水頭高度進行計算。

H臨界=544.8+0.76β+45.63lnk+4.64βlnk×

10-2+0.87(lnk)2。

(3)

式中：β為排水率，%；k為滲透系數，cm/s。

圖8 臨界水頭高度與排水率、滲透系數擬合云圖

將臨界水頭高度、圍巖滲透系數、隧道排水率作為自變量，臨界圍巖滲透擾動高度作為因變量，擬合得出臨界圍巖滲流擾動高度計算表達式。同時，由于臨界水頭高度計算表達式中因變量為滲透系數與排水率。因此，臨界圍巖滲流擾動高度計算表達式中因變量只有圍巖滲透系數與排水率。下文以滲透系數與排水率作為因變量，對臨界圍巖滲流擾動高度計算表達式進行擬合。不同工況下臨界圍巖滲流擾動高度如表3所示。

表3 不同工況下臨界圍巖滲流擾動高度

臨界圍巖滲流擾動高度與排水率、滲透系數擬合云圖如圖9所示。可以看出： 臨界圍巖滲流擾動高度與排水率、滲透系數呈二次曲面關系，且擬合相關系數為99.42%，擬合結果良好。因此，可采用式(4)對臨界圍巖滲流擾動高度進行計算。

h臨界=459.3+2.78β+74.45lnk+0.21βlnk+

3.05(lnk)2。

(4)

圖9 臨界圍巖滲流擾動高度與排水率、滲透系數擬合云圖

4.2 H≤H臨界時圍巖滲流擾動高度計算方法

由式(2)可知，當水頭高度小于等于臨界水頭高度時，圍巖滲流擾動高度隨著水頭高度的增加呈線性增加趨勢； 且兩者比例系數僅與圍巖滲透系數與排水率有關，而與水頭高度無關。因此，采用數理擬合方式，以滲透系數與排水率作為因變量；比例系數作為自變量進行數理擬合。不同工況下比例系數如表4所示。

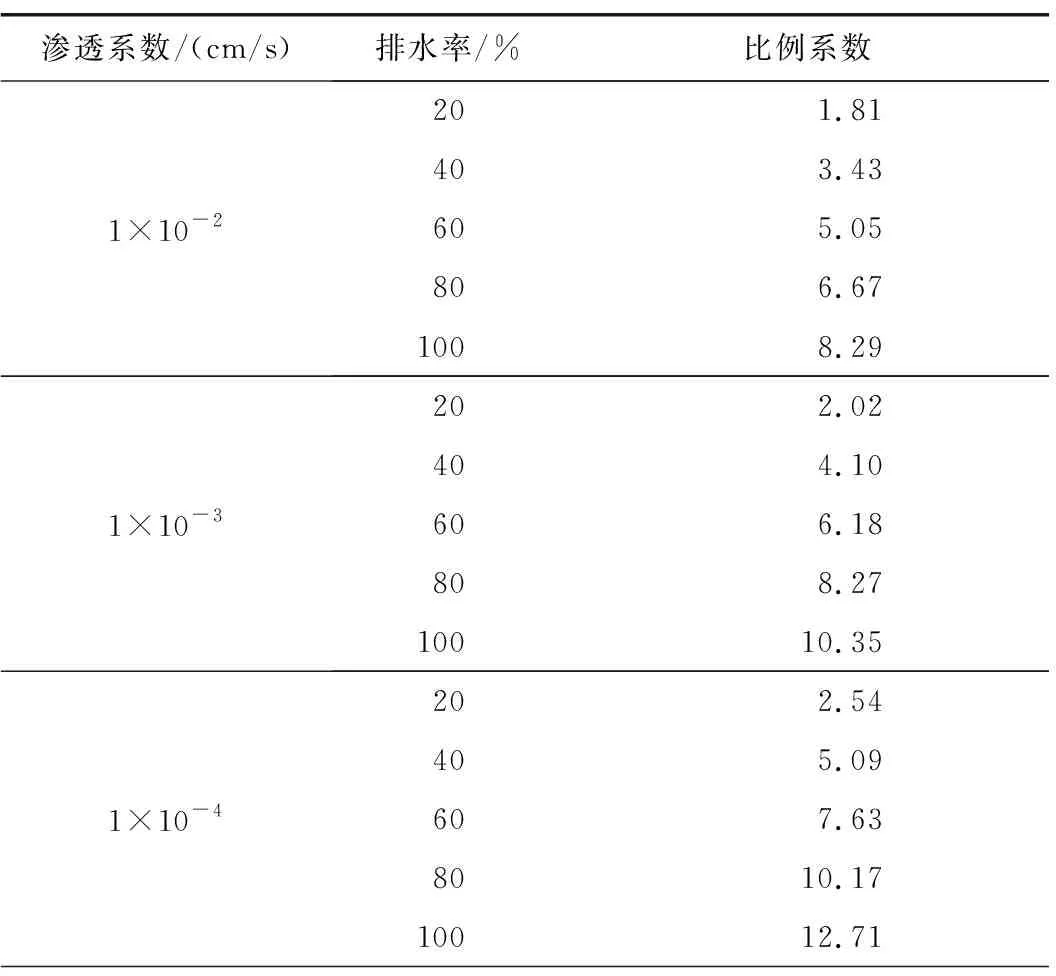
表4 不同工況下比例系數表

表4(續)

比例系數與滲透系數、排水率擬合云圖如圖10所示。可以看出： 比例系數與排水率、滲透系數呈二次曲面關系，且擬合相關系數為99.78%，擬合結果良好。因此，可采用式(5)對比例系數進行計算。

圖10 比例系數與滲透系數、排水率擬合云圖

a=1.6+0.44lnk+3.5β×10-2+2.9(lnk)2×

10-2-0.01βlnk。

(5)

式中a為比例系數。

因此，當水頭高度小于等于臨界水頭高度時，圍巖滲流擾動高度可按式(2)計算，其中比例系數按式(5)計算。

5 圍巖滲流擾動高度計算方法室內試驗驗證

為了驗證本文所提出的圍巖滲流擾動高度計算方法的正確性及合理性，采用室內相似試驗，模擬富水深埋隧道排水條件下圍巖滲流場擾動變化過程，獲得相應圍巖擾動高度，并將其與采用計算方法所得結果進行對比。

5.1 室內相似材料準備

選取幾何相似比、容重相似比、滲透系數相似比為基礎相似比，根據相似三定律[16]，推導出其余相似試驗所需物理量的相似比例關系。室內試驗所需物理量相似比如表5所示。

圍巖相似材料為石英砂與石膏粉的混合料，其中混合料組分比例根據模型試驗滲透系數工況要求確定，以保證圍巖相似材料滲透系數滿足試驗工況滲透系數要求。圍巖相似原材料如圖11所示。

表5 室內試驗所需物理量相似比

(a) 石英砂 (b) 石膏粉

襯砌結構相似材料為PVC圓形管狀材料，襯砌相似結構尺寸為原型結構按幾何相似比縮尺后的相應尺寸。同時，在管片相似結構上開孔，以實現襯砌結構排水。通過控制管片結構開孔數量，可實現不同排水率條件下的管片襯砌排水過程。管片相似結構如圖12所示。

(a) 相似管片外側

(b) 相似管片內側

5.2 試驗工況

結合室內試驗條件，制定了3種不同滲透系數試驗主要工況，且水頭高度均為90 m。其中，每種主要工況下分別細分3種排水率工況。室內試驗模擬工況如表6所示。

表6 室內試驗模擬工況

5.3 試驗裝置及測點布置

5.3.1 試驗裝置

本次試驗在西南交通大學自行設計的大型富水深埋隧道滲流場模擬試驗系統上進行，整套試驗系統由環境箱(4 m×0.7 m×4 m)、控制系統、數據采集系統3部分組成。滲流模擬試驗系統如圖13所示。滲流場控制系統由測壓管和水平平行進、排水花管組成。數據采集系統包括TS-KY-1型高精度微型孔隙水壓力傳感器、靜態數據采集儀、隧道排水采集箱等，實現對隧道周邊滲流場擾動的監測。

(a) 模型試驗

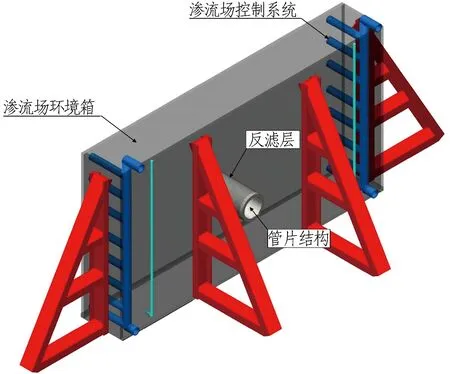
(b) 試驗裝置示意圖

5.3.2 測點布置

選擇沿隧道軸向方向中間位置斷面作為監測斷面，以水平間隔25 cm(約1倍隧道洞徑)布設5根縱向測管；每根縱向測管以垂直間隔20 cm布設滲流壓力測點(所用儀器為微型水壓力計)；同時，管片襯砌背后環向方向亦布設相應測點。室內模型試驗測點布置如圖14所示。

5.4 試驗過程

1)采用配比好的石英砂與石膏粉的圍巖相似材料，將環境箱填筑密實；同時在隧道標高處安裝襯砌管片。

2)采用滲流場控制系統，對環境箱進行注水，使其達到試驗所需的穩定滲流場條件。

3)根據不同排水率細分工況，對管片襯砌開孔進行控制，并在試驗過程中實時采集圍巖滲流場以及隧道排水量數據。

4)將管片襯砌進行拆除，測量該主要工況下隧道涌水量；進而，計算得到隧道排水率。室內模型試驗過程如圖15所示。

5.5 試驗結果驗證分析

將本次不同試驗工況條件下得到的圍巖滲流擾動高度與采用上文提出的圍巖滲流擾動高度計算方法計算所得的結果進行對比分析。圍巖滲流影響高度計算結果對比如圖16所示。

圖16 圍巖滲流影響高度計算結果對比

由圖16可知: 1)給定排水率條件下采用2種方法得到的圍巖滲流擾動高度均隨滲透系數增加而呈現增加趨勢，2種方法反映的對應一致； 2)通過對比給定排水率與滲透系數條件下采用2種方法獲得的圍巖滲流擾動高度量值可知，2種方法所得結果較為接近，差異較小，從而驗證了上文所提的圍巖滲流擾動高度計算方法的正確性及合理性。

6 結論與建議

1)富水深埋隧道排水泄壓過程會對隧道拱頂上方圍巖滲流場產生明顯擾動，隧道上部圍巖滲流壓力等勢線分布由水平分布形態轉變為漏斗狀分布形態。但這種隧道排水擾動僅在隧道拱頂上部一定范圍內存在，將該擾動范圍的縱向高度定義為圍巖滲流擾動高度。

2)圍巖滲透系數、水頭高度以及隧道排水率均與圍巖滲流擾動高度呈正相關關系。通過對圍巖滲流擾動高度影響程度對比可知，排水率是產生圍巖滲流場擾動的根本因素，但其對圍巖滲流擾動高度影響最小，影響程度最大的因素為圍巖自身的滲透系數。

3)當給定滲透系數與排水率時，隨水頭高度增加，圍巖滲流擾動高度變化呈2段式變化特征。當水頭高度小于等于臨界水頭高度時，圍巖滲流擾動高度與水頭高度呈線性正相關關系；當水頭高度大于臨界水頭高度時，圍巖滲流擾動高度不再隨水頭高度繼續變化，趨于定值。

4)采用數理擬合方法，分別給出了臨界水頭高度、臨界圍巖滲流擾動高度計算表達式；根據水頭高度與圍巖滲流擾動高度相互關系，給出了圍巖滲流擾動高度計算方法；并采用室內相似試驗對所提計算方法進行了對比，驗證了所提計算方法的正確性及合理性。

本文在計算襯砌背后水壓力量值時，所用方法相對較為簡單，與實際存在一定差別，下一步建議探討襯砌背后各點水壓力的計算方法。