盾構隧道斜螺栓連接環縫剪切破壞特征理論解析

何 源， 楊振華， 柳 獻， *， 丁文其

(1. 中交二航局第三工程有限公司， 江蘇 鎮江 212000; 2. 同濟大學， 上海 200092)

0 引言

工程實踐表明，在盾構隧道沿縱向不均勻沉降的過程中，管片本體的變形很小，變形主要集中在環縫附近。另一方面，環縫是一類由螺栓連接的不連續構件，其強度遠遠低于管片本體，其承載能力直接決定隧道的承載能力。為了提高隧道的正常使用性能和極限承載能力，有必要研究盾構隧道環縫的受力性能及其破壞機制。

現有盾構隧道環縫受力性能的研究主要分為2類，部分學者采用解析解法對環縫的受力性能展開研究。志波由紀夫[1]給出了1組公式，用于計算環縫的抗彎剛度。隨后，許多學者針對志波模型的不足之處進行了修正，考慮了更多的影響因素。如： 廖少明[2]提出了環縫影響范圍的概念，修正了志波由紀夫的理論，使計算出的環縫抗彎剛度更加貼近實際； 徐凌[3]在計算環縫抗彎剛度的過程中考慮了環縫斷面上壓力的影響，能夠更加合理地貼近管片環的真實邊界條件； 魯志鵬[4]、周寧等[5]綜合考慮了螺栓預應力和環縫影響范圍對環縫抗彎剛度的影響； 張文杰等[6]考慮了橫向剛度和環縫影響范圍對環縫抗彎剛度的影響； 葉飛等[7]考慮了橫向剛度和橫向變形對環縫抗彎剛度的影響。解析解的優勢是概念清晰，且當計算參數發生變化時能夠很快得到解答。現有研究主要關注環縫的抗彎性能，對環縫的抗剪性能研究相對比較缺乏。而實際上，環縫錯臺是工程中的常見現象。在錯臺條件下，環縫以抗剪為主，環縫斷面上的彎矩很小。因此，有必要進一步發展求解環縫抗剪性能的解析方法。

部分學者采用足尺試驗的方法對環縫受力性能展開研究。如： 閆治國等[8]以青草沙輸水隧道為研究對象，進行了一系列足尺試驗，其研究結果表明，環縫的剪切破壞過程分為3個階段； 朱瑤宏等[9]基于寧波軌道交通隧道進行了一系列足尺試驗，獲取了不同縱向壓力下環縫的抗剪剛度； 李冬梅等[10]基于上海長江隧道進行了足尺試驗，并依據試驗結果歸納出了一系列公式，用于計算不同錯臺條件下環縫的抗剪剛度； J. Buco等[11]通過足尺試驗，對地下混凝土管道的拉彎剪復合作用進行了試驗研究； T. Putke等[12]對環縫各受力構件(剪力銷、凹凸榫)在環縫破壞過程中所起到的作用進行了足尺試驗研究； A. Salemi等[13]通過足尺試驗對環縫抗剪剛度與環縫斷面縱向壓力的關系進行了研究。足尺試驗中管片的邊界條件最接近于實際工程，其結果具有較高的準確性。但是，現有研究其結果主要來自對試驗數據的歸納，而很少基于力學原理對環縫的破壞機制進行解析。

綜上所述，現有關于環縫受力性能的理論研究，主要關注抗彎機制，很少涉及到抗剪機制，且現有的足尺試驗研究與理論研究之間缺乏聯系。為改進現有研究的不足，本研究以某斜螺栓連接大直徑盾構隧道環縫為研究對象，首先設置1組足尺試驗，揭示其破壞機制； 隨后采用計算力學的方法，將其破壞機制推廣到構造相似的其他斜螺栓連接環縫； 最后通過敏感性分析，揭示各因素對斜螺栓連接環縫抗剪剛度的影響。

1 斜螺栓連接環縫剪切破壞足尺試驗

1.1 研究對象與試驗構件

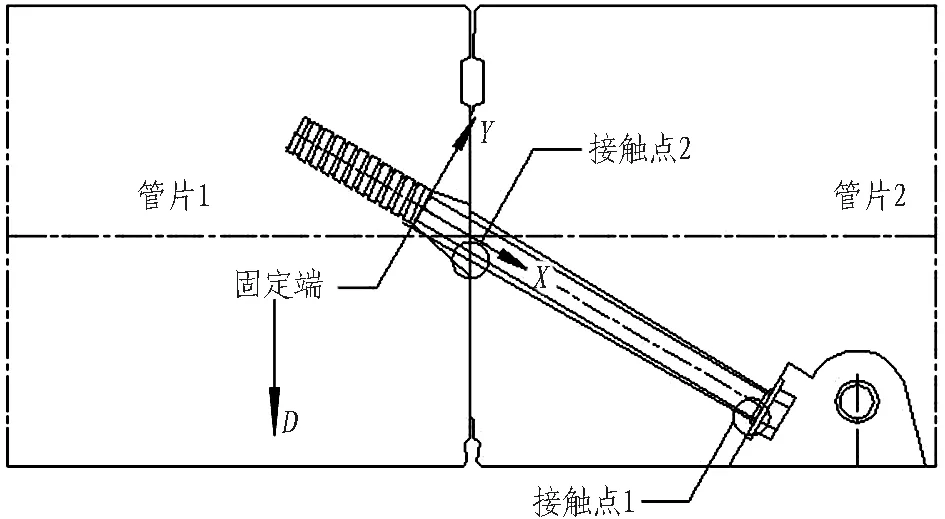
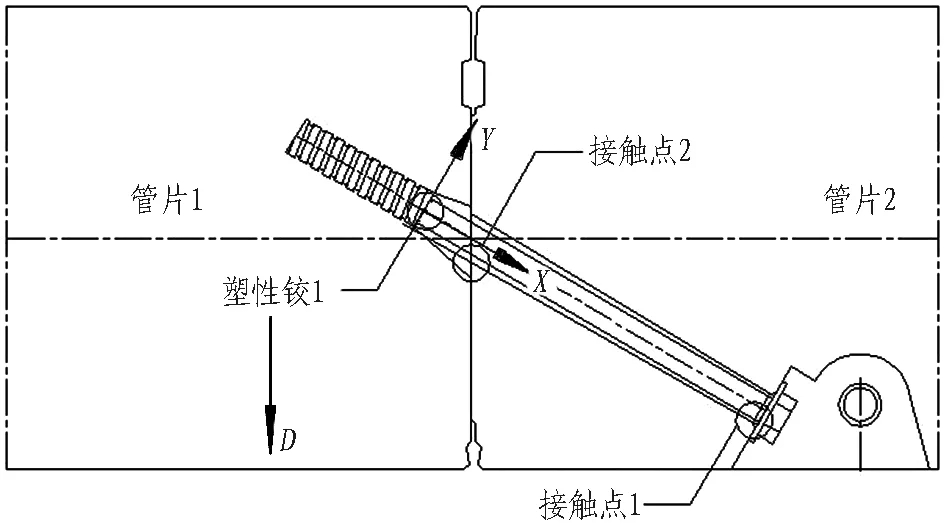
以某大直徑越江隧道環縫為研究對象，進行足尺試驗。該隧道外徑為11 800 mm，內徑為10 800 mm，環寬為2 m，壁厚為500 mm，環縫由46根M30斜螺栓連接。環縫的細部構造如圖1所示。斜螺栓總長度為588 mm，其中與套筒連接的螺牙段長度為160 mm，螺桿光滑段長度為428 mm。斜螺栓與水平方向的夾角為30°。

本次試驗的構件由3塊管片構成。剪切塊1和剪切塊3的長度為350 mm，剪切塊2的長度為2 700 mm，3塊管片的高度均為500 mm。環縫尺寸與原隧道完全相同。試驗構件如圖2所示。

1.2 加載設備與測試方案

本次試驗所采用的加載設備如圖3(a)所示，在加載設備作用下試驗構件的受力簡圖如圖3(b)所示。本次試驗施加2個方向的荷載。其中豎向荷載2F由豎向千斤頂通過2根分配梁施加到試驗構件上，該荷載模擬的是環縫剪力。水平荷載FN通過水平向千斤頂通過輔助鋼構件施加到試驗構件上，該荷載模擬的是環縫斷面上作用的縱向壓力。由構件的受力簡圖可知，環縫剪力等于豎向荷載的1/2，大小為F。

圖1 某越江隧道環縫構造 (單位： mm)

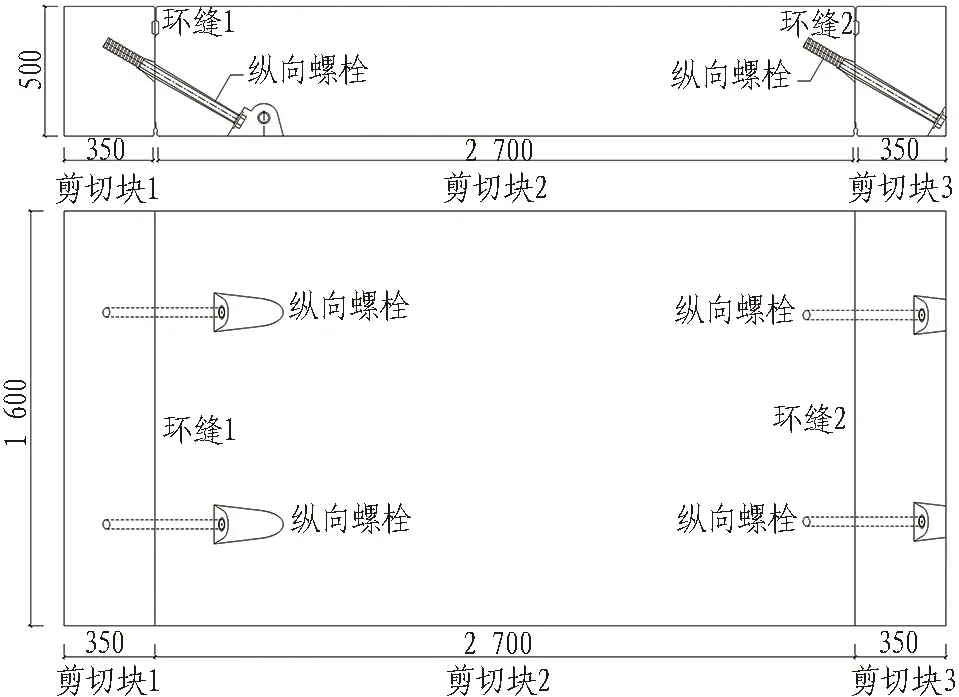
圖2 試驗構件(單位： mm)

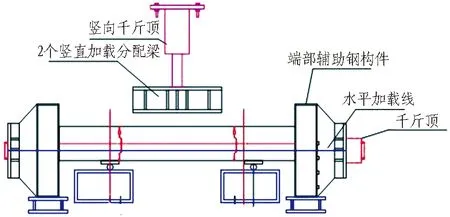
(a) 加載設備

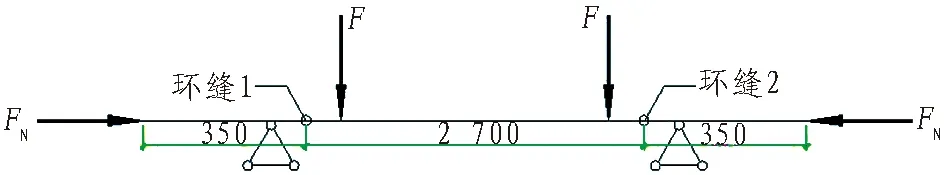
(b) 受力簡圖

本次試驗在2條環縫上共布置12個位移計，用于測量環縫錯臺。測點布置如圖4所示。

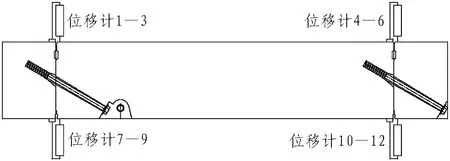
圖4 測點布置

1.3 試驗工況及加載方案

本次試驗設置的工況為模擬隧道掘進過程中環間產生錯臺時管片環的受力狀態。假定隧道掘進過程中盾構的頂推力在環面上均勻分布，則依據施工過程中實測的盾構頂推力，算得試驗構件1.6 m寬度上分配到的壓力約為500 kN。在加載過程中，首先將水平荷載FN加載至500 kN，隨后維持水平荷載FN不變，逐級施加垂向荷載F，每級10 kN，直至試驗構件發生破壞。

1.4 試驗現象

試驗后，拆解試驗構件，觀察到環縫斜螺栓如圖5所示。

圖5 試驗后的環縫斜螺栓

由圖5可知: 環縫斜螺栓在加載過程中出現了2個明顯的塑性鉸區，其中塑性鉸1位于螺牙段和螺桿光滑段的交界點，塑性鉸2位于環縫接觸面附近。

1.5 試驗結果

本次試驗實測的環縫錯臺-環縫剪力關系如圖6所示。

圖6 環縫錯臺-環縫剪力關系

由圖6可知，不論環縫1還是環縫2，其破壞過程均分為3個階段： 第1階段環縫抗剪剛度近乎無窮大，第2階段環縫抗剪剛度幾乎為0，第3階段環縫抗剪剛度隨錯臺發展不斷變化。

2 環縫破壞全過程解析

2.1 研究對象

第1節中所述環縫剪切足尺試驗展示了某一具體隧道的環縫剪切破壞過程，本節將通過解析解法對上述破壞過程的機制進行分析，并將其推廣到結構類似的其他斜螺栓連接盾構隧道環縫。

典型斜螺栓及螺栓孔構造如圖7所示。其中C為管片2螺栓孔下邊緣與環縫的交點，B為管片1螺栓孔上邊緣與環縫的交點。為便于描述，以斜螺栓光滑段和螺牙段的交點O為原點，沿斜螺栓軸向布置X軸，垂直螺栓軸向布置Y軸，建立平面直角坐標系。

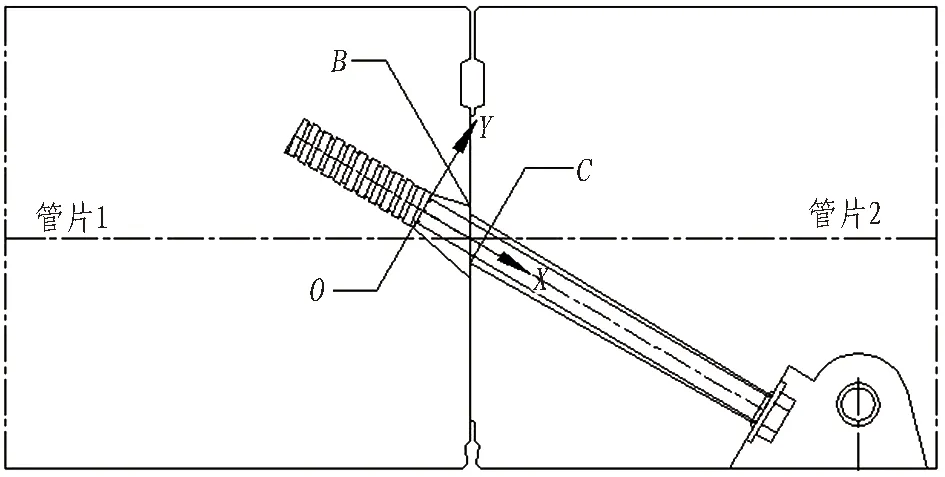
圖7 典型斜螺栓及螺栓孔構造

2.2 環縫破壞過程分析

由圖6可知，環縫1與環縫2的破壞過程截然不同。其原因在于，對于圖7所示構造的斜螺栓連接環縫，斜螺栓一端咬合于套筒中(以下稱為錨固端)，一端穿過手孔(以下稱為活動端)。錨固端相對于活動端向上錯動或是向下錯動，斜螺栓的破壞機制不同，環縫的受力性能也不相同。

2.2.1 錨固端相對于活動端向下錯動環縫破壞過程

錨固端相對于活動端向下錯動時，環縫的破壞過程如圖8所示。圖中f表示環縫接觸面上作用的摩擦力。假定管片1相對于管片2向下錯動，管片2施加在管片1上的摩擦力方向向上，管片1施加在管片2上的摩擦力方向向下。

由圖8可知： 1)當相鄰2環管片由于某種原因產生相對運動趨勢時，環縫斷面上的靜摩擦力首先發揮作用。在環縫剪力不超過最大靜摩擦力時，環縫錯臺不會發展。將此階段定義為環縫破壞過程的第1階段。2)當環縫剪力略大于環縫最大靜摩擦力時，由于螺栓孔和螺栓之間存在間隙，在環縫剪力不增加的情況下環縫錯臺將產生數mm的發展。將此階段定義為環縫破壞過程的第2階段。3)當斜螺栓與螺栓孔產生第1個接觸點時，環縫剪力的增量將由斜螺栓單獨承擔。隨著環縫錯臺的逐漸增大，斜螺栓與螺栓孔之間的接觸點將逐漸增加，斜螺栓將依次產生2個塑性鉸，環縫因此喪失承載能力而破壞。將此階段定義為環縫破壞過程的第3階段。

應該指出，由于管片1相對于管片2向下錯動，所以在第3階段斜螺栓斷面上不會產生任何軸力，斜螺栓以受彎為主。在不同錯臺條件下，斜螺栓的支撐條件不同，斜螺栓的抗彎剛度亦有所不同，因此導致環縫抗剪剛度發生變化。

2.2.2 錨固端相對于活動端向上錯動環縫破壞過程

當錨固端相對于活動端向上錯動時，環縫的破壞過程如圖9所示。

由圖9可知： 錨固端相對于活動端向上錯動時，環縫破壞過程的第1階段、第2階段與錨固端相對于活動端向下錯動時完全相同；但是在第3階段，由于螺母與螺栓孔端面之間會產生較大的擠壓力N，導致斜螺栓全斷面受到大小為N的拉力，在斜螺栓與螺栓孔的第2個接觸點產生之前，斜螺栓就會拉壞； 整個第3階段斜螺栓以受拉為主，剛度不變，因此整個第3階段環縫的抗剪剛度也不發生變化；這是與錨固端相對于活動端向下錯動的情形截然不同的。

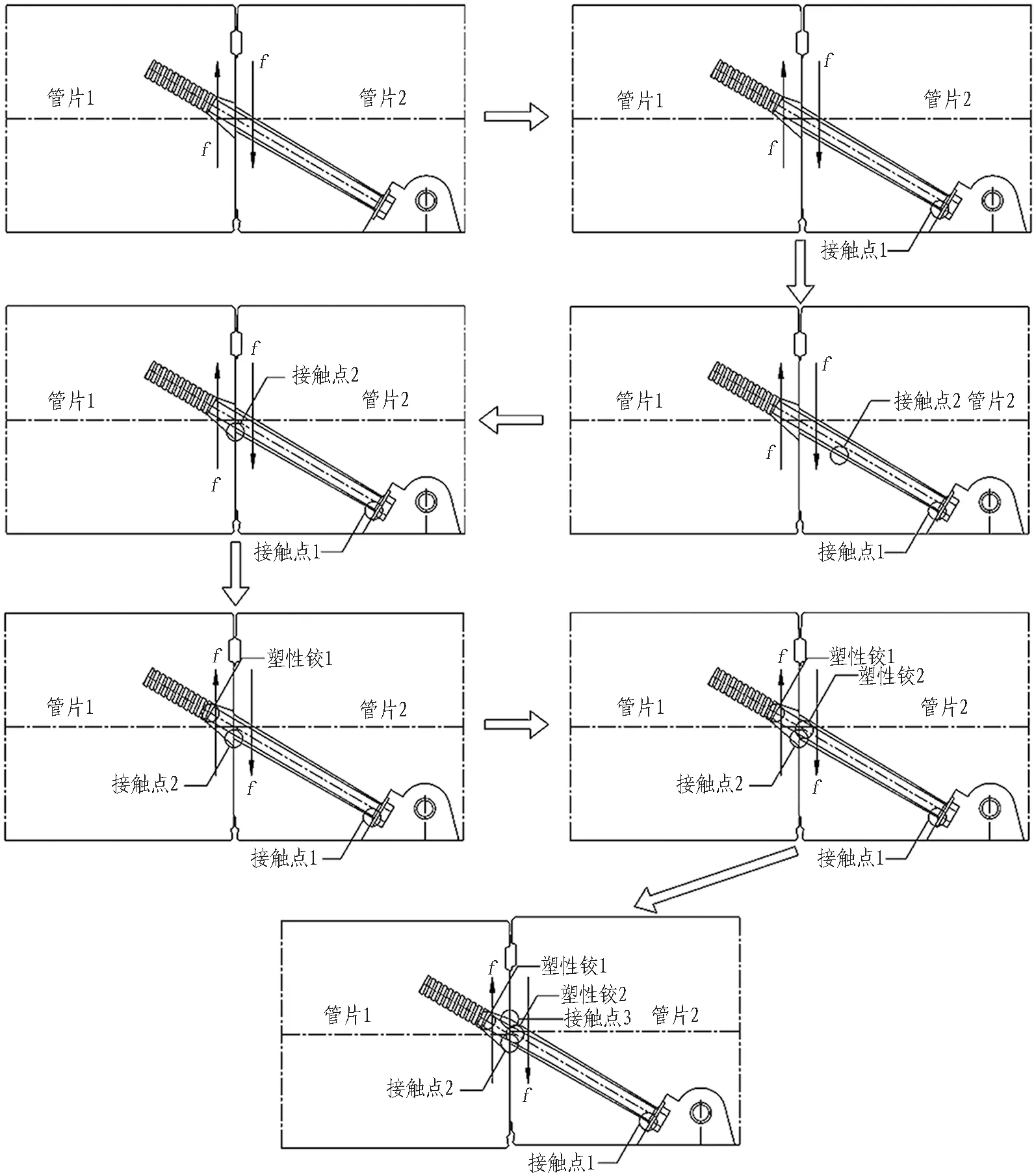
圖8 錨固端相對向下錯動環縫破壞過程示意圖

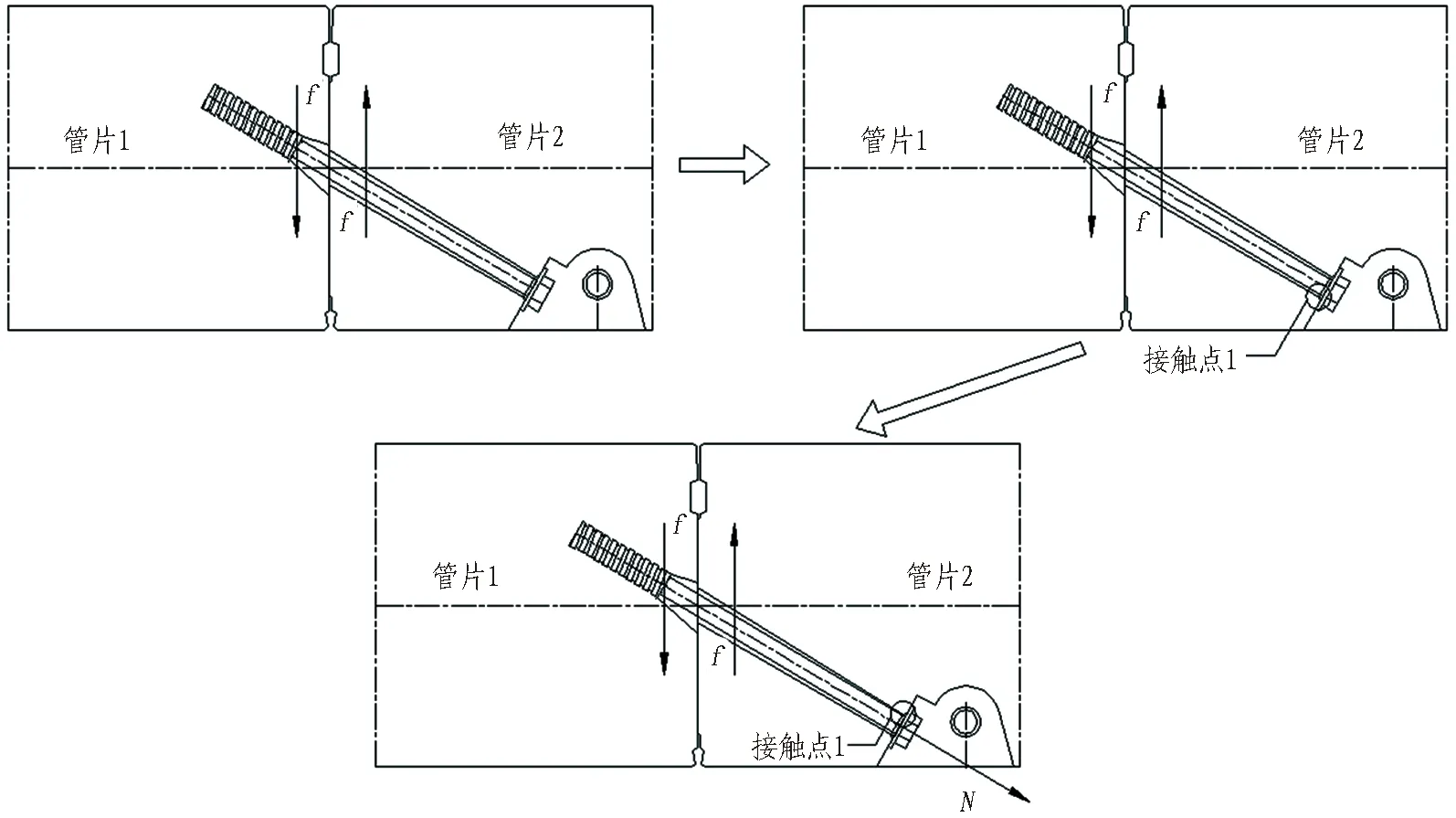
圖9 錨固端相對向上錯動環縫破壞過程示意圖

2.3 斜螺栓破壞過程詳解

環縫破壞的第1階段和第2階段其受力狀態都是比較清晰的；但在第3階段，由于斜螺栓的受力狀態十分復雜，且隨錯臺的發展不斷變化，有必要對其進行詳細分析。以下為便于描述，將第3階段的第1階段記為環縫破壞過程階段3.1，將第3階段的第2階段記為環縫破壞過程階段3.2，依此類推。

2.3.1 錨固端相對活動端向下錯動斜螺栓受力分析

2.3.1.1 線彈性階段斜螺栓受力分析

由于螺牙與套筒咬合良好，螺牙和光滑螺桿的交界點可以被視為固定端約束。在環縫破壞第2階段，斜螺栓已經與螺栓孔在螺母附近產生了接觸點1，接觸點1也可被視為固定支座。斜螺栓受力變形進入第3.1階段，其受力簡圖和彎矩圖如圖10所示。

(a) 第3.1階段邊界條件

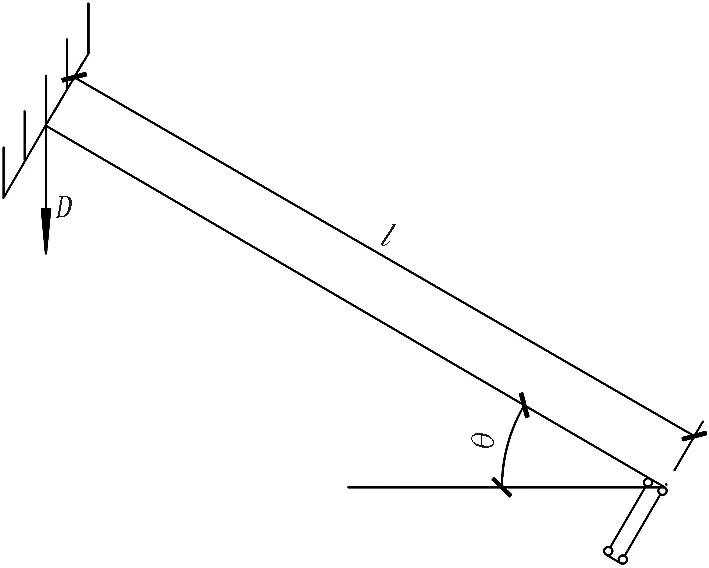
(b) 第3.1階段受力簡圖

(c) 第3.1階段彎矩圖

由結構力學的基本原理可知，第3.1階段的彎矩M的表達式如式(1)所示。

(1)

D′=Dcosθ。

(2)

式(1)—(2)中：EI為螺栓的截面抗彎剛度；θ為斜螺栓與水平方向的夾角；l為螺母端到螺牙和螺桿光滑段的交界點的距離；D為環縫破壞第3階段新產生的環縫錯臺；D′為D在Y方向的分量。

依據材料力學基本原理，彎矩是撓度的二階導數，結合階段1斜螺栓兩端固定的邊界條件，可以求得斜螺栓的撓度

(3)

螺栓孔的邊緣是一條直線，令該直線在坐標系中的表達式為

(4)

式中: -b/l為該直線的斜率；t為該直線在Y軸上的截距。

令螺栓變形過程中螺栓孔邊緣與斜螺栓邊緣的距離

ΔY=Y1-Y2。

(5)

對ΔY求導，可得

(6)

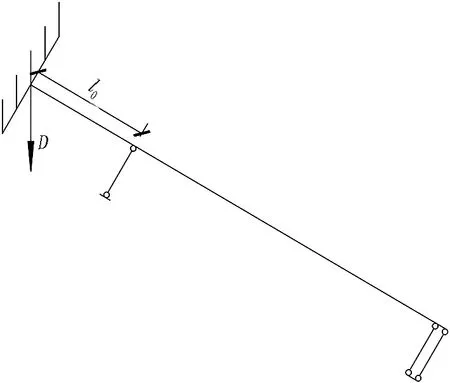
令ΔY′=0,求得ΔY的極小值點為X=l0。可知，在斜螺栓受力變形的過程中，X=l0處螺栓距離螺栓孔最近，隨著環縫錯臺D的不斷增加，該點是整條斜螺栓上首先接觸到螺栓孔的點。令ΔY(l0)=0，解得D′=D1cosθ。此時在X=l0處螺栓已經與螺栓孔相接觸。相當于在螺桿中部產生了一個新的支點接觸點2，接觸點2與固定端之間的距離為l0。斜螺栓受力變形進入第3.2階段，其受力簡圖和彎矩圖如圖11所示。

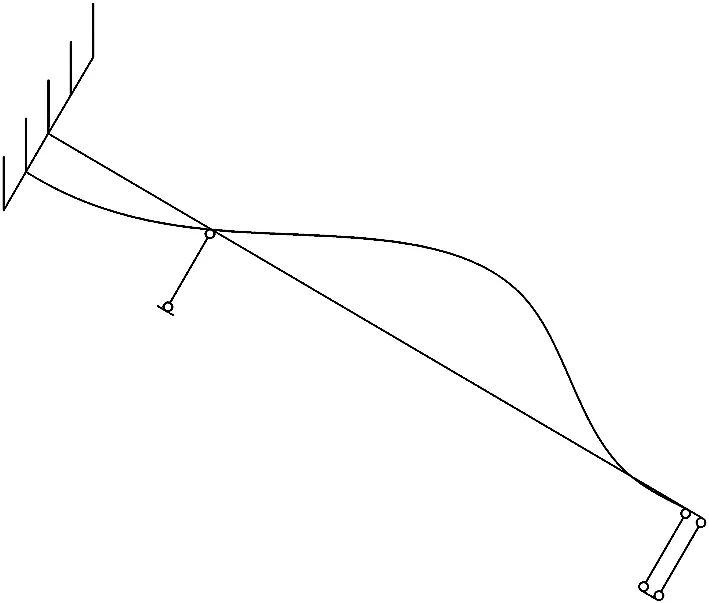
值得指出的是，至此整根螺桿尚處于線彈性狀態，可以采用結構力學中的疊加法思想，先獨立計算每一階段的內力和變形，然后再依據需要進行疊加。由結構力學的基本原理可知，不計第3.1階段產生的變形，第3.2階段螺桿的變形如圖11所示。可知： 第3.2階段的變形，使得支點左側螺桿產生向下的位移及支點右側螺桿產生向上的位移。可以預見，支點隨著環縫錯臺的發展將會逐漸向左移動。當支點運動到環縫處時，由于左側螺栓孔的直徑顯著大于右側螺栓孔，這一運動過程結束。運動過程結束時，支點位于環縫斷面附近，將此狀態視為螺栓受力變形第3.2階段的終點。假定第3.2階段結束時，第3.2階段產生的環縫錯臺增量為D2。

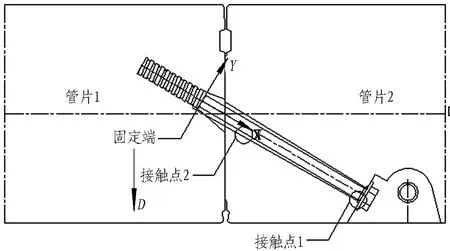
(a) 第3.2階段邊界條件

(b) 第3.2階段受力簡圖

(c) 第3.2階段變形圖

可以預見，由于斜螺栓的跨中支點在整個第3.2階段其位置不斷左移，因此整個第3.2階段環縫的抗剪剛度也在不斷增大。如圖12所示，設環縫斷面與斜螺栓軸線的交點和錨固端之間的距離為l′，則第3.2階段初始環縫抗剪剛度K20和第3.2階段最終環縫抗剪剛度K21如式(7)—(8)所示。

(7)

(8)

當斜螺栓的跨中支點移動到環縫與斜螺栓的交界點時，斜螺栓的受力變形進入第3.3階段，其受力簡圖和彎矩圖如圖12所示。

(a) 第3.3階段邊界條件

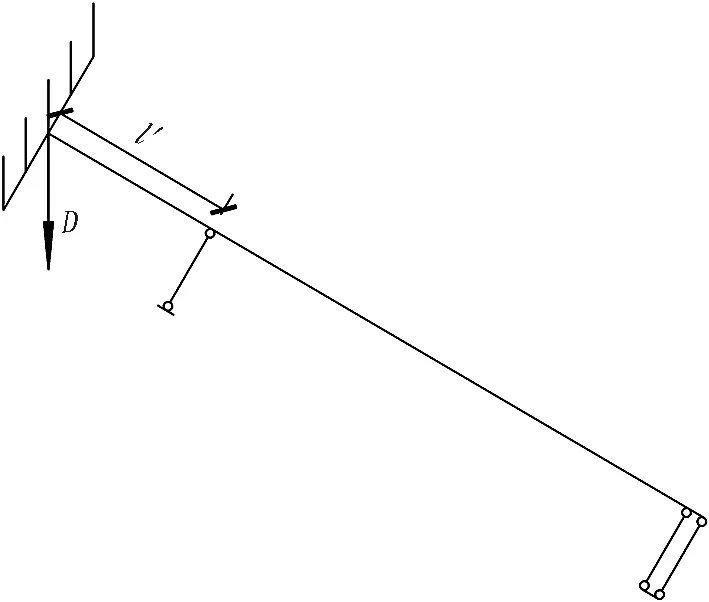
(b) 第3.3階段受力簡圖

(c) 第3.3階段彎矩圖

2.3.1.2 塑性鉸產生后的斜螺栓受力分析

在斜螺栓受力變形的第3.1、3.2、3.3階段，由于斜螺栓和螺栓孔之間的間距較小，斜螺栓處于線彈性狀態。但是，隨著環縫錯臺的進一步發展，斜螺栓上某些位置將產生塑性鉸。美國AISC-LRFD規范[14]認為，當截面的內力滿足式(9)—(10)要求時可以認為該截面位置已經形成了塑性鉸。

(9)

(10)

式(9)—(10)中：p為螺栓截面上的軸力；M為螺栓截面上的彎矩；py為截面的極限軸力;Mp為截面的塑性彎矩。

對于本研究而言，第3.1、3.2、3.3階段斷面上基本沒有軸力，橫截面塑性強度就是截面塑性極限彎矩Mp。

由第3.1、3.2、3.3階段的彎矩圖可知，3個階段彎矩疊加的結果是X=0處彎矩最大，此處為第1個塑性鉸出現的位置。假定第1個塑性鉸出現時環縫第3.3階段的錯臺達到D3，則由結構力學的基本原理可知，D3可通過式(11)求解。

D2cosθ=Mp。

(11)

此處將第3.2階段的剛度取為第3.2階段結束時剛度和第3.2階段初始時剛度的平均值。

當X=0處形成塑性鉸后，斜螺栓的受力簡圖再次發生變化，斜螺栓的受力變形進入第3.4階段，其受力簡圖和彎矩圖如圖13所示。

(a) 第3.4階段邊界條件

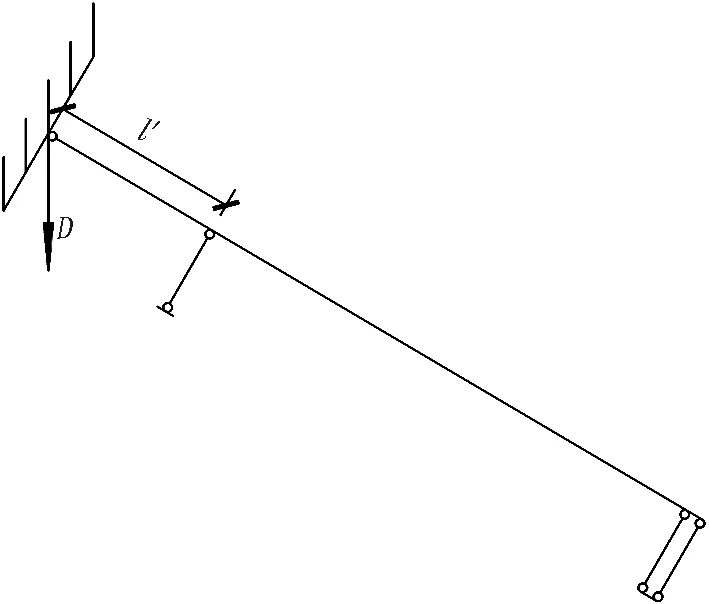
(b) 第3.4階段受力簡圖

(c) 第3.4階段彎矩圖

由于塑性鉸本身的受力特性不同于理想鉸，其不能夠自由轉動，塑性鉸產生后第3.1、3.2、3.3階段產生的內力仍然存在于螺桿各截面，此時螺桿截面的內力等于第3.4階段新增的內力與第3.1、3.2、3.3階段內力之和。

由第3.4階段的彎矩圖可知，斜螺栓跨中支點處(X=l′)的彎矩最大。由于第3.1、3.2、3.3階段X=0附近的彎矩遠大于其余位置彎矩，第1個塑性鉸形成時距離該塑性鉸較遠的斜螺栓橫截面上只具有較小的彎矩。第2個塑性鉸出現的主要原因是第3.4階段的新增彎矩，而非第3.1、3.2、3.3階段的彎矩累積。綜上所述，第2個塑性鉸將出現在斜螺栓跨中接觸點2附近。設第2個塑性鉸出現時第3.4階段的環縫錯臺為D4，則D4應滿足式(12)的要求。

(12)

此處將第2階段的剛度取為第3.2階段結束時的剛度K21，會造成計算出的內力值較實際內力偏大，這是一種偏于保守的做法。主要是考慮到此時斜螺栓上已經形成了2個塑性鉸，處于十分不穩定的狀態。

第2個塑性鉸出現時，斜螺栓的受力變形進入了第3.5階段，此時斜螺栓的受力簡圖如圖14所示。可知，由于第3.5階段整條斜螺栓上已經形成了2個塑性鉸，斜螺栓不再具有抵抗環縫錯臺的能力，斜螺栓將發生大變形。在這一變形過程中，雖然環縫錯臺很大，但是由于斜螺栓此時抵抗環縫錯臺的剛度喪失，在斜螺栓任意截面上不會有新的彎矩產生。但另一方面，由于斜螺栓產生大變形，因為此變形而產生的螺桿伸長量無法忽略，故而會在斷面上形成較大的軸力。假定某處于第3.5階段的斜螺栓，其連接的環縫在第3階段的總錯臺為D，則螺桿的軸力如圖14所示，螺桿上作用的軸力可按照式(13)計算。

(13)

式中:N為螺栓軸力；EA為斜螺栓的抗拉剛度。

抗拉強度較低的斜螺栓將在軸力N的作用下發生斷裂。對于在軸力N作用下不會斷裂的高強螺栓，大變形最終的結果為圖7所示左側螺栓孔上邊緣B點向下錯動后與螺桿接觸，形成新的支點。支點C和支點B之間很短的一段螺桿處于近乎純剪的受力狀態，最終斜螺栓在切應力和正應力的共同作用下發生破壞。此過程可以視為斜螺栓受力變形的第3.6階段。

(a) 第3.5階段邊界條件

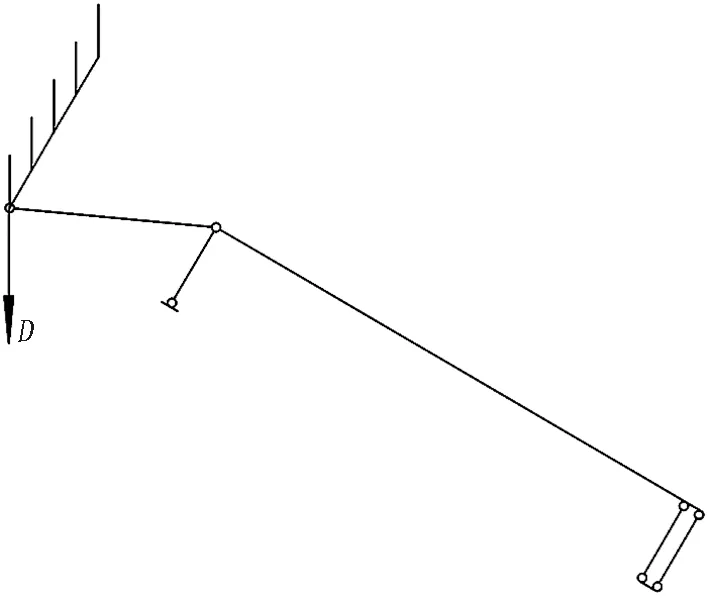
(b) 第3.5階段受力簡圖

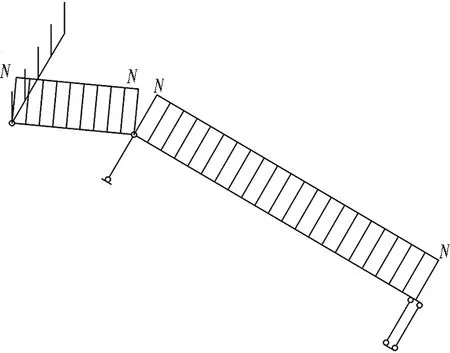
(c) 第3.5階段彎矩圖

2.3.2 錨固端相對活動端向上錯動斜螺栓受力分析

當錨固端相對于活動端向上錯動時，除彎矩外，斜螺栓各斷面還將產生附加軸力。計算結果表明，微小的錯臺即可引起很大的附加軸力。通常，在第2個接觸點產生之前，斜螺栓就已經屈服。因此，錨固端相對于活動端向上錯動的環縫，其破壞過程的第3階段環縫抗剪剛度不變。第3階段新增的斜螺栓軸力ΔN與第3階段新增錯臺D的關系如式(14)所示。錨固端相對于活動端向上錯動時斜螺栓環縫抗剪剛度K′在第3階段中的取值可按照 式(15)計算。

(14)

(15)

2.4 環縫破壞過程小結

綜合以上分析，理論上環縫破壞過程各階段抗剪剛度如表1所示。其中，K表示單根斜螺栓連接的環縫錨固端相對于活動端向下錯動的環縫剛度，K′表示單根斜螺栓連接的環縫錨固端相對于活動端向上錯動的環縫剛度。除剛度外，還需給出環縫破壞的判定依據。工程界普遍認為，當結構受到的荷載幾乎沒有增長，而變形持續發展時，可判定結構發生了破壞。具體到盾構隧道環縫，當環縫剪力幾乎沒有增長而環縫錯臺不斷發展時，判定環縫破壞。不難看出，依據此標準，對于錨固端相對于活動端向上錯動的環縫，斜螺栓受拉屈服時可以判定環縫發生破壞。對于錨固端相對于活動端向下錯動的環縫，當斜螺栓上出現第2個塑性鉸時可以判定環縫發生破壞。

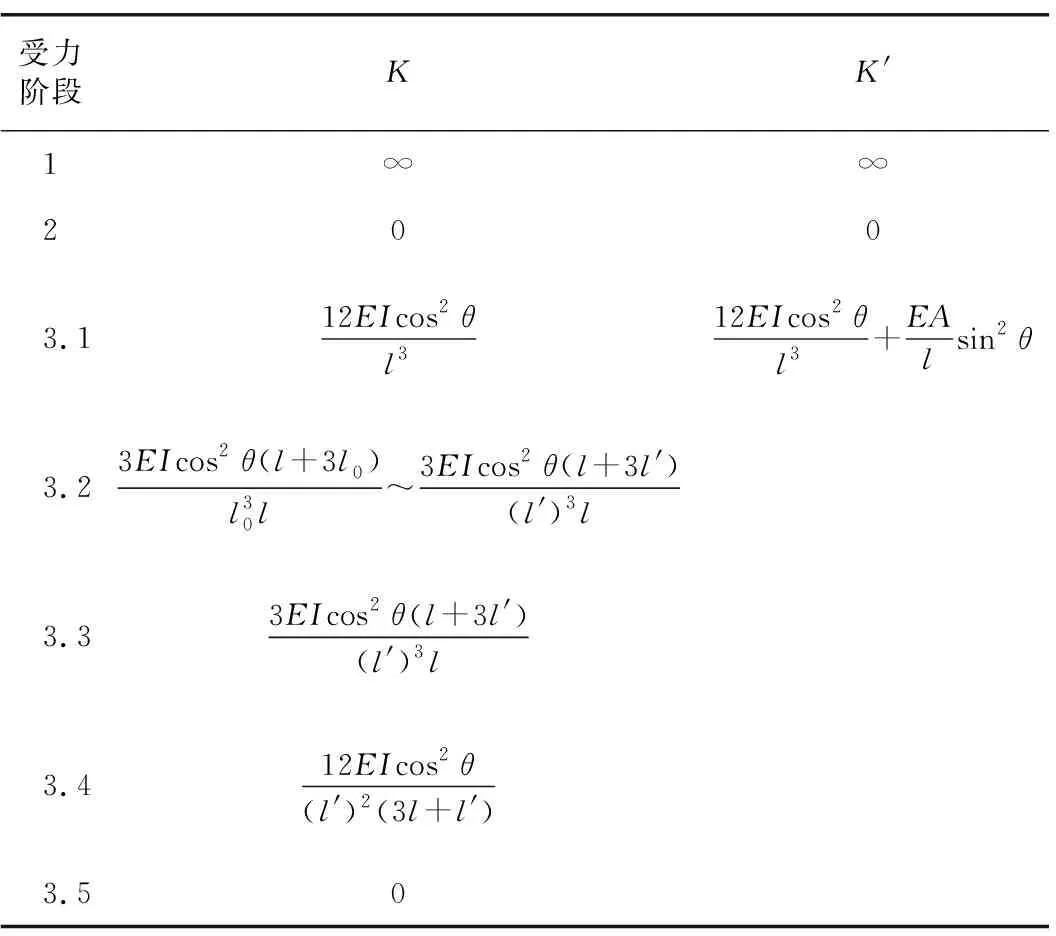
表1 環縫抗剪剛度表

2.5 試驗結果與解析解的對比分析

2.5.1 環縫剛度解析結果

對照第1.5節中的試驗結果，其與解析解在定性上是相符的。本節定量分析解析解與試驗結果之間的異同及其原因，以進一步驗證解析解的準確性。由圖2可知，環縫1錨固端相對于活動端向上錯動，環縫2錨固端相對于活動端向下錯動。將圖1所示環縫的細部尺寸帶入第2節所述各公式中，解得環縫2剛度變化規律如表2所示，環縫1剛度變化規律如表3所示。其中，D總表示環縫第1、2、3階段的總錯臺。F表示環縫剪力。由圖1可知： 1)試驗構件的環縫由2根斜螺栓連接，進入第3階段后，環縫2的實際抗剪剛度為2K； 2)試驗構件的環縫由2根斜螺栓連接，進入第3階段后環縫1的實際抗剪剛度為2K′。

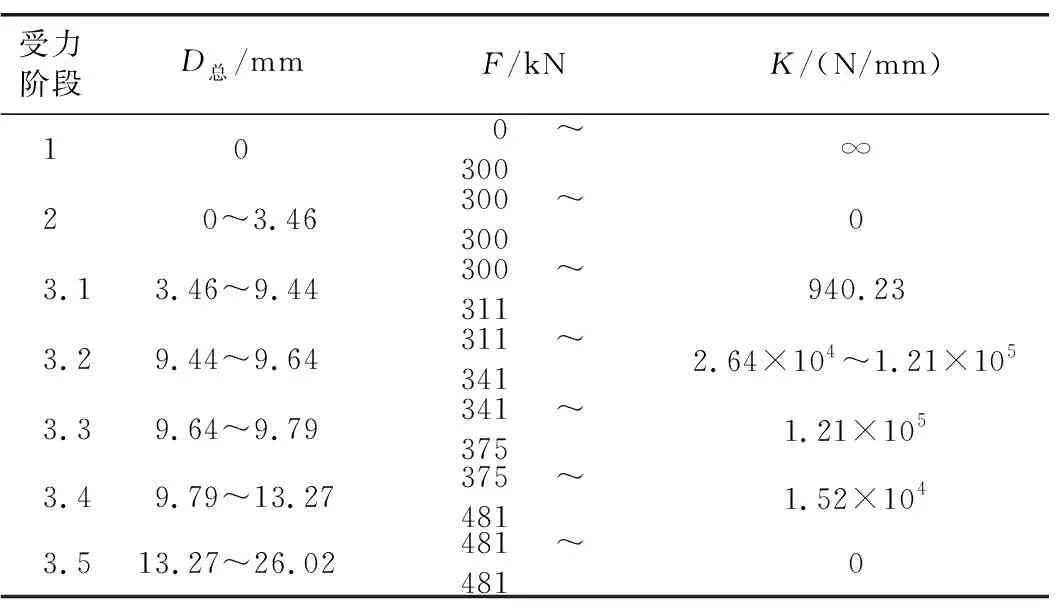
表2 環縫2剛度變化表

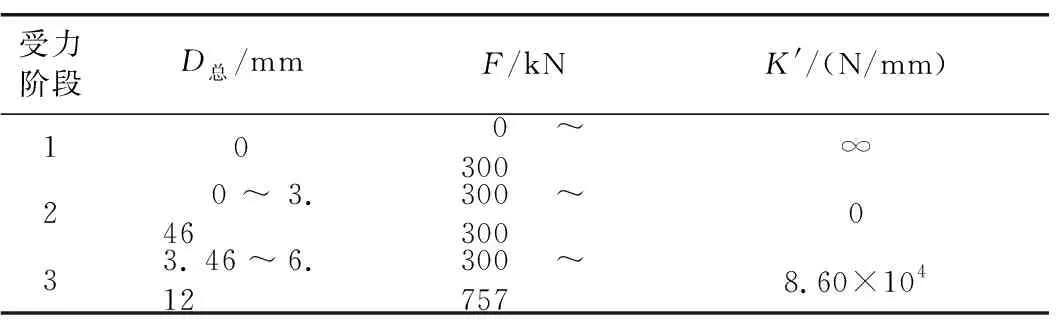
表3 環縫1剛度變化表

2.5.2 環縫2解析解與試驗結果比較

在同一個坐標系中描述環縫2理論環縫剪力-環縫錯臺關系與實測環縫剪力-環縫錯臺關系，如圖15所示。

圖15 環縫2錯臺實測值與理論值關系圖

由圖15可知： 于環縫2而言，實測環縫錯臺-環縫剪力曲線和理論環縫錯臺-環縫剪力曲線具有相同的變化趨勢。具體分析如下：

1)當環縫剪力為0～300 kN時(階段1)，環縫剪力主要由摩擦力承擔，環縫錯臺幾乎沒有發展，不論對理論值還是實測值均是如此。

2)當環縫剪力為300 kN時(階段2)，理論環縫錯臺-環縫剪力曲線出現水平段，這主要是由于斜螺栓活動端與螺栓孔之間存在3 mm的空隙。在此階段，實際環縫錯臺-環縫剪力曲線斜率很小，近乎水平。這表明在階段2理論環縫錯臺-環縫剪力曲線與實測環縫錯臺-環縫剪力曲線具有一致性。本階段實測環縫剪力-環縫錯臺曲線之所以具有很小的斜率，主要是由于螺母與螺栓孔端面具有一定大小的摩擦力，如圖16所示。理論模型中未考慮此影響因素。

3)當環縫剪力為300～311.24 kN時(階段3.1)，實測環縫剪力-環縫錯臺曲線與理論環縫剪力-環縫錯臺曲線具有相同的斜率，但此階段在相同環縫剪力作用下，理論值的錯臺均要比實測值稍大。這主要是由于，每一級荷載作用下的理論錯臺等于試驗中該級荷載作用下試驗構件錯臺發展完全穩定后的錯臺值。而在試驗過程中，由于目前沒有相關標準判斷環縫錯臺何時達到完全穩定，常采用的做法是當環縫錯臺發展速度很緩慢時開始施加下一級荷載。每級荷載造成的誤差會在環縫錯臺-環縫剪力曲線上累積，從而造成多個加載步以后，理論錯臺較實測錯臺稍有偏大的情況。

圖16 螺母與螺栓孔端面摩擦力

4)當環縫剪力為311.24～341.36 kN時(階段3.2)，理論環縫錯臺-環縫剪力曲線與實測環縫錯臺-環縫剪力曲線具有良好的一致性。

5)當環縫剪力為341～375 kN時(階段3.3)，實測環縫錯臺-環縫剪力曲線斜率小于理論環縫錯臺-環縫剪力曲線，這表明實測環縫剛度小于理論環縫剛度。這種現象產生的原因，主要是理論推導的過程中假定螺栓孔鋼筋混凝土完全不會破壞，而試驗過程中螺栓孔附近鋼筋混凝土雖然不會先于斜螺栓喪失承載能力，卻不免會產生一定的局部破壞，從而造成斜螺栓的活動空間增大，并由此導致環縫錯臺大于理論值、環縫剛度小于理論值的后果。螺栓孔位置發生的混凝土局部破壞如圖17所示。

圖17 螺栓孔附近局部破壞

6)當環縫剪力為375～481 kN時(階段3.4)，實測環縫剛度比理論環縫剛度稍小。其原因同樣是螺栓孔附近混凝土發生局部破壞。值得指出的是，在環縫剪力達到425 kN時，實測環縫錯臺-環縫剪力曲線進入了一段較短的平臺段。主要是由于斜螺栓跨中支點位置的混凝土發生了局部破壞，造成斜螺栓在無支撐的條件下快速向下錯動，直至接觸到未破壞的混凝土或螺旋筋，才恢復抗剪剛度。理論求得右側環縫的抗剪承載力為481 kN，實測右側環縫抗剪承載力為500 kN，二者相差4%，具有良好的一致性。

2.5.3 環縫1解析解與試驗結果比較

在同一個坐標系中描述環縫1理論和實測環縫剪力-環縫錯臺曲線，結果如圖18所示。具體分析如下：

1)環縫剪力為0～300 kN時(階段1)，理論上環縫錯臺沒有發展，環縫剛度為無窮大。實測環縫錯臺幾乎沒有發展，實測環縫剛度接近無窮大。極小的(約0.6 mm)的環縫錯臺是由于實際摩擦力與理想化的靜摩擦力有一定的區別。二者具有良好的匹配性。

2)當環縫剪力為300 kN時(階段2)，理論環縫剛度為0，實測值表明環縫此時尚具有較小的剛度，這主要是由于螺母墊片和螺栓孔端面的摩擦力。這種趨勢相比于右側環縫更加明顯，這是由于左側環縫屬于錨固端向上錯動的環縫，其螺母墊片與螺栓孔端面之間的正壓力更大，從而造成其間摩擦力更大。

3)當環縫剪力大于300 kN時(階段3)，環縫理論剛度稍大于環縫實測剛度，這可能是由于螺栓孔附近混凝土的局部破壞。

由于本次試驗所采用的試驗構件的構造特殊，當環縫2發生破壞后將無法繼續進行加載，此時環縫1遠遠未達到其承載能力極限狀態，無法比較環縫1的理論強度和實測強度。

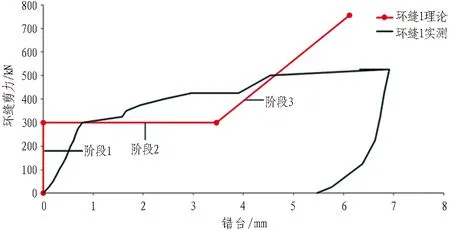
圖18 環縫1錯臺實測值與理論值關系圖

3 環縫剛度影響因素敏感性分析

由以上分析可知，盾構隧道環縫剛度的影響因素眾多，但是各因素對環縫剛度的影響大小不同。為找出對環縫剛度影響最大的因素，并在設計過程中對其加以控制，有必要對環縫剛度的各個影響因素進行敏感性分析。

絕大多數隧道環縫的錯臺較小，因此環縫的初期抗剪剛度最為重要。而由于第1階段抗剪剛度和第2階段抗剪剛度不受任何設計參數的影響，所以將第3.1階段抗剪剛度作為敏感性分析系統的輸出變量。由表1可知，第3.1階段環縫剛度受到斜螺栓傾斜角度、螺栓直徑、螺栓長度3個因素的影響，將此3因素視為系統的輸入變量。此處，將敏感性系數取為系統輸出變量對系統輸入變量的一階偏導數[15-16]。

由于各輸入變量單位和取值范圍均有不同，故首先對其進行歸一化處理。假定某一因素的變化范圍為(Xmin,Xmax)，則對該因素的某一取值X進行歸一化后的取值如式(16)所示。

(16)

經過歸一化后，輸入變量的取值范圍將統一變為(0,1)。

以下分析所采用的參數與第2節試驗中參數相同。

3.1 錨固端相對向上錯動環縫剛度影響因素分析

(17)

由式(17)可知： 對于錨固端相對向上錯動的環縫，環縫第3.1階段抗剪剛度隨斜螺栓與水平方向夾角的增加而增加，隨斜螺栓長度的增加而減小，隨斜螺栓直徑的增加而增加。其中，斜螺栓傾角對環縫剛度的影響大于斜螺栓直徑，斜螺栓直徑對環縫剛度的影響大于斜螺栓長度。

3.2 錨固端相對向下錯動環縫剛度影響因素分析

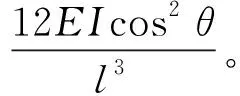
(18)

由式(18)可知： 對于錨固端相對向下錯動的環縫，第3.1階段的抗剪剛度隨斜螺栓與水平方向夾角的增加而減小，隨斜螺栓長度的增加而減小，隨斜螺栓直徑的增加而增加。其中對環縫抗剪剛度影響最大的是斜螺栓傾角，其次是斜螺栓長度，對環縫抗剪剛度影響最小的是斜螺栓直徑。

4 結論與建議

1)對于斜螺栓連接的無凹凸榫環縫，其剪切破壞過程分為3個階段，第1階段環間剪力由靜摩擦力平衡，環縫抗剪剛度無窮大； 第2階段在環縫剪力幾乎不增加的情況下錯臺有所發展，環縫抗剪剛度為0，主要是由于斜螺栓與螺栓孔之間的間隙； 第3階段環縫剪力增量由斜螺栓承擔，環縫抗剪剛度隨斜螺栓支撐條件以及塑性鉸產生過程而變化。

2)相鄰2環管片的相對運動方向會對第3階段環縫受力性能產生很大影響。螺栓錨固端所在管片環相對向上錯動時，第3階段環縫抗剪剛度基本不變，在破壞前一直維持在較高水平。螺栓錨固端所在管片環相對向下錯動時，第3階段抗剪剛度經歷了先增加、后減小、再增加的復雜變化過程。相比較而言，錨固端向上錯動的環縫具有更大的抗剪剛度，錨固端向下錯動的環縫具有較好的變形能力。

3)螺栓錨固端所在管片環相對向上錯動時，斜螺栓以受拉為主，環縫最終破壞原因是斜螺栓受拉屈服； 螺栓錨固端所在管片環相對向下錯動時，斜螺栓以受彎為主，環縫最終破壞原因是斜螺栓上產生2個塑性鉸從而喪失抗彎剛度。

4)對于錨固端相對向上錯動的環縫，環縫剛度最主要的影響因素是斜螺栓與水平方向的夾角，其次是斜螺栓直徑，再次是斜螺栓長度。對于錨固端相對向下錯動的環縫，環縫剛度最主要的影響因素是斜螺栓與水平方向的夾角，其次是斜螺栓長度，再次是斜螺栓直徑。

通過對以上結論的分析，建議在設計中通過調整斜螺栓與水平方向的夾角，以獲取所需的環縫剛度。