基于深度學習的雷達反射率外推評價的研究

柴文濤 羅飛 文立玉

(成都信息工程大學,四川成都 610225)

0 引言

隨著計算機技術的發展,目前,人工智能廣泛地應用于各個行業,在天文氣象領域也有重要的運用。以前預測天氣僅能依靠人工根據相關氣象知識進行預報,后來有各種氣象數值系統幫助人工更加準確預報,但其還是有局限性。隨著人工智能的發展,我們可以使用人工神經網絡來進行預測,其成本更低、精確度更高,其輔助人工預測、分析使得相關氣象人員能做出更快速、正確的決策。準確進行天氣預報能夠更好地服務民生、當地經濟,為減災防洪工作做出積極地響應。

1 雷達基本反射率

雷達反射率是空間單位體積中的大氣物質對雷達發射的微波的總后向散射截面。一般地說,它的值越大降雨、降雪的可能性越大,強度也越強,當它的值大于或等于40dbz 時,出現雷雨天氣的可能性較大;當它的值在45dbz或以上時,出現暴雨、冰雹、大風等強對流天氣的可能性較大。雷達基本反射率是一個重要的判別因子,因此對它的討論是必不可少的,很多重要的氣象要素都會結合基本反射率來研究。

2 雷達基本反射率的外推

外推法[1](Extrapolation)是根據某事物過去和現在的發展趨勢,來推斷或預測未來的一類方法的總稱,其用于科技、經濟和社會發展的預測,是情報研究法體系的重要部分。關于外推法,還有如下的相關解釋。比如:外推法是利用過去和現在已知其構成規律的動態統計數列向未來的延伸的方法。在定量分析中的外推法,主要是指時間序列預測法。這種方法的基本思路是把時間序列作為一隨機變量序列的一個樣本,應用概率統計的方法,盡可能減少偶然因素的影響,作出在統計意義上較好的預測。

定量分析中關于外推法的解釋更加契合本文的研究,因為本文的研究是基于雷達基本反射率數據,這種數據的典型特征是具有時間序列性,根據上述方法的基本思路,在時間維度上雷達反射率數據是連續的時間序列數據,將這樣連續的雷達序列數據作為一個樣本,使用相關神經網絡訓練模型,得到基于前序序列的雷達反射率數據的預測數據。

雷達反射率外推是指根據歷史雷達反射率值推測未來一段時間的反射率值,以此來推測未來一段時間某地區發生降雨、降雪等天氣現象。我們知道多普勒雷達掃射完成一次大約為6分鐘,因此雷達基本反射率的外推是根據歷史的前n個6分鐘數據,來推測未來n個6分鐘數據。

3 評價方案

3.1 均方誤差與結構相似性

對于圖像或者矩陣的評價,我們常使用均方誤差[2]和結構相似性來評價。均方誤差MSE(Mean Squared Error)是預測值與真實值之差的平方和的平均值,結構相似性SSIM(Structural Similarity Index)分別從亮度、對比度、結構三個方面衡量預測結果與真值間的距離。

其公式分別描述如下:

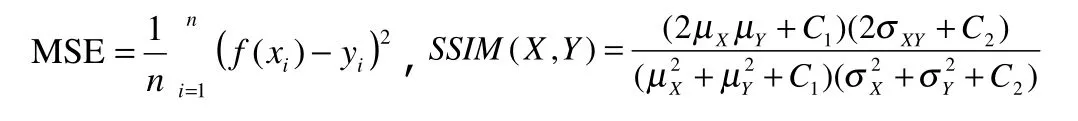
對于均方誤差MSE來說,f()一般為外推方法,即預測網絡,xi表示歷史數據,f(xi)表示預測的數據結果,yi表示真實的數據值。因此由公式可知道MSE 描述的是預測值與真實值的平方均值誤差。

對于結構相似性SSIM 來說,其中μX,μY,σX,σY,σ,σXY,C1,C2分別表示圖像X 的均值、圖像Y 的均值、圖像X的標準差、圖像Y的標準差、圖像X的方差、圖像Y的方差、圖像X和Y的協方差,C1和C2為常數,是為了避免分母為0而維持穩定,下面分別詳細的介紹這些量的公式及物理意義。下面分別討論亮度、對比度、結構三個方面的數學意義,首先對于離散信號,我們以平均灰度μx來作為亮度測量的估計,即求得基本反射率灰度圖像像素的平均值作為亮度值,其描述為:,其中N表示求其該反射率圖像上所有像素點。然后,由測量系統知道要把平均灰度值(亮度值)從信號當中去除,即對于每一個像素值都減去該圖像的平均灰度值,對于離散信號,可使用標準差來做對比度估量值,其描述為:,由對比度估量值σx,σy構成對比度函數c(x,y)。接下來,信號被自己的標準差相除,結構對比函數就被定義成和的函數。

在外推模型的訓練過程中,我們通常使用上述方法來定義相關的損失函數,但同時也可用它們作為評價方法。一般地,使用MSE 評價主要描述的是預測值與真實值的平方均值誤差,使用SSIM評價從宏觀上來看,其主要從圖像的結構上比較預測值與真實值間的距離。這兩種評價方式都有各自的優勢。

3.2 結合均方誤差和結構相似性的評價方法

我們結合均方誤差MSE 和結構相似性SSIM 提出新的評價方法,此評價方法即考慮圖像或者反射率值的平均誤差也關注圖像的結構特性,這里需要注意的是均方誤差MSE 的最好情況是結果為0,表示預測值和真實值之間完全一致,結構相似性SSIM 的最好情況是結果為1,表示預測值和真實值之間在結構、對比度和亮度方面的完全一致。為了整合公式在相同的比較規律上,我們將結構相似性的結果用1-SSIM 表示,即1-SSIM系統的最好情況是結果為0,這樣與MSE的最好情況相統一。

其中w1和w2分別是均方誤差和結構相似性的權重值,在設置w1和w2時,根據基本反射率數據的特性,具體描述如下:

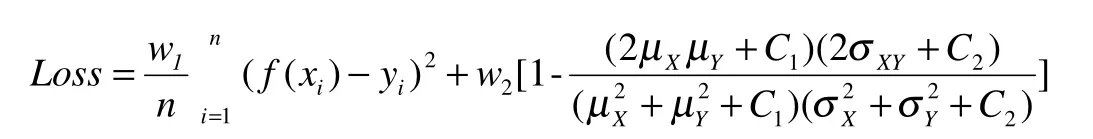
因此,我們使用Loss作為外推的評價,其在考慮均方誤差MSE的同時,也將結構相似性SSIM 作為一個評價成分。使用Loss評價是十分敏感的,這是因為即使MSE的達到最優,也不保證1-SSIM的值是最優的,要這兩者同時是最優的,即保證均方誤差較小的同時,其結構上也具有較小的誤差時Loss才是最小的,這樣的評價方法對外推質量提出了更高的要求,適合以圖像呈現結果時的基本反射率外推。

3.3 多尺度評價

所謂多尺度,實際上就是對信號的不同粒度的采樣,通常在不同的尺度下我們可以觀察到不同的特征,從而完成不同的任務。

對于結構相似性的多尺度技術MS-SSIM,其描述如下:

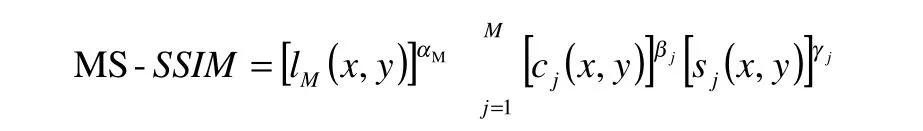
根據MS-SSIM論文[3]中的闡述假設有M個尺度,對于每個尺度來講αj=βj=γj,即每個尺度上的冪次權重相等,并且,這也就意味著,。對于明暗度lM()只使用最后一個尺度,因此不需要求累加它的權重。論文提出,在五個不同的尺度和十二個不同程度的變形上發現,當β1=?1=0.0448,β2=?2=0.2856,β3=?3=0.3001,β4=?4=0.2363,andα5=β5=?5=0.1333時,圖像的質量是不變的,因此將這五個參數值作為常量,使得MS-SSIM 的評價更為客觀。

不同尺度所計算得到預測值與真值的對比度和結構是不同的,因此多尺度結構相似性MS-SSIM 相較于SSIM對尺度更為敏感。文中也解釋了且用實驗驗證了僅使用均方誤差MSE的缺陷問題,文中相關實驗展示了5個尺度(行)和12個失真等級(列)構成的圖像矩陣(得到60幅圖像)。每個失真圖像都是使用迭代過程創建的,其中初始圖像是通過隨機向原始圖像添加高斯白噪聲來生成的,每一行的迭代過程是由一種約束梯度下降算法生成的。在約束均方誤差MSE 固定不變的同時,依據結構相似性算法SSIM搜索質量最壞的圖像,并限制失真僅發生在指定的尺度上。因此我們知道在同一行中,圖像相對于原始圖像具有相同的均方誤差MSE,但其視覺質量存在顯著差異。因此這些差異并不能通過均方誤差MSE 區分開,但因為尺度不同可以使用結構相似性區分開來。因此,不同尺度的失真在感知圖像質量方面具有非常不同的重要性。

因此,僅使用MSE是不完善的,這時引入MS-SSIM 就顯得很重要,因為MS-SSIM 在不同噪聲圖像上會得到不同的評價結果,雖然這些噪聲在MSE上是相同的評價。同樣地,使用1-MS-SSIM使得其在公式中判別方向與MSE一致,引入以下帶有均方誤差MSE 的多尺度結構相似性評價函數MSDM 如下:

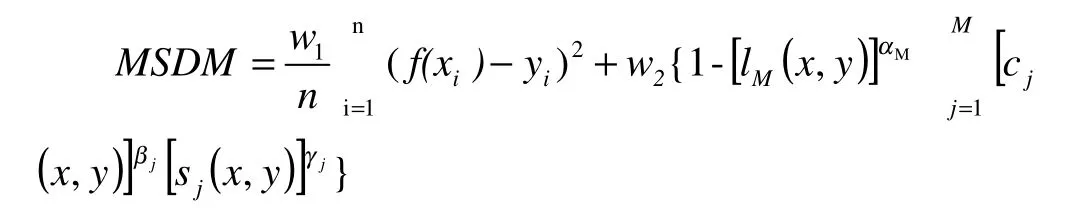
同樣地,本文設置w1=w2=0.5使得均方誤差和多尺度結構相似性同時均等有效,當出現噪聲等因素使得MSE失效時,MS-SSIM 會根據尺度特性評價其質量,從而使得評價結果更客觀有效。對于上述公式中的xi,yi,x,y其具體含義描述如下,讓x={xi|i=1,2,...,N},y={yi|i=1,2,...,N}這兩個離散非負信號相互一致,例如此處的分別從對應兩個圖像的空間位置上提取相同的像素或區域。

灰度圖像可以通過以下公式實現灰度和反射率值的相互轉化:

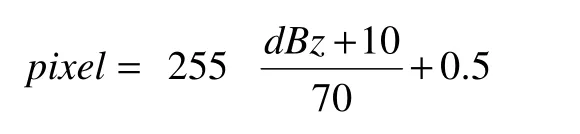
灰度圖像的噪聲或者因為尺度問題所導致的與真值差異體現在這些像素值pixel的差異上,將這些有差異的像素值轉換為反射率值dBz同樣會導致反射率值的改變,這樣往往會導致預測的反射率值不準確,因此MSDM評價能夠盡可能地找出預測值與真值間的差異,使得最后得出的反射率值盡可能準確或在更小的誤差范圍內。

在圖像上幾乎所有的質量問題(如放大縮小、噪聲等)都是因為改變了圖像的像素值,從上面的分析可以認為在某些情況下均方誤差MSE 對噪聲是不敏感的,而多尺度結構相似性MS-SSIM對噪聲可以因尺度的變化而變得敏感,因此使用多種評價方法使得其更加有效的評價圖像結果,使得評價更加客觀。與此同時,引入與評價函數同樣的損失函數可使得網絡訓練的更好。本文提出的MSDM 在這些性能上比單獨使用MSE 或者SSIM 或者MS-SSIM更好。

4 結語

本文討論了雷達反射率的外推評價,從雷達反射率和外推出發介紹了其物理意義,討論了常見的評價方法,即均方誤差和結構相似性。均方誤差MSE 是預測值與真實值之差的平方和的平均值,結構相似性SSIM分別從亮度、對比度、結構三個方面衡量預測結果與真值間的距離,多尺度MS-SSIM 是基于結構相似性SSIM,并且從多個尺度來衡量預測結果與真值間的距離。其中僅使用MSE 是不完善的,這時引入MS-SSIM就顯得很重要,因為MS-SSIM在不同噪聲圖像上會得到不同的評價結果,雖然這些噪聲在MSE 上是相同的評價。本文提出的MSDM評價方法,結合均方誤差和多尺度結構相似性,能夠盡可能地找出預測值與真值間的差異,使得最后得出的反射率值盡可能準確或在更小的誤差范圍內。提出的MSDM 評價方法結合了兩種基本評價方法,這些評價方法能夠從不同角度,更為客觀的、科學的評估外推的結果,對雷達外推有重要的意義。