一種基于機器學習的貧困家庭識別方法

詹中華，沈同平，金 力，黃方亮，許歡慶

國家各級部門為了確保貧困家庭的子女接受正常的教育，相繼頒布《教育部辦公廳關于進一步加強和規范高校家庭經濟困難學生認定工作的通知》和《教育部等六部門關于做好家庭經濟困難學生認定工作的指導意見》等文件，對新時期貧困生的認定工作作出了新的部署和要求［1].為了更好地做好“教育扶貧”和“教育救助”工作，高效、準確地識別家庭經濟困難學生，并及時給予政策資助，讓貧困學生能夠順利完成學業，提高學生資助效果，成為急需解決的問題之一.只有在精準識別貧困生的問題得到妥善解決以后，“精準資助”工作才能真正做到公平、公正、公開，利用有限的資金幫助那些家庭經濟真正困難的學生，達到“不讓一名學生因為家庭貧困而失學”的目的.

國家各級教育管理部門高度重視高等學校學生資助管理工作，不斷制定和頒布學生資助管理制度，學生資助工作成效卓著.但在學生資助和貧困生認定工作中，也存在一些問題.比如，目前高校貧困生等級的評定方式和方法比較簡單，缺乏足夠的客觀量化標準，容易夾雜評委的個人情感；貧困生認定過程中存在弄虛作假情況；貧困生認定過程中需要貧困生將家庭情況當眾說明，進行“比窮”“比困”和“比慘”，將貧困生家庭情況過度曝光，不利于保護個人隱私，甚至會傷害到貧困學生的自尊心.

為了提高學生資助管理工作的效率和效果，國內一些專家學者從不同角度對貧困生認定工作進行了研究，以期實現對貧困生的精準資助.李靜以高校助學金等級評定工作為研究對象，將采用裝袋（Bagging）集成方法的隨機森林模型應用于助學金等級預測中，并與分類回歸樹（CART）算法進行比較［2].謝穎等將HMM的Baum?welch算法應用到高校家庭貧困生認定過程中，將結果與直接計算方法及通過實際調研得到的結論進行對比，通過對比得到HMM算法在解決此類問題中存在的局限性，同時給出了提高預測準確性的新模型建立的建議［3].蔡炫在高校貧困生認定工作中引入家庭人力資源這個概念，有助于更好地分析和判斷學生家庭經濟情況，通過對家庭人力資源數量、類別和素質等方面進行分析，探索其運用于高校貧困生認定工作中的方法［4].苗興國認為，要想真正解決貧困生認定難問題，必須明確家庭經濟因素在這一認定體系中的基礎性作用，以及怎樣通過各種方式最真實地反映申請貧困學生的家庭經濟因素［5].在目前的高校助學金評定模型中，主要是通過對學生日常消費數據和圖書館借閱數據等進行分析，采用機器學習技術中的某一個模型進行分析和預測，缺乏模型對比分析，效果較差.貧困生是由學生家庭經濟狀況決定的，因此對貧困家庭的識別是貧困生等級評定的前提工作.文獻［4]和文獻［5]從家庭的角度出發，重點考慮家庭人力資源和家庭經濟狀況兩個指標對貧困生認定的影響，但沒有給出具體的量化標準和評定方法.

本文在分析目前高校貧困生評定工作的基礎上，結合高校精準資助研究成果，重點考慮學生家庭狀況與貧困的關系，以哥斯達黎加家庭貧困水平預測數據集為分析對象，進行探索性數據分析和處理，以機器學習方法為技術支撐，采用隨機森林、樸素貝葉斯、邏輯回歸等模型進行對比分析，構建精準識別貧困家庭模型.將機器學習技術融入貧困生認定工作中，可以減少主觀經驗判斷，實現精準資助，確保貧困學生在政策資助下，順利完成學業，阻斷貧困的代際傳遞.

1 機器學習相關理論

機器學習主要指計算機通過模擬或實現人類的學習行為，獲取相應知識和技能.學習過程是借助數據模型，對輸入的訓練數據進行分析和歸類，找出數據之間的規律，作為決策函數的參數和權重，并用該模型函數對輸入的未知數據進行預測和標記，常見的機器學習模型有決策樹、支持向量機、樸素貝葉斯和K近鄰等算法模型［6].在貧困生評定等級工作中，機器學習模型通過對貧困家庭數據的學習，對貧困等級進行預測.

1.1 支持向量機

支持向量機是機器學習模型中的一種二分類模型，根據間隔最大化的原則，在訓練集的各類樣本點中，尋找一個超平面對各類樣本進行分割，最終轉化為一個凸二次規劃問題進行求解.

分類決策函數：

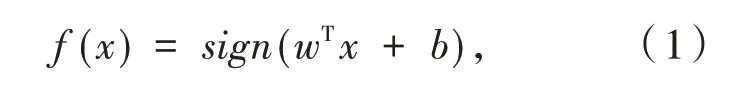
其中，sign(?)為階躍函數：

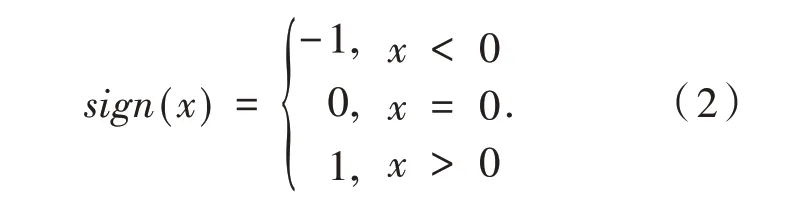
1.2 樸素貝葉斯

樸素貝葉斯分類是貝葉斯算法中最簡單的一種分類算法，對于待分類項，只需求解在此項出現的條件下各個類別出現的最大概率.樸素貝葉斯模型預先假設各屬性之間互相獨立，但在實際應用中，分類屬性之間存在一定的相關性，影響分類效果.

樸素貝葉斯計算公式：

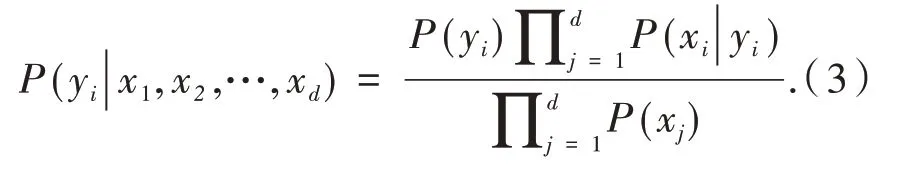
1.3 K近鄰

K近鄰是一種經典的數據挖掘分類算法，通過測量不同樣本之間的距離，對樣本進行分類.大體思想是計算給定樣本與其他樣本之間的距離，選出距離該樣本最近的K個鄰近值，如果這K個樣本大多屬于某個類別，則該樣本同屬于這一類別.根據K近鄰算法，對給定樣本x找出訓練集中與樣本x最近的全部K個樣本，記作Nk(x)，K近鄰計算公式：

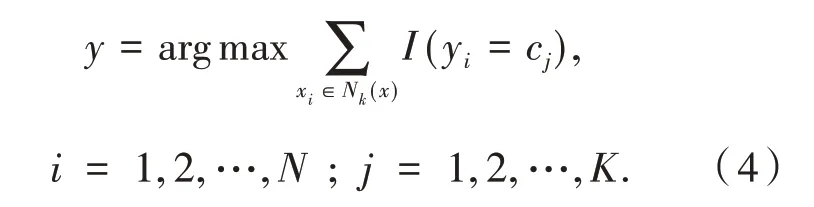
2 數據來源與分析

2.1 數據集介紹

本文研究數據來源于Kaggle網站上的哥斯達黎加家庭貧困水平預測數據集.根據模型需要，將數據集劃分為訓練集和測試集兩個部分.測試集共有7334個樣本數據，訓練集共有2973個樣本數據，每個樣本數據已經標注好貧困等級.家庭貧困程度分為四個等級，分別用數字1、2、3、4表示，1表示極度貧困（extreme poverty），2表示中等貧困（moderate poverty），3表示一般貧困（vulnerablehouseholds），4表示不貧困（non vulnerable households）.數據集中共有142個字段，部分字段和變量的含義如表1所示.

表1 數據集中部分屬性列表

該數據采用多個指標和維度對家庭貧困等級進行描述，包括家庭中男性和女性的數量、勞動力和非勞動力的統計、家庭成員的受教育水平、房屋面積和臥室數量的統計、房屋貸款情況統計、家庭成員健康情況統計、生活費用（供水、供電等）統計等142個屬性，這些屬性可以全面地對一個家庭的經濟狀況進行描述和確定.

2.2 數據集分析

哥斯達黎加家庭貧困水平預測數據集中，訓練集包含2973個貧困家庭樣本，如圖1所示.貧困等級為1的家庭數為222，貧困等級為2的家庭數為442，貧困等級為3的家庭數為355，貧困等級為4的家庭數為1954.

在現階段，每個家庭的貧困程度不同，極度貧困家庭數量相對較少.圖1顯示，貧困等級是4的樣本數與等級是1的樣本數的比例接近9∶1，表明訓練集的不同類別樣本數量是不均衡的.樣本不平衡率越大，數據集中類別不均衡程度越嚴重.傳統的分類方法偏向于多數的類，對于較少的類，執行的效果往往較差，在使用機器學習經典模型時，需要對訓練集的數據進行處理，提高模型預測準確度.

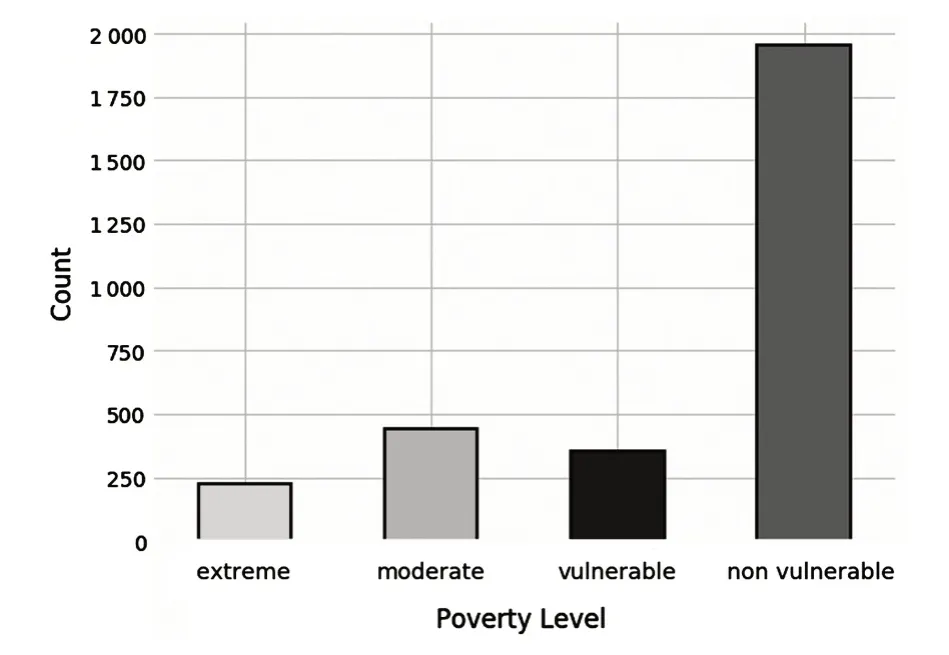
圖1 訓練集貧困等級數據分布

對訓練集中的數據進一步探索變量和貧困等級之間的關系.從圖2和圖3中，可以發現教育程度與家庭貧困情況存在直接的關系.家庭成員受教育程度越高，家庭貧困狀況越良好；家庭成員受教育平均程度越高，家庭貧困狀況越良好.

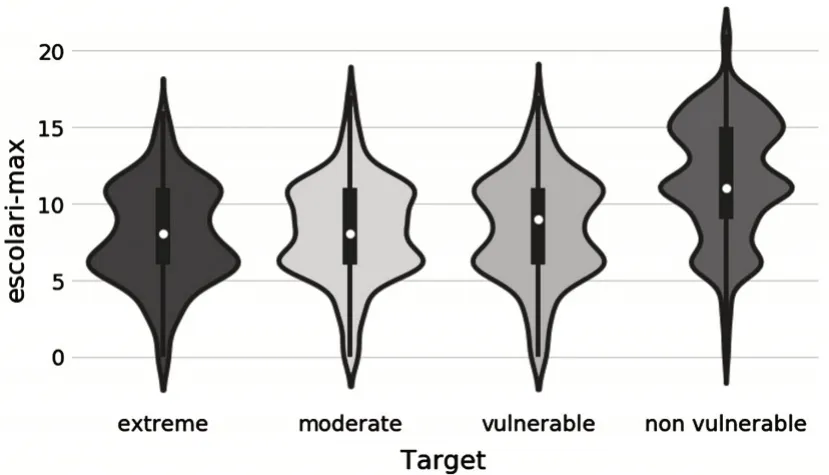
圖2 最高學歷與貧困等級的關系

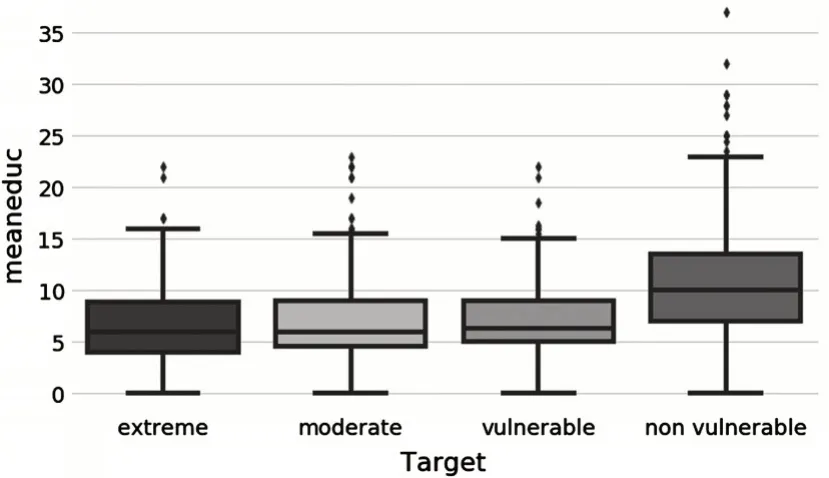
圖3 平均受教育程度與貧困等級的關系

探索女戶主以及女戶主家庭平均教育水平與貧困等級的關系，如圖4和圖5所示.從圖中可以發現，戶主是女性的家庭似乎更容易出現嚴重的貧困.從家庭教育水平的角度來看，女戶主家庭都具有較高的教育水平.

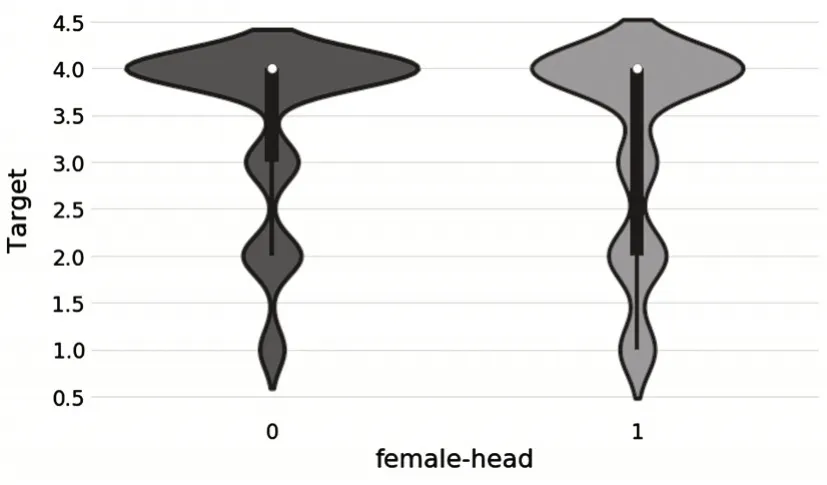
圖4 女戶主家庭與貧困等級的關系

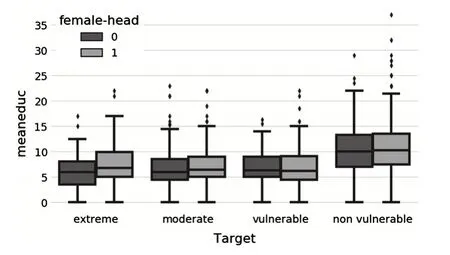
圖5 女戶主家庭平均教育水平與貧困等級的關系

受篇幅限制，文章僅對訓練集中的部分字段變量進行探索性分析，這些變量與貧困等級確定高度相關.這些變量是否真正有用，將通過后續模型進行驗證分析.

3 模型結果分析

實驗采用的環境為：

軟件環境：Windows7下的Tensor Flow 1.11.0版本；

硬件環境：Inteli5?4590 CPU 3.30 GHz；

內存：8.0 GB.

為了驗證本文模型的有效性，采用通過精確率（Precision）、召回率（Recall）、F1值和精確率（Accuracy）對模型評價.

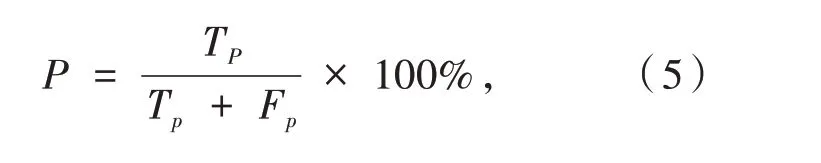
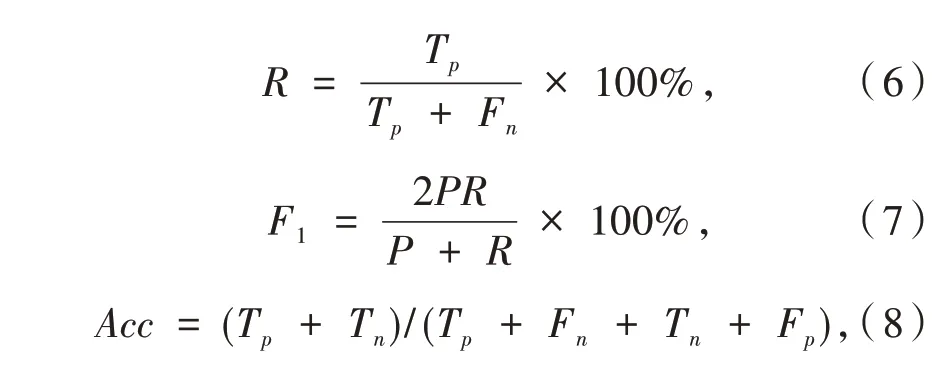
其中：Tp表示真正例，Fp表示假正例，Tn表示真負例，Fn表示假負例.

表2中的五種算法分別為，KNN（K近鄰算法）、LR（邏輯回歸算法）、NB（樸素貝葉斯算法）、SVC（支持向量機算法）、RF（隨機森林算法）.

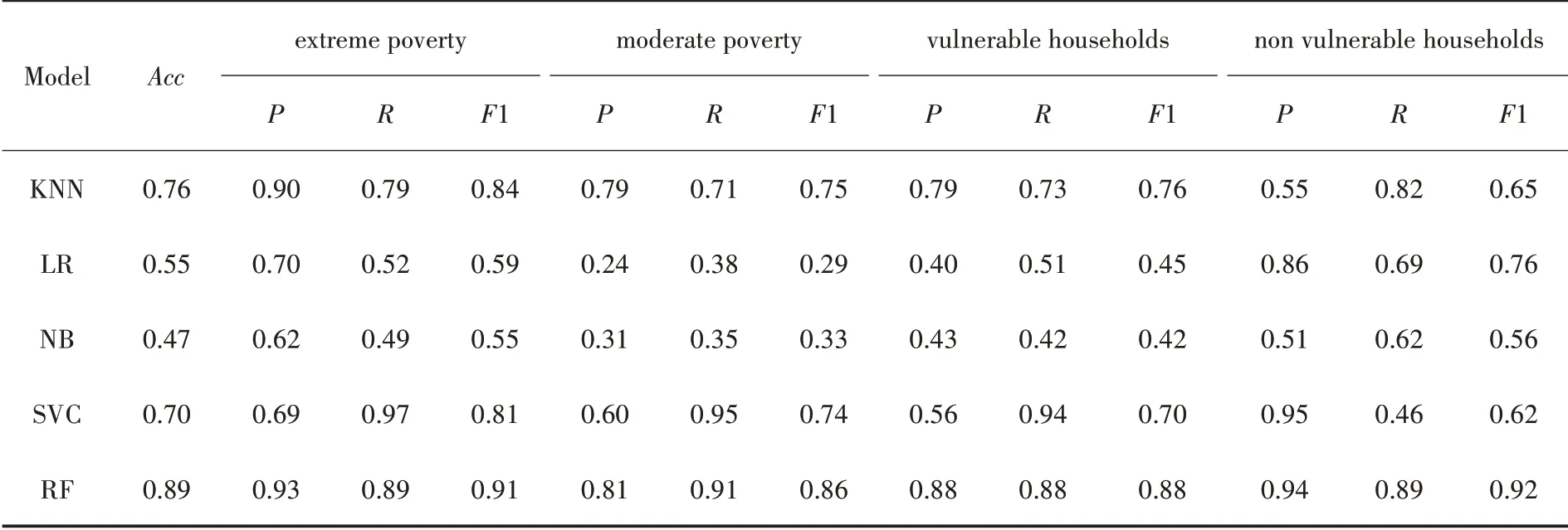
表2 五種分類算法的檢測結果

五種分類算法取得檢測結果不相同.隨機森林算法和K近鄰算法準確度較高，分別達到89%和76%；邏輯回歸和樸素貝葉斯算法準確度較低，分別為55%和47%.

不同分類算法對不同貧困等級的精確度、召回值和F1值都不相同.其中，隨機森林算法對extreme poverty等級數據，精確度最高；支持向量機算法對non vulnerable households等級數據，召回值最高，邏輯回歸算法對moder?ate poverty等級數據，精確度最低，僅為24%.

綜合表2中的數據，隨機森林算法綜合效果最好，樸素貝葉斯算法綜合效果最差.

4 結論

本文利用機器學習的方法，通過對貧困家庭數據的分析和學習，確定學生的家庭經濟狀況和貧困等級，避免申請學生當眾“比慘”現象的發生，有效保護了貧困學生的隱私.分別使用邏輯回歸、支持向量機、K近鄰、決策樹、隨機森林等機器學習算法進行貧困家庭識別.實驗結果表明，集成機器學習算法性能優于傳統機器學習算法，隨機森林算法的預測性能最佳，平均準確率為89%.本文研究結果可以作為高校貧困生評定工作中的一種重要參考和支撐.在對學生家庭經濟狀況數據的分析和預測過程中，本文的研究結果可以作為貧困生等級認定的一種參考，進而實現精準認定貧困生，實現以生為本的差異化精準資助新模式，提高高校資助管理工作的水平和效果.