基于初等因子法的線性代數復矩陣相似標準型研究

宋 永

線性代數復矩陣的運算在信號處理、雷達成像、人工智能、衛星通信等科技領域都具有重要作用，憑借著簡明、直觀的表達方式及穩定可靠的運算速度，已經成為現代工程技術中的重要數學求解工具［1].線性代數復矩陣求解的方式很多，包括分解、乘法和求逆，其中，線性代數復矩陣的相似標準型是解決這些問題的關鍵.國外對于基于初等因子法的線性代數復矩陣相似標準型研究通常采用Cholesky分解算法，上世紀末期，研究者基于Cholesky分解算法設計了一種線性代數復矩陣相似標準型存在性的研究方法，并對其進行了實驗驗證，Cholesky分解算法的運算量非常小，在應用過程中方便硬件的實現［2]；國內學者最初將QR分解算法應用到基于初等因子法的線性代數復矩陣相似標準型研究中，具有較高的并行度，在硬件設計中具有重要應用［3].

許成亮等人［4]根據線性代數變換相似性與復矩陣相似性之間的等價關系，利用任意域上位移算子與一般算子，推導出線性代數復矩陣中相似標準型的存在性，并將其推廣到任意域上，求出廣義意義上的相似標準型；梁海華等人［5]考慮到一類帶非負系數矩陣的復雜性，當矩陣線性增長時，會具有奇異性，利用矩陣的初等變換法建立了解的存在性充分條件，并給出實例來證明正解存在性的應用.

基于以上研究背景，本文研究了線性代數復矩陣的相似標準型存在性，以簡化線性代數復矩陣的求解過程.

1 優化線性代數復矩陣運算算法

針對高速、高并行、低資源消耗系統對線性代數復矩陣計算性能的要求［6]，對線性代數復矩陣的運算算法進行了研究與比較.將線性代數復矩陣運算算法直接應用到矩陣求解計算中，具有諸多缺點.在矩陣的QR分解算法中，存在許多復雜的計算過程，如平方根運算、除法運算等，而傳統的LU分解算法包含了大量的消元計算和迭代計算過程.用QR分解算法和LU分解算法的逆算法，首先對線性代數復矩陣進行分解運算，然后對分解后得到的兩個中間矩陣進行逆運算，最后將兩個逆矩陣相乘得到線性代數復矩陣的逆矩陣.線性代數復矩陣的全分解逆過程具有計算量大、中間的迭代操作多、并行度低、資源消耗高以及運行時間長的問題［7]，因此采用按位替換法來求解線性代數復矩陣.

假設存在線性代數復矩陣：

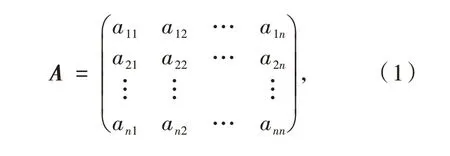
A表示所有主子式中不為0的n階方陣，aij為第i行、第j列的元素，其中i，j=1，2，3，…，n.依據按位替換法來求解線性代數復矩陣，先對待求解的線性代數復矩陣求解約化系數，得到線性代數復矩陣的n階方陣N，具體的計算過程為：

采用公式（2）得到約化系數n階方陣N的第1行第1列元素：

式中：i和j的取值從2開始，通常取正整數.

根據公式（3）得到約化系數n階方陣N的對角元素為：

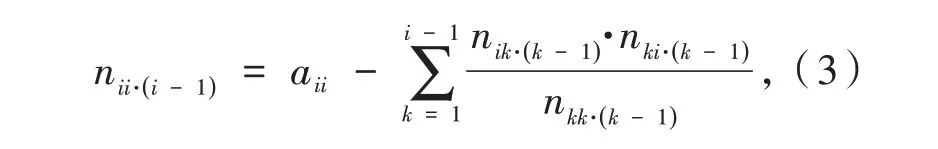
式中：k的取值為k=2，3，…，i?1，i的取值為i=2，3，…，m.

根據公式（4）計算約化系數n階方陣N的下三角元素為：

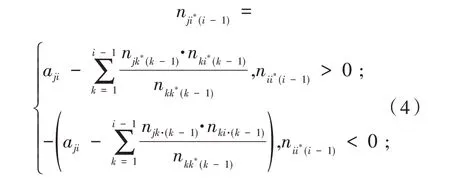
式中：i的取值為i=2，3，…，m?1，j的取值為j=i+1，i+2，…，m.

基于以上步驟，得到約化系數n階方陣N，表示為：

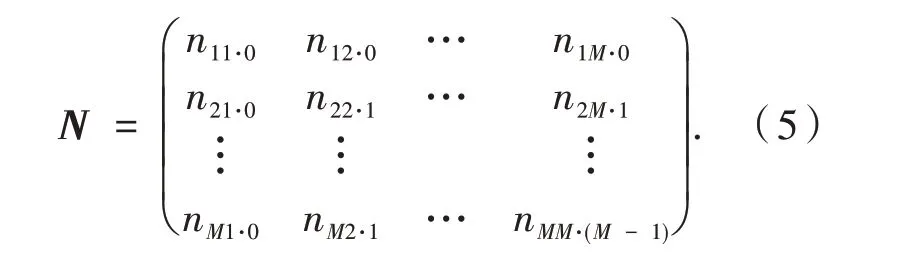
與線性代數復矩陣的傳統求解方法不同的是，按位替換法［8]計算出約化系數n階方陣N之后，可以直接求解出線性代數復矩陣A分解后的三角矩陣和上三角矩陣，最后將兩者相乘得到線性代數復矩陣A的解.

線性代數復矩陣的計算復雜度［9]是比較計算功耗與計算速度的重要指標.在算法的優化設計中，線性代數復矩陣的計算復雜度包括空間復雜度和時間復雜度.對于高性能運算算法的設計，關鍵在于根據算法應用的不同領域和應用平臺來改進運算算法，從而實現內容和體系結構的整體優化.評估線性代數復矩陣性能的一個重要指標應該是復矩陣本身的運行次數，運算量也可表示為線性代數復矩陣執行時間的長度，它與資源存取次數和邏輯切換次數有直接關系.

對于高速、高并行、低資源消耗的高性能線性代數復矩陣的優化設計而言，線性代數復矩陣的空間復雜度主要體現在計算次數和計算類型上，而時間復雜度則主要體現在計算的全過程中.若線性代數復矩陣的計算過程比較簡單，且具有較高的并行性，將大大降低線性代數復矩陣在時間和空間上的復雜性.

以上分析了線性代數復矩陣的求解過程，在計算過程中可以降低復雜度，同時具有較高的并行性，節省大量的資源能耗，在完成線性代數復矩陣求解的基礎上，證明了線性代數復矩陣的相似標準型存在性.

2 證明線性代數復矩陣的相似標準型存在性

2.1 線性代數復矩陣的相似標準型

人們在求解線性代數復矩陣時往往希望采用簡單的計算步驟，在線性代數復矩陣中，其目的就是將線性代數空間分解成為一個個子空間的直和，找到線性代數復矩陣的標準型.而相似標準型是對線性代數復矩陣的一種精細分解，對研究線性代數復矩陣的特性、線性代數復矩陣函數具有重要作用.在線性代數中，證明復矩陣的相似標準型存在性都是構造出來的，通常有兩種形式：

①根據線性代數復矩陣的特征多項式得到矩陣的準素分解和循環分解，再推導出線性代數復矩陣A的相似標準型；

②將λ?線性代數復矩陣的理論應用到A的特征矩陣中，得到矩陣A的標準型.

以上兩種形式的優點是只給出了線性代數復矩陣A的相似標準型的具體步驟，但無法從根本上說明線性代數復矩陣為什么會有相似標準型.本文利用模理論的相關知識，證明線性代數復矩陣存在相似標準型.

假設存在整數環Z與加群G，對任意一個元素n,m∈Z，u,v∈G，整數環Z與加群G的元素之間存在如下關系：

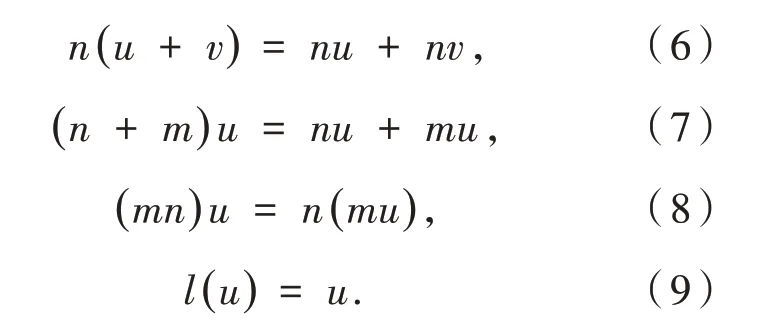
將上述關系進行一般化處理，即一個整數環作用到一個加群上，就可以得到模的概念.

定義1［10]：假設R是一個具有單位元1的整數環，M是加群，同時還存在R×M到M之間的運算°，如果針對a,b∈R，u,v∈M，R×M到M之間的運算°就會滿足下列關系：

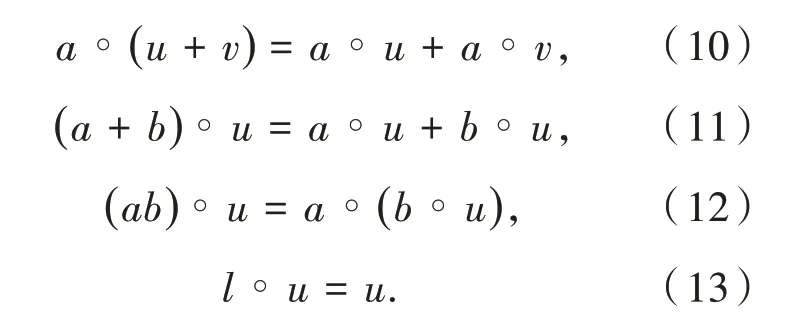
因此，稱M是整數環R上的模，通常將其記作R?模M，那么加群G很顯然就是一個Z?模.

在上述推導的基礎上，文中給出下列定義.

定義2［11]：R?模M的子集N又可以被稱為M的R?子模，如果存在R°N?N，那么就可以推導出R°N={a1u1+a2u2+…+anun|ai∈.

定義3［12]：假設N是R?模M的R?子模，針對商加群中，規定R×到的運算符號為?，運算過程為a?( )

u+N=a°u+N，a∈R，u∈M，那么就可以得到是關于?運算的R?模，并將其稱為R?模M關于R?子模的商模.

定義4［13]：假設M是R?模，Mi是M的子模，如果M滿足下列關系：

①M=M1+M2+…+Mt，m∈M，m=m1+m2+…+mt，mi∈Mi；

那么就可以將R?模M稱為子模M1+…+Mt的直和.

引理1［14]：有限交換群G可以唯一分解為素數冪循環群的和，可以假設它的階為n=是不同的素數，那么就存在：

①G=G11⊕G12⊕…⊕G1k1⊕G21⊕…⊕Gsk，其中Gij表示階為pnij

i的循環群；

在引理1的基礎上，可以輕松得到引理2.

引理2［15]：假設R?模M是加群，就會得到下列事實：

①如果元素g的階是t，( )t,s=1，那么sg的階也是t，同時還存在；

②如果g1+g2+…+gm=0，且gi的階ti兩兩互素，那么對于所有的元素i都存在gi= 0.

2.2 主要結果

線性代數矩陣的初等因子組為：λ?1，λ2+1，其無法分解為一次多項冪，無法轉化成矩陣標準型.為此，引入，其中pi是線性代數矩陣中不同的素數，所以存在：

①M=M1⊕M2⊕…⊕Mt，其 中，Mi是Z?子模，Mi中元素的階為pi的冪；

②如 果M=M1⊕M2⊕…⊕Mt=M′1⊕M′2⊕…⊕M′t，則在重新調整腳碼之后，就有Mi≡M′i.

證明，如果存在n=pm，就會使下列結論成立：

①M=Z°m1⊕Z°m2⊕…⊕Z°mk；

②如果M=Z°m1⊕Z°m2⊕…⊕Z°mk=Z°h1⊕Z°h2⊕…⊕Z°hs.

那么必定存在k=s，并且適當重新排列腳碼之后，可以得到Z°mi≡Z°hi.

然而，事實上，M存在有限生成元集，假設是M的兩個元素個數相等的生成元素集合，相應的階集合是，如 果 存 在m1+m2+…+mk＜l1+l2+…lk，就可以稱.然后選取一個元素個數最少并且在以上關系條件下是最小的生成元素集合，可以嘗試記作，其中對應的階數為，最 后 有M=Z°g1+…+Z°gk.

根據上述證明步驟可知，G是M的生成元素集合，但是，由于存在psmj gj=lj gj≠0，所以ps＜prj.又因為psg′j= 0，g′j的階≤ps，因此有g′j的階＜prj，那么G小于生成元素集合，這與的定義是相互矛盾的，因此有M=Z°m1⊕Z°m2⊕…⊕Z°mk，從而完成了①的證明.證明了線性代數復矩陣都存在相似標準型.

由于Euclid環屬于主要的理想整數環，而且具有上述證明中用到的Z的性質，因此該證明可以推廣到由主理想整數環作用于加群之后所得到的模.

3 總結與展望

3.1 總結

本文提出了基于初等因子法的線性代數復矩陣相似標準型，在分析線性代數復矩陣求解的基礎上，優化了線性代數復矩陣運算算法，在算法優化過程中，主要是由線性代數復矩陣的運算單元、控制單元、交叉匹配模塊、地址生成單元以及存儲單元等多個部分組成的，一般情況下，可用來計算16到128之間的2n階單精度線性代數復數矩陣.

通過對線性代數復矩陣的相似標準型進行性能分析和驗證，本文提出的定理可以在線性代數復矩陣求解的基礎上滿足相似標準型的處理速度快、運算性能高、計算準確率高等要求，從而證明了線性代數復矩陣存在相似標準型.本研究的創新點如下：

（1）研究了線性代數復矩陣在運算過程中的運算原理和算法，并對其進行了對比和分析，采用原位替換算法對線性代數復矩陣進行了逆運算，同時，基于線性代數復矩陣求逆過程中實部矩陣與虛部矩陣之間的相互交叉運算，對線性代數復矩陣的各個運算模式和存儲模式進行了優化設計，并且在滿足線性代數復矩陣運算性能的前提下，減少運算過程中的資源消耗.

（2）在線性代數復矩陣的相似標準型存在性證明中，本文提出了一個針對線性代數復矩陣求解的定理，在保證并行度高且高維計算的條件下，平衡了線性代數復矩陣在資源消耗、運算速度、元素安全以及存儲接口上的問題.通過將線性代數復矩陣求解算法與數據存儲方式相結合的形式，采用線性代數復矩陣求解模塊中的運算結構復用、模塊復用，充分開拓出線性代數復矩陣存在相似標準型的并行度，從而提高相似標準型的求解性能.

3.2 展望

本文在證明線性代數復矩陣存在相似標準型的過程中還存在一些不足，具有一定的改進空間，對于線性代數復矩陣存在相似標準型的研究還可以作進一步地優化，在以后的研究中，優化工作主要有以下幾點.

（1）本文在證明線性代數復矩陣存在相似標準型過程中只針對二階矩陣，今后還可以適當作進一步改進，將線性代數復矩陣是否存在相似標準型這一問題擴展為任意維度的證明中.

（2）本文在證明線性代數復矩陣存在相似標準型過程中只考慮到線性代數復矩陣是否存在相似標準型的求逆方案，在后續的研究中可以適當集成多種運算方案，例如實數矩陣與復數矩陣相乘、逆求解實數矩陣以及矩陣間的轉置運算等，從而實現線性代數復矩陣運算資源的極大化利用.

（3）針對維度較大的線性代數復矩陣，可以嘗試將本文的證明過程與分塊矩陣的求解相結合，將待求解的線性代數復矩陣進行分塊處理，對單個線性代數復矩陣塊采用寄存器堆緩存的方式來求解線性代數復矩陣，從而平衡線性代數復矩陣的存儲接口，分塊矩陣的求解方式對大維度的線性代數復矩陣求解具有非常強的可拓展性和實用性.

（4）在今后的研究中，可以將大維度的線性代數復矩陣求解作為證明的基礎，進而證明線性代數復矩陣中存在相似標準型.