關于復合函數極限運算法則及泰勒公式的一個注記

吳世玕

無論是數學分析還是高等數學，都介紹了復合函數極限運算法則及泰勒公式.復合函數極限運算法則一般陳述如下：

設函數y=f[g(x)]是由函數u=g(x)與函數y=f(u)復合而成，f[g(x)]在點x0的某去心鄰域內有定義，若，且 存 在δ0＞0，當x∈時，有g(x)≠u0，則A.［1?2]

法則中提出限制性條件：“存在δ0＞0，當x∈UO(x0,δ0)時，有g(x)≠u0”，為何要有這個限制性條件，文獻［3?5]用具體實例說明，如果沒有上述條件，法則的結論就有可能不成立，或者說，沒有這個條件，法則就更不容易證明.但這些文獻，并沒有從理論上分析，為什么要在法則中提出這個限制性條件.

文獻［2]中，提出用n次多項式pn(x)近似一般的復雜函數f(x)，類似于微分概念，要求誤差為.緊接著又提出要求，= 0,1,2,…,n.從而推導出f(x)的n階泰勒公式.初學者會有這樣的疑惑：教材上提的要求有點太多，或者說，這兩個要求是否矛盾.當然，教材上證明了它們不會產生矛盾，這兩個要求是相容的.作為教師，要站在學生的角度，從探求的角度去發現結論，而不是先給出結論，再來證明結論.可以從第一個要求出發，去發現f(x)的n階泰勒公式的系數，這樣更貼近初學者的認識規律.

1 復合函數極限運算法則中限制性條件g(x)≠u0的理解

1.1 用極限定義解釋函數極限運算法則中的限制性條件g(x)≠u0

若函數y=f(u)在u=u0點處無定義，而在討論極限時，極限定義中要求f[g(x)]在x0點的某個去心鄰域內有定義，因此，就要求在內，g(x)≠u0.

若函數y=f(u)在u=u0點處有定義，但f(u0)≠A.且要求結論

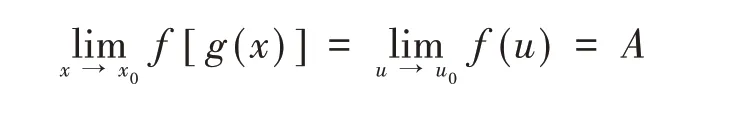
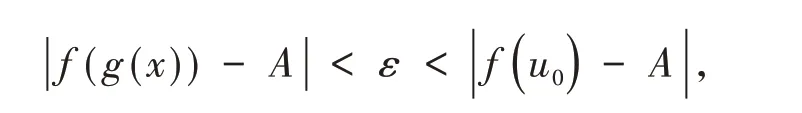
那么，何時可以去掉限制性條件“存在δ0＞0，當時，有g(x)≠u0”？由以上分析可知，若函數y=f(u)在u=u0點處有定義，且，則可以去掉這個條件.也就是說，當函數y=f(u)在點u0處連續時，可以去掉這個限制性條件.

1.2 用實例解釋復合函數極限運算法則中的限制性條件

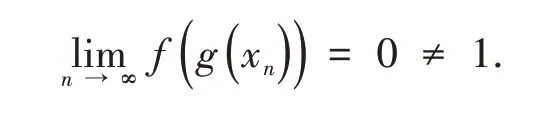
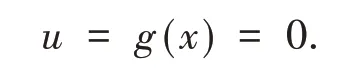
在利用無窮小等價替換求極限時，復合函數極限運算法則起到很重要的作用，比如x→0時，

利用復合函數極限運算法則，只要在x的某無限變化過程中，φ(x)→ 0,φ(x) ≠0，就有

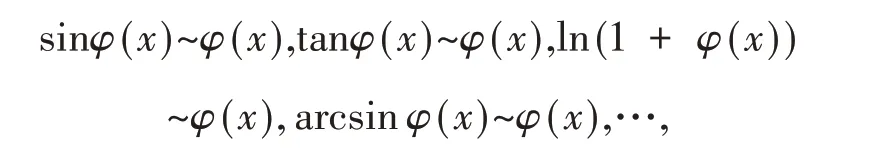
其中要求φ(x)≠0，就是復合函數極限法則中的限制性條件［6].

2 泰勒公式的系數

泰勒公式的系數是用導數計算的，但有時，高階導數比較難求，或高階導數公式很麻煩，可以通過其他方法求泰勒公式的系數.特別是求復合函數的泰勒公式的系數，可以嘗試通過極限方法求出.

2.1 用極限方法推導泰勒公式的系數

設f(x)在x0處具有n階導數，且

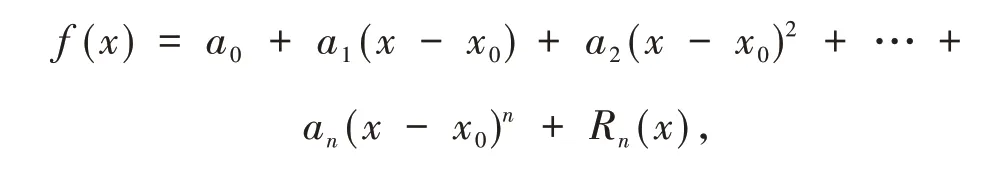
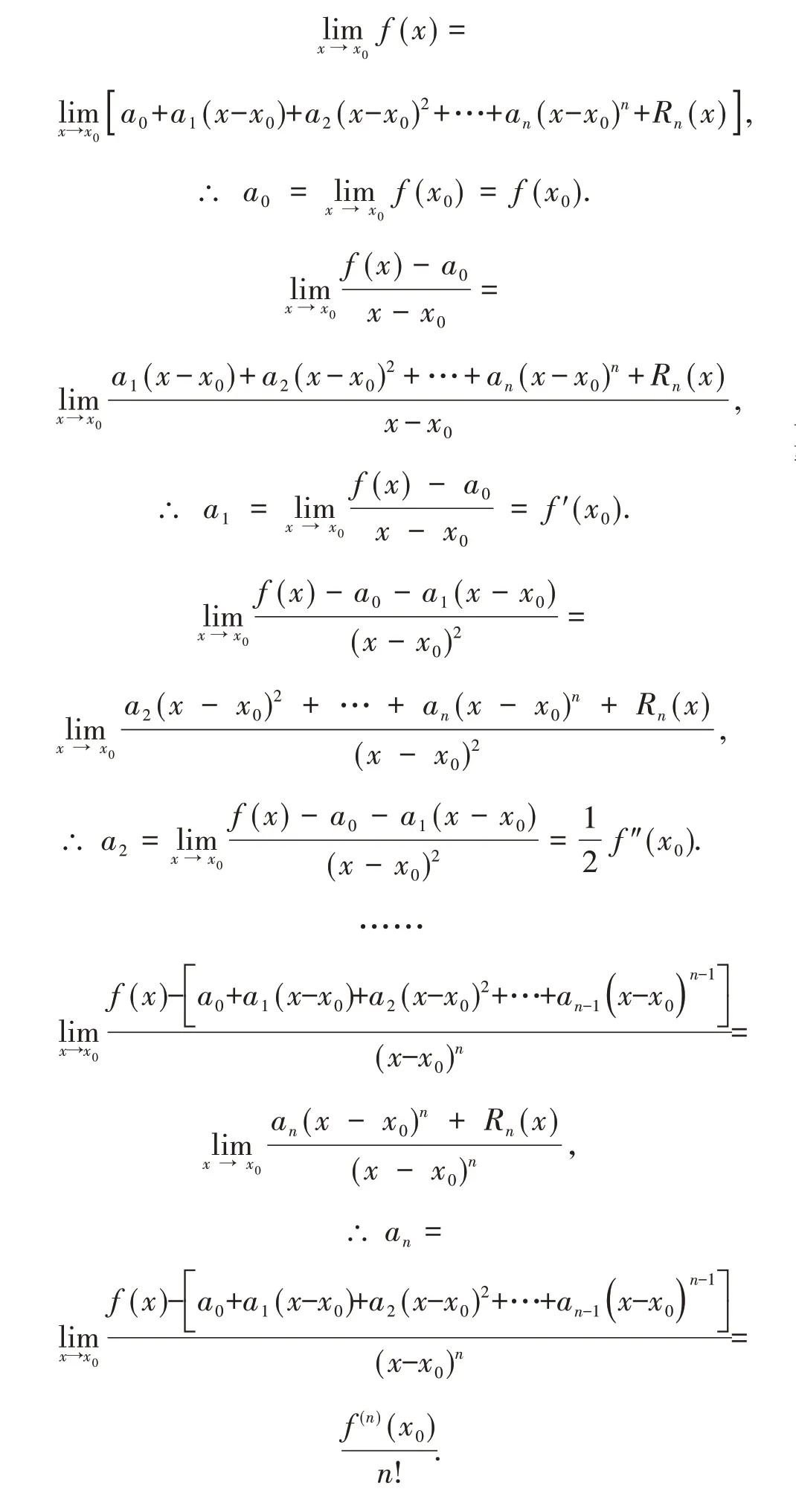
反之，記

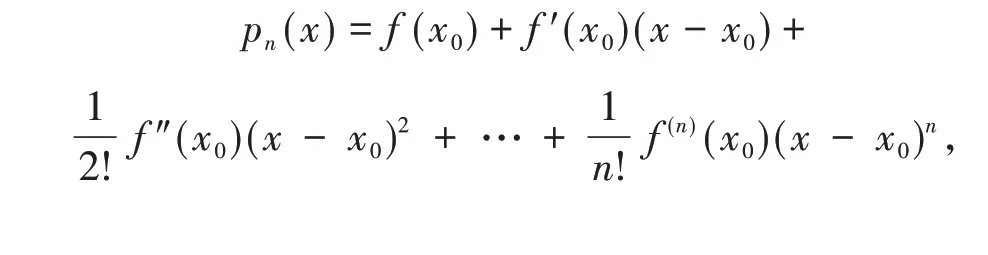
則可證明，f(x)=pn(x)+Rn(x),其中Rn(x)=且0,1,2,…,n.（文獻［2]有證明過程）.

這里提供了求泰勒公式系數的一種新方法，通過極限求泰勒公式的系數.

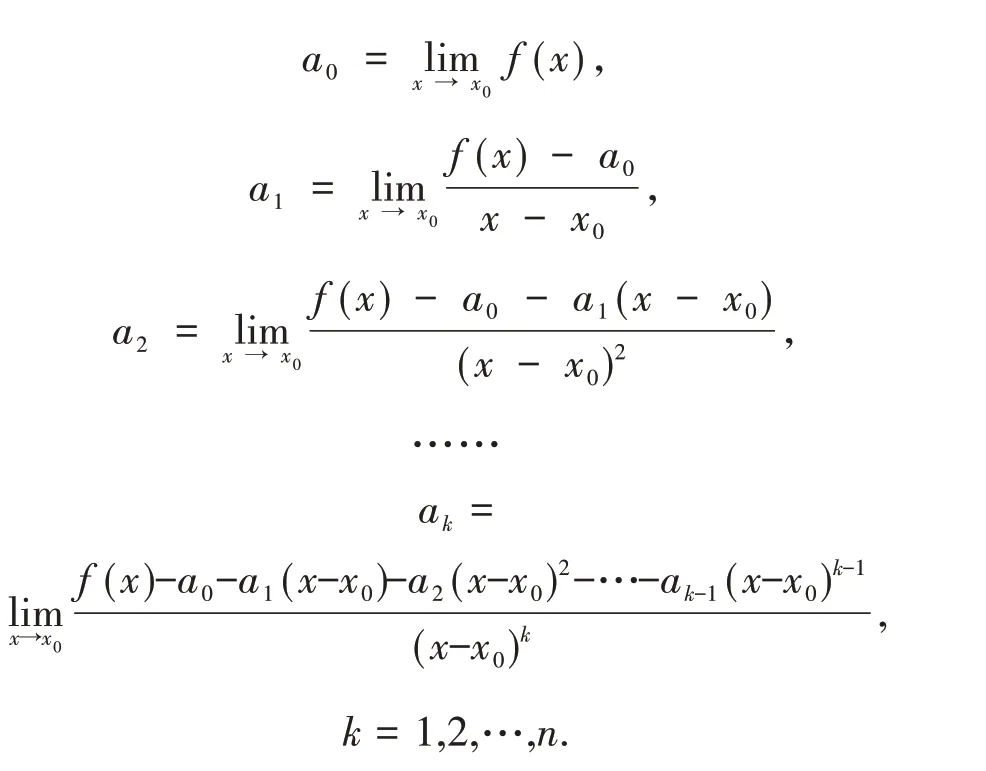
求極限過程中，除了用洛必達法則外，無窮小等價替換、極限四則運算方法、復合函數極 限 運 算 換 元 法［7?10]，都 是 常 用 方 法.求ak時，不一定要求出f(k)(x).當f(k)(x)表達式較難求出時，用極限方法，有時也能求出系數ak.

2.2 用極限方法求泰勒公式的系數舉例

例2 求e2x?x2包含x3項的帶有佩亞諾余項的Taylor公式.

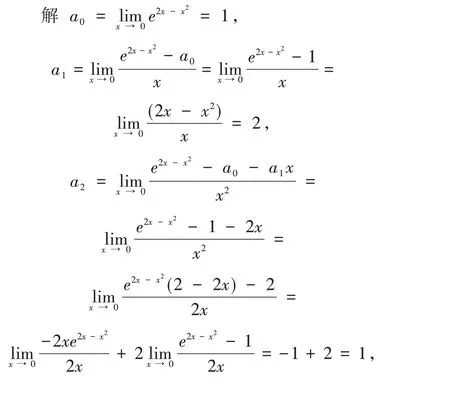
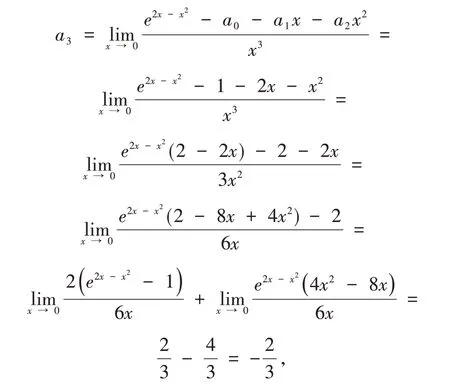
所以，e2x?x2=1+2x+x2?

3 結語

學習高等數學，不僅要知曉各概念、定理、公式的定義、使用條件、使用方法，更要知曉定理中為何會有一些限制性條件.作為高等數學教師，在講解比較難的定理時，不妨先從實例出發，引出要講解的定理結論.更重要的是，不僅要教學生如何證明定理結論，更要從理論上，讓學生多想一想，定理中為什么要有這些條件.最好是從理論及實例兩方面加以解釋，這樣，可讓學生對定理有個更加清晰的認識.教學，不能強迫學生接受教師講的結論，要從多方面講清楚知識要點.要培養學生創新意識，不要拘泥于教材上的知識，要大膽地創新探索，要有自己的想法.