一種非相干復合網格解調算法的連續相位調制

司維, 張明

(1.河南省外貿學校 信息服務辦公室， 河南 鄭州 450002;2.河南水利與環境職業學院 機電與信息工程系， 河南 鄭州 450002)

0 引言

近年來，通信系統對于頻帶資源的要求越來越高，通信系統的傳輸速率往往需要更寬的頻率帶寬或者增加發射功率[1]，對于某一頻段的帶寬增加是無法做到的，僅僅能通過增加發射功率提升傳輸速率。通信設備實現功率的增大的方法不外乎于設備體積的增大或者是高功率持續工作時間的減少。上述兩種因素都會造成通信帶來的通信效率的降低，不利于通信設備的小型化或者便攜化[2]，綜合這些因素，連續相位調制這種高效的信號調制方式被提出來。連續相位調制具備的抗失真能力可以降低信號放大器的成本。由于在頻域中主瓣處在帶內位置，頻譜泄露較小[3]，其頻譜利用率極大的提高，但由于調制參數較多，其解調算法比較復雜，是本文討論的重點。

1 連續相位調制理論

1.1 連續相位調制信號的數學模型

連續相位調制的傳輸系統中，基帶的二進制連續相位調制信號的等效低通表達式為式(1)。

(1)

其中，fc代表載波頻率;Es代表每個符號的能量;α={αi}代表取自集合{±1}的碼元序列，里面的相位函數Ψ(t,α)是以時間t為變量的連續函數，保證了相位連續性，Ψ(t,α)的具體表達如式(2)。

(2)

其中,h是調制的指數，h意味著連續調制相位是否為單調制。

基帶相位脈沖的信號為式(3)。

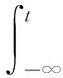
(3)

那么連續相位調制信號表達式為式(4)。

(4)

由上面連續調制信號的數學表示可以看出，該信號是包絡恒定的，由此得到的相位積分相位脈沖信號是連續的[4]，抗非線性失真的能力增強，連續相位信號特性使得信號具有記憶性，相位特性需要依賴于當前信號的之前的信號相位符號，并且受到多個調制參數的影響[5]，其信號調制原理框圖如圖1所示。

1.2 連續相位調制頻譜特性

信號主瓣的帶寬會隨著單調制指數的平均值增大而增大，對于單調制參數和多調制參數，頻帶的利用率會呈現出不同的特性[6]，如果使多調制指數低于單調制參數，就會使頻帶利用率增加。調制參數的特性如圖2所示。

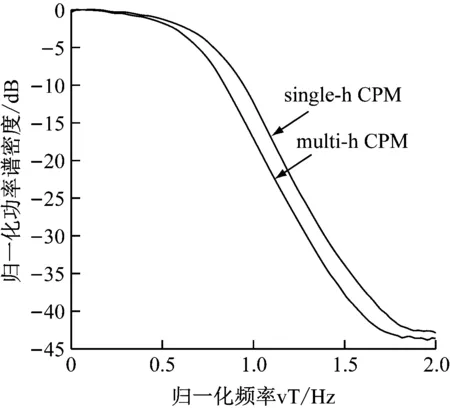
圖2 多調制參數與單調制參數的功率譜密度圖

除了調制參數會影響頻譜特性之外，也會依賴于頻率脈沖g(t)對信號功率譜密度的影響，頻率脈沖長度會很大地影響主瓣功率特性[7]，頻譜利用率越高的信號，其旁瓣衰減一般都會很快，這就會希望主瓣的帶寬較小，信號的功率譜密度曲線逐漸趨近于平滑，通過歸一化的處理后，不同脈沖長度呈現出曲線的形狀也非常的不一致，此時的調制指數設置為固定的值為0.5,如圖3所示。

圖3 脈沖長度分別為 1、2、3、4連續相位調制信號的功率譜密度

綜上所述，在實際的通信系統中，選擇適當的調制參數會造成不同的調制方式，參數的影響需要根據不同的應用場景而具體選擇，參數對于功率譜密度的影響需要折中的比較，通信系統的高效性會使得系統復雜度增加[8]，也會使得通信系統的可靠性受到一定程度的影響。

2 非相干復合網格解調算法

2.1 算法原理

連續相位調制信號的接收機包含執行Viterbi算法的檢測器。許多調制算法都具有對應的狀態網格圖，對于Viterbi算法的狀態圖一般被稱為基本網格圖[9]。而實現復合網格圖的基本思想是將該基本網格圖及其經過相位旋轉的網格圖組合起來成為基本單元[10]，各個部分的狀態轉移關系不會變化，而通過狀態耦合的轉移來實現連續相位調制信號的非相干的解調處理過程，對于復合網格處理之前，首先會匹配濾波，如圖4所示。

圖4 復合網格解調器框圖

對于連續相位調制信號來說，每個時刻都有對應的信號狀態[11]。例如，它的基本網格圖在時刻t時的狀態一般表示為式(5)。

Sb(n)[S1(n),S2(n),…,SNS(n)]

(5)

其中，Si(n)=[θl,Uk(n)],l=1,2,…,Np;k=1,2,…,Nc；i=(l-1)Nc+k。θl被稱為相位狀態，Uk(n)稱為相關狀態，那么對于解調算法的基本網格圖狀態總數應是Ns=NpNc，Np為相位狀態的個數；Nc為相關狀態的個數。

基本網格圖的狀態轉移矩陣，如下所述。

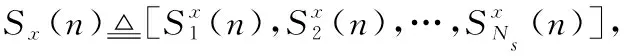
(6)

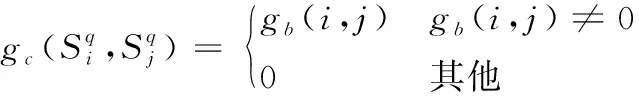
(7)

由上面的式子可以確定網格圖的基本連線方式，二進制符號(M=2)，調制指數h=0.5，脈沖記憶長度L=2時的連續相位調制信號的基本網格圖和復合網格圖,如圖5、圖6所示。

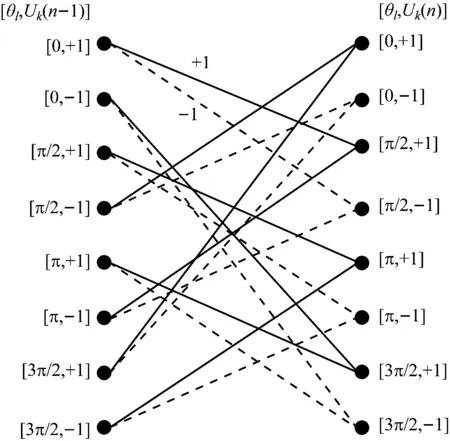
圖5 連續相位信號的基本網格圖

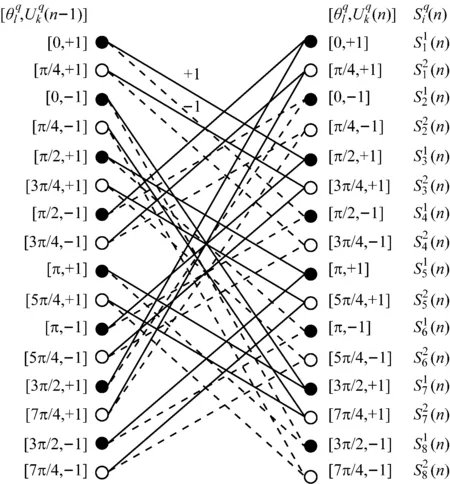
圖6 連續相位信號的復合網格圖

2.2 復合網格解調算法的模型

通過上述的分析，可以歸納出單元網格的數量既會影響到相位狀態之間的相位差，也會對算法復雜度造成一定的影響，當網格數減少時，算法的復雜度會相應地減少，從而使算法易于實現。然而只有當單元網格數量增加的時候，才會使得初相對解調的影響度下降。由于接收信號的載波頻率與系統自身的載波頻率會有相異的地方，那么對于連續相位調制信號來說，它的相位狀態就會有發生旋轉的可能性。為了消除這種頻偏對于信號解調的消極作用，可以進行狀態的耦合轉移。所謂的狀態耦合轉移就是在每隔一個周期點就在相鄰的單元網格之間引入狀態轉移矩陣，從而實現連續相位調制信號的解調算法，該算法的復雜度計算就需要考慮每個狀態的路徑計算量。

3 算法模型仿真與分析

連續相位調制信號通過該解調算法會具有抗初相的性能，再加入狀態耦合轉移后，減少初相對解調的影響，本實驗中選取M=4，h=0.25，L=2的升余弦函數的連續相位調制信號。在仿真實驗中加入高斯白噪聲信道，解碼器的反饋深度設定為20個符號深度，分析在本實驗的復合網格算法的優勢。對于周期符號點Nctd可以采取對比不同的取值進行分析，考查網格解調算法的性能，性能的表現可以通過誤比特率(BER)的方式來體現，判斷單元網格數的影響效果，將Nctd=1、Nctd=4、Nctd=8時的誤比特率結果放置于同一圖中，如圖7所示。

圖7 實驗結果對比

從該圖可以分析出當Nctd=1時，其誤比特率的結果比較大，解調效果不是很理想，當Nctd=4或者Nctd=8時，誤比特的錯誤明顯下降，說明單元網格數目的增加會改善解調的效果，減小初始相位對于解調的影響。

4 總結

本文對連續相位調制信號的非相干復合網格解調算法進行研究，詳細地分析了算法原理，針對連續相位調制信號，給出了精準的數學模型，依照分析的數學模型，研究其頻譜特性，針對連續相位信號四進制進行優化分解，研究連續相位信號的復合網格解調算法的抗初相性能。在以后的研究中，可以擴大研究的范圍，對于多進制的連續相位調制信號，可以進行探討。