基于魚眼鏡頭的樹高測量方法

宋佳音，池志祥，張曉鵬，朱慶林，宋文龍，楊柳松

(1. 東北林業大學機電工程學院，哈爾濱 150040； 2. 國網黑龍江省送變電工程有限公司，哈爾濱 150040)

森林是陸地生態系統的重要組成部分，對保持水土和維持氣候具有重要作用。及時掌握林分蓄積量及森林生物量對生態系統研究具有重要價值。樹高作為當前衡量森林系統穩定最廣泛的指標，其高度的精確測量具有重要意義[1-2]。目前常用的測量樹高方法主要有布魯萊斯測高器[3]測量和超聲波測高器[4]測量，布魯萊斯測高器結構簡單，但測量時需要先用皮尺測出儀器與待測樹木的距離，存在讀數誤差及測量精度低、應用不便等缺點；超聲波測高器是以超聲波完成距離測量，再輔助角度數據計算樹木高度，該方法測量時較為煩瑣，且超聲波測距時存在發散角，因此在林區樹木較密的情況下，信號容易被其他樹木遮擋反射，造成測距的不準確而影響高度的測量。

為提高測量精度，減小測量復雜度，近景攝影測量技術[5-6]發揮了重要作用。陳相武等[7]提出了一種基于單目視覺的立木高度測量方法，該方法具有較高的精度，但測量視角小，不能在近距離獲取樹木的完整圖像，不適用于密集的森林測量。對于解決視角問題的有效方法是采用雙目視覺測量，佘銀海等[8]提出了一種雙目視覺測量方法，該方法有效解決了測量視角的問題，但因為需要對采集的左右兩幅圖像進行特征點提取，匹配和三維像素點重建，存在特征點匹配困難的缺點。魚眼鏡頭具有短焦距、大視角的特點，且采集的魚眼圖像特征點提取簡單，宋佳音等[9]提出了一種基于半球圖像的立木高度測量方法，解決了測量視角和特征點匹配的問題，但是忽略了魚眼鏡頭虛擬距離，導致測量結果精度不足。

在魚眼鏡頭測量樹高的基礎上，現引入Scaramuzza魚眼鏡頭標定模型和魚眼鏡頭虛擬距離參數，提高測量的精確度。首先根據魚眼鏡頭成像模型確立世界坐標系與圖像像素坐標系中對應點的關系；然后以畸變系數的等距投影模型為基礎，建立測量系統模型，測量系統所需參數用Scaramuzza魚眼鏡頭標定方法求取；最后利用多算子融合算法對魚眼圖像進行輪廓提取，用改進四叉樹算法進行圖像分割，Hough變換直線檢測提取極值點，實現樹高的測量。利用手機搭配魚眼鏡頭，對黑白棋盤格進行魚眼圖像獲取，利用棋盤格內角點距離去驗證測量系統模型的準確性；對待測樹木進行魚眼圖像采集，用該測量系統模型對樹高進行反演，用提出的計算樹木高度方法與文獻[9]測量樹高方法進行對比，檢驗該測量方法的優越性。

1 魚眼相機成像模型

魚眼鏡頭成像模型能確定世界坐標系與圖像像素坐標系之間的坐標變換關系，將世界坐標系中的目標點投影到圖像像素坐標系中，魚眼鏡頭成像模型如圖1所示。

圖1中坐標系OwXwYwZw是世界坐標系，它是一個在適當空間中選取的參考坐標系，P(xw，yw，zw)表示世界坐標系中目標點P的坐標。坐標系OXYZ是魚眼鏡頭的參考坐標系。坐標系OcXcYcZc是相機坐標系，原點Oc位于攝像機光學中心，坐標軸Xc和Yc分別平行于X軸和Y軸，Zc軸是相機的主光軸實際上點Oc和O重合，P′(xc，yc，zc)是相機坐標系中點P對應的成像點，r′是點P′到光軸的距離。坐標系ouv是圖像像素坐標系，原點o是光學中心點，坐標軸u和v分別平行于Xc軸和Yc軸，P″(u，v)是圖像像素坐標系中點P對應的成像點，r″是點P″到光軸的距離。

根據等距投影定理[10]得

r′=fω

(1)

ω=tan-1(r/L)=tan-1[(xω2+yω2)1/2/L]

(2)

式中：f為光學系統的物方焦距；ω為點P相對于光軸的入射角；L為世界坐標系中的點到魚眼鏡頭中心的水平距離。

由于魚眼鏡頭存在畸變，為保證圖像的均勻性，引入失真系數λ得

r′=λfω

(3)

相機平面中心點為Oc(x0，y0)，P′點坐標為(xc，yc)，P點坐標為(xw，yw，zw)，令Xc和Yc軸方向的畸變系數分量為λx和λy，則

(4)

(5)

式中：θ為點P的方位角，也是相機坐標系中點P′的方位角。

圖像像素坐標系中心點o的坐標為(u0，v0)，P′通過等距投影得到P″，相機坐標系與圖像像素坐標系中對應點關系為

(6)

式中：mx、my為放大系數。

令kx=λxmxf，ky=λymyf，聯立式(2)～式(6)得

(7)

式中：kx、ky為畸變系數。式(7)是引入畸變系數的等距投影模型，建立世界坐標系與圖像像素坐標系中對應點的轉換關系。該模型需要求取的參數為光學中心點o(u0，v0)，畸變系數kx和ky，水平距離L。根據圖1可得

L=h+l

(8)

式(8)中：l為魚眼鏡頭的虛擬成像距離；h為世界坐標系中的點到魚眼鏡頭頂部的水平距離。

2 測量模型的建立

以畸變系數的魚眼鏡頭等距投影模型為基礎，構建測量系統模型。測量系統模型由魚眼鏡頭、測距儀和智能手機組成，如圖2所示。

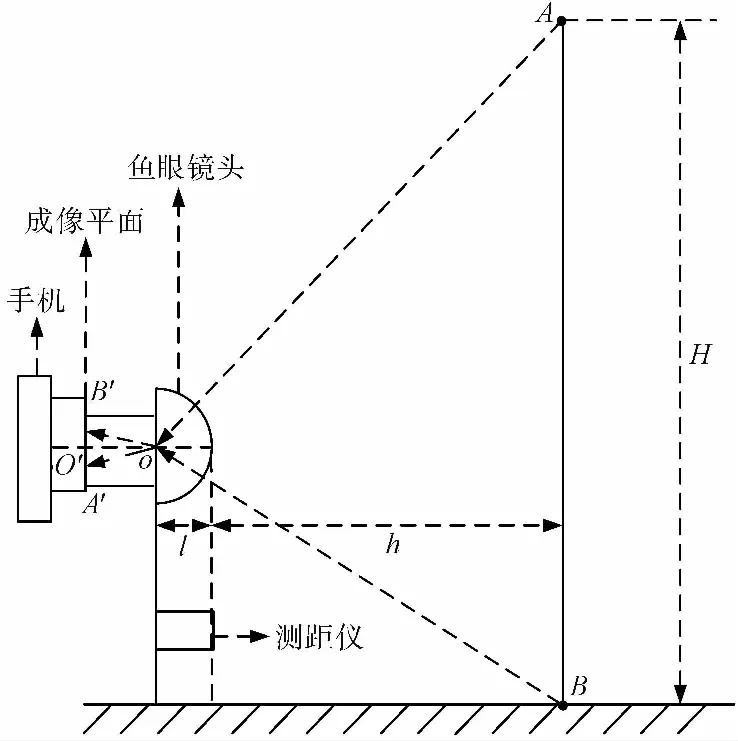
圖2 測量系統模型Fig.2 Measurement system model

2.1 測量系統數學模型

在圖2中，A′和B′為成像平面中的參考點，處于圖像像素坐標系中，設A′坐標為(uA′，vA′)，B′坐標為(uB′，vB′)。A、B為被測物中兩點，處于世界坐標系中。A′和A存在對應關系，B′和B存在對應關系，由式(7)可得，世界坐標系與圖像像素坐標系中對應點的關系為

聯立式(7)～式(9)可得

(10)

令zw=0，根據式(10)，可得坐標A(xA，yA)，B(xB，yB)的值。計算AB之間的距離H，H為測量系統模型所求的結果。

H=[(xA-xB)2+(yA-yB)2]1/2

(11)

2.2 光學中心點獲取

為獲取光學中心點，引入Scaramuzza魚眼鏡頭標定模型[11]。在Scaramuzza模型中，世界坐標系與相機坐標系中對應點的關系為

(12)

式(12)中：R為旋轉矩陣；T為平移矩陣。

相機坐標系中的點與理想圖像像素點的關系為

(13)

式(13)中： (u″，v″)為沒有發生畸變的理想圖像像素點；μ為標量因子；a0、a2、a3、a4為Scaramuzza模型的多項式系數；p為關于u″、v″的函數。

(14)

實際圖像像素坐標系中的點與理想圖像像素點的關系為

(15)

式(15)中： (u0，v0)為光學中心點； (u，v)為發生畸變的實際圖像像素坐標系中的點。

2.3 虛擬成像距離的獲取

世界坐標系是一個參考坐標系，可以人為選擇。根據式(12)，當zw=0時，zc=t3，由圖1得，世界坐標系到相機坐標系的距離為

t3=L

(16)

聯立式(8)、式(16)得

l=t3-h

(17)

2.4 畸變系數的獲取

引入畸變系數kx和ky，為求取畸變系數，確定標定板平面與成像平面的對應關系，建立標定畸變系數模型，標定板平面位于世界坐標系中，成像平面位于圖像像素坐標系中，標定畸變系數模型如圖3 所示。

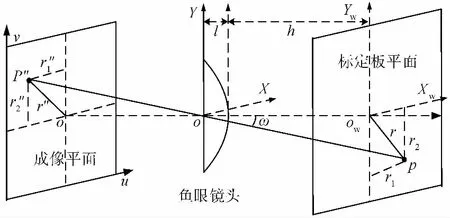
圖3 標定畸變系數模型Fig.3 Calibration distortion coefficient model

o為光學中心點，坐標為(u0，v0)，r″為點P″到光學中心點o的距離，r1″為r″在u軸方向的分量，r2″為r″在v軸方向的分量。ow為光軸與標定板平面的交點，坐標為(xow，yow)，r為點P到ow的距離，r1為r在Xw軸方向的分量，r2為r在Yw軸上的分量。

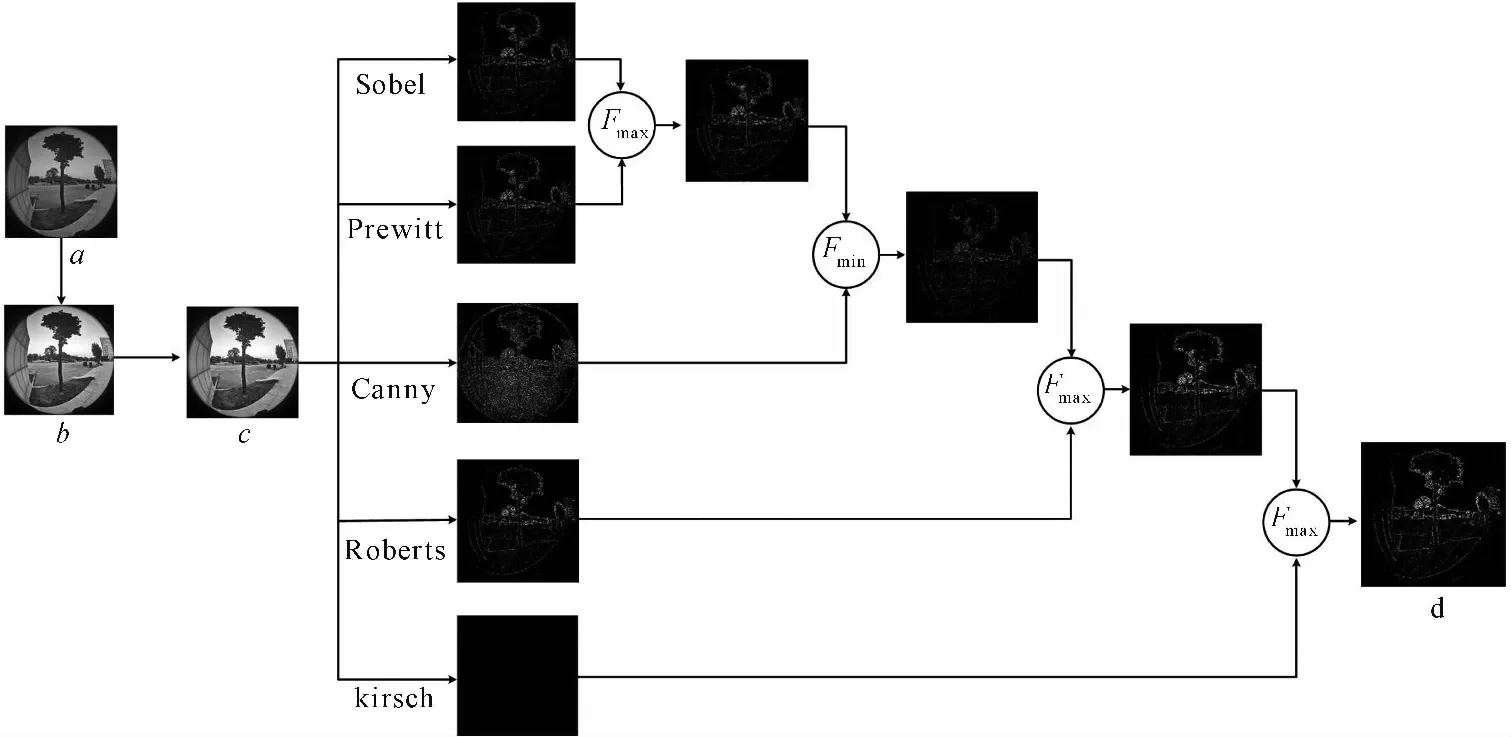
a、b、c、d分別對應圖 5中的圖5(a)、圖 5(b)、圖 5(c)和圖 5(d)； Fmax表示對兩幅圖像取合集； Fmin表示對兩幅圖像取交集圖4 多算子融合算法示意圖 Fig.4 Schematic diagram of multi operator fusion algorithm

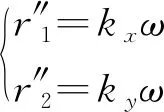
(18)

ω=tan-1(r/h+l)

(19)

聯立式(12)、式(13)、式(15)得

(20)

通過式(20)求得ow，根據圖3可得

(21)

(22)

聯立式(18)～式(22)，畸變系數的計算公式為

(23)

3 圖像處理與特征點提取

使用多算子融合算法對樹木進行輪廓提取[12]，算法步驟如圖4所示。為增強圖像的處理能力，將采集到的彩色圖像轉換成灰度圖像，如圖5(a)所示；對灰度圖像進行灰度變換增強，如圖5(b)所示；由于相機自身缺陷和外界因素的限制，使獲取到的圖像含有噪聲，對圖像進行自適應濾波去除噪聲[13]，如圖5(c)所示；多算子融合算法的輪廓提取效果如圖5(d)所示；用改進四叉樹算法對圖像進行分割[14]，如圖5(e)所示；最后運用Hough變換直線提取樹木極值點[15]，通過Hough變換檢測提取全幅圖像直線信息，標識的直線中包含著樹木輪廓的邊緣，直線的交點可以選擇性地獲取樹木輪廓極值點信息，進而得到其像素坐標值，如圖5(f)為Hough變換檢測提取的樹木圖像，選出直線相交的紅色點A即為樹木冠層的最高點，紅色交點B為樹木的最低點。

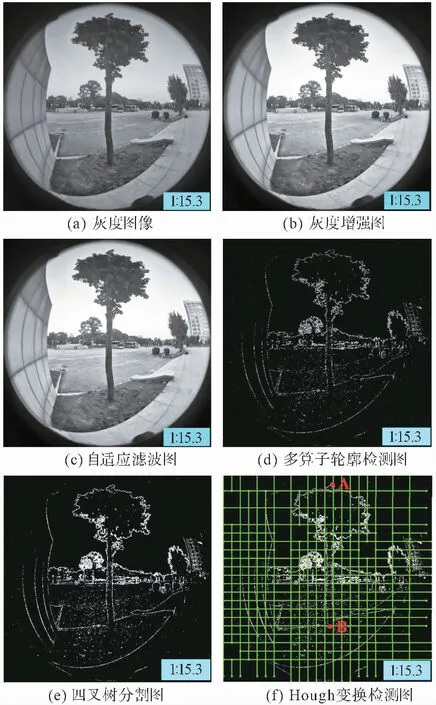
圖5 圖像處理過程Fig.5 Processing of the images

4 實驗

4.1 實驗準備

實驗設備包括手機、魚眼鏡頭、黑白棋盤標定板和激光測距儀，魚眼圖像的有效像素為3156×3156，棋盤格的間隔為50mm。選取10幅平行于標定板但距離不同的魚眼圖像。實驗在Windows10系統平臺上進行，處理軟件為MATLAB2018b。

圖 6 魚眼圖像Fig.6 Fisheye image

4.2 實驗結果分析

求光學中心點用Scaramuzza模型，直接調用MATLAB2018b自帶魚眼鏡頭標定工具箱對魚眼圖進行處理。圖6(a)是棋盤格圖，圖6(b)是棋盤格角點提取圖。求得光學中心點o(1578.50，1579.60)。

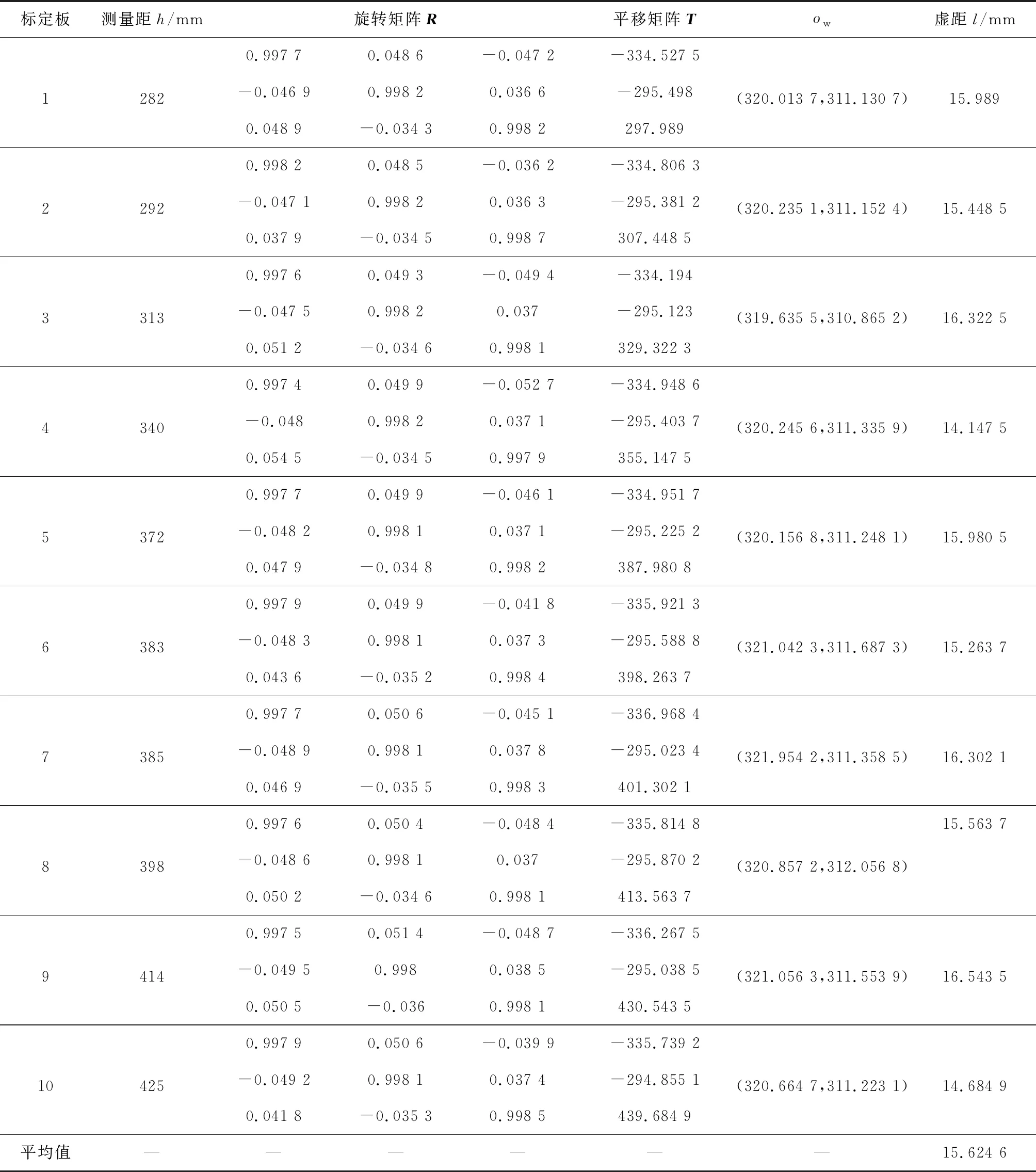
表 1 l和ow的值

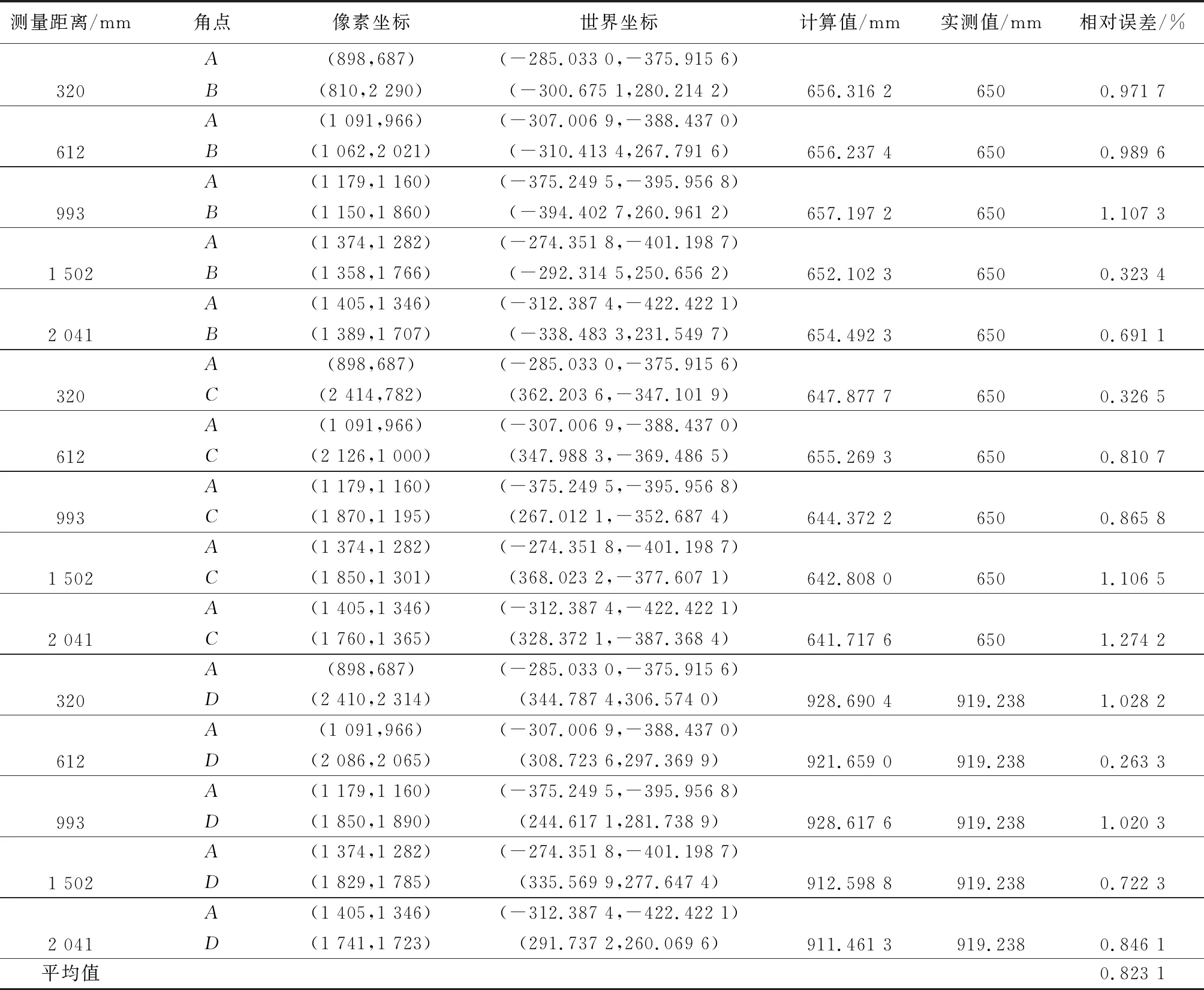
表 2 AB、AC、AD測量結果

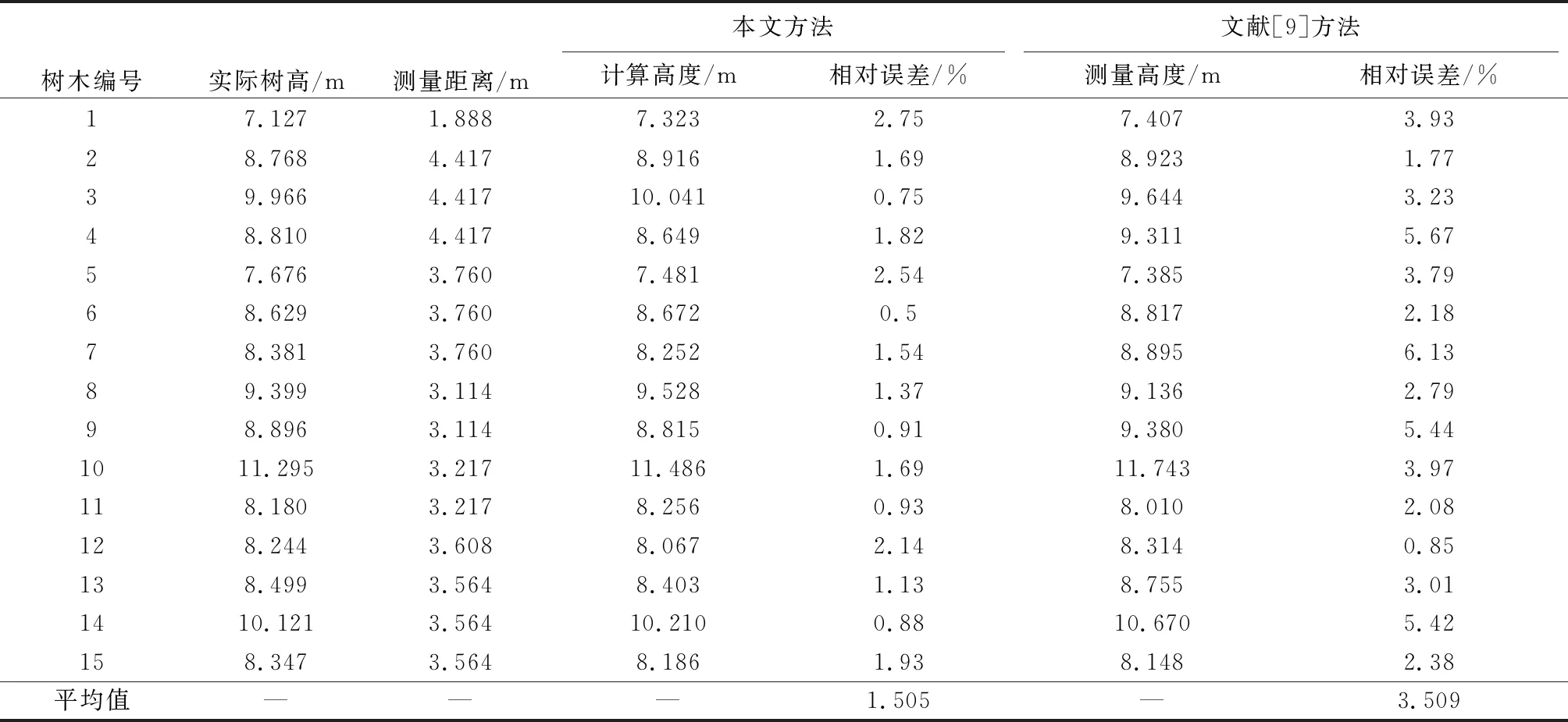
表 3 樹木高度測量結果

圖 7 kx與ky標定結果Fig.7 kx and ky calibration results

圖 8 A、B、C、D位置圖Fig.8 Location map of A，B，C and D

為驗證模型的精度，拍攝5組不同距離的棋盤格圖片，圖8為拍攝距離612mm和1502mm下的棋盤格圖。在棋盤格上取3組距離來檢驗測量模型精度。表2為AB、AC和AD之間距離的測量結果。根據表2中棋盤格的計算值與實測值的誤差分析可知，測量距離時，最大測量誤差為8.283mm，最大相對誤差為1.274%，最小相對誤差為0.323%，平均相對誤差為0.823%，證明了模型的有效性和準確性。利用模型對樹高進行測量，實際樹高用全站儀獲取，測量結果如表3所示。

表 3 可得利用本文方法測量樹高，測量誤差在-0.196～0.195m，測量最高相對誤差為2.75%，平均相對誤差為1.505%；用文獻[9]測樹高方法測量，最高相對誤差為6.13%，平均相對誤差為3.509%。通過對比可以得出所提出的測量樹高方法更加準確。

5 結論

提出一種基于魚眼鏡頭的樹高測量方法。通過建立測量模型、求解參數來反演樹高，用黑白棋盤格間的角點驗證測量模型，并通過該模型對樹木進行實驗測量，得到如下結論。

(1)棋盤格內角點間距測量實驗結果表明，棋盤格的實際距離與測量距離最大誤差為8.283mm，最大相對誤差為1.274%，最小相對誤差為0.323%，平均相對誤差為0.823%，說明了該測量模型的有效性。

(2)用該測量模型對樹木高度進行測量，測量誤差介于-0.196～0.195m，樹木測量最高相對誤差為2.75%，平均相對誤差為1.505%，與文獻[9]提出的測量方法進行對比，測量誤差更小，測量結果更加精確。