基于自適應成長法的舵面結構動力學拓撲優化設計方法研究

鄭昌隆，丁曉紅，沈 洪，趙利娟

（1.上海交通大學機械與動力工程學院，上海 200240；2.上海理工大學機械工程學院，上海 200093；3.上海云天聯合發展有限公司，上海 201109）

0 引言

未來飛行器設計追求更短的設計周期，而舵面作為彈體的重要部件，是飛行器主要承力部件之一，需要具有良好的氣動性能，并滿足重量輕、承載大等結構設計要求，以保證在各種使用環境下正常工作［1］。目前，在工程上常采用調整配重和改變舵軸等方法來提高舵面力學性能，針對不同型號，需要不斷校驗結構并更新設計方案，耗費大量時間精力，且可能引起飛行器總體指標性能的下降［2-4］。

結構拓撲優化是用于結構概念設計階段的一種優化設計技術，能在給定的設計空間、支撐條件、承載條件和工藝設計要求下，確定結構材料的最優分布形式，同時使結構的某些性能達到最優［5］。近年來，相關研究人員將拓撲優化技術引入到了舵面骨架設計中［6-7］，顯著提升了舵面結構性能及設計效率。但基于變密度法優化所得的舵面骨架構型較為復雜，制造難度很大，限制了其在舵面結構設計中的應用。而作為一種新興仿生拓撲優化設計方法，自適應成長法使用梁單元、殼單元來模擬加強筋，并在優化過程中不斷“生長”“分歧”“退化”，逐漸獲得最優的加強筋拓撲結構。相較于以單元密度為設計變量的變密度法，自適應成長法具有優化效率高、優化結果清晰、可制造性強等優點，近年來被廣泛運用于板殼結構加筋靜動態優化設計［8-13］及三維箱體結構加筋靜力學優化設計中［14-15］。

本文將自適應成長法引入舵面骨架構型設計中，通過尋找骨架的最優結構形式來提高舵面結構的動力學性能，并實現結構輕量化設計；然后與原始舵面結構性能進行對比分析，從而驗證自適應成長法對舵面骨架構型的優化效果。

1 自適應成長法

生物結構經過自然選擇與進化實現優勝劣汰，最終形成最優的結構形態。仿生學由來已久，生物學、動力學等學科的發展促進了仿生設計學的發展。19世紀，世界上第一架滑翔機基于鳥的飛行形態問世；基于蝙蝠回音原理發明了雷達；根據青蛙眼睛的特殊構造研制了電子蛙眼，用于監視飛機的起落和跟蹤人造衛星；根據空氣動力學原理，仿照鴨子頭部形狀設計了高速列車；模擬蒼蠅楫翅的天然導航作用制成了震動陀螺儀，使得飛機火箭等設備能夠實現自動駕駛。仿生學雖然取得了眾多不菲的成就，但目前仍然處于發展初期，因為大多結構仿生設計只是單純地進行結構模擬，對其內在影響因素的研究還不夠深入。

仿生優化是通過模擬自然界生物進化或者社會行為而提出的一種設計優化方法，隨著計算機技術的普及而得到發展。該設計方法由于實現簡單、設計靈活性好、效率高而被應用于工程領域。丁曉紅等［8-9］通過研究自然界分枝系統的形成機理，提出了一種基于植物根系形態自適應成長規律的板殼結構加強筋設計方法，即自適應成長法。

1.1 自適應成長法基本原理

自然界分枝系統具有清晰的分布形態，這些分枝系統都可以根據外部環境的刺激和內部營養要求等來改變本身的發育及其生長的方向，調節自身結構，以滿足內部需求并適應外部環境，最終實現一個最優的過程。圖1是幾種常見的自然界分枝結構。觀察分枝形態，可以發現它們分枝的共同特點：植物根系總是從種子點出發，樹木總是從樹根部出發，珊瑚總是從根部出發，葉脈總是從葉柄點出發。它們都為適應其生長環境自動生長、分歧、穩定，且始終朝著最有利的方向成長，如盡可能多地吸收養分和水分，盡可能多地吸收陽光，最有效地承受諸如生物本身重力、風雨雪載荷等地面上載荷，使整個結構的力學性能最優。

圖1 自然界分枝系統Fig.1 Biological branching systems in nature

加筋板殼結構受到一定的外載荷作用，可類比于自然界分枝網的生長環境，通過研究分枝系統的形態形成機理，建立一種基于這種形成機理的結構加筋板分布優化設計方法，就能實現類似于生物分枝系統的具有最優性能的加筋板分布設計。如植物根系的成長過程，主根總是從種子出發，依據自適應成長規律，沿著能使其整體功能最優的方向成長并分歧毛根。自適應成長過程如圖2所示。

在加強筋分布設計中，首先根據承載和約束條件，確定若干“種子”位置，如圖2（a）中的圓點，與“種子”相連的加強筋可以根據一定的規則成長或退化；加強筋長到一定的尺度，則可以“分歧”，與“分歧點”相連的加強筋在下一步迭代中可以參與成長或退化；加強筋退化到一定的尺度，則“消失”，過程如圖2（b）～（c）所示。這個過程反復進行，直至滿足收斂條件，結束成長。

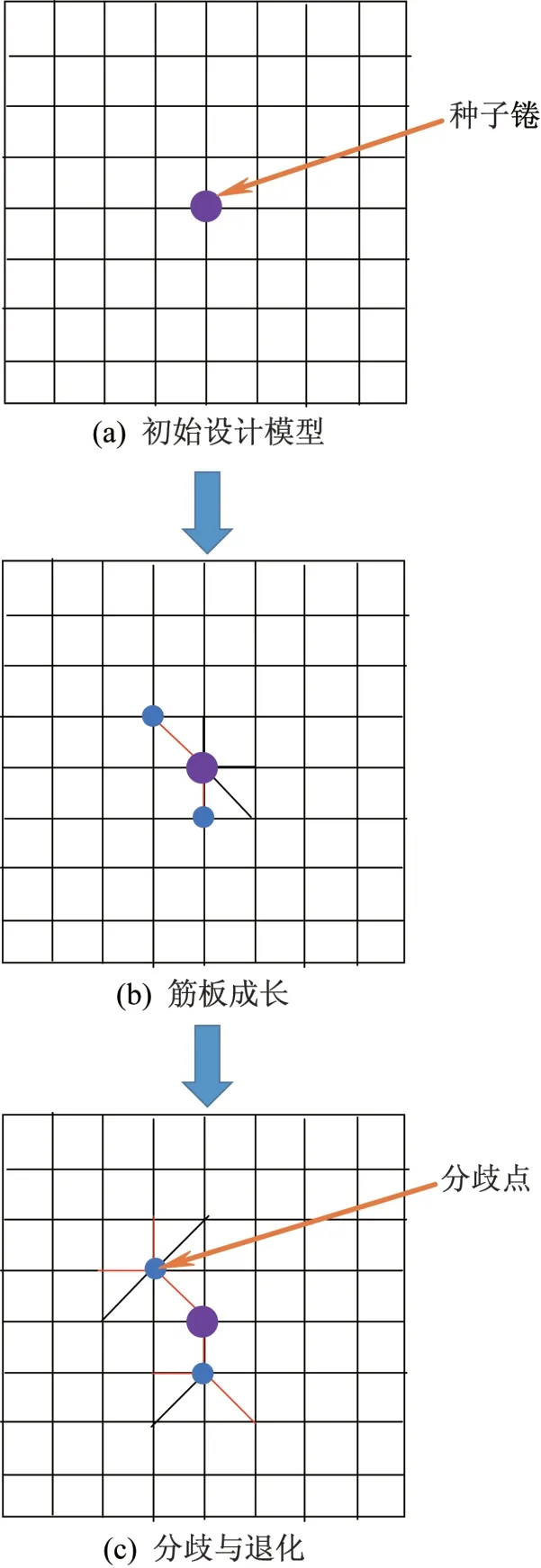
圖2 自適應成長過程Fig.2 Growth process of adaptive growth

1.2 自適應成長法仿生優化數學模型及求解

板殼結構加筋板分布優化設計問題可以表述為：以筋板的厚度作為設計變量，在一定的體積約束下，尋求結構在某種載荷工況下的某種力學性能最優。因此板殼結構加筋板分布優化設計的數學模型可表示為

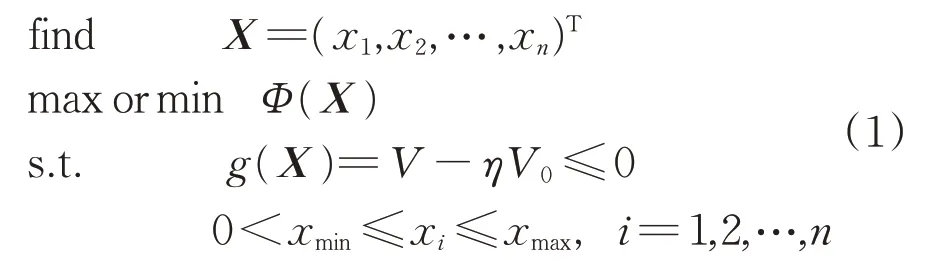
式中：X為設計變量；xi為第i個活動筋板單元的截面積；n為加強筋單元的總數；Φ（X）為目標函數；V和V0分別為整體板殼結構的總體積和初始體積；η為體積約束因子；xmin和xmax分別為設計變量xi的取值下限和上限；g(X)為約束函數。

自適應成長法的尋優迭代公式可基于最優準則法推導。基于KKT（Karush-Kuhn-Tucker）條件最優準則法推導筋板成長公式，建立拉格朗日方程為

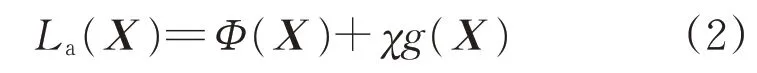
式中：χ為拉格朗日乘子。

在最優X*處，式（2）應滿足KKT必要條件，即

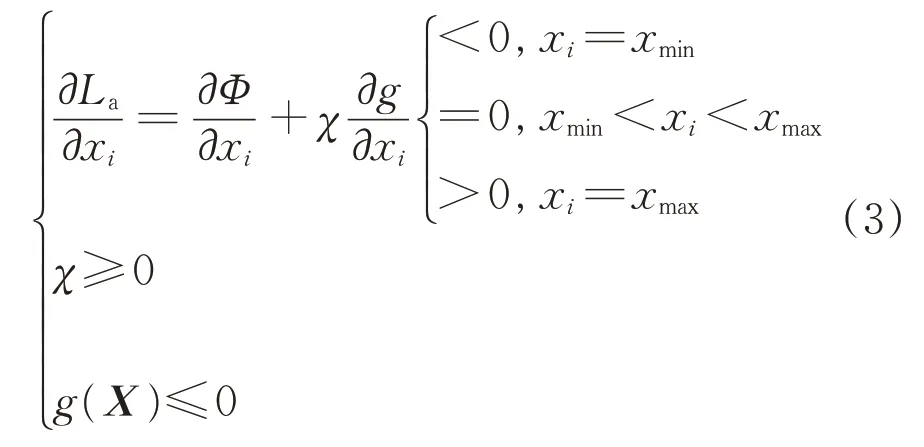
當xmin＜xi＜xmax時，根據式（3）可得

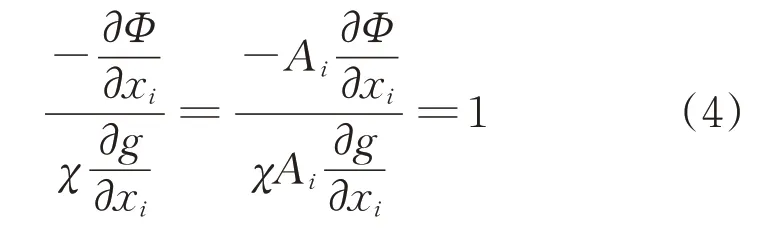
式中：Ai為第i個筋板單元的截面積。

總目標對設計變量的靈敏度為

整體結構的總體積V可表達為

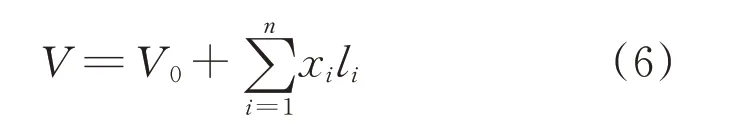
式中：li是第i個筋板單元的長度，即

將式（5）和式（7）代入式（4）可得

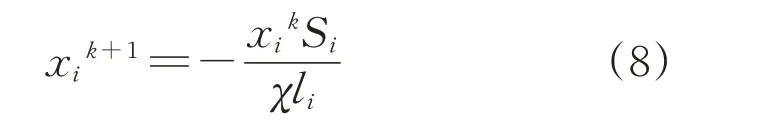
式中：k為迭代步數。為了保證收斂性，引入步長因子α，從而設計變量Ai的迭代公式為

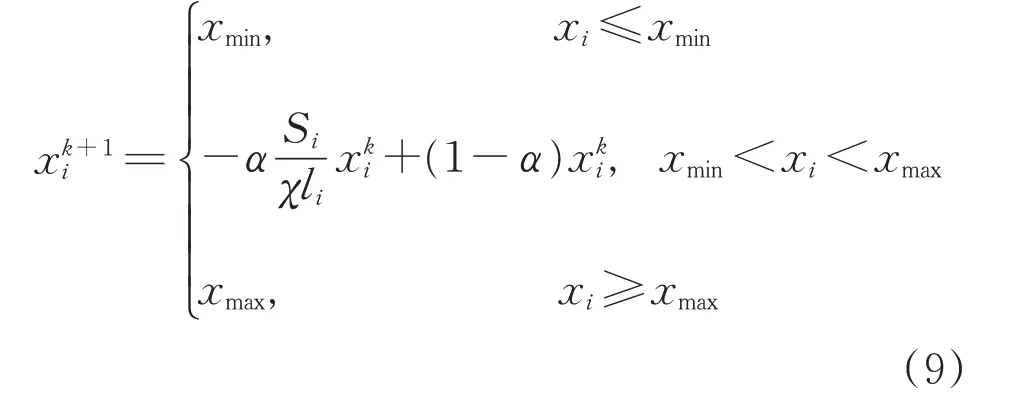
拉格朗日乘子為

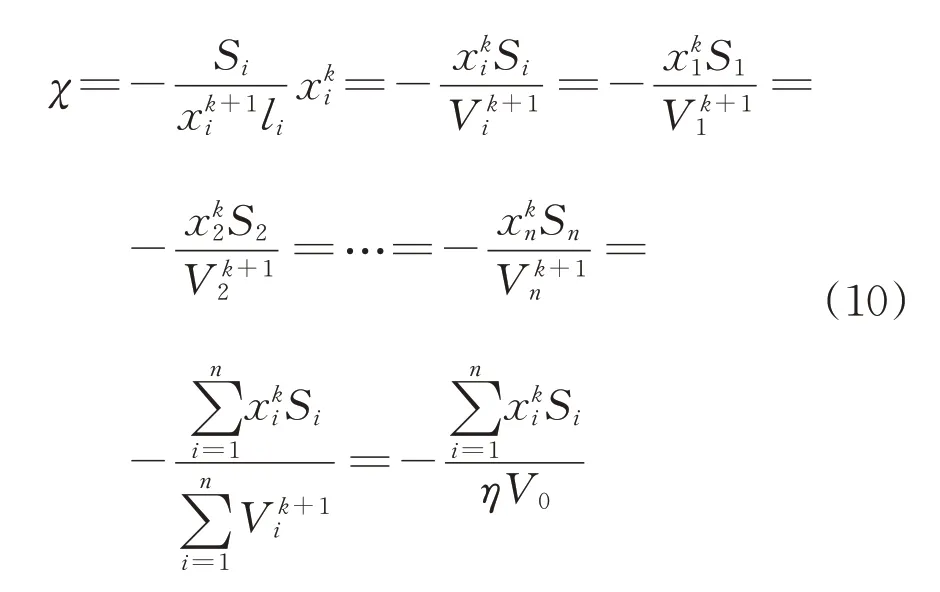
1.3 自適應成長法優化設計流程

基于自適應成長技術的基本原理，以式（9）為尋優迭代公式對結構進行加筋板分布優化設計。具體流程如圖3所示，主要包括以下4步。

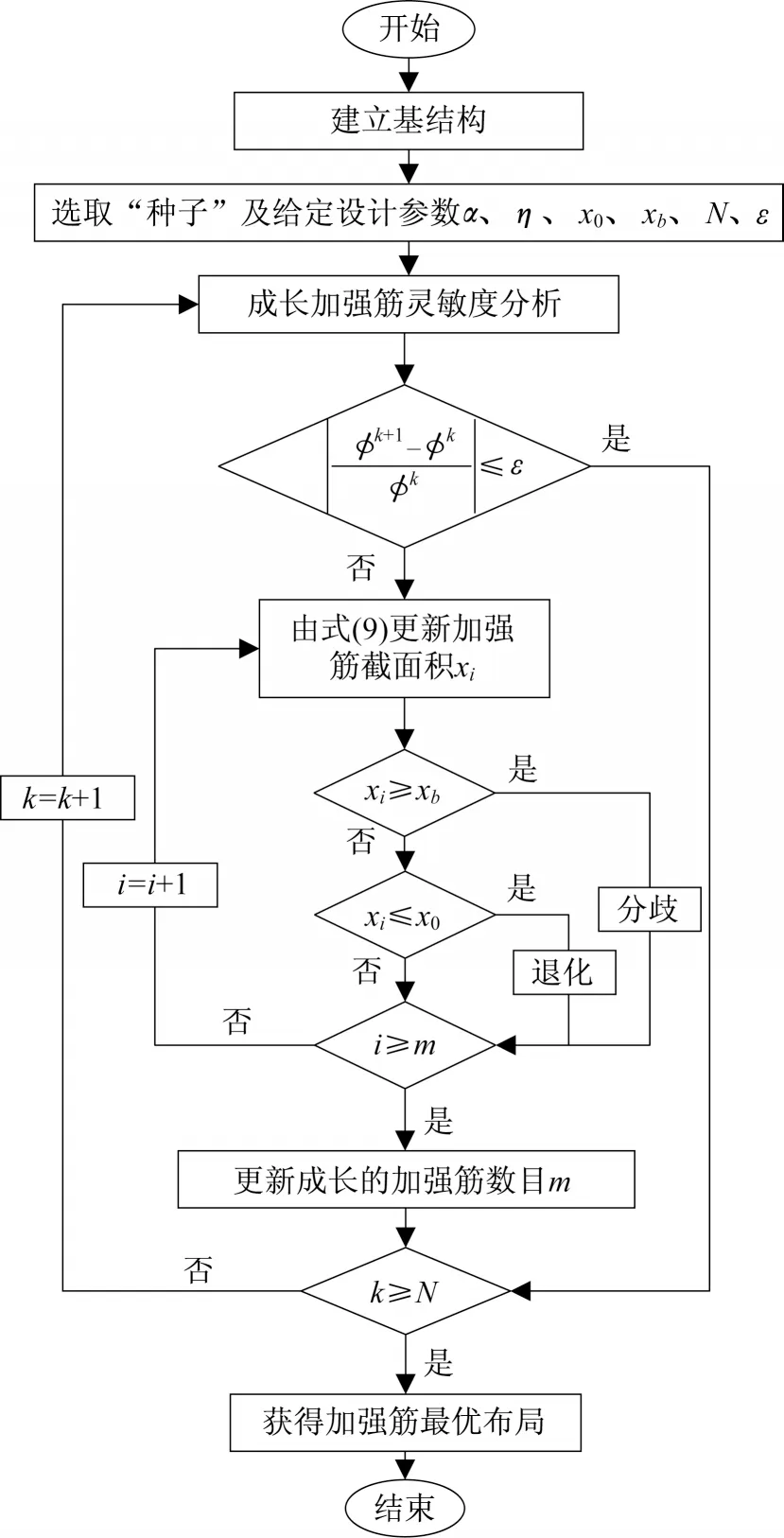
圖3 自適應成長法優化設計流程Fig.3 Flow chart of optimization design of adaptive growth method

1）建立基結構，設置設計域與非設計域。將設計對象進行簡化，并對結構離散，建立基結構，根據設計要求設置非設計域和設計域。

2）選取“種子點”，設置優化參數。根據結構的支撐和承載情況，選擇基結構上若干點為“種子點”。給定步長因子α、加強筋的初始厚度x0及分歧臨界值xb、加強筋的總體積約束因子η、收斂容差ε以及最大迭代次數N。

3）靈敏度分析。對結構進行有限元分析，計算活動筋板單元的靈敏度。

4）成長和重建。判斷活動筋板單元的狀態，如果滿足成長條件，通過式（9）更新xi；如果筋板厚度滿足xb，則該筋板單元分歧；如果滿足退化條件，則該筋板單元退化。

如果優化迭代的目標函數連續兩次的差值小于收斂容差，或者迭代次數達到設定的最大值N，則退出循環，否則返回第4 步，繼續成長，直到達到收斂條件。

2 舵面結構仿生拓撲優化設計

2.1 優化模型構建

在優化設計前，根據舵面結構的幾何特性，創建舵面仿生拓撲優化模型。由于蒙皮舵面的邊緣最小厚度僅為1.5 mm，因此選用舵面的部分區域為設計域，如圖4所示。定義初始骨架厚度為1 mm，生成初始基結構，最終生成的骨架結構如圖5所示。

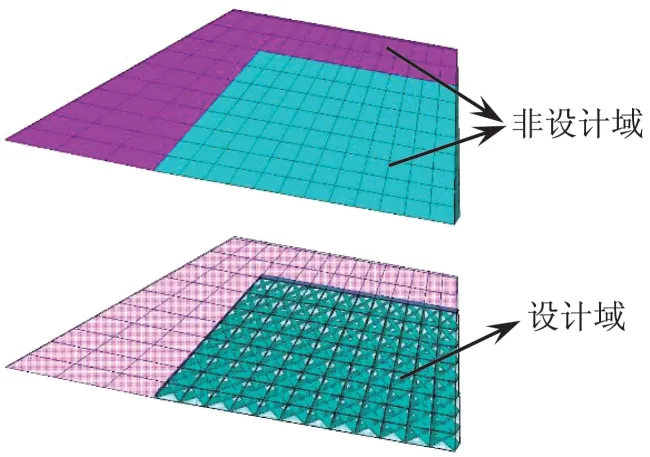
圖4 舵面骨架結構設計域/非設計域示意圖Fig.4 Design/non-design domain of the rudder skeleton structure

圖5 舵面骨架初始基結構Fig.5 Initial ground structure of the rudder skeleton

2.2 仿生拓撲優化設計

自適應成長法是基于自然界植物分枝機理而提出的，因此舵面骨架在優化初始需要指定骨架生長的初始點——“種子”。由于舵面的約束施加于舵軸上，本文優化中選用約束處作為“種子”，并在一定的設計目標和設計約束下，尋找最優的骨架結構分布形態。本文以結構的一階固有頻率最大為目標，結構體積為約束條件（總體積的30%）對板結構進行拓撲優化，優化數學模型為

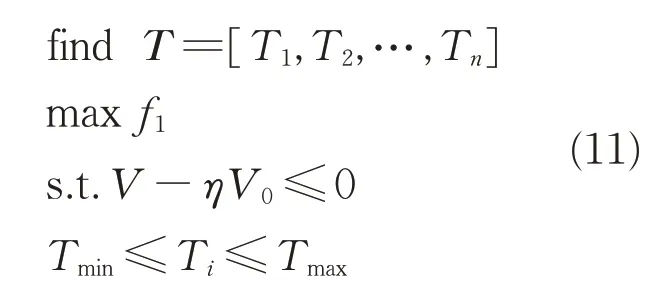
式中：T為設計變量，具體為每個骨架筋板的厚度；f1為目標函數（結構的一階固有頻率）。

經過仿生拓撲優化設計得到舵面內部骨架分布如圖6所示，優化后舵面骨架分布清晰合理，且便于進行制造。優化求解迭代曲線如圖7所示，其中為初始舵面結構的固有頻率。

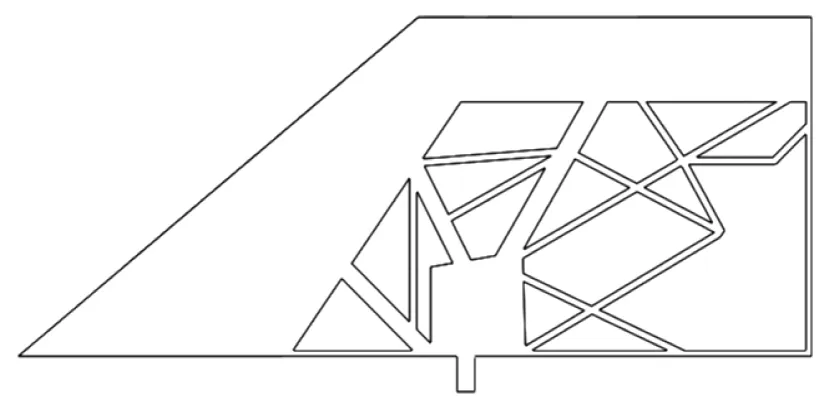
圖6 仿生拓撲優化后舵面骨架結構Fig.6 Rudder skeleton structure obtained by bionic topology optimization

圖7 仿生拓撲優化設計迭代歷史曲線Fig.7 Iteration history curve of bionic topology optimization

優化迭代過程中，舵面結構的一階固有頻率在前10 個迭代步中增長較快，之后迭代曲線逐漸趨于平緩并收斂，優化效果理想，驗證了自適應成長法的有效性及骨架優化的正確性。

3 對比與分析

為評估仿生拓撲優化效果，在HyperMesh 軟件中建立優化前后舵面的有限元模型，并在Optistruct軟件中進行有限元分析。計算得到的優化前后舵面的前兩階與顫振相關的固有振型，如圖8所示。

圖8 舵面模態振型Fig.8 Modal shape of the rudder structure

將原始舵面模型與優化后舵面模型前5階的固有頻率數值及結構質量進行對比，如表1所示。

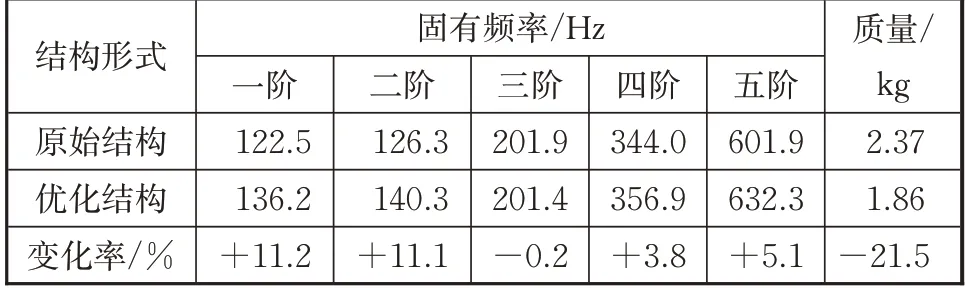
表1 優化前后舵面結構參數Tab.1 Structural parameters of the initial rudder structure and its optimized result

由表1可知優化后舵面結構的第一階固有頻率為136.2 Hz，較原始舵面結構的基頻122.5 Hz 提高了11.2%，從振型圖可知優化前后結構的振型相同。從質量來看，優化后結構的質量為1.86 kg，而原始結構的質量為2.37 kg，優化后舵結構的質量相較于原始結構質量減少了21.5%。

4 結束語

針對舵面固有頻率優化問題，利用自適應成長法，在給定設計域內對舵面內部骨架結構進行仿生拓撲優化設計，獲得了內部骨架構型，并基于有限元法對比了優化前后舵面結構的性能，驗證了舵面骨架結構仿生拓撲優化設計的有效性。自適應成長法仿生拓撲優化設計具有如下優點：

1）基于自適應成長法的舵面結構動力學設計方法能夠有效獲得滿足設計要求的清晰的筋板布局形態，并可在此基礎上獲得清晰簡潔的舵面骨架構型，從而提高結構的可制造性。同時，基于仿真的設計方法還可以有效縮短設計周期。

2）基于自適應成長法的設計方法在有效提升舵面結構固有頻率的同時，還可顯著降低舵面結構質量，實現高剛輕質結構的設計，滿足航空航天結構高剛輕質的設計需求，具有良好的工程應用價值。