基于RBF系統辨識與PID控制的收卷機張力控制系統研究

劉冠華，肖 威，韓林潔

（1.北京機械工業自動化研究所，北京 100120；2.北京機械工業自動化研究所有限公司，北京 100120）

0 引言

就收卷機張力控制系統而言，其模型的多耦合和不確定性與現場工作環境的擾動都降低了收卷機的張力控制精度。基于此，本文提出了一種使用基于徑向基函數（RBF）系統辨識與PID控制算法相結合的智能控制器，即利用神經網絡對任意非線性模型的逼近能力，將其辨識模型用于PID參數的整定，以此來提升其常規張力控制系統的自適應性，并在一定范圍內使其具有自學習能力，而后通過實驗來驗證該控制策略的魯棒性和優越性。

1 增量式PID控制策略

傳統PID控制系統結構如圖1所示。其中r（t）為系統期望輸出值，y（t）為系統實際輸出值，e（t）為偏差值作為PID控制系統的輸入量即e（t）=r（t）-y（t）。u（t）是PID控制系統的輸出量。

圖1 傳統PID控制系統結構圖

常規PID控制系統實質是將輸入量分別進行比例（P）、積分（I）、微分（D）運算并將運算結果進行線性組合求得出輸出量u（t）。u（t）的表達式如式(1)所示。

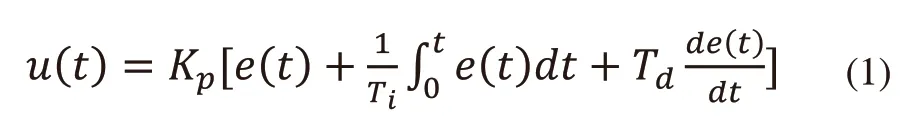
式中控制系統的輸入為e（t），控制系統的比例系數為Kp。控制系統的積分時間常數為Ti，控制系統的微分時間常數為Td。

設系統采樣周期為T，用k個采樣時刻點的總時間kT代表連續時間，將積分以累加形式表示，微分以增量形式代替，對式(1)進行離散化即：

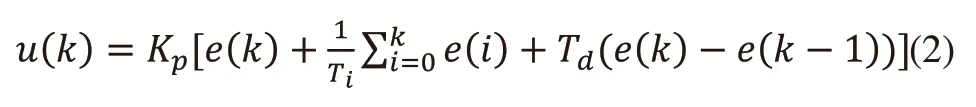
根據式(2)計算u（k-1），并令Δu（K）=u（k）-u（k-1）可得：

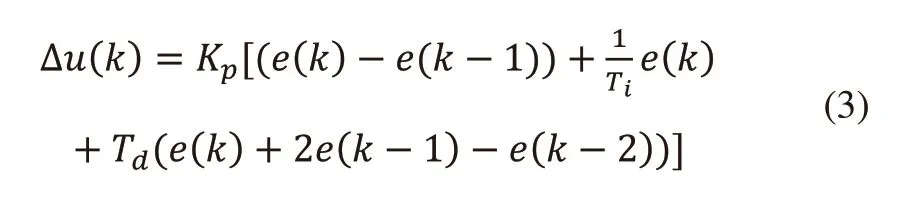
式(3)即為增量式PID算法表達式，適用于自身帶有積分記憶元件的被控對象，該控制算法的第k次輸出值Δu（k）只與于控制系統第k、k-1、k-2次的輸入信號有關，并對其分別進行了加權，這有利于降低處理器計算負擔且不易出現積分飽和現象，只在需要時進行輸出限幅[1]。

2 RBF神經網絡介紹

徑向基函數（RBF-Radial Basis Function）神經網絡是J.Moody在80年代末提出的一種神經網絡[2]，是以函數逼近理論為依據的一種全連接單隱層的三層前向神經網絡（FFNN）[3]，它包括一個輸入層，一個隱含層和一個輸出層。目前認為其可以逼近任意連續函數[2]。

RBF神經網絡的激活函數為高斯（Gaussian）核函數，高斯核函數在局部范圍內為非零值，因此RBF神經網絡為局部逼近的神經網絡[4]。RBF神經網絡的學習速度相對較高，可以滿足實時控制。且其對于訓練樣本的依賴性和要求不高，現代工業控制通常采用RBF網絡與其他常規控制算法相結合，此類控制系統通常具有相當的精度、自適應性和魯棒性[5]。

3 基于RBF辨識網絡的自適應PID控制

3.1 RBF辨識網絡

當前許多領域都是以數學模型為依據來確定最終的控制決策，這可以有效保證控制決策的科學可靠[6]。但收卷機張力控制系統統較為復雜，難以經過理論分析獲得數學模型，因此采用RBF神經網絡辨識系統利用現場實驗來獲取數學模型以及估計參數，為相關實驗提供理論支撐[7]。

RBF辨識網絡在運算時是按照前向或反向傳播過程組織的，下面將對這兩種過程進行敘述。

1）前向傳播過程。

設RBF神經網絡的系統辨識結構設計n-m-1網絡結構，激活函數選擇高斯函數，設輸入層有n個節點，即其中輸入為：

hj為隱含層m個節點中第j個神經元的輸出，表達式為：

cj=cj1，cj2，cj3，…，cjn，cj為第j個節點的中心向量。

b=[b1，b2，b3，…，bm]T，bj為第j個節點的基寬參數且為大于0的數值。

w=[w1，w2，w3，…，wm]T，w為網絡的權值。

RBF神經網絡前向傳播的輸出為：ym（k）=w1h1+，w2h2+…+wmhm。

2）反向傳播過程

梯度下降法具有形式簡單、初始效率較高[8]、局部尋優效果良好等優點[9]，因此采用梯度下降法作為訓練算法。

設RBF神經網絡辨識系統的輸出誤差為e（t），表達式為e（t）=y（t）-ym（t）。其中y（t）為系統實際輸出，ym（t）則為辨識模型實際輸出。同時取辨識誤差指標為E（t），表達式為式(4)。

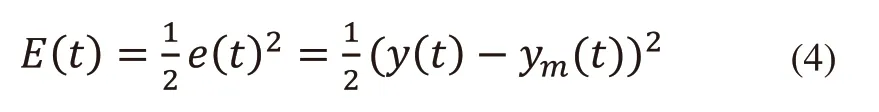
1）權值大小按照式(5)進行調節：

2）隱藏層節點基寬參數按照式(6)進行調節：

3）隱藏層中心向量按照式(7)進行調節：

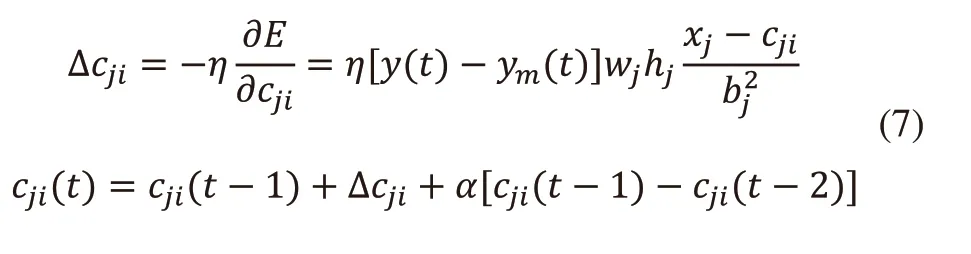
Jacobian信息是反映了RBF網絡辨識所得對象的輸出對輸入的敏感度，其辨識算法如式(8)所示。

3.2 基于RBF系統辨識的自適應PID控制器原理及其步驟

基于RBF系統辨識的自適應PID控制器的原理是使用基于RBF神經網絡的辨識系統對收卷機張力控制系統進行在線辨識，然后根據得到的辨識系統對增量式PID參數進行在線整定。

本文中辨識系統的輸入量為系統偏差、張力控制系統輸入量以及張力控制系統輸出量。在運行過程中辨識系統對張力控制系統進行學習和逼近，使用辨識系統的Jacobian信息來實現對PID參數的整定。RBF神經網絡自適應PID控制的結構如圖2所示。

圖2 基于RBF系統辨識的自適應PID控制結構圖

圖2中增量式PID算法中增量表達式為式(9)，控制率為式(10)。

其中Kp、Ki、Kd為PID可調參數，且：

性能指標函數為式(11)所示。

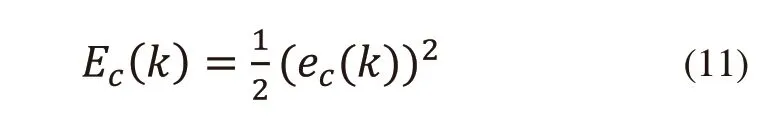
使用梯度下降法對PID參數進行調整，下述三式即為其參數變化量的計算方法。其中ηc為學習率。

PID參數的更新算法為：

由于辨識模型的未知性，因此需做近似處理[10]，取RBF網絡的第一個輸出x1為uk即x1=uk則：

假設欲辨識的非線性系統結構參數已知，則基于RBF神經網絡的自適應PID控制器結構如圖4所示，則其運行步驟如下：

1）確認RBF神經網絡結構為n-m-1，其中輸入參數數量為n，隱含層節點數為m，并確認中心向量、基寬向量、權值向量、學習速率、動量因子初始值。設置PID算法的參數初始值Kp（0）、Ki（0）、Kd（0），以及學習率ηc。

2）接收輸入向量，使用式(9)、式(10)計算被控系統輸入u（t），計算辨識系統輸出ym（t），采樣系統實際輸出y（t），利用式(4)計算辨識模型取辨識誤差指標為E（t）。

3）將得到誤差指標E（t）值，聯立式(5)、式(6)、式(7)計算網絡參數中心向量、基寬向量、權值向量的更新量。

4）使用y（t）、r（t）計算性能參Ec（k），聯立式(13)計算Jacobian信息，使用式(12)計算PID參數更新量。

5）使用得到的的更新量更新辨識系統以及增量PID控制系統參數。

6）將ec（t）與設定的偏差值對比，判斷結束程序或返回步驟2）繼續（t+1）次運行。

4 基于RBF辨識網絡的自適應PID控制策略仿真

基于RBF辨識系統的自適應PID控制算法屬于智能PID算法，而現階段張力控制系統常用的張力控制策略依舊是常規PID控制，下面將通過仿真進行兩者性能對比。

4.1 響應及調整性能對比

結合收卷機張力控制系統的常用模型對傳遞函數為式(14)的被控系統進行控制。其中兩者初始參數由實驗得到，而智能PID控制器的辨識系統使用3-6-1結構，辨識系統學習率為0.5，PID參數學習率ηc使用動態學習率，以此避免后期系統震蕩，且初始值設為0.1，動量因子為0.01。

對智能PID控制器與常規PID控制器分別輸入一個階躍信號，并在50秒時再對兩者分別給與一個干擾信號，使用MATLAB進行仿真，結果對比如圖3所示。

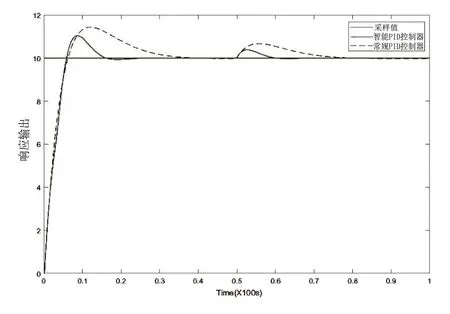
圖3 智能PID控制器與常規PID控制器仿真曲線

根據仿真結果可知，智能PID控制器響應曲線的超調量較小，回穩較快，較常規PID控制器有著更強的適應性和魯棒性。在穩定狀態受到干擾時，智能PID控制器的波動幅度較小，調整較快，即智能PID控制器在性能上優于常規PID控制器。

4.2 跟蹤性能對比

繼續使用上文的非線性被控系統，并使用智能PID控制系統和常規PID控制器分別進行控制。被跟蹤信號表達式如式(15)所示。RBF神經網絡選取3-8-1結構。跟蹤結果如圖4所示。

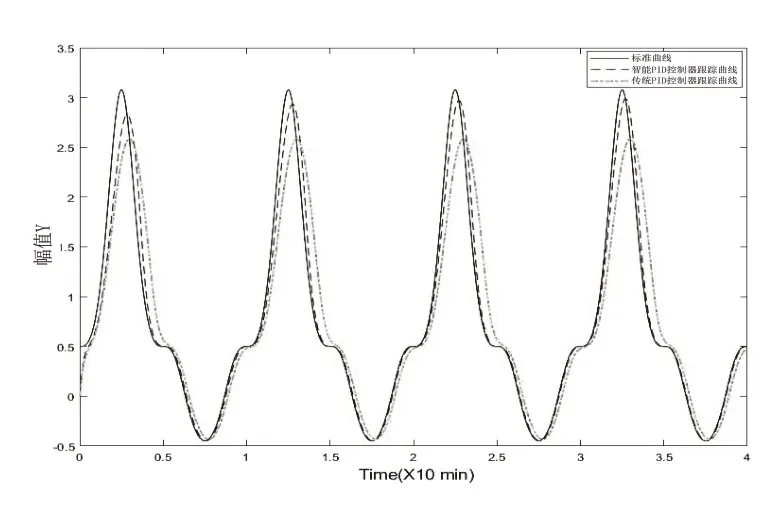
圖4 智能PID控制器與常規PID控制器仿真曲線（2）

由圖4可知，智能PID控制器的跟蹤能力不管在調整速度還是跟蹤精度方面均優于常規PID控制器。在調整過程中幾乎無超調，具有良好的控制精度和效率，而且隨著仿真的持續進行其正在不斷接近被跟蹤系統。而圖5則更明顯的反映了智能PID控制器的自學習和自調整能力，隨著仿真時間的增加被控系統的輸出正在明顯逼近被跟蹤信號，兩者之間的誤差越來越小，甚至幾乎重合。

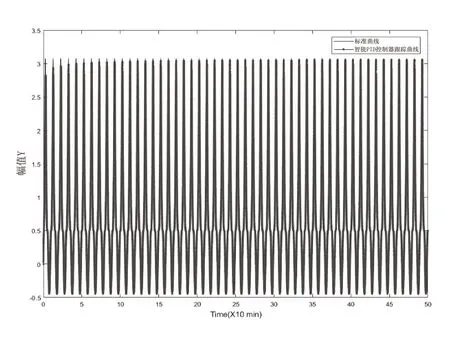
圖5 智能PID控制器的自學習曲線

根據仿真結果，可以明顯看出智能PID控制器在響應、調整性能和跟蹤性能兩方面均優于常規PID控制器，且具有一定的自學習能力。

5 現場測試

現場測試在本單位已經進場施工的某市6.6mBOPA同步拉伸生產線進行，試驗平臺采用北自所自研6.6m高速雙工位翻轉式收卷機，使用常規PID控制與智能PID控制分別對量產合格薄膜進行三次完整收卷，其中收卷機實時張力標準值使用錐度張力函數計算。收卷機張力控制系統工作過程如圖6所示，其中收卷電機使用轉矩模式。

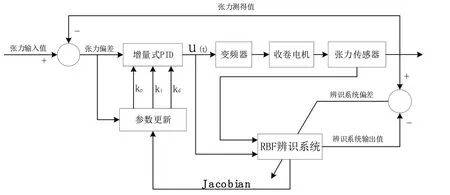
圖6 收卷機張力控制器內部結構圖

張力傳感器最終測得的張力隨卷徑變化結果如圖7所示，可以看出智能PID控制張力與標準值偏差較小，且隨著收卷持續進行，張力偏差不斷減小，說明具有相較于常規PID收卷其具有較強自適應性和一定的自學習能力。

圖7 收卷張力曲線對比

6 結語

本文簡要介紹了常規PID控制與RBF神經網絡，并將基于RBF的辨識系統與PID控制相結合設計了智能PID系統，通過試驗和仿真證明了該系統較于傳統PID控制在收卷機張力控制方面具有良好的自適應和自學習能力。在一定范圍內提高了生產質量。