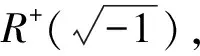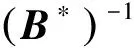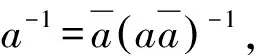具有奇異值分解性質的代數的等價定義

戴 建 宇

(湖南第一師范學院數學與計算科學學院,湖南長沙410205)

0 引言

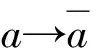
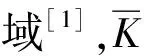
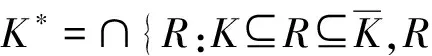
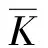
一個形式實域F如果滿足條件F2+F2=F2, 則稱它為一個Pythagorean域。Galois序閉域是一個有序域[1]與Pythagorean域[2],但是Galois序閉域一般不是實閉域[3]。

因為每個形式實域的特征為0,所以Galois序閉域的特征為0。

筆者在文獻[4]研究的基礎上討論了具有SVD性質的代數R的一些不同的等價定義和Galois序閉域的一些性質。

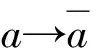
Galois序閉域在具有SVD性質的代數的結構中起著重要的作用, 文獻[2，8-10]已經給出了Galois序閉域的一些重要性質, 下面我們進一步討論。

1 基礎知識

引理 1[4](極分解定理) 設R為一個具有SVD性質的代數,A∈Rm×n,則A有極分解

A=PU。

(1)

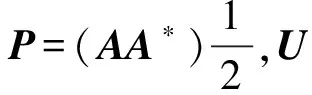
由C上表示矩陣的性質(參見文獻[6-7]), 不難證明公式(1)。

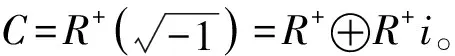
A=QC+RCi。

(2)

并且A=0的充要條件是Q=R=0。

引理 3R是一個具有SVD性質的代數的充要條件：R是一個具有主軸性質的代數。

2 相關結果

由文獻[4]得到具有SVD(奇異值分解)性質的代數的結構定理。

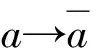
(1)R為一個具有奇異值分解(SVD)性質的代數；

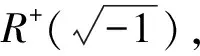
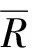
(a)R為一個Galois序閉域；

(b)R的任一個真Galois擴域不是形式實域；

(c)R的任一個真正規擴域不是形式實域；

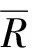
(e)R上每個對稱矩陣在R上相似于對角矩陣；

(f)R上每個對稱矩陣在R上正交相似于對角矩陣。

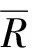
由文獻[4]的引理3, 我們有(a)?(e)?(f)。證畢。

推論1 設R為一個Galois序閉域, 則R是有唯一序的有序域。

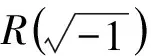
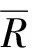
3 具有SVD性質的代數的等價定義

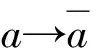
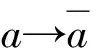
(a)R為一個具有SVD性質的代數；

(b)R具有主軸性質,即R上每個自共軛矩陣酉相似于F上對角矩陣；

(c)R上每個自共軛矩陣相似于F上對角矩陣；

(d)對于R上每個非零矩陣A,A*A酉相似于某個非零對角矩陣D, 并且D的主對角元素均為F中元素的平方；

(e)R上一個正定自共軛矩陣與一個自共軛矩陣的乘積可以相似于F上對角矩陣；

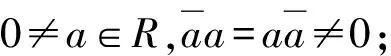
(g)R為一個p除環[13], 并且R+為一個Galois序閉域(作為R的子域)。

由于定理3的證明篇幅較長,我們將它分成兩部分來證明。

證明：由文獻[4]的引理3與引理6及其證明和定理1, 顯然，充分性成立。下面證明必要性。

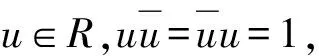
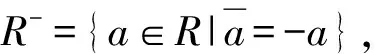
(3)

因此，有

R=R+⊕R-。

(4)

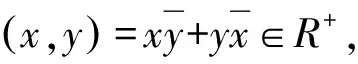
如果R-≠R+i, 則存在x0∈R-，使得

(5)

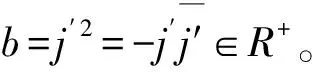
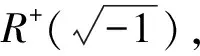
由上述證明與定理1可知R是一個具有SVD性質的代數。證畢。

定理3的證明:由引理3知(a)?(b)。顯然，我們有(b)?(c)。若(c)成立,由引理3的證明方法(只需將酉矩陣換成可逆矩陣),同理可知(a)成立。因此(a)?(b)?(c)。

(6)

則由條件與體上矩陣秩的理論可知:存在酉矩陣U，使得

(7)

其中0≠λ1∈F。經過矩陣計算不難得到

(8)