支持向量機的電力故障檢測方法研究

王振國，賈 飛，余 洋

(內蒙古電力(集團)有限責任公司烏海電業局，內蒙古 烏海 016000)

0 引言

隨著電網系統的負荷持續增長以及電網規模的不斷增容，影響電網穩定運行的不確定因素也日漸增多。電網故障檢測是保障電力系統正常、有效運行的關鍵技術。相對于傳統電網，智能電網可以借助人工智能和機器學習技術，保障電力系統的穩定運行。支持向量機[1](support vector machine,SVM)是一種優秀的機器學習模型。為構造一個最優分類超平面，SVM以最大間隔為優化目標，實現了學習模型的結構風險極小化。它在處理小樣本數據方面性能卓越。同時，它的全局最優解可通過優化一個凸二次規劃問題來獲得。SVM的優勢受到了學術界與工業界的關注，并且已被成功地應用了到各大領域[2-4]，比如故障檢測、場景識別、金融信用、生物識別等。

為解決SVM在處理異構數據分布學習問題上性能較差的不足，Jayadeva等[5]在機器學習領域期刊TPAMI上提出了非平行支持向量機學習范式，并在此基礎上給了一個雙胞支持向量機(twin support vector machine,TWSVM)模型。相對SVM，TWSVM模型在處理“交叉型”數據問題上表現出卓越的泛化能力，并具有更好的學習效率。因此，TWSVM得到了國內外很多學者的青睞，并后續提出了很多優秀的模型。例如，雙胞界限支持向量機(twin band support vector,achine,TBSVM)[6]，最小二乘雙胞支持向量機(least square twin support vector machine,LSTSVM)[7]，雙胞參數間隔支持向量機(twin parametric-margin support vector machine,TPMSVM)[8]，中心雙胞參數間隔支持向量機(centroid parametic-margin support vector machine,CTPSVM)[9]，多標簽支持向量機(multi-label twin support vector machine,MPSVM)[10-11]等模型。

CTPSVM[9]是近年來被提出的一種非平行機器學習方法，擁有優秀的泛化能力。然而，CTPSVM故障檢測模型的解需要通過求解二次規劃問題來獲得，并不適合處理大規模學習問題。為解決上述問題，受最小二乘法LSTSVM模型[7]啟發，將提出一個新的最小二乘中心雙胞參數間隔支持向量機(least square centroid twin parametric-margin support vector machine,LSCTPSVM)故障檢測模型。該模型旨在使得每個類的樣本盡量聚在它所對應的每個超平面的附近，同時其超平面盡量遠離樣本中心點。對于CTPSVM模型，該模型擁有如下特點：將CTPSVM模型的不等式約束松弛到等式約束，并引入最小二乘法損失函數來懲罰犯錯樣本；為提高模型的泛化能力，額外的正則項被引入到LSCTPSVM模型中，保障了模型解的唯一性；相對于CTPSVM模型的解需要借助于二次規劃的對偶問題來間接的求得，LSCTPSVM模型可直接使用簡單而高效的線性方程組系統來獲得其原始問題的最優解。在線性和非線性分類問題上，本文提出的LSCTPSVM擁有與CTPSVM相近的泛化能力，但具有更高效的學習效率。

1 中心雙胞參數支持向量機

本文采用如下的符號約定：所有的向量都為列向量；上標“T”表示轉置；I表示單位矩陣；0和E分別表示全0向量和全1向量。考慮n維實空間Rn中的二分類學習問題[1]，給定訓練數據集為:

T={(x1,y1),(x2,y2),...,(xt,yt)}

(1)

式中:l為訓練集的規模；x∈Rn為第i個訓練樣本點；yi∈{-1,+1}為訓練樣本點所對應的類別標簽。

此外，記I+和I-分別為屬于正類和父類的樣本集合索引，其規模分別為l1和l2。

CPTSVM模型[9]的核心思想是，在特征空間中，尋找一對最優的非平行超平面。

(2)

使得每個超平面fk(x)盡量將當前第k類的樣本劃分為同一側；另一方面，樣本中心盡量在另一側遠該超平面。為實現上述目標，CPTSVM模型[9]優化如下原始問題：

(3)

(4)

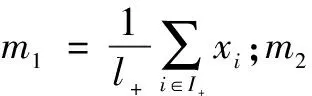
類似于SVM，為求解問題和的解，首先將它們轉換為對偶問題：

(5)

(6)

然后，當求得對偶問題的最優解α1和α2，可推得原始問題的解：

(7)

(8)

值得注意的是，在CTPSVM模型中，b1和b2的最優解不能直接由對偶解α1和α2計算得到，而是必須通過支持向量與ω1和ω2間接計算得到。對于新樣本x的預測，其類別的判別依據如以下決策函數：

Classx=f1(x)+f2(x)=

sign[(ω1+ω2)Tx+(b1+b2)

(9)

2 最小二乘中心雙胞參數間隔支持向量機

CTPSVM模型的解需要通過求解二次規劃問題來獲得，并不適合處理大規模學習問題。為此，受最小二乘法LSTSVM模型[7]啟發，提出LSCTPSVM模型，旨在選擇一對最優的非平行超平面：

(10)

使得每個類的樣本盡量聚在它所對應的每個超平面的附近，同時該超平面盡量的遠離樣本中心點。為實現上述目標，首先將CTPSVM的原始問題和中的L1模的松弛變量ξ和η轉換為L2模，同時將不等式約束。轉換為等式約束，構造如下的經驗風險函數：

(11)

(12)

式中:c1,c2,μ1,μ2>0為懲罰參數，用于調節損失函數式和中各項損失的權重。

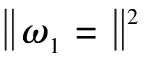
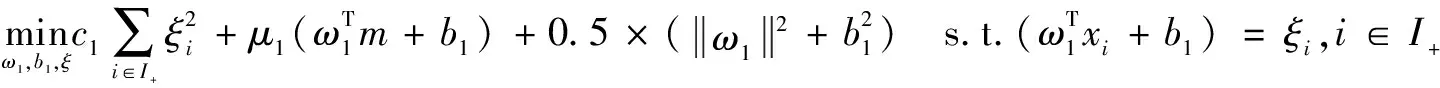
(13)

(14)

接下來，將對LSCTPSVM模型給出解釋。首先，討論和分析優化問題。LSCTPSVM模型的幾何解釋如圖1所示。

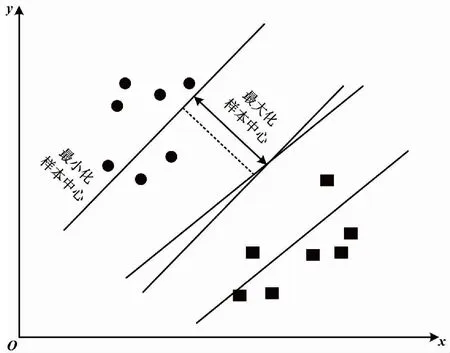
圖1 LSCTPSVM模型的幾何解釋

①第1項和約束條件實現了正類樣本的經驗風險函數。這里使用最小二乘法準則度量正類樣本離超平面的距離。對于偏離超平面的正類樣本點，引入松弛變量ξi度量其誤差。極小化這項期望所有正類樣本能聚在正類超平面附近。

②極小化第2項是希望樣本的中心點m盡量在超平面f1函數值為負的半空間，且距離超平面f1越遠越好。f1(m)越小，則代表正類與負類中的間隔越大，那么模型的泛化能力將會越強。

3 模型優化與求解

將優化問題的等式約束代入到目標函數中，可將問題和轉換為如下的無約束的二次規劃問題：

(15)

(16)

對于無約束優化問題，其最優解可以通過對J1(ω1,b1)關于變量ω1和b1求偏導：

(17)

(18)

整理可得:

(19)

(20)

同理，對于無約束優化問題，其最優解可以通過J2(ω2,b2)對關于變量ω2和b2求偏導：

(21)

(22)

整理式(21)和式(22)，得:

(23)

(24)

優化問題(13)、(14)及其最優解可通過求解式(20)、式(21)和線性方程組獲得。相對于CTPSVM通過對偶問題的二次規劃間接獲得最優解，LSCTPSVM模型可通過求解線性方程組問題來直接優化原始問題獲得最優解。對于新樣本x的預測，其類別的判別依據如下決策函數：

Cx=f1(x)+f2(x)=sign[(ω1+ω2)Tx+(b1+b2)]

(25)

4 試驗結果分析

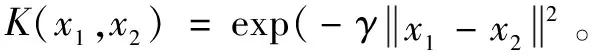
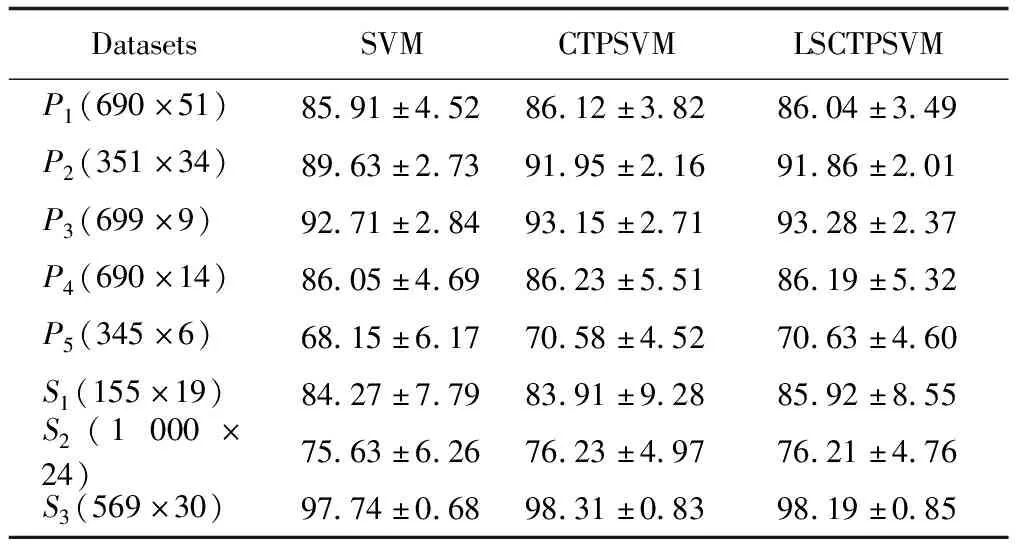
表1 線性各分類器在UCI數據集上的分類準確率對比

表2 各非線性分類器在UCI數據集上的分類準確率對比

表1和表2分別給出了各模型在UCI數據集上的線性和非線性的平均分類準確率。試驗結果表明：本文所提出的LSCTPSVM模型，具有與CTPSVM相近的分類性能。比如對于線性和非線性情況，LSCTPSVM在8個UCI數據集中，分別有3個和4個數據集的分類性能超過CTPSVM。從分類結果的穩定性上看，在大部分數據集，LSCTPSVM的分類方差比CTPSVM的要小，主要原因是在LSCTPSVM模型中引入了額外的正則項b2，可以直接得到模型的最優解，進而提高了模型的穩定性。此外，LSCTPSVM模型在線性和非線性性能在大部分的數據上都超過了SVM。各線性和非線性分類器在UCI數據集上的學習時間比較如圖2所示。

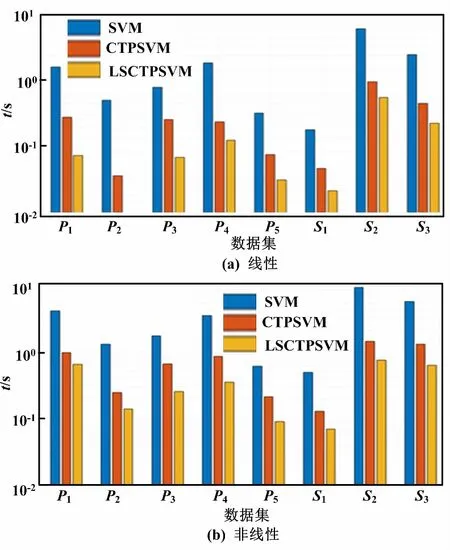
圖2 各線性和非線性分類器在UCI數據集上的學習時間比較圖

試驗結果表明：LSCTPSVM模型的訓練時間最短，其次是CTPSVM，最慢的是SVM。這是由于LSCTPSVM通過直接優化原始問題，只需要求解一組線性方程組來獲得最優解；而SVM和CTPSVM的最優解需要通過求解二次規劃問題來獲得，時間復雜度較高；同時，SVM優化一個較大的二次規劃問題，而CTPSVM和LSCTPSVM將較大的優化問題分為兩個較小規模的問題。上述線性和非線性試驗結果驗證了LSCTPSVM模型的有效性。

5 結論

由于故障檢測模型CTPSVM的解需要通過求解二次規劃問題來獲得，并不適合處理大規模學習問題。為此，受最小二乘法LSSVM模型啟發，本文提出了一個新的最小二乘中心雙胞參數間隔支持向量機模型，簡稱LSCTPSVM。該模型旨在使得每個類的樣本盡量聚在它所對應的每個超平面的附近，同時該超平面盡量遠離樣本中心點。本文的主要貢獻是：①在LSCTPSVM模型中，首先將CTPSVM模型的不等式約束松弛到等式約束，并引入最小二乘法損失函數來懲罰犯錯樣本;②為提高模型的泛化能力，額外的正則項被引入到LSCTPSVM模型中，進而保證了模型解的唯一性;③相對于CTPSVM模型的解需要借助于二次規劃的對偶問題來間接的求得，LSCTPSVM模型可直接使用簡單而高效的線性方程組系統來獲得其原始問題的最優解。最后，在公共數據集和電網遙感數據集上，驗證了LSCTPSVM故障檢測模型的有效性[13]。