薄壁空心墩有效剛度試驗研究

邵長江，韋 旺，孫南昌，漆啟明，胡晨旭，佐 雪

(1.西南交通大學 土木工程學院，四川 成都 610031；2.陸地交通地質災害防治技術國家工程實驗室，四川 成都 610031)

有效剛度是分析橋墩動力特性的關鍵物理量，同時有效剛度的使用也為建立非線性橋墩的雙折線簡化分析模型奠定了基礎[1-2]。通常取屈服點對應的剛度作為橋墩有效剛度，故計算橋墩有效剛度的關鍵是屈服點的確定。眾多學者、規范根據能量等值原則或Park法等定義橋墩有效剛度。Mehanny等[3]認為隨著軸壓比的增大，有效剛度最大值可以取到0.9倍的初始剛度。Paulay等[4]則認為，軸壓比大于0.5時，混凝土墩有效剛度最大值取為0.8倍的初始剛度；軸壓比小于-0.05時，取為0.4倍的初始剛度，軸壓比在-0.05～0.5之間采用線性插值法取值。基于120個墩柱的試驗結果，文獻[5]給出軸壓比小于0.2時，有效剛度最小值取為0.2倍的初始剛度。Panagiotakos等[6]基于1 000個擬靜力試驗結果，認為有效剛度均值為毛截面剛度的0.2倍。僅考慮軸壓比影響的公式其形式簡單、便于工程應用等，得到文獻[7-9]的認可。除軸壓比外，文獻[10-12]研究得出剪跨比對橋墩有效剛度的影響不容忽視，并發展了同時考慮軸壓比和剪跨比影響的有效剛度模型。

文獻[13-19]認為有效剛度會受到多重因素的同時影響，進而提出了考慮多重因素的計算模型。文獻[2]根據能量相等原理，通過把實際彎矩-曲率曲線等效為理想彈塑性彎矩-曲率曲線，來確定墩柱截面的等效屈服彎矩My和等效屈服曲率φy，并定義有效剛度為等效屈服彎矩與等效屈服曲率之比。該模型能同時反映橋墩開裂及鋼筋首次屈服時的工作狀態，已被諸多規范采納[20-22]。Kumar等[13]認為軸壓比、縱筋率、剪跨比及混凝土抗壓強度為其主要影響參數。文獻[14-18]在綜合考慮多重因素的基礎上，給出了不同形式的有效剛度計算公式。文獻[14-16]等認為縱筋率對橋墩有效剛度也有較大影響。Berry等[14]給出考慮軸壓比、剪跨比及縱筋率等影響的橋墩有效剛度計算模型。Khuntia等[15]則給出考慮縱筋率、軸力偏心距及軸壓比等影響的計算模型。Elwood等[17]認為墩頂位移能力受到彎曲、剪切及縱筋滑移位移等多種因素影響，提出了考慮軸壓比、剪跨比及縱筋直徑等的有效剛度計算模型。受文獻[17]影響，文獻[11，16，18]從彎曲、剪切和縱筋滑移變形等三方面出發分析有效剛度的主要影響參數，認為除軸壓比和剪跨比影響外，滑移變形也是有效剛度的主要控制因素，并通過引入參數來考慮縱筋滑移變形對有效剛度的影響。

基于理論及試驗對橋墩有效剛度展開了大量研究，取得的諸多成果已經納入有關設計規范，并應用于工程實際。然而對于鐵路橋墩，我國現行GB 50111—2009《鐵路工程抗震設計規范》[23]則取鋼筋首次屈服時作為橋墩的屈服點，鋼筋首次屈服對應的橋墩有效剛度則少有研究。另外，相比相同外部尺寸的實心墩，鐵路薄壁空心墩具有節省材料、減小恒載及一定程度上降低地震慣性力等優點，因而廣泛應用于山區高墩大跨橋梁中。空心墩和實心墩的構造、配筋方式(縱筋、箍筋、拉筋)有明顯不同，兩者約束混凝土效應差異顯著，致使墩身裂縫開裂行為和損傷模式不同，因而相同外部尺寸的薄壁空心墩與實心墩剛度差異較大[24-25]。基于實心墩得出的既有成果對空心墩的適用性值得質疑。為此有必要在深入研究有效剛度影響因素的基礎上，結合理論和試驗成果，系統梳理現有計算公式，為鐵路薄壁空心墩尋求最佳的有效剛度計算模型。論文選取軸壓比、配箍率為設計變量，通過5個大比尺模型擬靜力試驗，研究鐵路薄壁空心墩有效剛度，對比既有文獻成果，分析現有公式估算薄壁空心墩有效剛度的有效性及合理性。

1 既有研究成果

已有研究表明，墩頂屈服位移主要由沿墩身的彎曲、剪切變形及固端縱筋滑移(稱為位移三分量)的耦合效應引起[13,19]，而影響位移三分量貢獻的因素有：軸向荷載、混凝土彈性模量、有效截面面積、墩高、縱筋屈服強度、縱筋直徑、配筋率、配箍率、約束混凝土效應等。因此，基于屈服點的有效剛度影響因素相當復雜，既有研究成果給出形式多樣計算公式，根據影響因素的依次增多，將既有模型分為以下三類，見表1～表3。表中，μ為軸壓比;λ為剪跨比；My為等效屈服彎矩；φy為等效屈服曲率；L為構件有效高度；D為構件截面寬度；db為縱筋直徑；ρl為縱向配筋率；fc′為混凝土抗壓強度；fy為鋼筋屈服強度；e為軸力偏心距。

表1 僅考慮軸壓比影響的計算模型

2 試驗研究

為尋求圓端薄壁空心墩的有效剛度估算公式，論文選取軸壓比和配箍率作為控制變量，設計5個大比尺圓端型薄壁空心墩，進行擬靜力加載試驗。根據試驗現象和試驗結果，對比分析設計參數對圓端薄壁空心墩有效剛度的影響，結合有效剛度實測值和各有效剛度公式的計算值，探討既有計算公式對圓端薄壁空心墩的適用性。

2.1 模型設計

變截面圓端薄壁空心墩試件采用C35混凝土，縱筋均為HRB400φ12，箍筋及拉筋為R235φ6。模型設計參數見表4，各構件的剪跨比統一為6.23，薄弱位置為2-2截面(計算剪跨比的位置)。模型尺寸及配筋見圖1，加載制度見圖2。

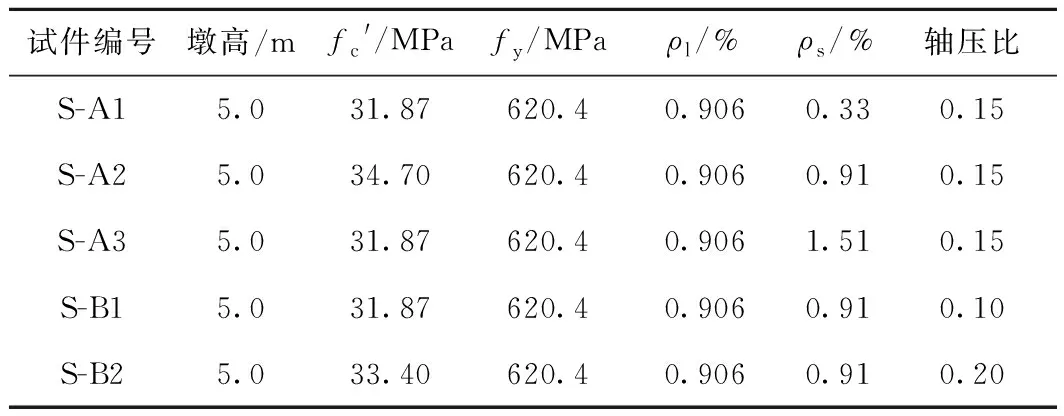
表4 模型設計參數

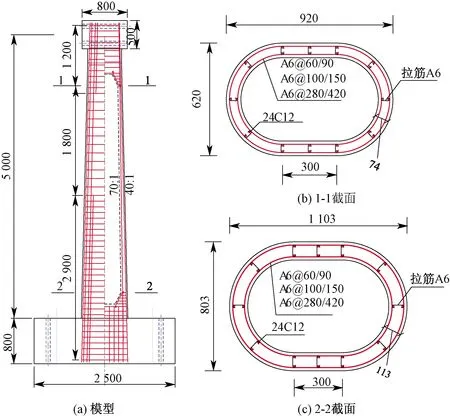
圖1 模型尺寸及配筋(單位：mm)

圖2 加載制度

2.2 試驗結果分析

根據試驗結果，5個試驗墩均發生彎曲破壞，墩身微裂紋較密，貫穿裂縫較分散。極限狀態下，變截面處混凝土裂縫較寬，受壓區混凝土壓潰現象顯著；角隅處受拉區縱筋拉拔現象不明顯。

加載試驗過程中，在距墩底大約10 cm處出現第一條微裂縫，隨著荷載的繼續增加主裂縫相續出現；相鄰裂縫之間混凝土的拉應力不超過抗拉強度時，不再產生新裂縫，而原有裂縫斜向繼續延伸。外荷載水平較高時，變截面倒角附近受拉鋼筋達到屈服強度、受壓區混凝土壓潰脫落。屈服鋼筋的應力增幅小于變形增加的速度，最終導致橋墩最寬裂縫處縱筋拉斷[6,25]。上述試驗過程中，縱筋首次屈服是由彎曲引起，此時剪切變形及縱向鋼筋滑移效應并不顯著，故墩頂位移為彎曲變形所致。

確定屈服點是有效剛度定量的關鍵，通常采用能量等值法和Park法等來確定構件的屈服點。能量等值法是根據P-M-φ曲線通過面積(能量)等效的原則，將M-φ曲線等效為雙折線，得到屈服彎矩及屈服曲率見圖3。Park法基于力-位移曲線確定屈服點見圖4。此外，鋼筋首次屈服是判斷橋墩是否進入塑性變形的關鍵點，故GB 50111—2009《鐵路工程抗震設計規范》采用截面最外側鋼筋首次屈服時作為橋墩的屈服點，根據鋼筋首次屈服確定的薄壁空心墩有效剛度約為等效屈服點確定的1.40倍，見表5。

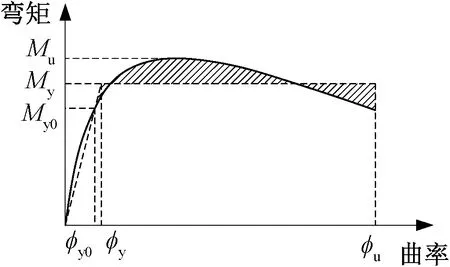
圖3 能量等效法

圖4 Park法

表5 有效剛度試驗結果

針對鐵路空心墩，以GB 50111—2009《鐵路工程抗振設計規范》指定截面最外側鋼筋首次屈服對應的割線剛度作為橋墩的有效剛度，圖1中2-2截面剛度為初始剛度，截面剛度實測結果與截面初始剛度之比見表5。有效剛度比受軸壓比及配箍率的影響規律見圖5、圖6。結合試驗結果及綜合分析，以文獻[18]中試驗統計分析得到的橋墩有效剛度模型為基礎，得到圓端薄壁空心墩有效剛度計算公式為

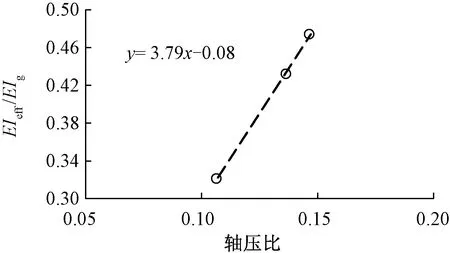
圖5 軸壓比對有效剛度實測值的影響

圖6 箍筋率對有效剛度實測值的影響

(1)

由圖5、圖6可知，圓端薄壁空心墩有效剛度受軸壓比的影響較顯著，且隨軸壓比的增大而增大。雖然箍筋對混凝土的約束效應起到增強截面剛度的作用，但是對于薄壁空心墩來說約束效應相對較弱，因此箍筋對薄壁空心墩有效剛度的影響不是很大。

3 現有公式對比分析

為方便比較現有公式的適用性，試件有效剛度的計算值與實測值之比見表6。S-B2試驗實測軸壓比為0.137，有效剛度根據實測值計算。各公式計算值比較見圖7，兩類結果的比值見圖8。

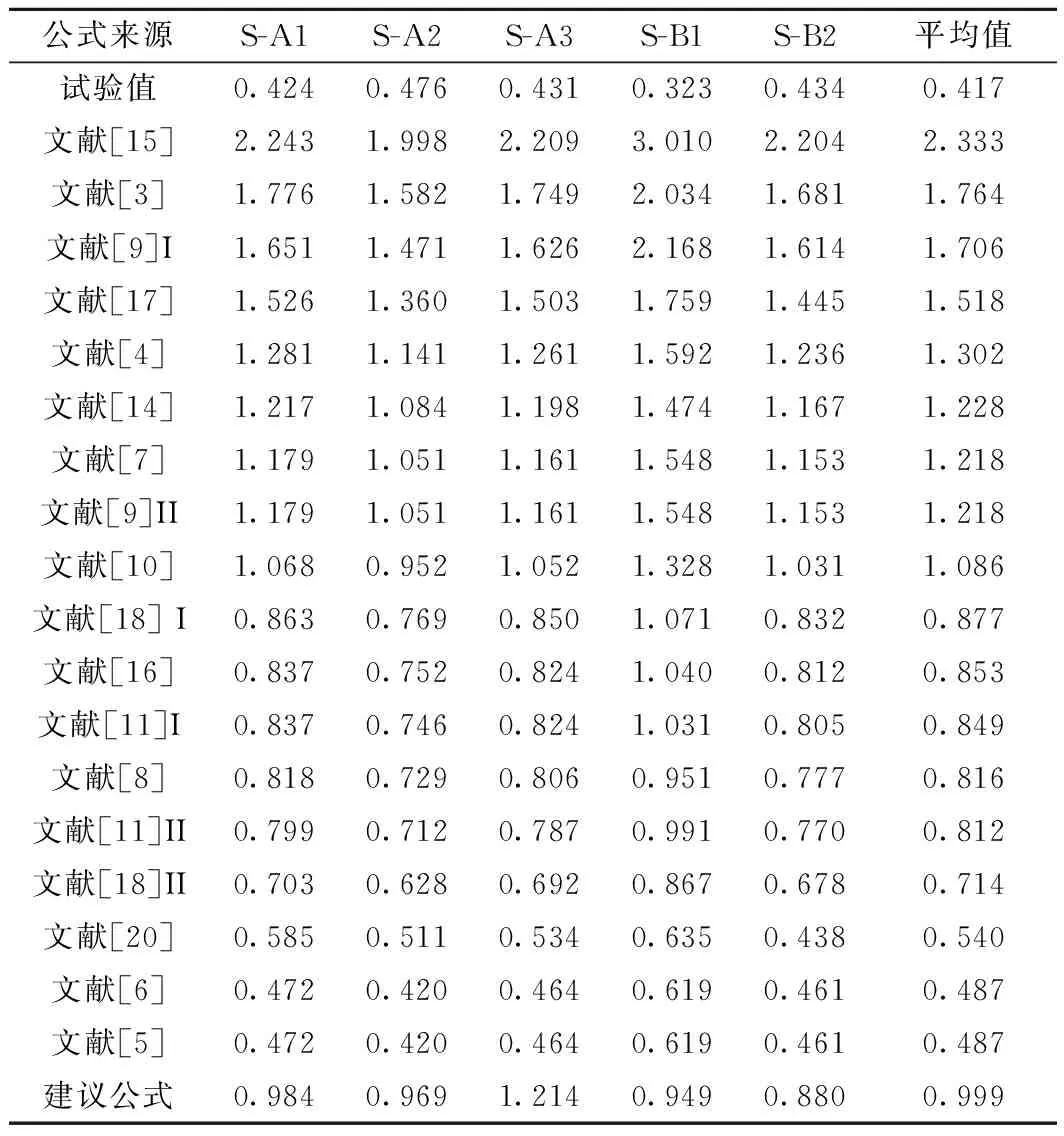
表6 有效剛度公式計算值與試驗值之比

圖7 有效剛度計算值與試驗值比較

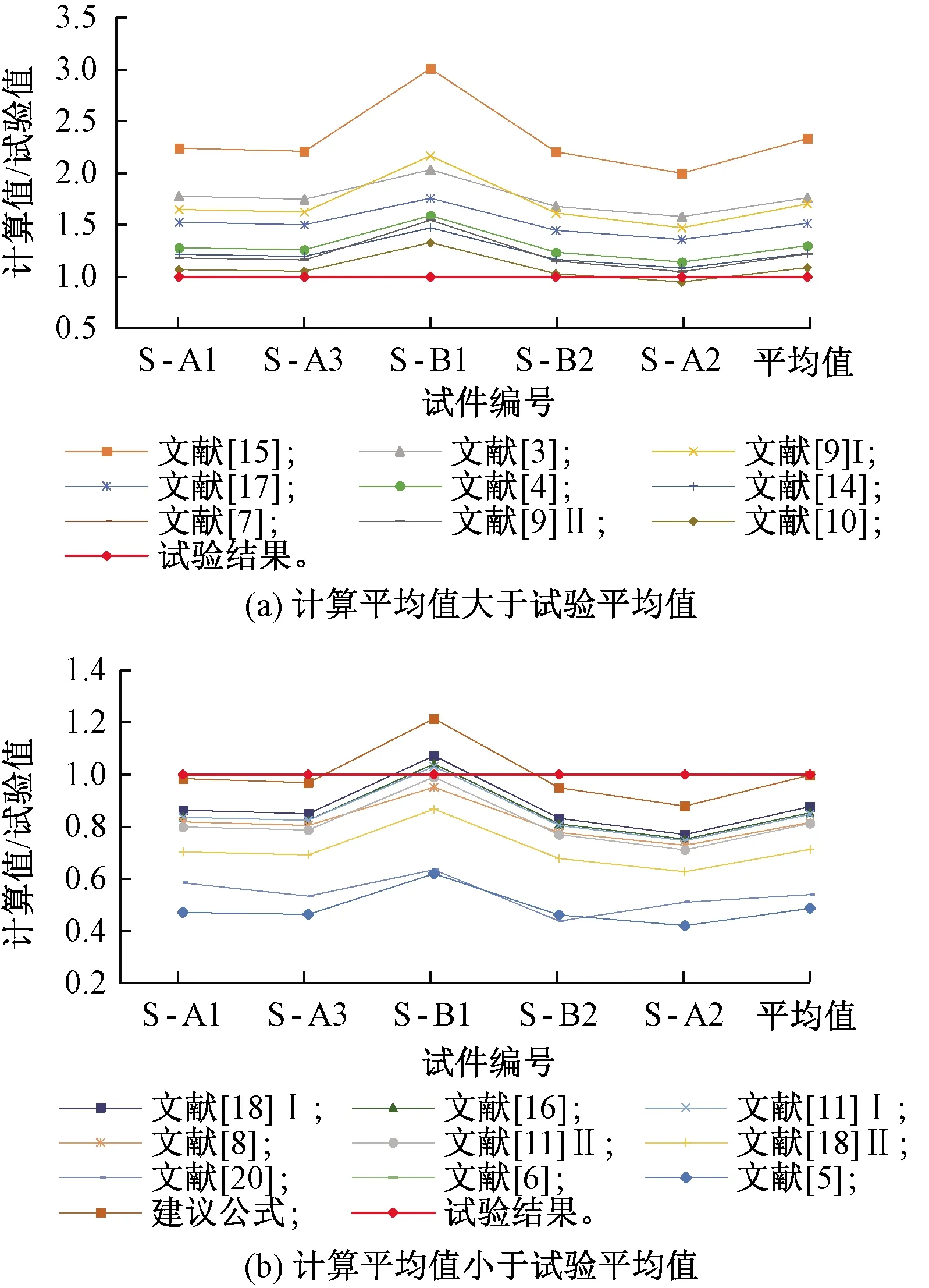
圖8 有效剛度公式計算值/試驗值

由表6及圖7、圖8中圓端空心墩有效剛度估計結果對比分析可知：

(1)設計參數影響規律：由圖7可知，S-B1試驗結果與各公式計算值變化差異較大，但總體上呈現一定規律。由S-B1、S-B2、S-A2的試驗結果可知，除文獻[15]給出相反規律，文獻[5-6,9]有效剛度為定值外，其余公式的計算值與試驗值變化規律基本一致，都是隨軸壓比的增大而增大。由S-A1、S-B2、S-A3的試驗結果可知，當軸壓比不變而配箍率變化時，試驗值一定程度上隨配箍率的增大而增大，而各計算結果幾乎為定值，并未考慮配箍率的影響，這與論文結果有較大差異。同時，與配箍率比較小的S-A1相比、S-B2的試驗值反而比S-A1試驗值大，原因在于S-B2試件混凝土抗壓強度大于S-A1試驗混凝土抗壓強度，有效剛度隨混凝土抗壓強度的增大而增大的趨勢。但現有模型中均未單獨考慮混凝土抗壓強度的影響。

(2)公式合理性：由表6和圖8可知，分析有效剛度計算值與試驗值之比，文獻[5-6，20]、文獻[18]Ⅱ等較大地低估了圓端薄壁空心墩的有效剛度，而文獻[8，11，16]、文獻[18]Ⅰ等的計算值則較為保守，其余現有公式對圓端型薄壁空心墩有效剛度的估計普遍偏高。除文獻[10]外，模型[3-4,7,9,14-15,17]較大程度上高估了圓端薄壁空心墩的有效剛度，計算值均超過試驗值的1.218倍，容易導致不安全的設計結果。相對于低估了圓端薄壁空心墩的有效剛度的結果相比[5-6]，文獻[20]的估計值較為接近試驗值，三者平均比值分別為0.487、0.487和0.540，總體上這種過于保守的估計值會造成實際工程上的浪費等。模型[8,10-11,16,18]及本文公式的計算值與試驗值相對較為接近，平均比值在0.714～1.086之間。

(3)公式適用性：根據表6的結果，盡管文獻[16]的計算結果與試驗實測值比較接近，但是沒有考慮到剪跨比的影響，研究表明有效剛度受剪跨比的影響較為顯著，對于不同剪跨比的試件，該公式是否適用還有待驗證；文獻[8]計算值與試驗值也較為吻合，但其僅考慮軸壓比的影響，這種簡單處理方式，導致其適用性有限；文獻[11]的計算值較接近于試驗值，而與其公式Ⅱ相比，考慮了軸壓比及剪跨比影響的公式Ⅰ計算效果更好，但相對于公式Ⅰ，文獻[10，18]及本文公式的計算值更接近于試驗結果(見圖8)。

綜上所述，文獻[10，18]對于圓端型薄壁空心墩有效剛度的估計效果相對較好，而前者計算值略大于試驗值，會造成不安全的設計結果。而建議公式更適用于估算圓端型薄壁空心墩的有效剛度，偏于保守的估計則可采用文獻[18]的公式Ⅰ。

4 結論

通過分析國內外相關研究成果，系統梳理了現有橋墩有效剛度計算公式，并基于擬靜力試驗結果，探討了圓端型薄壁空心墩有效剛度的影響因素，研究了現有橋墩有效剛度計算公式的適用性。結果表明：

(1)試驗構件均發生彎曲破壞，墩底變截面處損傷嚴重，主干裂縫遍布墩身，側向斜裂縫明顯，構件延性性能較好。

(2)與常規橋墩相比，圓端型薄壁空心墩有效剛度的影響因素大體相同，但受各因素(軸壓比、剪跨比、縱向配筋率、縱筋直徑、縱筋屈服強度、配箍率及混凝土強度等)影響的顯著性有所差異。

(3)文獻[3-4，7，9，14-15，17]的計算結果過于偏高，容易導致不安全的設計結果，文獻[5-6，20]的計算結果過于保守，不太適用于估算圓端型薄壁空心墩有效剛度。

(4)文獻[8,15]的計算效果較好，但其考慮因素過于單一，不大適用于估算圓端型薄壁空心墩的有效剛度。文獻[11]的相對誤差大于15%，也不大適用于計算薄壁空心墩的有效剛度。

(5)文獻[10]、文獻[18]Ⅰ對于圓端型薄壁空心墩有效剛度的估計效果相對較好，文獻[10]的計算值略大于試驗值，容易導致不安全的設計結果。偏保守考慮，則可采用文獻[18]中的公式Ⅰ。

綜合分析，所建議公式更適用于估算鐵路薄壁空心墩的有效剛度。限于模型試驗設計參數及試件加工數量，現有研究尚無法全面揭示各類因素對圓端型薄壁空心墩有效剛度的影響及規律。針對圓端型薄壁空心墩有效剛度的計算公式，仍需更多、更深入的針對性試驗研究。