基于MIC與BiGRU的水電機組振動趨勢預測

畢 揚，鄭 波，張亞武，朱 溪，江亞蘭，李超順

（1.浙江仙居抽水蓄能有限公司，浙江 仙居 317300；2.中國電建集團華東勘測設計研究院有限公司，浙江 杭州 311122；3.國網新源控股有限公司，北京 100761；4.華中科技大學 水電與數字化工程學院，湖北 武漢 430074）

1 研究背景

水電機組作為電網調峰調頻的重要設備，在運行過程中受水力沖擊、機械失效和電磁不平衡等綜合因素的影響，會誘發各種故障與事故。水電機組的振動信號通常能夠反應出機組運行狀態的變化及故障，因此從水電站監測數據中挖掘有效特征，并構建準確的振動趨勢預測算法可以提升機組和電力系統運行的安全穩定性，減少不必要的計劃停機和意外停機［1-4］。

水電機組振動趨勢預測是一個非線性非平穩的序列預測問題，預測方法通常分為物理模型和數據驅動方法兩大類。基于物理模型的方法包括回歸模型，Weibull 分布模型，卡爾曼濾波和粒子濾波等，在預測中得到廣泛應用。文獻［5］提出了一種基于自回歸指數平滑模型的預測方法，其通過日內周期指數平滑實現了短期預測；Kharoufeh 等［6］提出采用馬爾可夫模型來計算不同時刻振動趨勢的分布狀態以實現水電機組振動預測。這些基于物理模型的方法雖取得一定成果，但它依賴于專家的經驗知識來建立數學模型，具有不確定性和不穩定性，并忽視了對影響振動因素的深入分析。相反，數據驅動方法則不需要建立任何精確的預測模型，而是通過學習歷史振動數據變化規律構建數據間的映射關系來實現時序預測，因此受到廣泛關注。

數據驅動方法通常分為數據獲取、特征提取、特征選擇和趨勢預測，特征提取與選擇對振動趨勢預測具有重要影響。傳統的信號處理方法通過提取時域或頻域特征來表達原始數據的物理意義或統計意義，然而對于參數隨時間不斷變化的非線性非平穩信號，針對不同的數據需要設計不同的時域或頻域特征，它不具有普適性。以小波變換和經驗模態分解方法為代表的時頻域分析方法通過時間和頻率的聯合函數對信號分析，可將信號分解為一系列單頻的平穩信號，均具有較好地表征非平穩信號的能力。例如，文獻［7］提出了一種改進的小波閾值函數降噪算法，保留了振動信號突變點信息，并更好的跟蹤原信號特征。文獻［8］通過最優變分模態分解將非平穩振動序列分解為一系列模態函數，實現了各信號分量頻率的分離。然而，并不是所有提取的特征都能夠提供有用的信息，因此，許多指標被提出用來進行特征評價以選出具有代表性的特征。文獻［9］使用單調性、預測性、趨勢性來排除冗余特征，文獻［10］采用Pearson 相關系數來分析特征之間的相關性。這些方法對于特征之間的線性相關性更敏感，卻忽略了非線性相關性，而最大信息系數（Maximal information coeffi?cient，MIC）［11］可以很好地衡量變量間的線性或非線性強度，具有更高的準確度。就預測算法而言，隨著深度學習的發展，其將多層次的非線性低維特征形成更加抽象的高維表示，具有更高的泛化能力和特征提取能力，提高了振動預測的精度和穩定度，已在水電機組壽命預測、故障診斷等方面取得了較好的應用。例如，文獻［12］提出了一種新的基于深度卷積神經網絡（Deep convolution neural network，DCNN）的振動趨勢預測方法。與淺層網絡模型相比，DCNN 具有強大的特征提取能力，但它忽略了水電機組振動信號在時間序列中的聯系。遞歸神經網絡（Recurrent neural network，RNN）的提出很好地解決了時序預測問題，RNN 的神經元可以同時接收自身歷史時刻以及其他神經元的信息，具有記憶性、參數共享的特點，對于序列數據的非線性特征學習具有獨特優勢［13］。但是RNN 具有長期依賴和梯度爆炸或消失的問題。因此，長短時記憶網絡（Long short term memory，LSTM）通過引入門控機制避免了長期依賴問題，但其內部參數較多，而門控循環神經網絡（Gated Recurrent Unit，GRU）則通過減少門控機制使其結構更加優化，減少訓練時間。雙邊門控循環神經網絡（Bidi?rectional gated recurrent unit，BiGRU）則從時間序列數據中提取歷史和未來方向的特征，充分挖掘數據信息，進一步提高了預測精度。

綜上所述，水電機組振動信號波動范圍大，其非平穩性對預測的精度和穩定度的提高有很大的影響。為構造有效的特征集，提高數據的有效性，并建立精確的預測模型，本文提出了一種基于WTD 的信號去噪、基于MIC 的特征選擇、基于BiGRU 網絡的混合預測方法，即WTD-MIC-BiGRU 模型。首先采用小波閾值去噪（Wavelet threshold de-noising，WTD）對原始振動信號進行降噪和濾波處理，以有效區分振動信號中的高頻部分和由噪聲引起的高頻干擾，并對信號進行特征提取和低通濾波；再利用MIC 對振動信號和工況參數進行深層次關聯性分析，挖掘狀態參數與振動信號之間的非線性關系，選出相關性最強的狀態參數作為特征輸入；最后采用BiGRU 網絡建立預測模型進行趨勢預測。實驗結果證明本文提出的模型訓練時間短，泛化能力強，取得了較好的預測結果。

2 基本原理

2.1 方法框架本文預測模型的流程如圖1所示，總體分為在線階段和離線階段兩個階段。其具體建模步驟如下。

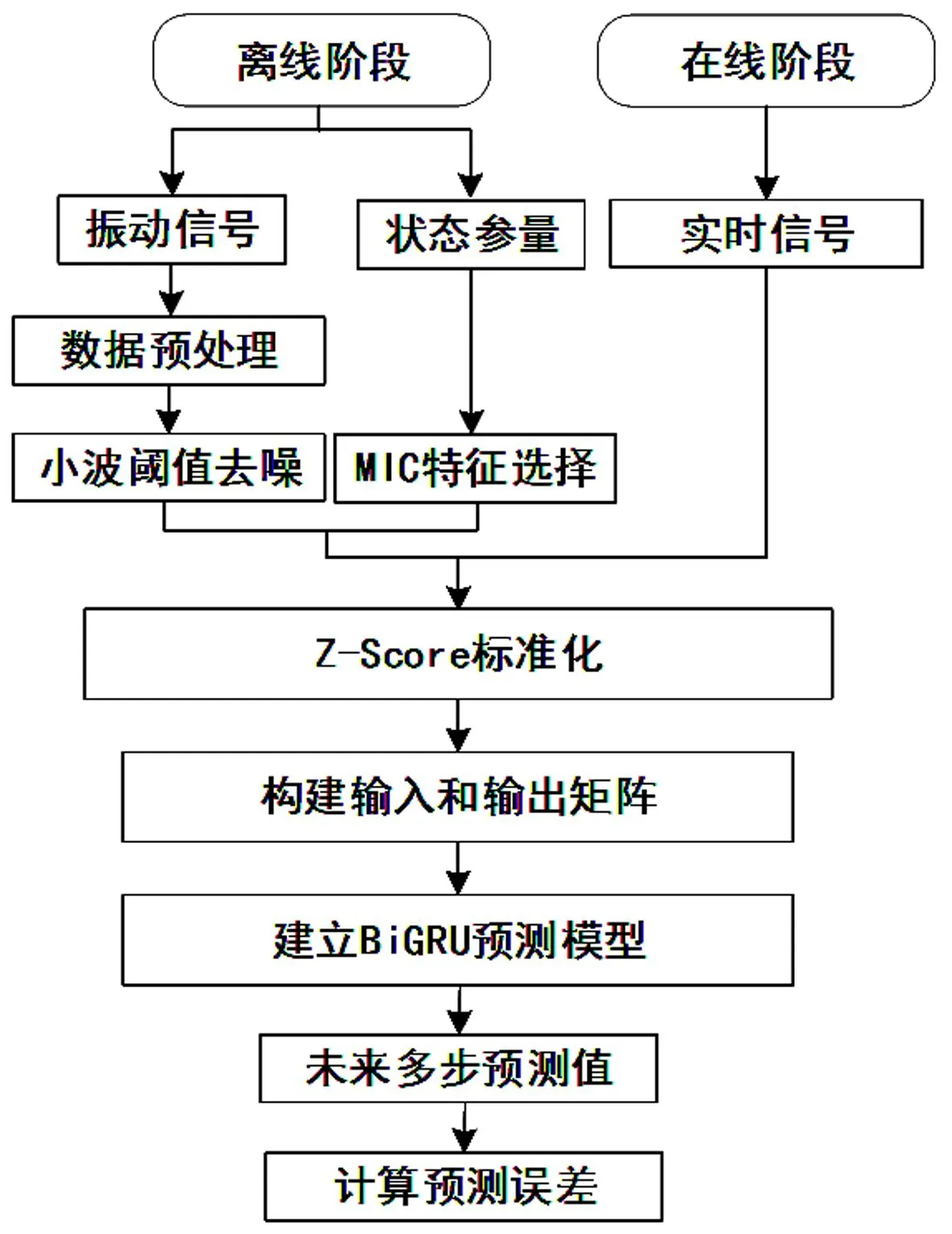
圖1 WTD-MIC-BiGRU 預測模型流程

（2）在線階段。步驟1，獲取實時狀態變量集、振動集；步驟2，對實時信號進行Z-score 標準化，并構建輸入矩陣；步驟3，將實時信號樣本矩陣輸入到訓練好的BiGRU 模型進行預測，獲取實時未來多步預測值；步驟4，計算真實振動值與預測值之間的誤差。

2.2 信號預處理水電機組振動信號去噪效果的優劣直接影響到預測的精度。為了減少噪聲對預測精度的影響，本文使用小波去噪對采集的原始振動信號進行去噪處理。小波分析是一種多尺度的時間頻率信號局部化分析的方法，可以自動適應時頻信號分析的要求，解決了Fourier 變換的困難問題［14］。常用的小波去噪方法分為小波系數閾值去噪法、小波變換模極大值去噪法以及小波分解與重構去噪法，其優缺點如表1所示。

水電機組在運行過程中采集的原始振動信號和噪聲的頻帶是無法確定的，且不需要考慮信號中的奇異點，因此本文選用小波系數閾值去噪法對振動信號進行降噪處理，其基本原理是將原始信號進行分解，并通過設置臨界閾值φ ，對分解后的各層系數進行處理。若小波系數小于φ ，則認為該系數主要由噪聲引起，需要去除這部分系數；若小波系數大于φ ，則認為該系數主要是由信號引起，需保留這部分系數，最后重構處理后的各層小波分量得到最終信號。小波閾值的設定［15］直接關系到去噪效果好壞，設的太高會使信號失真，太低會殘留噪聲。硬閾值不易產生偏差，重構信號的保真度高。本文運用極大極小閾值法確定閾值φ［16］，公式如下：

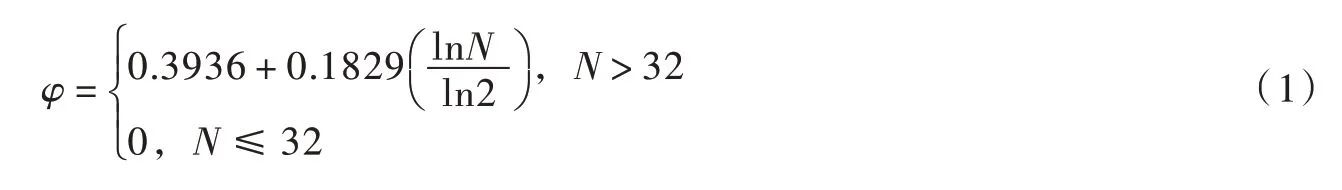
式中N 為小波系數個數。

表1 不同小波去噪方法優缺點對比

去噪系數可以作為衡量降噪效果的指標，其公式表示為：

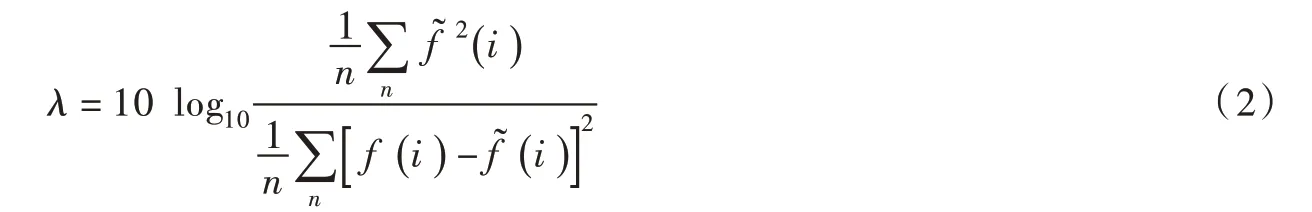
λ 值越小，降噪效果越好。

信號處理以后需縮小和統一樣本尺度以滿足對檢測速度和樣本數量的要求，本研究采用Z-Score算法對訓練數據進行標準化。其計算公式如下：

式中：x 為特征；x*為標準化后的數據；為均值；σ 為標準差。

由于水電機組處于頻繁的發電和抽水啟停過程中，信號采集數據不均勻，本研究根據采集間隔時間將數據樣本劃分為多個周期，一個周期即為一次開停機過程，并分別在發電工況和抽水工況下建立預測模型。

2.3 最大信息系數分析水電機組在運行過程中受多方面因素的影響，因此振動趨勢預測需要考慮其他變量的影響以更好擬合振動趨勢，減小模型復雜度。本文主要考慮了在抽水和發電工況下影響機組振動的內部和外部因素，利用MIC 計算各變量與振動信號間的非線性關聯性，最后選擇關聯性較大的變量作為參考輸入。相比于Pearson、Spearman 等線性相關性分析方法，MIC 具有較好的普適性和穩健性，能敏感挖掘兩個變量間的深度關聯性［17-18］。狀態變量xu與振動y 之間MIC 計算如下：

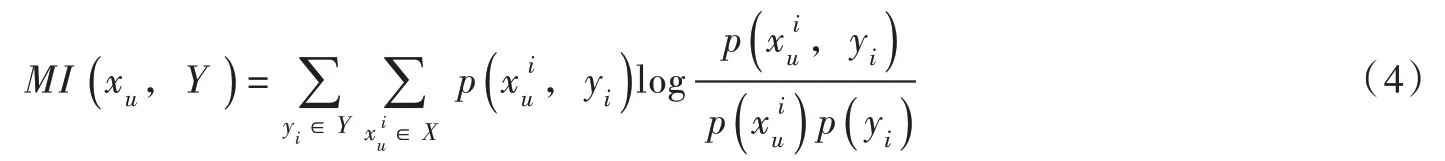
步驟2：將數據集D 中變量xu和Y 劃分到r、s 兩個格子中，并記為G=（r，s），為獲得使MI 最大的網格劃分，使用歸一化將MI 數值歸一化到（0，1）區間內進行比較，取不同方式中最大的MI 值為劃分G 下的MI 值，則歸一化后最大互信息可表示如下：

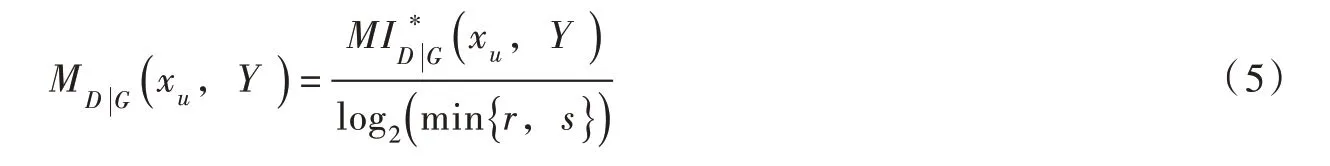
步驟3：選擇D 中最大的MI 值作為MIC 值。較高的MIC 值表明變量xu和Y 之間有很強的相關性，較低的MIC 值則表明較低的相關性，MIC 的計算公式如下：

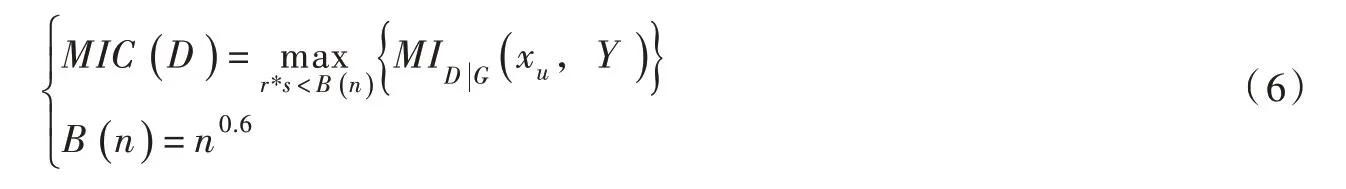
式中：MIC（D）為變量xu和Y 之間的MIC 值；B（n）為樣本大小n 的函數。

通過計算每個特征和狀態變量之間的MIC值來獲得最優特征集。如果不滿足公式（7）的特征將被刪除。

式中：xu為第u 個特征；Y 為振動信號；MICi為第u 個特征和振動信號Y 之間的MIC 值；σ為特征選擇閾值。

為挑選出在傳感器噪聲影響下，最能代表水電機組運行狀態的特征，水電機組振動信號與各狀態變量之間的MIC 值被計算，通過計算其平均值，可以反映出振動信號與各狀態變量間敏感性相關性的平均水平，與振動信號間MIC 值大于閾值的則被認為是有效特征［19］，其計算公式為：

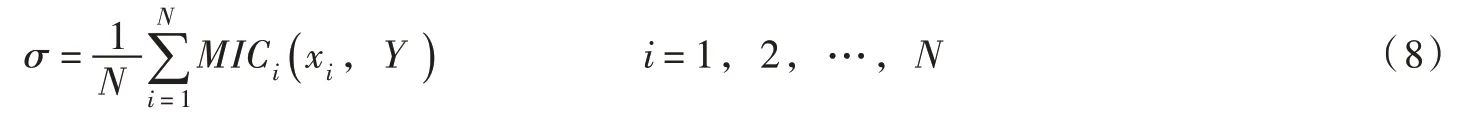
式中N 為狀態變量個數。

2.4 雙邊門控循環神經網絡BiGRU 模型［20］包括輸入層、前向傳播層、后向傳播層和輸出層4 個部分，分為前向傳播和后向傳播兩個過程。它通過向前和向后兩個GRU 對每一個時間序列進行訓練。BiGRU 網絡結構如圖2所示，輸入層對應于輸入時間序列的節點；前向傳播層為從左向右傳遞的GRU 網絡，其隱藏狀態為，后向傳播層為從右向左傳遞的GRU網絡，其隱藏狀態為，前向和后向傳播層的節點連接輸入層以及上一個輸入節點的輸出；輸出層則為前向和后向傳播層的隱藏狀態之和。t時刻隱藏狀態計算如下：

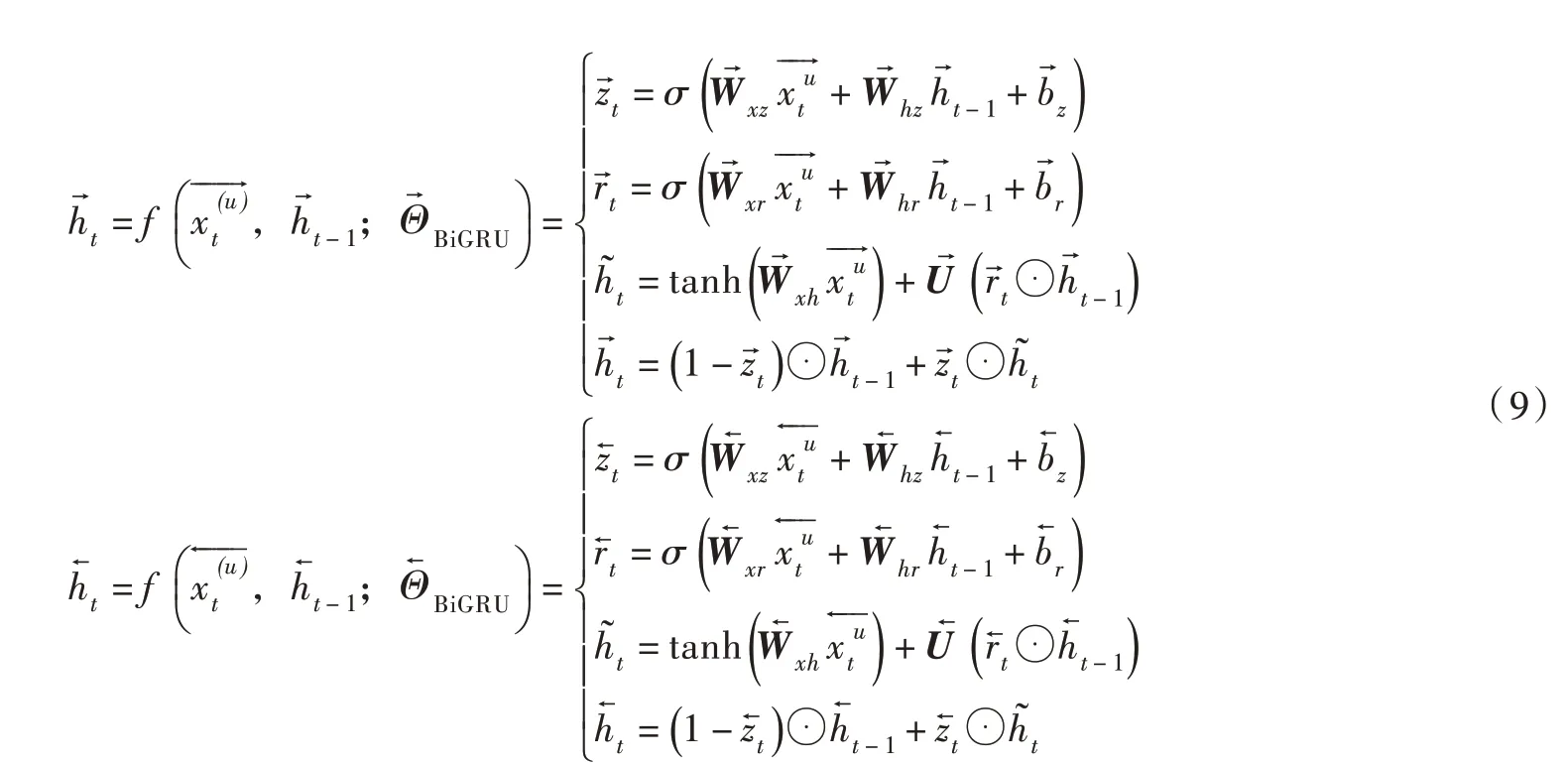
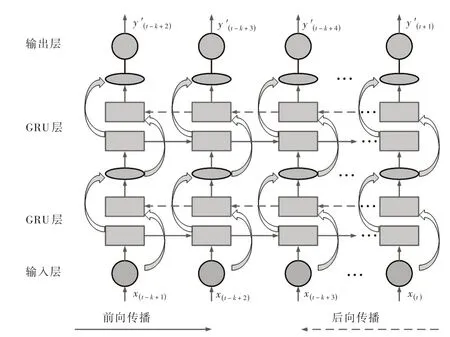
圖2 BiGRU 網絡結構

3 案例分析

3.1 數據獲取實驗數據取自浙江仙居抽水蓄能電站，其安裝了4 臺單機容量為375 MW 的混流可逆式水輪發電機組，單機容量為375 MW，水輪機額定水頭為447 m。水泵水輪機型式為立軸、單級、混流式，與額定轉速為375 r/min、50 Hz 發電電動機通過主軸法蘭直接連接。轉動方向為水輪機工況俯視順時針，水泵工況俯視逆時針。機組采用半傘式結構，兩根軸三導支撐，推力軸承支架在發電機下機架上。機組采用上拆方式，水泵水輪機可拆卸部件如轉輪、主軸、主軸密封、水導軸承、頂蓋、導葉、導葉操作機構、接力器、止漏環均可以利用廠房內的橋式起重機通過發電電動機定子內孔吊出和吊入。通過傳感器技術，獲取了機組各部件的實時信號數據，本文中運用其1 號機組水泵水輪機中水導軸承X 向擺度監測數據，信號采樣時間為1 min，選取2018年4月5日至10月5日的歷史振動數據進行訓練和測試，因機組處于頻繁的抽水和發電的啟停過程，可將數據進行周期化，刪除周期長度小于50 的樣本數據，則發電工況下，可得386 組周期數據樣本；抽水工況下，可得296 組周期數據樣本，取95%為訓練樣本，其余為測試樣本。圖3 截取展示了2018年6月2日至5日的水導軸承X 向擺度數據。

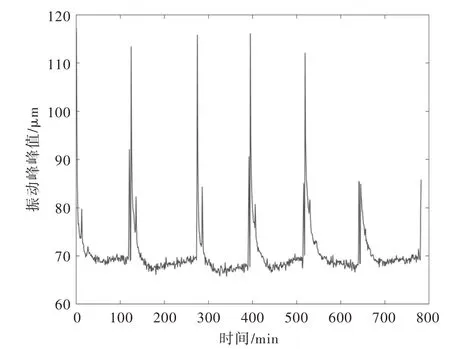
圖3 水導軸承X 向擺度監測數據

3.2 小波閾值去噪小波閾值去噪算法中小波基、分解層數對于信號去噪效果有很大的影響。合適的小波基會使得噪聲能較好在小波系數中體現，容易被濾除，去噪效果相對較好。分解層數決定了信號提取的純凈程度，層數太少會導致去噪效果不明顯，層數太多會導致信號失真。實際應用中最為廣泛的小波基有Symlets（Sym）和Daubechies（Db）兩種小波基。圖4 展示了抽水態下振動信號在不同小波基和分解層數下的去噪系數大小。根據分解結果可知，Db 基波在分解層數為5，Sym 基波在分解層數為6 時后系數變化小，且信號保真度高。就小波系數而言，Db9、Db10、Sym6、Sym7、Sym8 去噪效果最好。

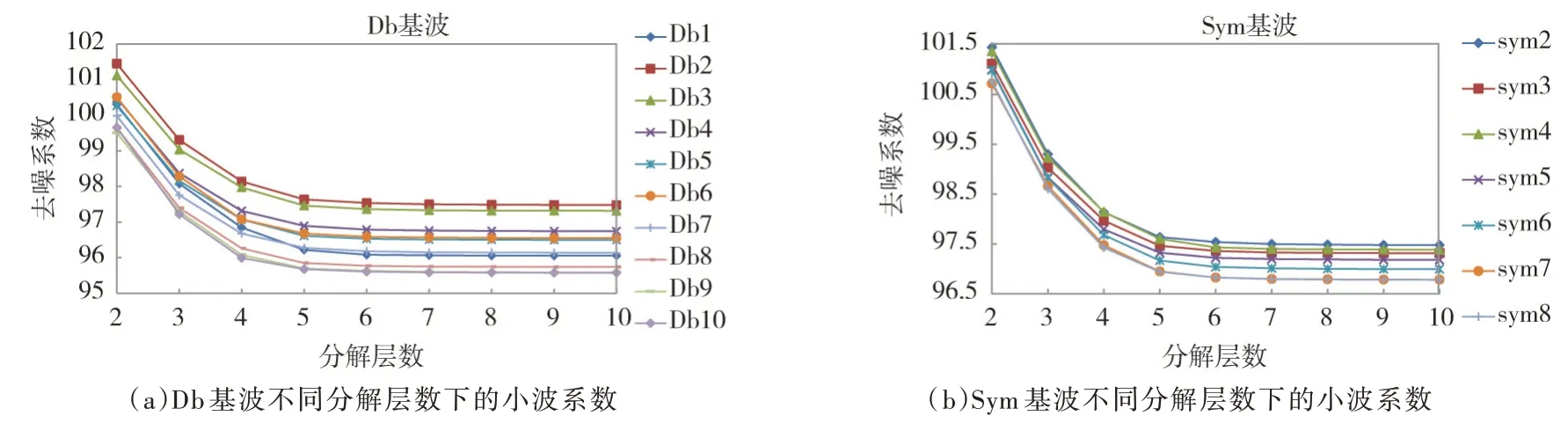
圖4 水導軸承X 向擺度在Db 和Sym 基波下不同分解層數的去噪系數對比

表2 展示了不同基波的誤差指標RMSE 以及去噪系數λ的結果，選用小波基Db 時，小波系數最低，且RMSE 較小，因此本文中小波閾值去噪最優參數選擇為基波Db10，分解層數選擇5。圖5 展示了抽水態下某周期水導軸承X 向擺度信號去噪前后對比結果，去噪后的振動信號保留了突變點等信息，但很好的濾除了噪音。

表2 不同基波下去噪誤差效果對比

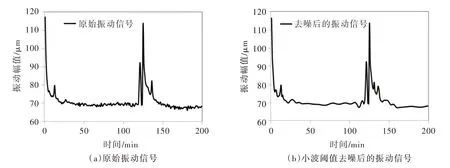
圖5 水導軸承X 向擺度去噪前后效果

3.3 特征相關性分析在實際工程應用中，水電機組振動由水力、電氣與機械不平衡力驅動，機組的異常振動多為電氣、機械與水力振動耦合而成，因此在建立振動趨勢預測模型時，需考慮不同工況下狀態參數的影響，本文首先基于人工經驗分析影響水導軸承X 向擺度V 的狀態變量有：水頭H、有功功率P、上導油槽油溫T、勵磁電流I、勵磁電壓U、軸向位移D、機組轉速S、導葉與轉輪進口間壓力脈動V1與轉輪與頂蓋間壓力脈動V2，采用MIC 分析狀態變量與水導軸承X 向擺度之間的相關性，選取出相關性較強的變量與振動信號作為模型輸入，各狀態變量與振動信號之間的MIC 值如圖6所示，水平坐標為特征標簽，縱坐標為各變量與振動信號間的MIC 值，通過式（8），最終的閾值計算為0.6。根據結果可知，有功功率、水導油槽油溫、軸向位移以及導葉與轉輪進口間壓力脈動與水導軸承X 向擺度的關聯性最強，因此本文輸入為有功功率P、水導油槽油溫T、軸向位移D、導葉與轉輪進口間壓力脈動V1和水導軸承X 向擺度V。

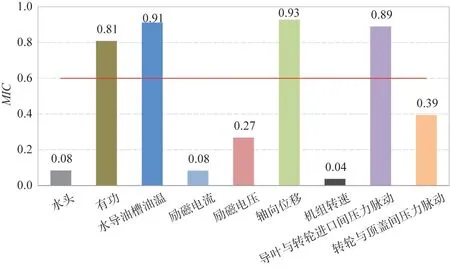
圖6 狀態變量與振動信號間的MIC 值

3.4 預測結果本文提出了基于WTD 的信號去噪、基于MIC 的特征選擇、基于BiGRU 網絡的混合預測模型WTD-MIC-BiGRU，為驗證各部分及整體方法的有效性，將所提方法與BiGRU、MIC-BiG?RU、WTD-BiGRU 模型比較，證明數據處理、信號去噪、特征選擇的必要性和有效性；通過與WTD-Pearson-BiGRU 模型比較，突出MIC 挖掘深層非線性關系的優點，而Pearson 相關系數僅考慮了變量間的線性關系；通過與WTD-MIC-LSTM、WTD-MIC-GRU 模型比較，顯示了本文所提出的BiG?RU 網絡處理和學習多變的非線性時間序列數據的優越性。在對比實驗中，BiGRU、WTD-BiGRU 模型中未考慮狀態變量影響，模型輸入為單變量水導軸承X 向擺度，表3 展示了7 種模型的參數設置。本文的訓練及測試均在在Python 的Pytorch 平臺上建立深度神經網絡，運行Windows10 的計算機上采用2.33GHz Intel Xeon?CPU，RAM 16 GB 的微機平臺。

表3 不同模型的參數設置對比

7 種預測模型在發電工況和抽水工況下的多周期平均預測誤差如表4所示，本文采用均方根誤差（Root mean squared error，RMSE）和平均絕對誤差（Mean absolute error，MAE）兩種評價指標對模型預測結果進行定量分析［21］，依據表4 中結果，可從三方面分析模型效果。

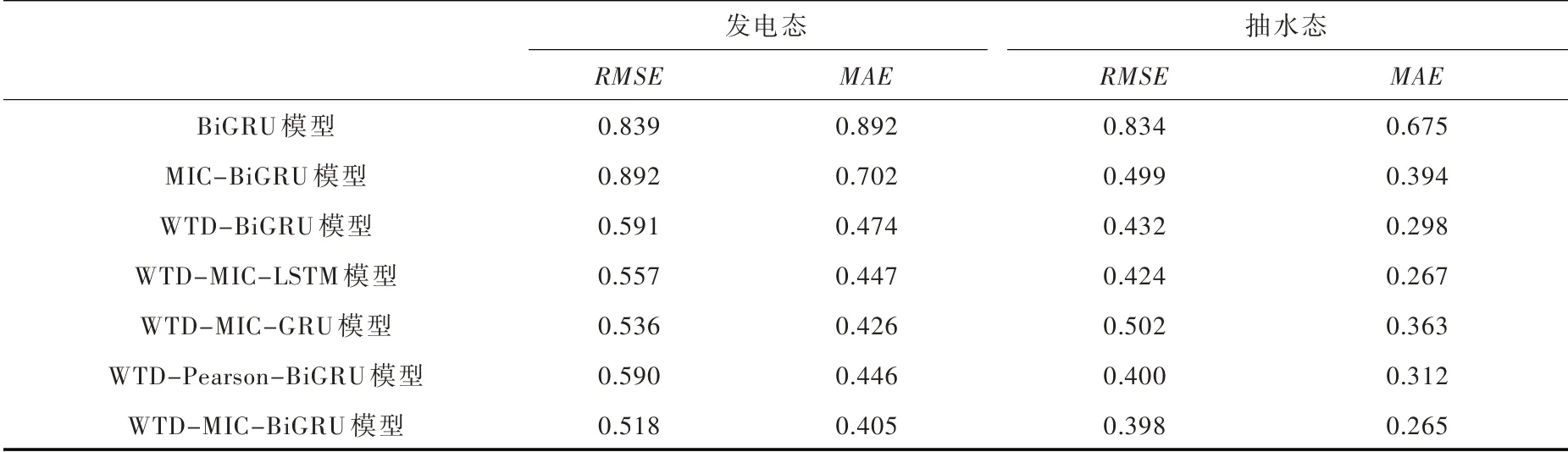
表4 不同模型的預測結果對比

（1）信號去噪。對比MIC-BiGRU 模型與所提WTD-MIC-BiGRU 模型預測結果可以看出，當使用小波閾值去噪后，水電機組振動趨勢預測精度有大幅度地提升，發電態和抽水態下預測精度分別提升0.487RMSE、0.297MAE 和0.101RMSE、0.129MAE，這表明小波閾值去噪可以有效提出噪音，保留原始振動信號的特性，從而進一步提高預測精度。

（2）特征選擇。當不考慮相關參考輸入時，即WTD-BiGRU 模型，預測誤差相比WTD-MIC-BiG?RU 模型有所減小，但仍具有一定差距。而水電機組在運行過程中需要考慮狀態變量對模型的影響，選擇合適的狀態變量可以提高預測模型的穩定性和精確度，避免單變量異常值的影響。對比WTD-Bi?GRU 模型與WTD-Pearson-BiGRU、WTD-MIC-BiGRU 模型預測結果可知，進行特征選擇后，預測結果均有一定改善；由于Pearson 方法挖掘的是變量間的線性關系，而MIC 對于變量之間的非線性關系更敏感，更能準確反映出變量間的聯系，基于MIC 選擇出的變量作為參考輸入，預測效果更好。

（3）深度預測模型。當采用相同信號處理WTD 與特征選擇MIC 時，LSTM 網絡獨特的循環結構使之對時間序列數據的學習與預測能力更強，也表現出較低的預測誤差，而GRU 網絡由于其更加優化的結構使得模型的泛化能力更強，預測誤差在RMSE 和MAE 指標中相比LSTM 減小。而BiGRU 網絡同時學習未來和歷史信息，使得預測更加準確。

為進一步直觀展示不同模型的預測結果，圖7 展示了WTD-BiGRU、WTD-Pearson-BiGRU、WTD-MIC-GRU、WTD-MIC-BiGRU 等4 種典型模型在發電工況和抽水工況下某一個隨機周期的測試結果，與原始振動數據以及經過WTD 去噪后的數據對比結果。從圖中可以看出，在發電態工況下，由于開機時受其他部件的影響，機組的振動幅值較大，因此在開機附近呈現出一定的誤差，但在使用小波系數閾值去噪后，整體預測效果具有一定的穩定性；在抽水態工況下，振動數據較為平穩，所提方法預測更加準確。綜上所述，本文所提出的WTD-MIC-BiGRU 模型的預測效果表現出更好的精準性和穩定性，能為機組設備異常預警提供有效支持。

圖7 不同模型預測結果對比

4 結論

為準確預測水電機組未來振動趨勢，本文針對高頻振動信號噪聲大的問題，對信號進行小波閾值去噪，以濾除噪聲；其次，考慮到水電站設備運行中多方面因素的影響，提出基于最大信息系數的特征選擇方法，通過挖掘變量間非線性關系以挑選出與振動信號最相關的工況參數；最后，提出基于雙邊門控循環神經網絡的趨勢預測方法，有效提升模型的預測精度和泛化性能。通過工程實例數據對所提方法體系中各部分的驗證和現有流行方法的對比，實驗結果表明，本文所提出的數據處理方法WTD-MIC，結構參數少，具有較高的自適應性，充分挖掘狀態監測數據中的特征，避免了人工經驗的依賴和不足；另外基于深度學習的雙邊門控循環神經網絡也具有一定的優越性，在預測精度和泛化性能上均能夠滿足工業要求。

本文結論具體如下：（1）基于小波系數閾值去噪的方法保留了水電機組振動信號的原始特性，在去除噪聲的同時，很好的保留了局部尖峰振動信號，避免局部峰值振動信號的失真，有效為故障預警提供實時方案；（2）基于最大信息系數的特征選擇方法，充分考慮了相關變量與振動信號間的非線性關聯性，避免了人工經驗的不足以及單變量預測帶來的不穩定；（3）基于雙邊門控循環神經網絡的時序預測方法，充分利用歷史和未來時刻的信息，有效提取真實振動信號變化特征，建立了強泛化的映射關系，提高了預測精度；（4）通過工程數據實驗表明，本文所提出的WTD-MIC-BiGRU 模型中，小波系數閾值去噪、最大信息系數以及雙邊門控循環神經網絡相比已有研究中常用的去噪方法、特征選擇方法以及深層模型具有更好的效果，可在實際工程應用中為機組狀態檢修提供一定參考。