基于改進自回歸流模型的壩基三維裂隙網絡多參數模擬

張亦弛，呂明明，關 濤，王佳俊，余 佳，任炳昱

（天津大學 水利工程仿真與安全國家重點實驗室，天津 300072）

1 研究背景

對于水電工程壩基裂隙巖體，探明其內部的裂隙發育情況能夠為壩基工程地質分析與決策提供關鍵依據，對于保障水電工程的安全穩定具有重要的理論與現實意義［1-3］。裂隙是指巖石受到構造變形的破裂作用或物理成巖作用形成的沒有明顯位移的面狀不連續體［4］，在巖體內部常呈現網狀分布。離散裂隙網絡（Discrete Fracture Networks，DFN）模型是由Baecher 等［5］提出的一種研究裂隙空間展布的有效手段，該方法將每一個裂隙表達為一個具有厚度的圓盤模型。基于從巖體表面露頭與內部鉆孔中觀測的裂隙先驗信息，通過示性點過程進行裂隙網絡隨機建模，其中點過程基于穩態泊松過程確定裂隙中心點的位置［6］，示性過程確定裂隙的屬性，即圓盤裂隙的幾何參數［4］。

三維離散裂隙網絡模型本質上是對巖體內裂隙的傾向、傾角、直徑、開度等屬性特征聯合分布的幾何表達［4，6］，因此，裂隙網絡的多參數模擬是目前的研究趨勢［6-8］，其關鍵問題在于對裂隙的幾何參數之間的多維聯合分布進行概率密度估計與采樣。現有的DFN 建模方法通常假設裂隙的幾何參數之間互相獨立，并采用典型分布對每個參數的邊緣分布進行概率密度估計（Probability Density Estima?tion）與采樣（Sampling），例如：描述直徑與跡長的Gamma 分布與對數正態分布、描述開度的負指數分布與對數正態分布、描述走向的Von-Mises 分布等［4，6，9］。Mendoza-Torres 等［10］的研究指出現有DFN建模研究通常采用的單參數模擬方法忽略了裂隙幾何參數之間可能存在的相關性［10］，當實測裂隙參數之間不獨立時，分別從各邊緣分布中抽樣的結果不一定會服從聯合分布，相反，直接對聯合分布進行估計的方法自然地考慮了參數之間的相關性［10］。然而，傳統的DFN 建模方法僅針對傾向與傾角參數考慮了聯合分布估計的問題，且仍然采用典型分布假設，包括：Fisher 分布、雙正態分布、Bing?ham 分布、Kent 分布等［6，11］。事實上，由于巖體內部裂隙發育的內在規律十分復雜，工程實測數據中三個以上裂隙幾何參數的聯合分布一般不符合上述幾種典型分布中的任何一種［10］，此時基于典型分布的估計方法缺乏足夠的擬合能力［10］，且嚴格的分布類型假設可能帶來偏倚與誤差［10-11］。綜上，目前的DFN 建模方法面臨著難以有效擬合多維幾何參數的聯合分布的難題，亟待提出一種能夠靈活且準確地對實測裂隙的多參數聯合分布進行概率密度估計與采樣的方法，從而實現DFN 的多參數模擬。

深度生成模型屬于一種深度學習模型［12-13］，其優勢在于能夠學習分布類型未知的高維聯合分布并從中采集高質量的樣本，能夠克服傳統統計學模型難以擴展到高維問題的不足［14-15］，對于突破DFN多參數模擬的瓶頸具有較大的潛力。深度生成模型近幾年開始被應用于建立更加真實的大尺度地質構造三維模型［16］，但尚未被引入DFN 建模的研究中［17-18］。

2017年，Papamakarios 等［19］與Kingma 等［20］提出了一種新的深度生成模型——自回歸流（Autore?gressive Flow），該模型通過建立易解的概率密度（Tractable Density）實現對于復雜分布下對數似然函數值的精確計算［21］，克服了其他基于變分推斷（Variational Inference）的深度生成模型需要對概率密度進行近似估計的不足［12］，具備能夠實現更加準確的概率密度極大似然估計的優勢［14-15］，因而成為了目前深度生成模型領域的研究熱點，應用于概率密度估計［19］、變分推斷［20］、圖像生成［22］、語音合成［23］、文本生成［24］等方向的研究。本文將自回歸流模型引入DFN 建模中。裂隙網絡的幾何參數通常具備優勢分組的現象，即巖體在多次構造作用下產生的裂隙網絡的幾何參數聚集于幾個峰值附近［6，8］，導致其幾何參數的分布呈現出多峰的特點。然而，自回歸流模型的初始分布通常采用一個單峰的高斯分布，對于多峰分布的估計能力有待提高。因此，本文提出基于改進自回歸流模型的裂隙多參數模擬方法，將自回歸流模型的標準化特征空間的高斯分布改進為高斯混合分布并結合DensityPeak 聚類算法［25］提出了密度峰值聚類自回歸流（Density Peak Clustering Autoregressive Flow，DPCAF）模型。其中，密度峰值聚類（Density Peak Clustering）算法于2014年發表于Science［25］，是目前最受關注的聚類算法之一，具有能夠從任意維度任意形狀的數據中快速確定簇的數量與聚類中心的優勢［26］，適用于裂隙幾何參數的聚類問題。本文提出DPCAF 模型以期能夠有效擬合裂隙幾何參數的多維多峰聯合分布，有效提高裂隙網絡多參數模擬的精度，并使得DFN 模型更加真實地反映巖體內部的裂隙分布。

2 研究框架

提出的基于密度峰值聚類自回歸流（Density Peak Clustering Autoregressive Flow，DPCAF）模型的三維裂隙網絡建模方法的研究框架如圖1所示，具體如下：

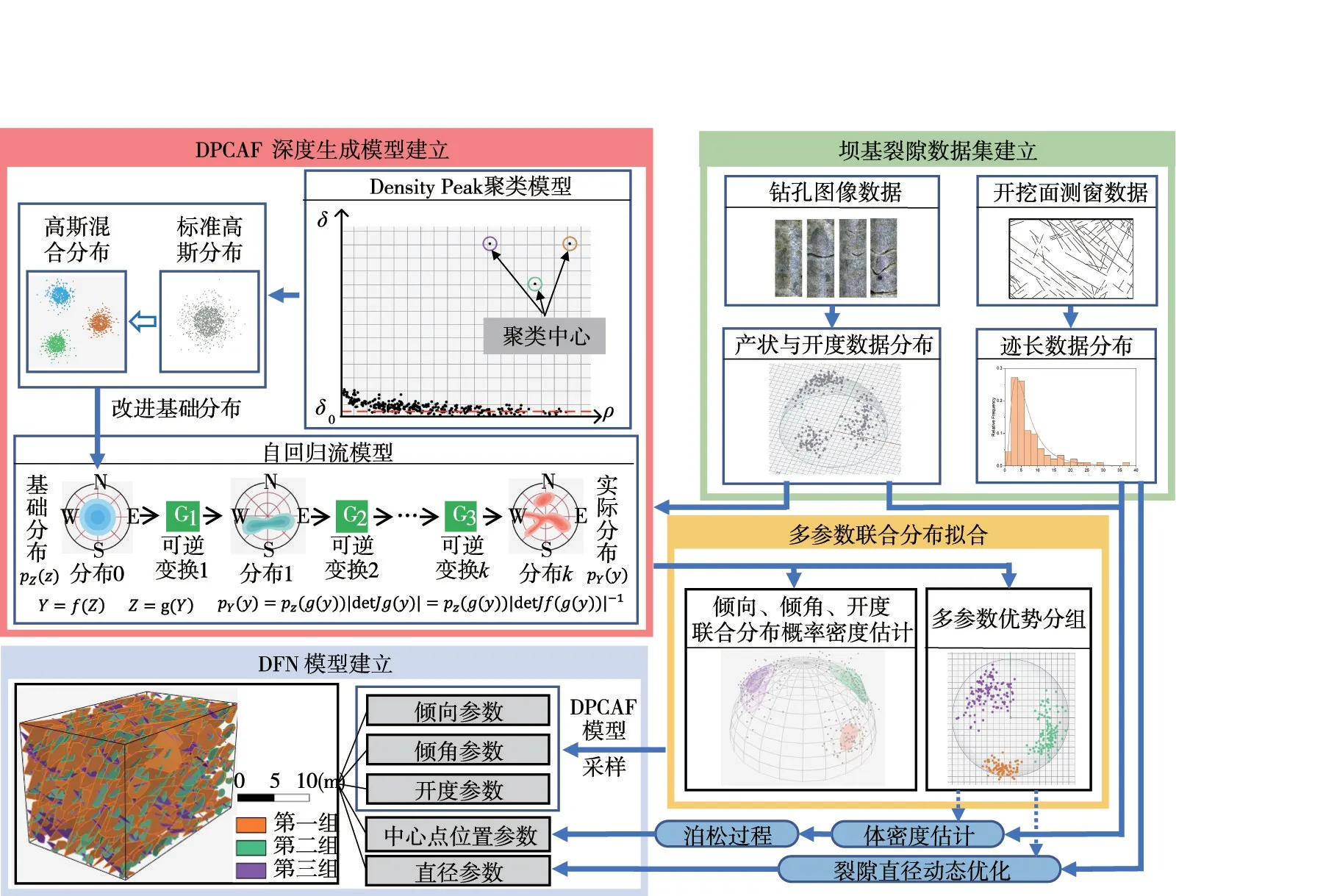
圖1 研究框架

（1）建立壩基裂隙數據集。從壩基裂隙巖體的鉆孔圖像數據中提取出巖體內部裂隙的傾向、傾角、開度三個維度的幾何信息［6，27-28］，由于鉆孔圖像中未包含裂隙直徑信息，從建基面測窗數據中統計裂隙跡長的分布，用于輔助推斷裂隙直徑參數；

（2）建立DPCAF 深度生成模型。將自回歸流模型標準化特征空間的基礎分布由標準高斯分布改進為高斯混合分布，并結合DensityPeak 聚類算法確定裂隙分組數量與聚類中心，建立改進的自回歸流模型DPCAF，利用產狀與開度的實測數據集訓練DPCAF 模型參數；

（3）多參數聯合分布擬合。利用訓練完成的DPCAF 模型對傾向、傾角、開度參數的聯合分布進行概率密度估計，同時實現多參數優勢分組；

（4）DFN 模型建立。基于裂隙多參數優勢分組結果，聯合測窗數據與鉆孔圖像數據對每組裂隙的體密度（單位體積內的裂隙數量）進行估計，并通過泊松過程得到各組裂隙中每一個裂隙面的中心點坐標參數；利用DPCAF 模型對傾向、傾角、開度參數隨機采樣；基于測窗數據中的裂隙跡長分布優化裂隙直徑參數；最后，基于圓盤裂隙模型，建立三維離散裂隙網絡。

3 基于密度峰值聚類自回歸流的DFN 多參數模擬方法

3.1 密度峰值聚類自回歸流模型由于裂隙網絡的幾何參數普遍存在優勢分組的現象，其分布呈現出多峰的特點。然而，自回歸流模型的初始分布采用一個單峰的高斯分布，估計多峰的概率密度的能力有待提高。針對以上不足，本文提出的DPCAF 模型，將自回歸流模型的標準化空間的高斯分布改進為一個由均值、方差和各分支的混合比例所參數化的高斯混合分布，并結合DensityPeak 算法，以無監督的形式實現裂隙多參數優勢分組與多參數聯合概率密度估計的多任務學習，提高對實測裂隙數據多峰分布的擬合精度。

自回歸流模型屬于一種標準化流（Normalizing Flow）［14-15］，如圖2所示，其核心思想是將一系列簡單的可逆變換函數作為組件以“流”的形式依次嵌套為一個可逆的復合函數，構造出一個具有更強擬合能力的非線性雙射，通過在實際數據的目標分布與已知的基礎分布之間互相轉換實現多維聯合分布的估計。

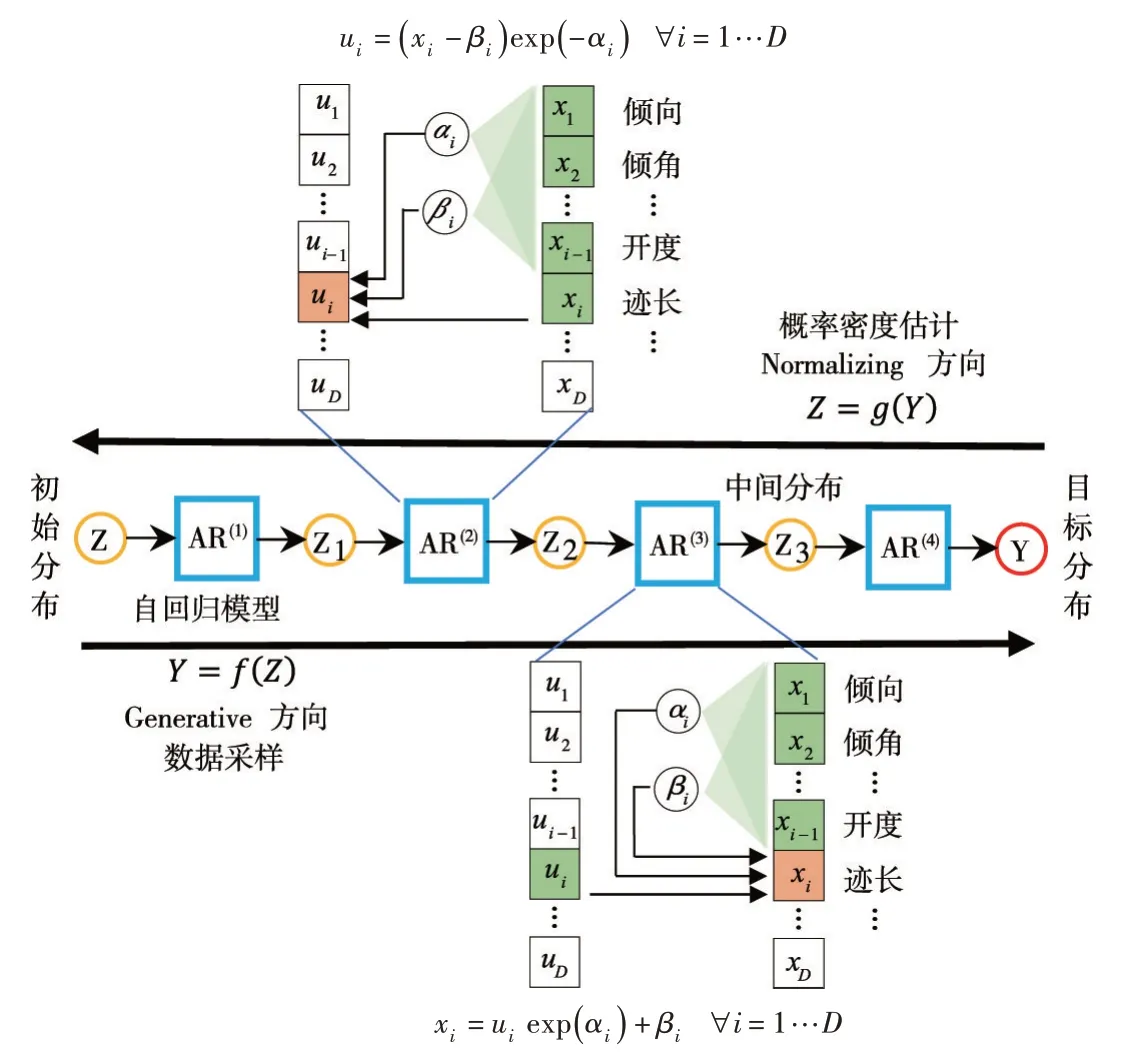
圖2 自回歸流模型網絡結構［19］

令隨機變量Z ∈RD服從已知的基礎分布，隨機變量服從目標分布。利用N 個雙射函數 f1，f2，…，fN的復合函數f 構建可逆變換，將基礎分布變換為一個未知的目標分布，即，其逆變換為雙射函數 g1，g2，…，gN的復合函數g，即。 根據Change-of-Variables 公式［14］，令J 為雅克比行列式算子，則目標分布的概率密度函數如下：

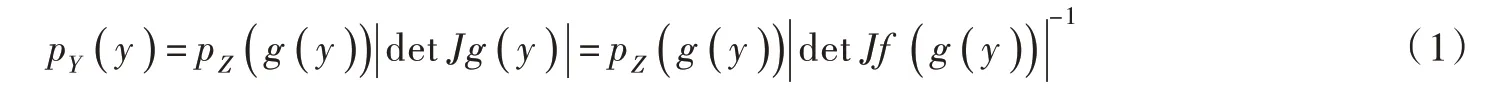
變換f 的方向稱作生成方向（Generative Direction），是進行采樣時的數據流向，逆變換g 的方向稱作標準化方向（Normalizing Direction），通常將復雜不規則的目標分布變換為多元標準高斯分布［19-20］，是評估模型概率密度值的數據流向，如圖2所示。為了保證模型訓練和預測的計算效率，要求可逆變換f 具有易解的雅克比行列式（Tractable Jacobian Determinant）。因此，引入另一種深度生成模型——自回歸模型（Auto-Regressive Model，AR）［29］，該模型基于概率鏈式法則將聯合概率密度分解為每一個維數上的條件概率的乘積［29］，并逐個對每一維數據的條件概率分布進行“自回歸”計算。以自回歸模型作為雙射函數 fi的標準化流模型稱作自回歸流模型（Autoregressive Flow）［19-20］，其中雙射函數 fi具有如下的自回歸形式：

式中：τ稱作變換函數（transformer）［14］；ci稱作第i 個調節函數（conditioner）；。

該公式的自回歸特性體現在：第i 個調節函數ci只能以第1 個至第i-1 個維度的變量z1:i-1為輸入，其雅克比矩陣為下三角陣。將公式（2）作為Normalizing 方向的逆變換g［19］，并選擇仿射變換形式的變換函數τ［14］，如下：

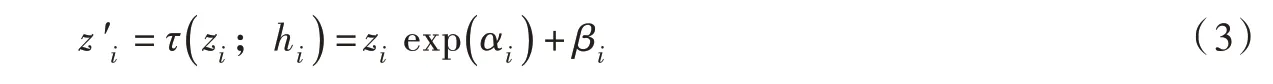
式（3）中的變換函數τ是可逆的，且形式簡潔且引入的參數量較少，在實測裂隙數據的小樣本數據集上不易過擬合［19-20］，同時對于裂隙數據具備足夠的擬合能力。此時雅克比行列式的絕對值為：

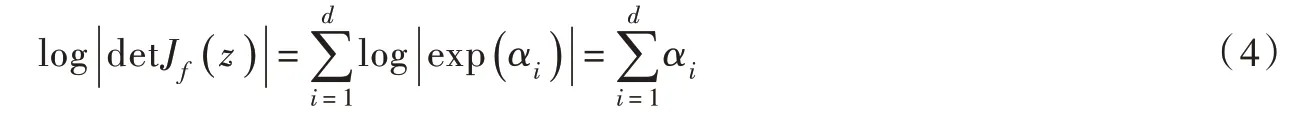
用掩模自編碼器（Masked AutoEncoder for Density Estimation，MADE）［29］構建調節函數ci，對多參數之間的相關性進行建模，逐個計算每個參數的條件概率并依據鏈式法則求得聯合概率密度。在訓練自回歸流模型的過程中，直接將負對數似然函數作為損失函數，通過梯度下降對每一個雙射函數 fi內部的仿射變換參數與掩模自編碼器參數進行優化。

本文提出的DPCAF 模型中，基于高斯混合分布與密度峰值聚類改進自回歸流模型的方法如下：

首先，建立混合高斯分布作為DPCAF 模型的基礎分布。高斯混合分布是一種混合分布，記作：

式中：Gi為混合分支，服從高斯分布；為支密度；為混合比例。

利用DensityPeak 算法搜索密度峰值點作為聚類中心，將簇的數量作為高斯混合分布中分量的數量，定義DPCAF 模型的基礎分布，其中每一個分量對應裂隙網絡的一個優勢分組。將深度生成模型的先驗分布由單峰分布改進為混合分布是提高模型對于多峰分布擬合能力的有效手段［30-32］。以赤平極射投影圖上的裂隙產狀數據為例，對比自回歸流模型與DPCAF 模型的基礎分布，如圖3所示。

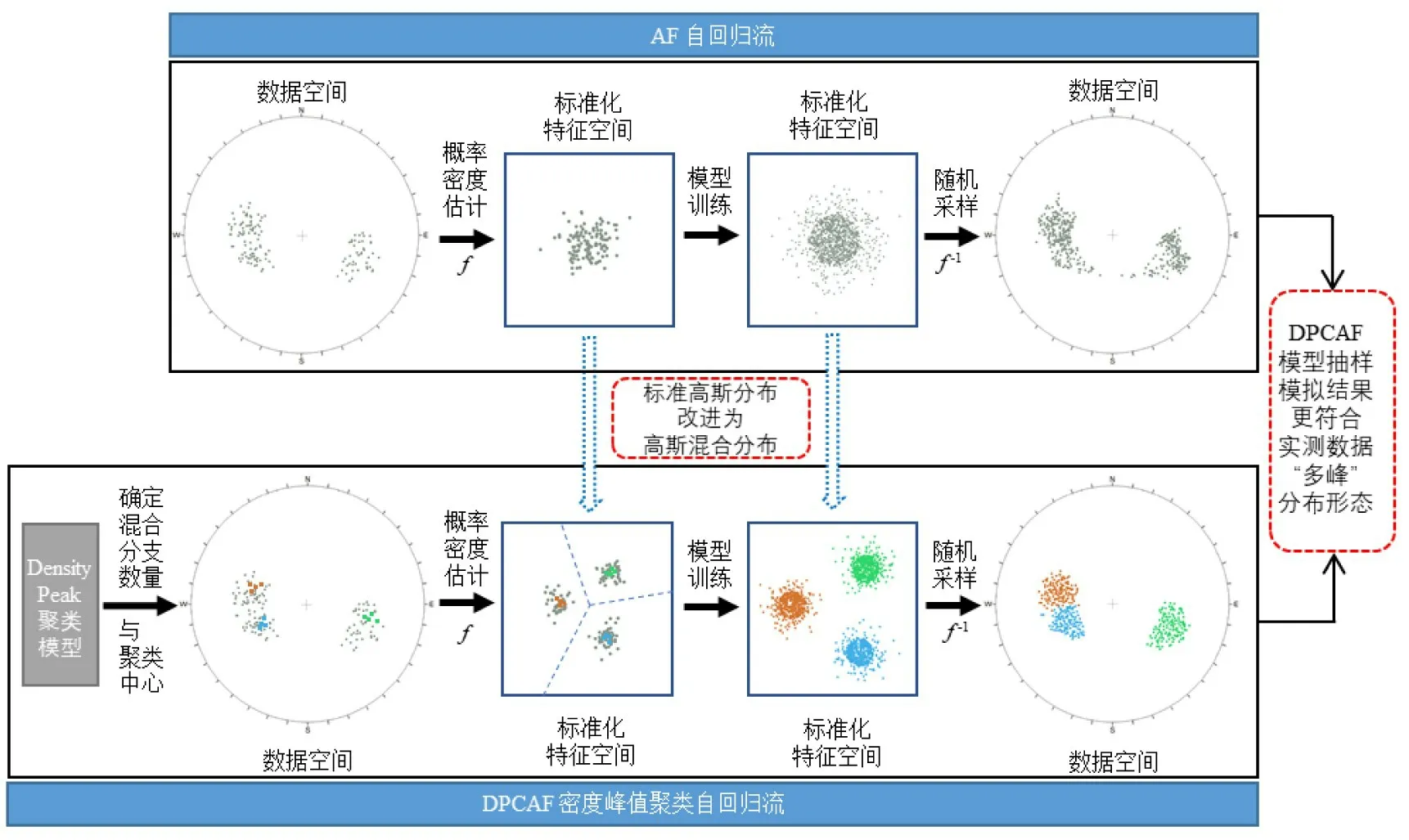
圖3 DPCAF 模型改進自回歸流模型示意

DensityPeak 算法所定義的密度峰值點包含兩方面特征［25］：（1）該點的局部密度大于其鄰近數據點；（2）該點與比它密度更高的數據點之間的距離較遠。

式中：ρi為局部密度，1/mm3；dc為截斷距離，mm；dij為數據點i 至數據點j 的距離，mm。當a<0時當a ≥0 時。

式中δi為與密度更高點的距離，mm。

其次，在以局部密度ρi為橫坐標，以距離δi為縱坐標，繪制出DensityPeak 決策圖上，自動提取出聚類中心附近的少量樣本點，作為已知分組標簽的訓練數據。搜索標簽數據的規則如下：（1）樣本點按照其在決策圖上的局部密度從大到小的順序篩選；（2）樣本點與具有更高密度的最近點的距離大于設定的δ0距離閾值，mm。

最后，利用分布擬合空間的實測數據與DensityPeak 算法提取的部分數據標簽訓練DPCAF 模型。將自回歸流的基礎分布定義為：

式中：高斯混合分布的混合分支數量為M，其中第k 個是均值為μk標準差為σk的高斯分布。

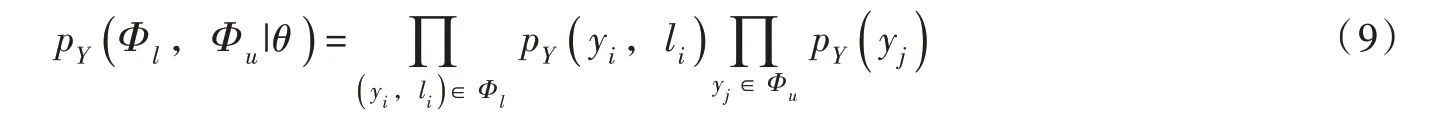
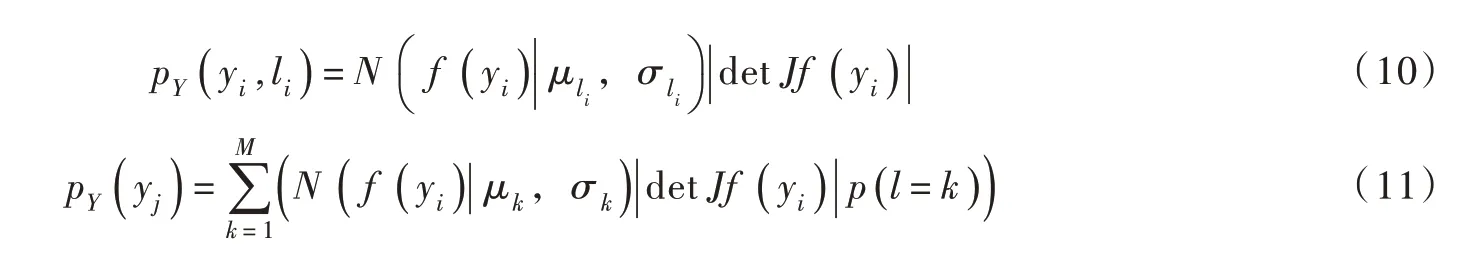
在最大似然估計的過程中對式（9）中的聯合似然函數進行最大化。根據貝葉斯定理，利用上述概率密度估計的結果計算出已知樣本點x 條件下標簽l 的條件分布，并訓練貝葉斯分類器實現裂隙分組。

3.2 基于DPCAF 模型的壩基巖體裂隙網絡多參數模擬流程為了更好地揭示鉆孔圖像數據中傾角、傾向、開度三個裂隙幾何參數的分布，本文建立了一個可逆的球坐標系轉換，將實測數據點映射到分布擬合空間的點，如圖4所示。其中：α 為裂隙面傾向，（°）；β 為裂隙面傾角，（°）；δ 為裂隙開度，又稱作隙寬，mm；x，y，z 為分布擬合空間中的直角坐標系下的坐標。其中對于裂隙開度這一維度，本文使用數據點到球坐標中心點的徑向距離對其進行表征，建立球面半徑與開度的轉換關系為，單位統一采用mm，其中δ0為開度的平均水平，實際工程的裂隙開度一般位于毫米至厘米量級，因此取δ0為10 mm，R0是開度等于δ0時的球面半徑，其數值也取為10 mm，λ 為縮放系數，本文取為0.1。

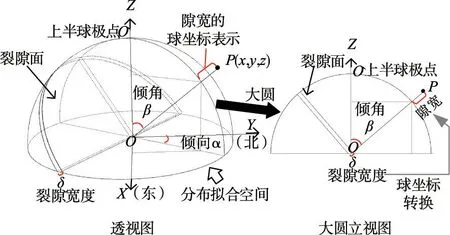
圖4 裂隙傾向、傾角、開度參數的球坐標系轉換過程

DFN 多參數模擬的具體步驟如下：

（1）將傾角、傾向、開度的原始實測數據通過上述球坐標系轉換為分布擬合空間的數據，并對DPCAF 模型進行訓練，將DPCAF 模型輸出的分布擬合空間每個數據點的標簽映射回原始數據，得到三個參數的優勢分組結果；

（2）DPCAF 模型輸出分布擬合空間的聯合概率密度函數，對從中采集的樣本進行球坐標系轉換的逆變換，從而得到傾角、傾向、開度參數的隨機模擬結果；

（3）基于裂隙網絡參數化建模計算模擬跡長分布下實測跡長數據平均對數似然，以裂隙直徑Gam?ma 分布的形狀參數和逆尺度參數為控制變量，以最大化似然函數為優化目標，利用粒子群優化（Par?ticle Swarm Optimization，PSO）算法［33］進行求解，從而得到直徑參數的隨機模擬結果。

4 工程實例

以我國西南某水電工程的壩基巖體為研究對象，基于所提出的基于DPCAF 模型的DFN 多參數模擬方法，針對河床高程范圍內的建基面下方50m×30m×30m（長×寬×深）區域范圍內的裂隙網絡進行三維建模。鉆孔圖像數據包含309 條實測裂隙，開挖面測窗數據包含231 條實測裂隙，如圖5所示。

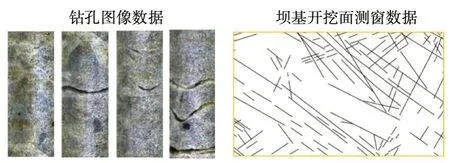
圖5 壩基巖體裂隙數據

4.1 基于DPCAF 模型的壩基DFN 多參數模擬從鉆孔圖像中提取的傾向、傾角與開度實測數據通過球坐標系轉換至分布擬合空間的結果如圖6所示，圖中黑色的點代表轉換后得到的數據，半透明的半球面是開度等于10 mm 的等參面。

首先，利用DensityPeak 聚類算法確定聚類的分組數量，以及每一組的聚類中心。可以明顯地發現DensityPeak 決策圖的右上角出現三個聚類中心點，而其余點均分布于靠近橫軸的區域，因此優勢分組數量為3 組。將決策圖中的點映射回三維坐標系內可以定位三個聚類中心的位置，如圖6所示。在DensityPeak 決策圖上自動搜索聚類中心附近的標簽數據，設定標簽數據在決策圖中縱坐標的閾值為圖6 中的紅色虛線，最終得到的每一組的標簽數據為20 個。

圖6 DensityPeak 算法搜索聚類中心

其次，利用所有實測數據點以及DensityPeak算法自動搜索得到的標簽信息對DPCAF 模型進行訓練。圖7 對訓練完成的DPCAF 模型從分布擬合空間的數據中學習的三維聯合概率密度的形狀進行了可視化，其中對于每組裂隙繪制了兩個半透明的等概率密度曲面。

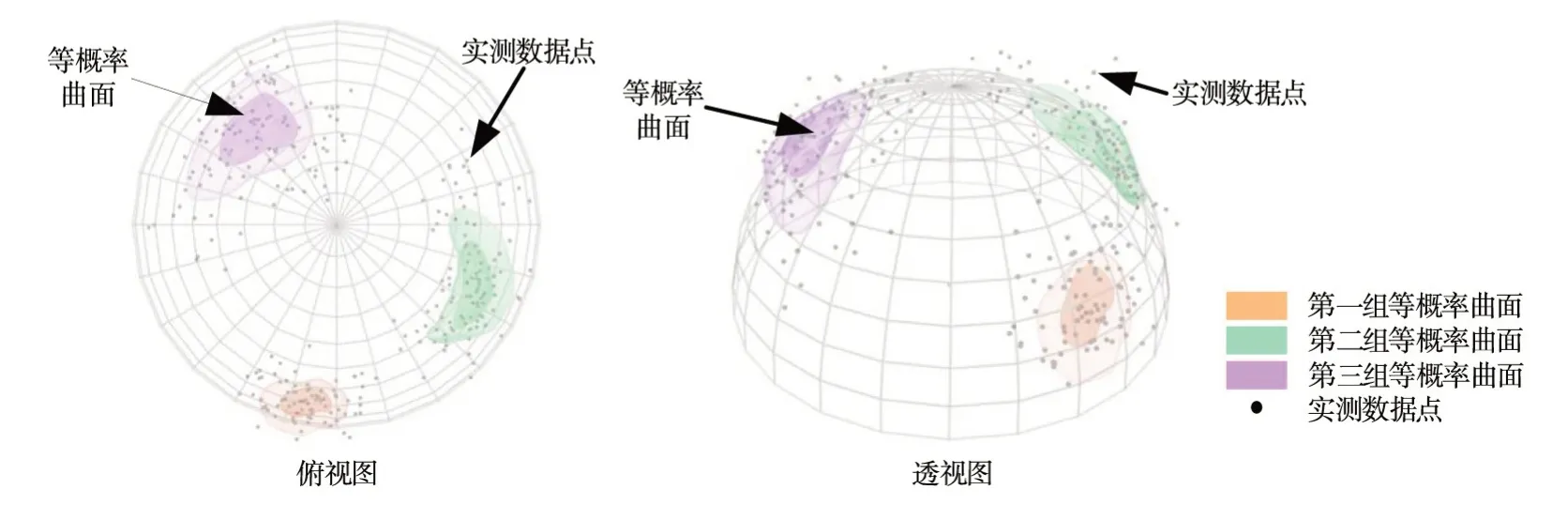
圖7 三維聯合分布概率密度估計結果

再者，結合鉆孔圖像與開挖面測窗中的裂隙數據，通過體密度估計得到三組裂隙網絡中裂隙數量分別為530、460 與470，并采用泊松過程對圓盤裂隙的中心點位置進行隨機模擬。經過擬合優度檢驗，三組裂隙的實測跡長都服從對數正態分布。假設圓盤裂隙直徑服從Gamma 分布，通過動態優化得到第一組的形狀參數為3.804，逆尺度參數為0.827，第二組的形狀參數為3.075，逆尺度參數為1.235，第三組的形狀參數為4.982，逆尺度參數為1.400。

根據所建立的概率分布可以生成多個三維離散裂隙網絡，對其中一次隨機模擬生成的范例進行可視化如圖8所示。進一步對該裂隙網絡的跡線模擬結果進行數值檢驗，采用單尾F 檢驗與雙尾t 檢驗，顯著度設置為0.05，如表1所示。F 檢驗與t 檢驗的P 值均大于顯著度，說明模擬跡長的方差和均值都與實測結果無顯著差異。提出的DFN 建模方法基于深度生成模型充分挖掘了壩基裂隙巖體內部鉆孔與開挖面測窗數據所蘊含的裂隙幾何信息，多元數據互相印證，提高了DFN 模型的可靠性，為水電工程壩基裂隙巖體的工程地質分析與決策提供了重要支撐。

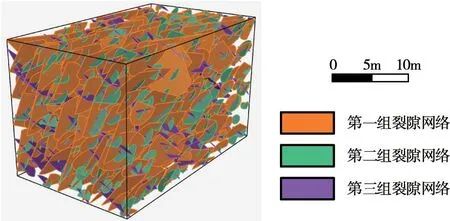
圖8 壩基三維離散裂隙網絡隨機模擬范例

表1 跡線隨機模擬范例數值檢驗

4.2 對比分析與討論首先，通過DPCAF 多參數模擬與傳統單參數模擬結果的對比分析，以及基于典型分布假設方法與DPCAF 方法的傾向與傾角二參數聯合分布估計的對比分析，驗證DPCAF 模型的準確性；其次，為了驗證DPCAF 模型對于多維參數聯合分布估計的有效性，對基于GMM 模型與DP?CAF 模型的傾向、傾角、開度多參數模擬結果進行對比分析與討論。

4.2.1 裂隙跡線數據參數相關性的單參數模擬與DPCAF 模擬對比分析 本案例采用Mendoza-Torres等［10］的文章中給出的裂隙跡線數據進行對比分析，如圖9（a）所示，該裂隙網絡為一組由張拉裂隙與剪切裂隙構成的共軛裂隙系統，包含兩組裂隙，其中一組優勢裂隙沿南北方向延伸，具備較大的跡長但裂隙數量較少，另一組裂隙沿東西方向延伸，跡長相對較小但裂隙數量較多，因此，該裂隙系統的走向與跡長具備特定的依賴關系［10］，如圖9（a）所示，其中跡長為前10%的裂隙跡線標記為黑色，其余裂隙跡線標記為藍色。跡長與走向分別進行單參數隨機模擬生成的一個范例如圖9（b）所示，采用DPCAF 模型對跡長與走向進行多參數隨機模擬生成的一個范例如圖9（c）所示。顯然，實測數據中跡長較大的裂隙主要集中于南北走向，然而，采用傳統的單參數方法模擬的大跡長裂隙沒有呈現出明顯的優勢走向，甚至有更多的大跡長裂隙為東西走向。因此，單參數模擬方法丟失了裂隙跡長與走向之間的依賴關系。相反，圖9（c）中的模擬結果與圖9（a）具備良好的一致性，因此DPCAF 模型在進行裂隙幾何參數聯合分布估計的過程中能夠良好地捕捉跡長與走向之間的依賴關系。

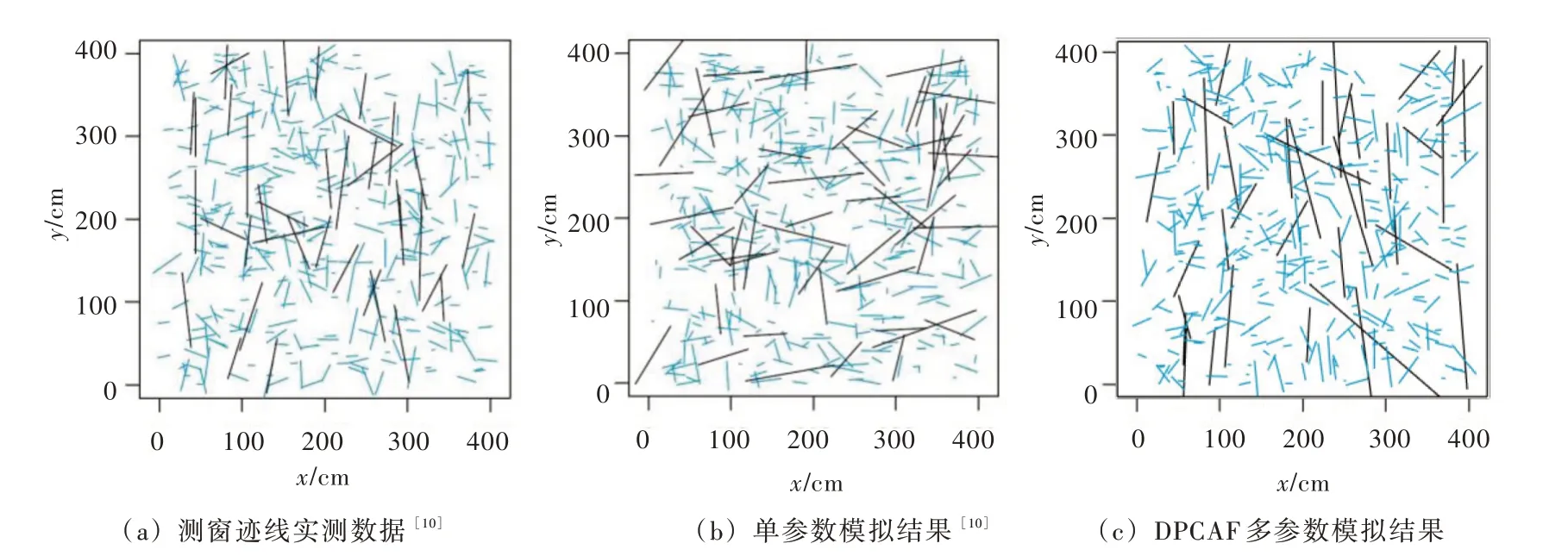
圖9 2D 裂隙網絡隨機模擬范例對比

為了將走向與跡長之間的關聯結構進行可視化，將圖9 中裂隙的幾何參數繪制于圖10（a）—（c）的散點圖中，并進一步利用Mendoza-Torres 等［10］的研究中所采用的方法，將散點圖轉換為分位數分布圖，如圖10（d）—（f）所示。分位數分布圖展示的是分位數的概率，例如，對于散點圖中橫坐標所表示的裂隙走向處于中位數的點在分位數分布圖中的橫坐標u=0.5，而散點圖中橫坐標處于四分位數的點在分位數分布圖中的橫坐標u=0.25，對于縱坐標的轉換方法同理。實測數據中兩個變量的秩相關系數為0.635，說明走向數據與跡長數據不是獨立的［10］。分位數分布圖10（d）與圖10（f）中的點都呈現出相同的分布規律，然而圖10（e）中的點趨向于離散的均勻分布，因此DPCAF 多參數模擬的結果有效地還原了走向與跡長兩個變量之間的二元結構，能夠克服傳統單參數方法難以模擬裂隙參數之間關聯關系的不足。

圖10 裂隙走向與跡長隨機模擬范例的散點圖與分位數分布圖對比

4.2.2 裂隙產狀數據二參數聯合分布的典型分布模擬與DPCAF 模擬對比分析 目前離散裂隙網絡模擬方法中，涉及到聯合分布估計的參數只有傾向和傾角參數，通常假設傾向與傾角服從雙正態分布或Fisher 分布。Shanley-Mahtab 數據集［34］為Shanley 與Mahtab 從美國亞利桑那州San Manual 銅礦收集的286 個裂隙產狀測量值。該數據集被廣泛地應用于關于產狀分布的研究中［11］。因此，本文將所提出的DPCAF 模型應用于Shanley-Mahtab 數據集中第一組與第二組產狀數據的分布估計，并與傳統方法進行對比，結果如表2所示。Fisher 分布的估計精度大于雙正態分布，但兩者的對數似然函數都小于0，而DPCAF 模型對兩組產狀數據分布估計的對數似然函數都在8 以上。可見，實測產狀數據的分布可能并不完全服從雙正態分布與Fisher 分布的假設，而DPCAF 模型的概率密度估計結果更加接近數據的實際分布。

表2 產狀數據概率密度估計精度對比

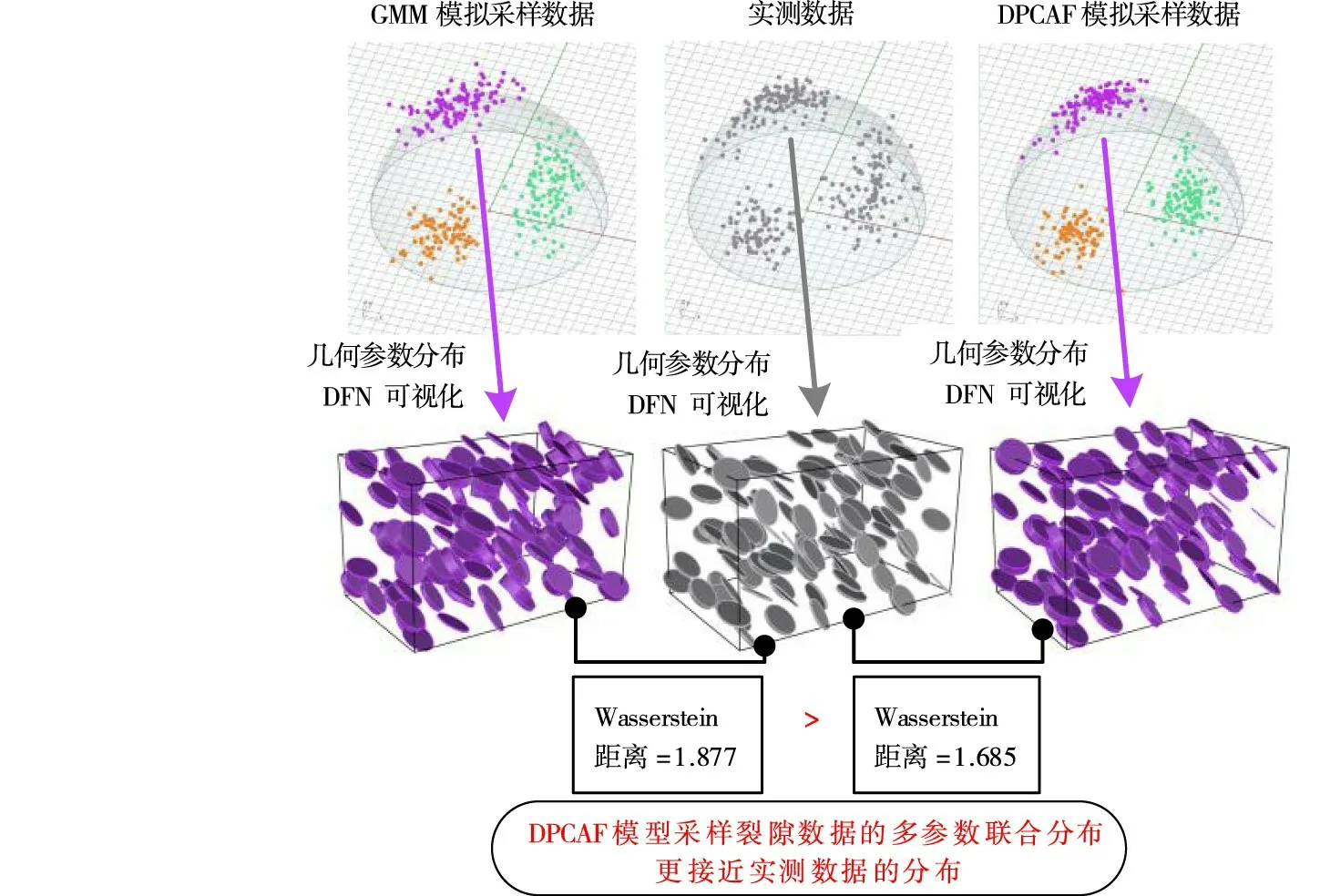
圖12 采樣模擬裂隙數據范例可視化對比

4.2.3 鉆孔圖像數據多參數聯合分布的GMM 模擬與DPCAF 模擬對比分析 為了對傾向、傾角與開度數據的概率密度估計的精度進行評價，將提出的DPCAF 模型與目前主流的有限混合模型（Finite Mixture Model）——高斯混合模型（Gaussian Mixture Model，GMM）進行對比，如圖11所示。

三維的GMM 模型的每一個分支對應的等概率密度曲面都為“置信橢球”，但由于實測裂隙開度參數的分布較為集中，對應于球坐標系下的三維空間點基本分布于開度等參球面附近，而不是呈橢球狀分布。GMM 用“置信橢球”擬合實際數據時表現出了一些系統性的偏倚，例如，圖11（b）中綠色的第二組和圖11（c）中紫色的第三組裂隙所估計的置信橢球的一端明顯向開度等參球面外側翹起。相反，DPCAF 模型可以建立任意復雜不規則形狀的分布，所估計的概率密度形狀良好地擬合了真實數據點的分布。采用評價概率密度估計的精度的常用評價指標——平均對數似然（Mean Log-Likelihood）［19］進行量化對比。其中，DPCAF 模型的平均對數似然都在21 至22左右，而GMM 模型的平均對數似然都在-6 以下，可見DPCAF 的概率密度估計精度高于GMM。

進一步對比分析GMM 與DPCAF 模型的采樣模擬的誤差，控制采集樣本的數量相同，采用模擬數據分布與實測數據分布之間的Wasserstein 距離［35］作為模擬誤差的評價指標，如表3所示。

表3 采樣模擬裂隙數據范例誤差對比

圖12 以第三組裂隙為例，分別采用球坐標可視化與DFN 可視化方法對三維數據分布建立形象直觀的表達。在DFN 可視化方法中，固定每個圓盤結構面的中心點位置和半徑，將采樣數據所包含的傾向、傾角和開度幾何參數分別賦值給不同的圓盤模型，得到虛擬的離散網絡模型，其中為了提升可視化效果將開度數據乘以500 作為圓盤的厚度，如圖12所示。可以發現，DPCAF 采樣的每一組裂隙的分布以及三維裂隙的整體分布都比GMM 的采樣結果更加接近實測數據，從而證明了本文提出的DPCAF 模型的模擬精度更高。

5 結論

裂隙幾何參數分布的估計與擬合是三維離散裂隙網絡隨機模擬的核心環節。然而，現有的DFN建模方法基于Gamma 分布、對數正態分布、Fisher 分布等典型分布對單參數的邊緣分布或傾向傾角的聯合分布進行估計，面臨著無法拓展到更多維裂隙參數的復雜聯合分布的難題。針對上述問題，本文提出了基于改進自回歸流模型的DFN 多參數模擬方法，取得了如下成果：

（1）考慮裂隙幾何參數具有優勢分組的特點改進自回歸流模型，將標準化特征空間的高斯分布改進為高斯混合分布，并結合DensityPeak 算法搜索聚類中心，提出了DPCAF（Density Peak Clustering Autoregressive Flow）模型，克服了自回歸流模型對于裂隙數據多峰分布擬合能力的不足；

（2）將自回歸流模型中基于可逆變換擬合復雜多維聯合分布的思想引入DFN 建模中，有效解決了DFN 多參數模擬所面臨的多維聯合分布的概率密度估計與采樣的核心難題，在DFN 建模的過程中同時完成多參數優勢分組與多參數概率密度估計；

（3）工程應用表明，對于實測裂隙數據的復雜聯合分布，本文提出的DPCAF 模型相比與傳統基于典型分布的估計方法具備更強的擬合能力，并且能夠有效還原多參數之間的關聯關系；DPCAF 模型相比于雙正態分布與Fisher 分布對于產狀數據的概率密度估計精度更高，相比于GMM 模型對于鉆孔圖像中的傾向、傾角、開度數據聯合分布的概率密度估計的平均精度更高，且采樣結果的誤差縮小了7.84%。因此，DPCAF 模型能夠有效提高多參數擬合的準確性，保證DFN 建模的精度。

本文提出的改進自回歸流模型能夠為工程分析過程中涉及到的多維聯合概率密度估計問題提供一種新的技術手段［36-37］。此外，隨著水電工程地質勘測與感知技術的不斷進步［38］，未來將可能獲取更多種類的裂隙數據，可以將其引入DFN 多參數模擬中進一步提升裂隙網絡模型的可靠性。