樁承式高速鐵路路基的地震反應特性研究

宋永山,高 盟,彭曉東,徐 曉

(1.山東科技大學 山東省土木工程防災減災重點實驗室,山東 青島 266590;2.山東科技大學 土木建筑學院,山東 青島 266590)

0 引言

隨著我國高速鐵路建設快速發(fā)展,高鐵線路更加密集,而我國位于兩大地震帶,地震頻發(fā)對高鐵運行帶來嚴重威脅[1],地震荷載作用下高鐵的運行安全受到了廣泛關注[2-3]。尤其是軟土地區(qū),樁承式路基以其優(yōu)異性能在高速鐵路建設中得到了推廣和應用[4-6],因此研究地震荷載作用下樁承式路基的地震反應特性具有重要意義。

然而,目前對樁承式路基的研究多集中在列車移動荷載引起的路基動力反應特性,如周順華等[7]分析列車瞬時沖擊荷載作用下樁承式高速鐵路路基土拱安定性,確定了土拱不發(fā)生累積變形破壞的荷載臨界值;Thach等[8]建立樁承式路基有限元模型,分析了加固后路基與天然地基在列車移動荷載作用下的動力響應作用機理,發(fā)現路堤是控制振動響應的主要因素,且高頻波會在樁支撐的路堤系統(tǒng)中被捕獲和消散,從而顯著降低路堤外的振動振幅;付強等[9]利用有限元法研究了列車荷載作用下PCC樁復合地基的動力響應,研究表明路堤內振動波遠低于枕木處振動幅值,通過路堤、樁體和地基振動響應曲線體現了振動波在路堤系統(tǒng)各部分的傳播特點;高廣運等[10]通過2.5維有限元建立列車-軌道-路基整體動力分析模型,發(fā)現CFG復合路基減小了路堤邊緣的高頻振動,提高了路堤邊坡的動力穩(wěn)定性;薛富春等[11]精細化分析了軌道-路基-地基耦合系統(tǒng)的非線性振動響應。

而對地震荷載作用下路基動力反應特性的研究主要針對高速鐵路橋梁樁基和公路路基。如陳令坤等[12]基于有限元法研究了不同地震強度下是否考慮樁土作用的高鐵簡支梁橋動力響應;劉闖等[13]通過振動臺試驗,分析了地震動強度下大直徑橋梁嵌巖樁基礎加速度、相對位移、彎矩等響應特性和損傷情況;趙建斌等[14]建立三維樁承式公路路基數值模型,研究了水平地震荷載作用下土工格柵抗拉模量和樁間距的影響;薛富春等[15]建立三維數值分析模型研究了橋梁-橋墩-樁基礎-地基為一體的耦合系統(tǒng)的非線性地震反應。對樁承式高速鐵路路基地震反應特性的研究鮮有文獻報道。

1 計算模型及參數

1.1 有限元模型建立

依據《高速鐵路設計規(guī)范》(TB10621-2009)[16],本文采用CRTSⅠ型板式無砟軌道,軌道結構從上向下依次為:鋼軌、軌道板、CA砂漿層和底板。基床表層采用級配碎石,厚度為0.4 m,基床底層采用A、B組土,厚度為2.3 m,路堤采用A、B、C組土,厚度為2 m。模型剖面示意圖如圖1所示。

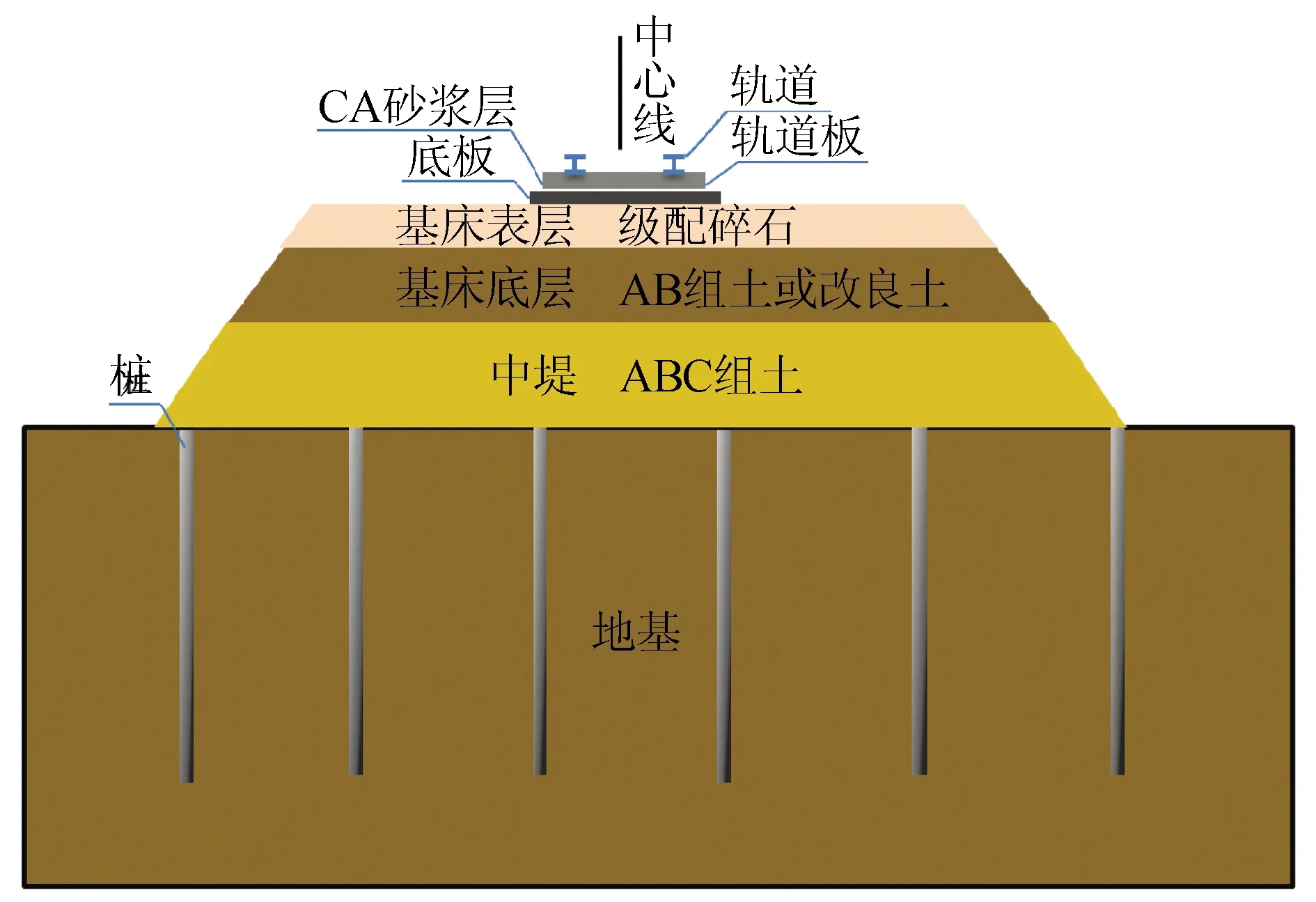
圖1 模型剖面示意圖Fig.1 Profile of calculation model

基于ABAQUS數值計算軟件,建立軌道結構-路基-地基三維有限元模型,如圖2所示。模型沿線路縱向的長度52 m,地基表面寬度52 m,總高度27.706 m。此模型系統(tǒng)由鋼軌-扣件-軌道板-CA砂漿層-底板-基床表層-基床底層-路基本體-樁-地基組成。其中,鋼軌采用60 kg·m-1標準鋼軌,軌距為1.435 m;扣件支點間距為0.65 m;鋼軌和扣件之間采用彈簧阻尼器進行模擬,扣件剛度的橫向、垂向及縱向等效剛度分別為37.5、25、37.5 kN·m-1,阻尼系數分別為30、37.5、30 kN·s·m-1;軌道板、CA砂漿層、路基和地基均采用8結點實體單元。將地基土視為彈塑性材料,在樁-土界面上設置接觸,對土體采用D-P模型,樁體采用彈性模型,樁-土之間設置接觸對,包括法向作用(“硬接觸”)和切向作用(摩擦特性為“罰”),單元選擇線性減縮積分單元(C3D8R)。

圖2 有限元計算模型Fig.2 Finite element computing model

為得到軌道、路基的振動響應規(guī)律,本文設置4個監(jiān)測點,分別為軌道(監(jiān)測點1)、基床表層(監(jiān)測點2)、路肩邊(監(jiān)測點3)和路基坡腳(監(jiān)測點4),如圖3所示。

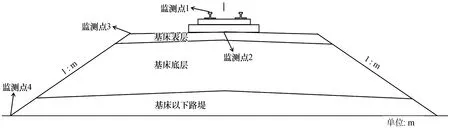
圖3 監(jiān)測點布置示意圖Fig.3 Schematic diagram of monitoring point layout

1.2 地震荷載施加

夏棟舟等[17]在計算結構抗震性能分析時,將地震波加速度直接從模型底部輸入,得到了合理的結果,本文亦采用該方法。從模型底部輸入Imperial Vally地震波,選取抗震設防烈度為Ⅶ度,根據抗震設防烈度和地震動峰值加速度值的對應表(表1),將地震波峰值調整至0.1g,其水平方向加速度時程曲線如圖4所示。取地震加速度時程曲線2～3.2 s加速度從模型底部輸入,經計算,此時地面的加速度峰值約為0.13g,相當于烈度為Ⅶ度的地震。

圖4 Imperial Vally 地震加速度時程曲線Fig.4 Acceleration time history of Imperial Vally

表1 抗震設防烈度和地震動峰值加速度值Ag對應表Table 1 Ag corresponding table of seismic fortification intensity and peak acceleration of ground motion

1.3 邊界條件

地震荷載作用下的動力分析屬于半無限空間問題,為減小誤差,需要在邊界上設置人工邊界。杜修力等[18]提出在邊界每個方向添加單向彈簧-阻尼元件,以黏性阻尼吸能作用和彈簧剛性恢復作用模擬無限介質對近場的影響。采用其方法,地基四個側面采用黏彈性邊界,地基底部采用固定豎向位移的形式,模擬波從有限域向無限域傳播。三維黏彈性人工邊界的彈簧-阻尼元件參數為:

法向:

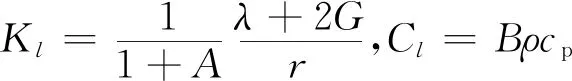
美國FATCA的CAA，雖然形式上是雙邊的對等協(xié)議，但實質上主要是向美國單向交換信息，很不公平。美國以推進FATCA為理由，至今未簽署，也未承諾執(zhí)行AEOI的CRS MCAA。美國在受益所有人審查和登記方面并未形成有效的國內立法，其結果，就是美國讓上百個國家在其主導的規(guī)則下為國際稅收信息自動交換相互博弈，卻把自己保護起來成為安全島，使美國成為全世界最大的避稅港之一。

(1)

切向:

(2)

式中:ρ為介質密度;cp=[(λ+2G)/ρ]0.5,cs=(G/ρ)0.5分別為壓縮波和剪切波的波速;A為平面波和散射波的幅值含量的比值;B為物理波速與視波速之間的關系;A和B可以通過數值試驗經驗獲得,一般A=0.8,B=1.1;長度r為近場結構幾何中心到該人工邊界點所在邊界線或面的距離。

1.4 模型計算參數

參考文獻[19],有限元模型由鋼軌-扣件-軌道板-CA砂漿層-底板-基床表層-基床底層-路基本體-地基組成。參考文獻[19],除地基土外計算模型各組成部分采用彈性本構,模型邊界采用三維黏彈性人工邊界,計算參數列于表2。

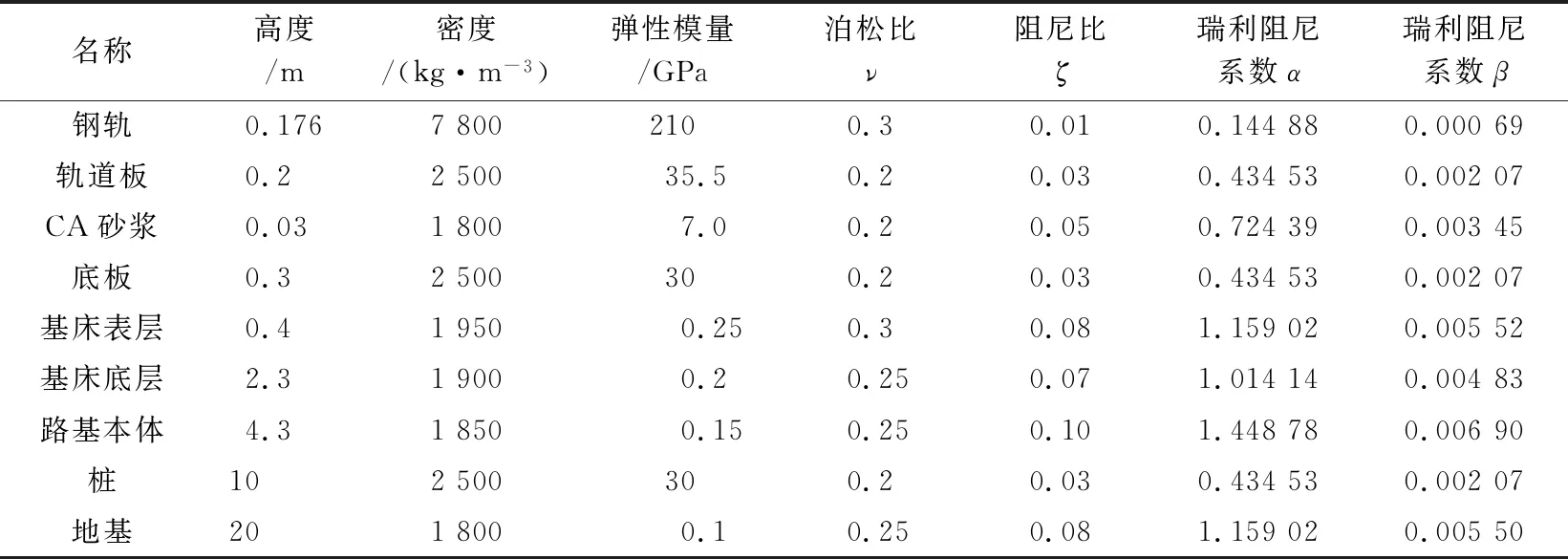
表2 有限元模型計算參數Table 2 Parameters of the finite element computing model

2 計算模型驗證

軌道-路基-地基有限元模型的有效性是結果準確的必要前提。董亮等[20]對高速鐵路無砟軌道路基基床表層頂面豎向動應力進行了實測和數值模擬。對已建立的模型進行有效性驗證,采用相同材料參數及列車軸重,得到基床表層豎向動應力對比圖。如圖5對比可知,本文所得基床表層動應力時程曲線與文獻[20]結果基本吻合。

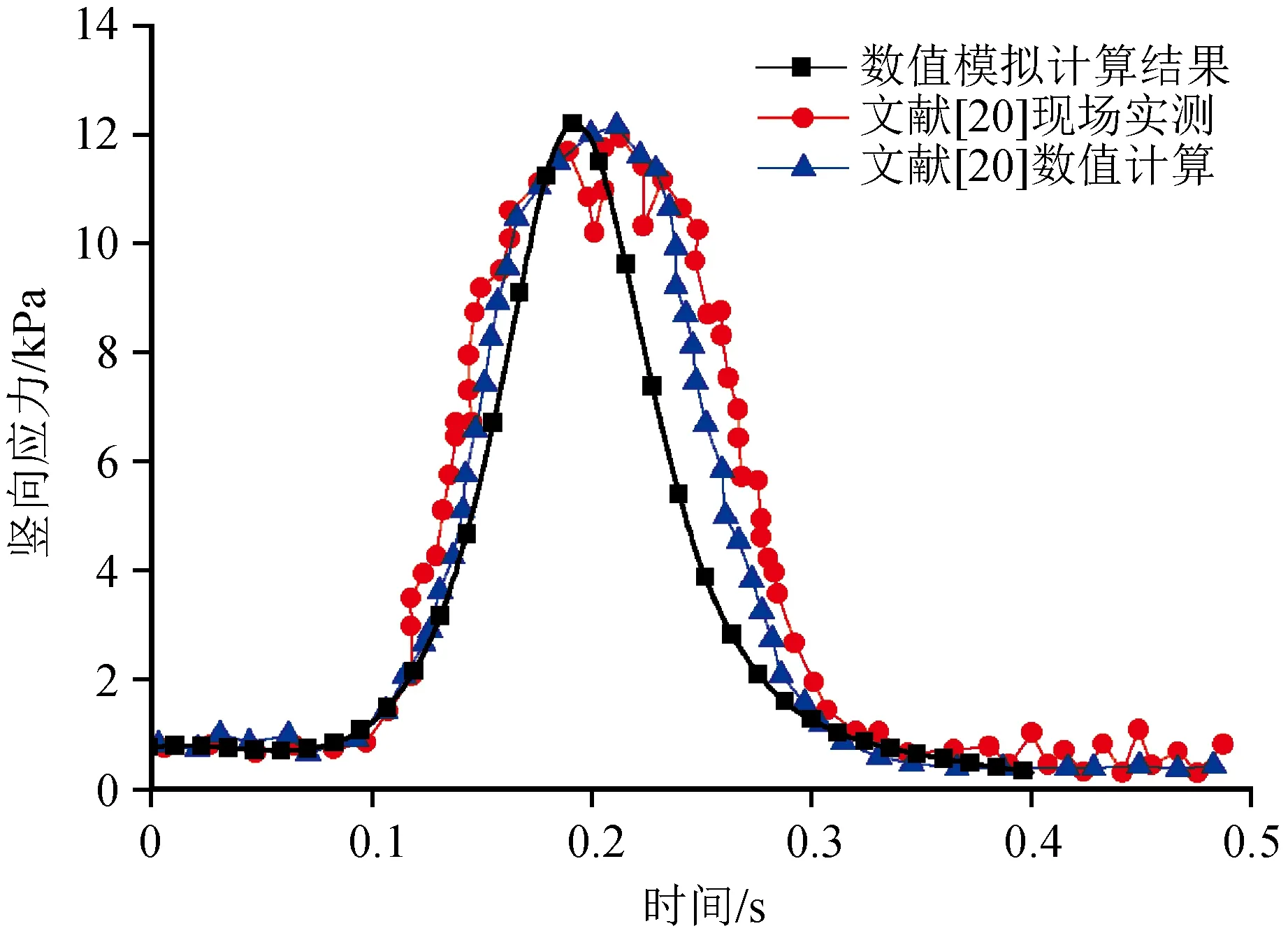
圖5 與文獻[20]對比結果Fig.5 Comparison between results of this paper and reference[20]

3 自由式路基振動響應規(guī)律

3.1 位移時程曲線分析

在自由式路基下施加地震荷載,研究軌道、路基的振動響應規(guī)律。如圖6所示,為地震荷載作用下軌道和路基的位移時程曲線。對軌道不同方向,軌道x方向位移變化最大,最大位移為13.33 mm;z、y向分別為 2.62 mm、0.49 mm。水平x方向過大的位移無疑會在地震時導致軌道變形,威脅列車運行安全,如1976年中國唐山大地震(http://pic.enorth.com.cn/003/019/140/00301914051_6d98c759.jpg),需引起工程施工的重視。而對于路基各結構層,路基坡腳、路肩邊、基床表層,從下往上z向位移最大值分別為12.6 mm、4.44 mm、0.5 mm,減小速度明顯,說明路基在豎直方向有較好的減震作用。

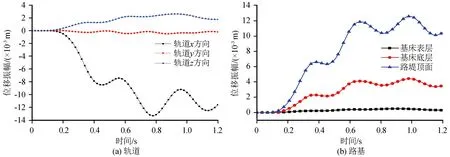
圖6 軌道和路基位移時程曲線Fig.6 Displacement time history curves of rail and subgrade

3.2 加速度時程曲線分析

圖7為地震荷載作用下軌道和路基的加速度時程曲線。與位移時程曲線規(guī)律一致,軌道x方向加速度振幅最大,振幅峰值為0.71 m/s2,z方向為0.11 m/s2,y方向為0.09 m/s2。路基坡腳、路肩邊、基床表層,從下往上加速度逐漸減小,z向加速度最大值分別為0.54 m/s2、0.2 m/s2、0.06 m/s2。振動加速度幅值在路基中衰減明顯。

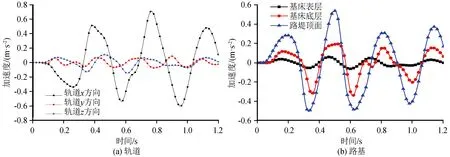
圖7 軌道和路基加速度時程曲線Fig.7 Acceleration time history curves of rail and subgrade

3.3 頻譜分析

頻譜分析是抗震分析的重要手段之一,地震荷載作用下軌道和路基加速度頻譜曲線如圖8所示。得到地震作用下軌道和路基的頻率主要集中在0～10 Hz,為低頻振動。由圖可知,軌道不同方向主頻值及加速度值并不相同,x、z方向頻譜曲線較為相似,主導頻率均為2.9 Hz,頻率范圍為0～10 Hz,加速度最大值分別為0.39 m/s2、0.003 8 m/s2;y方向主導頻率為4.4 Hz,頻率范圍為0～15 Hz,加速度最大值為0.003 7 m/s2。路基各層主導頻率一致,均為2.9 Hz;但基床表層主要頻率縮小到0～5 Hz,說明路基吸收了部分地震能量。而圖10為輸入地震波水平方向加速度頻譜曲線,頻率主要集中在0～15 Hz。x方向主導頻率為0.8 Hz,加速度最大值為0.3 m/s2,地震波y方向主導頻率為0.4 Hz,加速度最大值為0.29 m/s2。

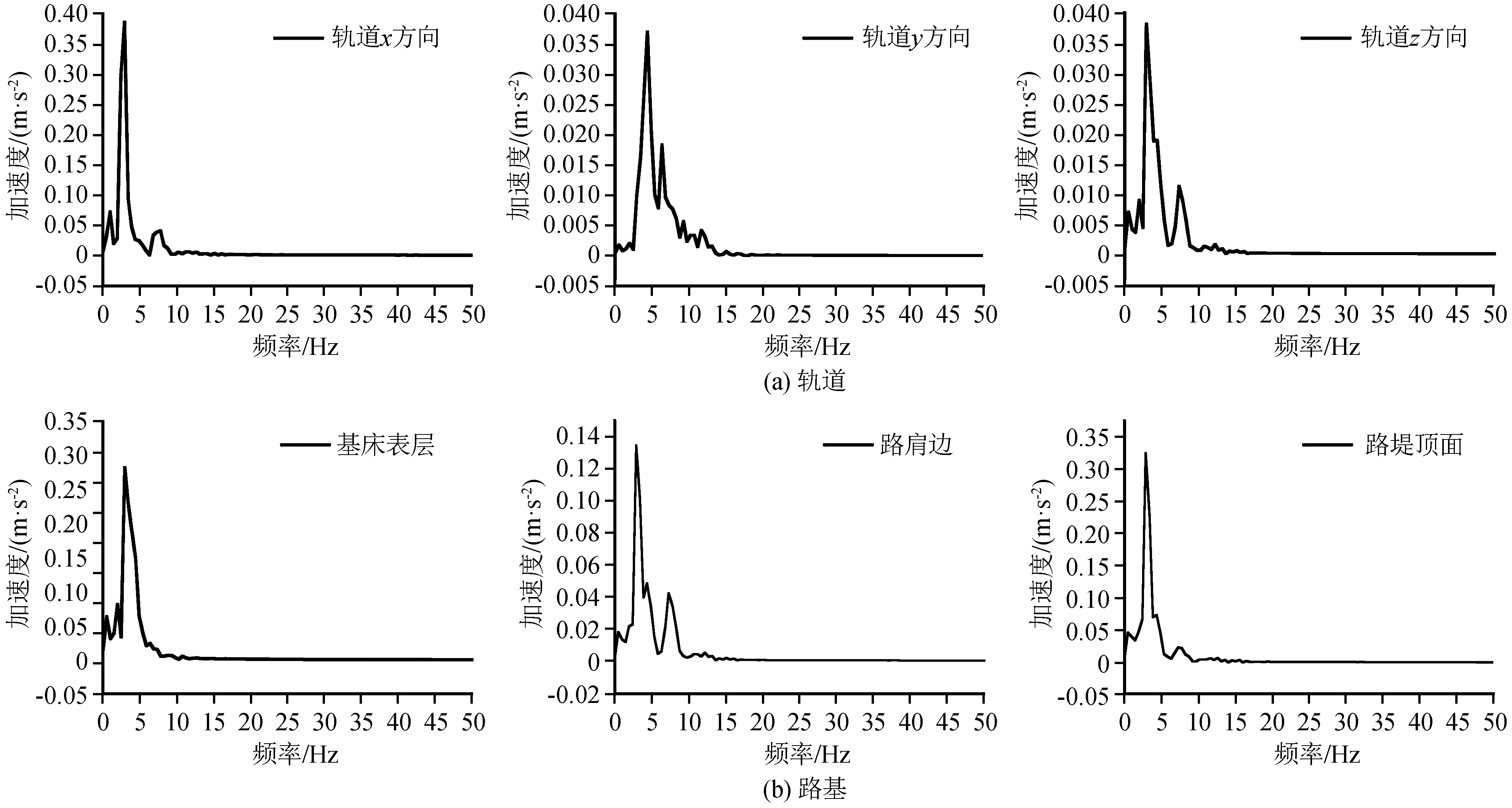
圖8 軌道和路基加速度頻譜曲線Fig.8 Acceleration spectrum curves of rail and subgrade

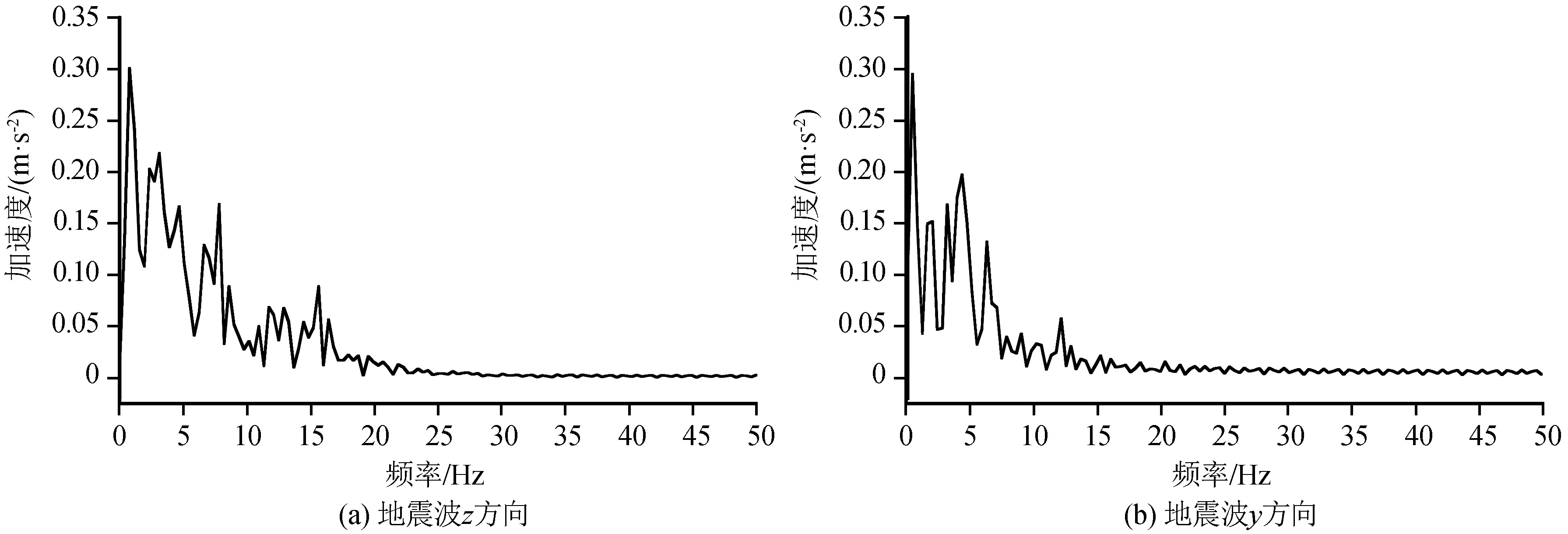
圖9 地震波加速度頻譜曲線Fig.9 Acceleration spectrum curves of earthquake wave

對比兩圖可知,地震波頻譜曲線主導頻率在1 Hz以下,且主頻不唯一,頻率范圍為0.4～20 Hz。而軌道和路基頻譜曲線主導頻率比較單一,主頻范圍為2.5～7.5 Hz,頻率范圍為0～15 Hz。經過地基傳播介質,地震波多個主頻及15～20 Hz頻率等特征的能量被吸收。

4 樁承式路基參數分析

4.1 樁徑

為分析樁徑對高速鐵路路基抗震影響,設置樁間距為2 m,樁長為10 m,樁徑為0.6 m,0.8 m,1.0 m及1.2 m進行計算,分析不同樁徑時軌道和軌道中心正下方路基各層位移幅值變化以及加速度幅值變化情況。其中,樁徑為0時表示地震荷載作用下的自由式路基。

由圖10可知,鋼軌x、y方向位移幅值隨樁承式路基樁徑增大而增大,而z方向位移幅值較自由式路基有所減小。對于路基各層,樁承式路基位移幅值明顯減小,且隨樁徑增大而減小,但減小速率逐漸放緩。對比自由式路基,樁承式路基作為復合地基,抗彎剛度增大,且隨樁徑增大,復合地基置換率越大,路基、鋼軌豎向位移減小。而樁體彈性模量增大導致地震能量吸收減小,則成為軌道水平位移增加的主要原因,樁承式路基的存在反而增加了列車脫軌的風險。

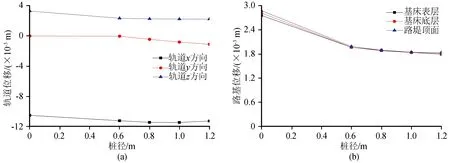
圖10 樁徑對軌道和路基各層位移幅值影響Fig.10 Influence of pile diameter on displacement of rail and subgrade

圖11為軌道、路基加速度幅值隨樁承式路基樁徑變化情況。樁承式路基對地震加速度有較好的減弱作用,但并不是隨著樁徑增大而持續(xù)增強,當樁徑過大,復合地基整體剛度過大時,軌道、路基加速度響應又開始增大。軌道x、z方向加速度幅值減小明顯,但當樁徑超過1.0 m時,軌道x方向又開始增大。軌道z方向加速度幅值最低點出現在樁徑0.8 m。而路基各層位移幅值同樣隨樁徑增大先減小后增大。

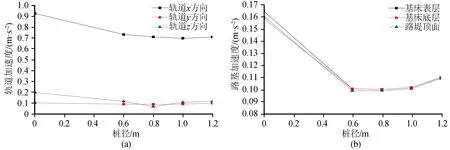
圖11 樁徑對軌道和路基各層加速度影響Fig.11 Influence of pile diameter on acceleration of rail and subgrade

4.2 樁長

設置樁間距為2 m,樁徑1.0 m,對樁長分別為8 m,10 m,12 m,14 m的樁承式路基的動力響應特性分析。

圖12為軌道和路基位移幅值隨樁長變化規(guī)律,樁承式路基軌道x方向位移幅值隨樁長增大而增大,而y、z方向只有較小幅度的減小作用。同樣,樁體增加對軌道x方向位移仍存在增大效應。對于路基各層,樁承式路基中各監(jiān)測點位移幅值明顯減小,樁長越長,樁側阻力越大,z向位移幅值越小。

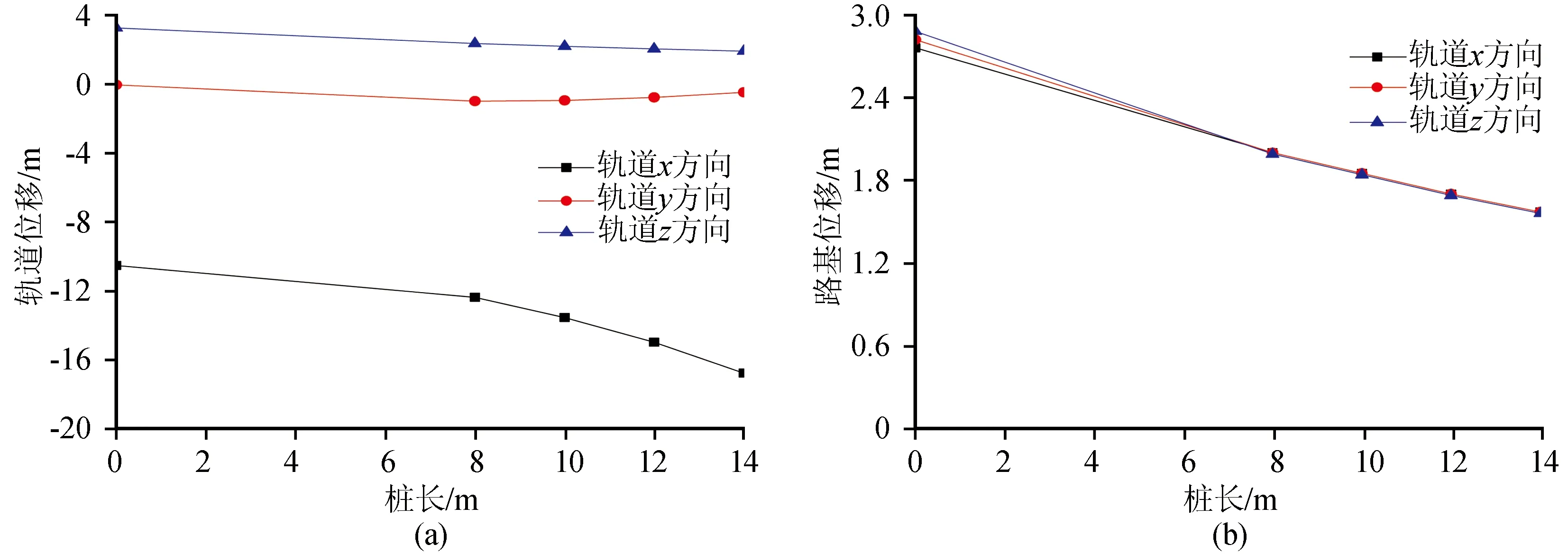
圖12 樁長對軌道和路基各層位移幅值影響Fig.12 Influence of pile length on displacement of rail and subgrade

對比自由式路基,樁承式路基軌道、路基加速度幅值減小明顯,如圖13所示。但軌道x方向加速度幅值在樁長為8 m時最小,之后隨樁長增大而增大。軌道z方向、路基各層加速度幅值隨樁長增大有效減小,樁長越大,樁土有效接觸面積越大,地震加速度吸收越多,軌道路基z向加速度越小。

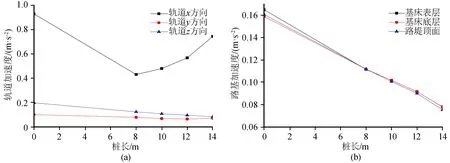
圖13 樁長對軌道和路基各層加速度影響Fig.13 Influence of pile length on acceleration of rail and subgrade

4.3 樁間距

樁間距同樣是影響樁承式路基減震效果的重要因素。設置樁長為10 m,樁徑1.0 m,樁間距分別為1.5 m、2 m、2.5 m和3 m進行計算。

圖14、15為軌道和路基振動響應隨樁間距變化規(guī)律。研究表明在2.5D范圍樁間距內群樁效應明顯,因此,軌道x、y方向位移幅值隨樁間距增加先增大后減小,在樁間距2 m時出現最大值,樁間距的加大對樁體彈性模量的集中增大起到了一定的減弱作用,因此超過2 m后樁間距越大,x、y方向位移幅值越小。而樁間距不斷增大對z向位移的減震效果卻起到了減弱作用,路基各層位移幅值隨樁間距增大先減小后增大,樁間距2 m時位移幅值出現最小值。對于加速度幅值,軌道x、z方向隨樁間距增大呈現先減小后增大的趨勢。且兩者在樁間距為2 m時出現最小值。路基各層加速度幅值隨樁間距增大先減小后增大,最低點在1.5 m。

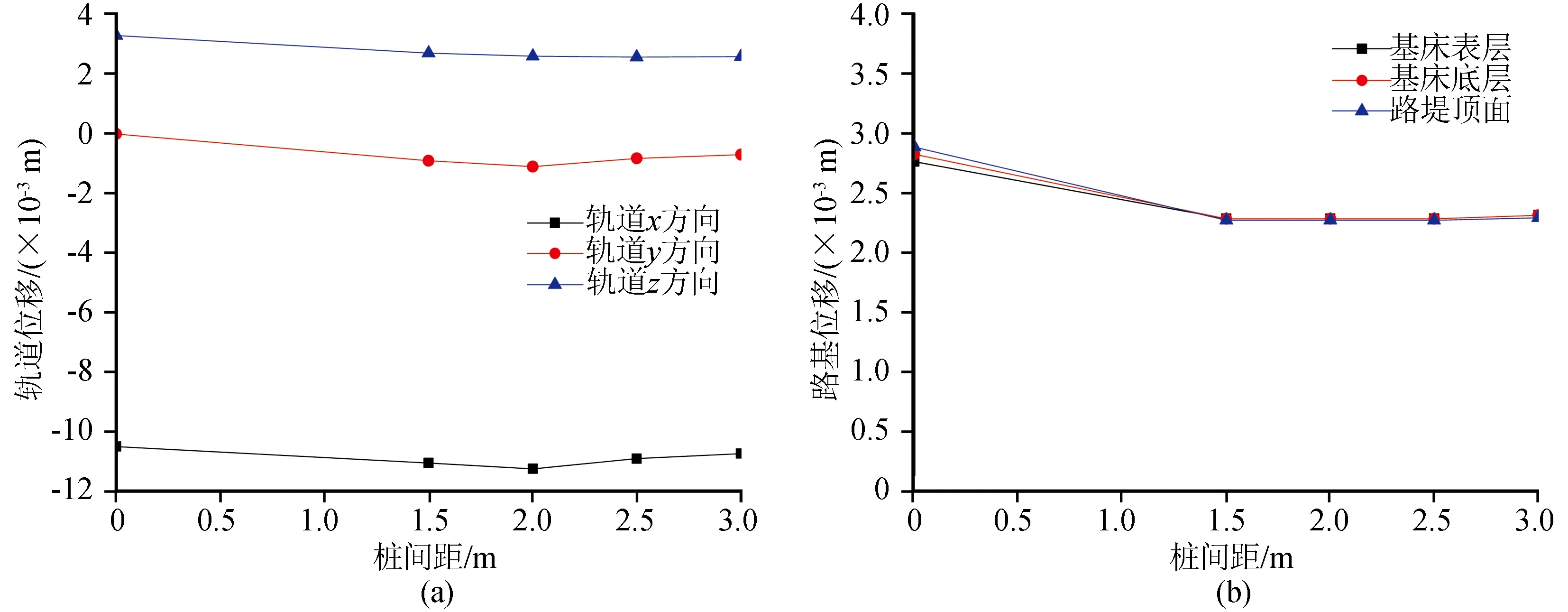
圖14 樁間距對軌道和路基各層位移幅值影響Fig.14 Influence of pile spacing on displacement of rail and subgrade

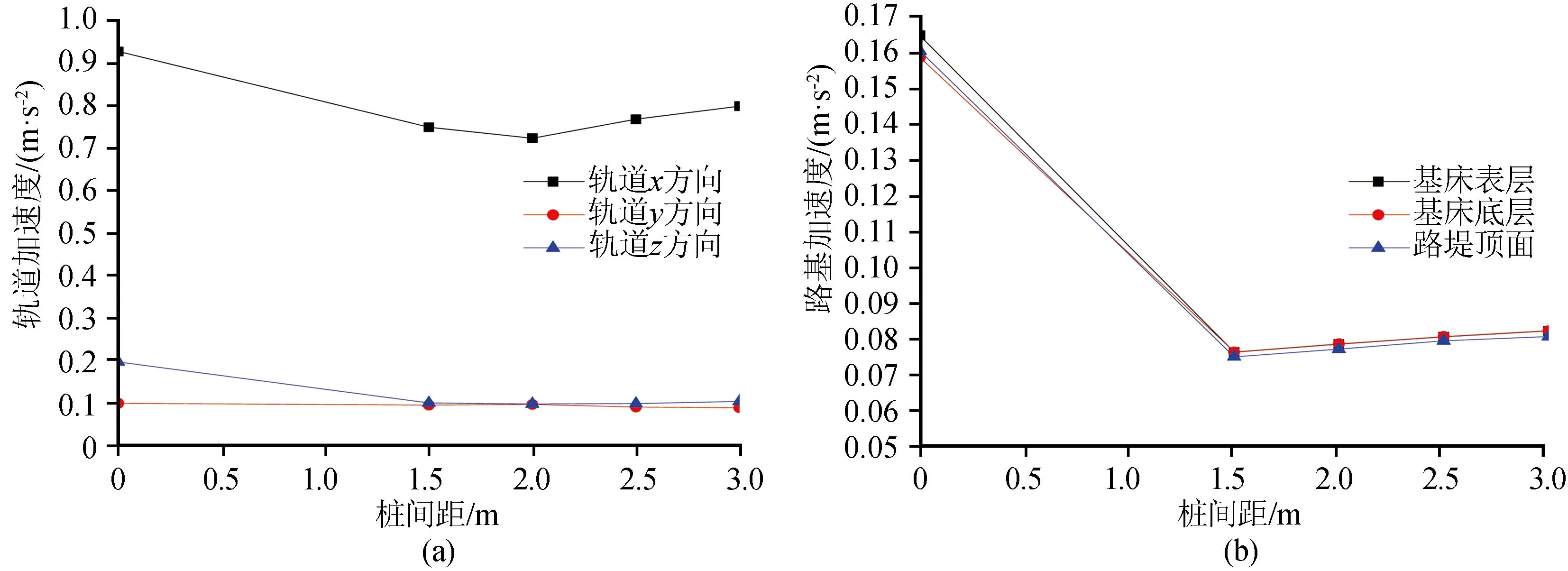
圖15 樁間距對軌道和路基各層加速度影響Fig.16 Influence of pile spacing on acceleration of rail and subgrade

4.4 樁身材料屬性

設置樁間距為2 m,樁長為10 m,樁徑1.0 m,樁彈性模量分別為10 GPa、15 GPa、20 GPa、25 GPa和30 GPa進行計算,分析不同樁彈性模量時軌道和路基各層位移幅值及加速度幅值變化。

由圖16可知,軌道x方向位移幅值隨樁彈性模量增大而增大,同樣證實,樁彈性模量增大使地基剛度變大是導致樁承式路基較自由式路基軌道橫向位移變大的原因。而軌道z向位移幅值隨樁彈性模量增大而減小。路基各層z向位移幅值隨樁彈性模量增大逐漸減小。

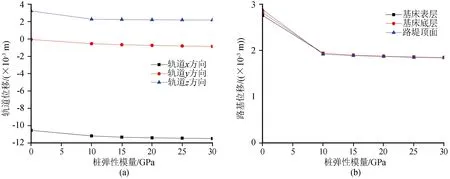
圖16 樁彈性模量對軌道和路基各層位移幅值影響Fig.16 Influence of pile elastic modulus on displacement of rail and subgrade

由圖17可知,樁承式路基狀體彈性模量增大有效減小地震加速度。軌道x、z向加速度隨樁彈性模量增大而減小,路基各層加速度也隨樁彈性模量增大而逐漸減小,但減小速率很小。樁體彈性模量增大到10 GPa后,路基、軌道加速度減弱效果便不再明顯。

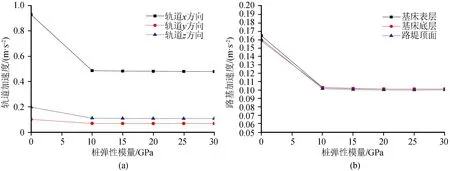
圖17 樁彈性模量對軌道和路基各層加速度影響Fig.17 Influence of pile elastic modulus on acceleration of rail and subgrade

5 結論

本文建立地震荷載作用下高鐵路基三維有限元模型,分析了自由式路基的振動響應規(guī)律,并對樁承式路基的樁體參數進行分析,得到了一些具有工程應用價值的結論。

(1) 地震荷載作用下,自由式路基軌道x方向位移變化最大,最大位移為13.33 mm;加速度振幅也最大,最大值為0.71 m/s2;而對于路基各結構層,從下往上位移幅值、加速度幅值減小明顯;頻譜曲線表明,軌道和路基主頻單一,主導頻率范圍為2.5～7.5 Hz,主要為低頻振動,經過地基傳播介質,地震波多個主頻及15～20 Hz頻率等特征的能量被吸收。

(2) 地震荷載作用下,樁承式路基對x方向位移幅值、加速度幅值反而有增大作用,可能會導致列車脫軌;但對路基及軌道z向有較好的減小作用,有利于減小沉降。

(3) 綜合分析各項樁體參數變化對地震荷載作用下樁承式路基的動力響應,最佳樁徑約為0.8 m,最佳樁長為8～10 m,最佳樁間距為1.5～2 m,最佳樁彈性模量為20 GPa。