一種LCC諧振變換器的參數設計方法

廖鴻飛，帥定新，龍濤元

（1.中山火炬職業技術學院光電信息學院，廣東 中山 528400；2.攀枝花學院智能制造學院，四川 攀枝花 617000）

諧振變換器由于能實現功率器件的軟開關，效率較高，因此得到了廣泛應用。通常高壓靜電除塵等高壓大功率輸出場合[1-2]采用LCC諧振變換器，而在中小功率場合采用LLC諧振變換器[3]。但是近年來，研究者發現相對于LLC諧振變換器，LCC諧振變換器具有更好的輕載特性和更寬的輸出電壓范圍，因此LCC諧振變換器在LED驅動等中小功率場合的應用日益增多[4-6]。LCC諧振變換器通常有電感輸出濾波[7]與電容輸出濾波[8]兩種拓撲結構。電容輸出濾波結構元件數量少，副邊二極管可以實現零電流關斷[9]，更適于中小功率場合[10]。在工作模式方面，LCC諧振變換器有電流連續模式和電流斷續模式，電流連續模式的LCC諧振變換器諧振網絡呈現感性，可以使開關管實現零電壓開通，因此適合于以MOSFET作為主開關管[9]的中小功率場合。

目前，許多學者對電流連續模式的電容輸出濾波LCC諧振變換器原理及參數設計方法進行了研究，提出了變換器的等效電路[8，11]和參數設計方法[12-13]，但這些設計分析方法都忽略了死區時間對變換器的影響，只是根據預先假設的諧振阻抗角來計算LCC諧振變換器的諧振網絡參數，而諧振阻抗角過大會導致諧振網絡有較大的無功環流，效率較低，諧振阻抗角太小可能導致無法實現軟開關，因此根據經驗預設阻抗角無法保證變換器的參數是最優的[14-15]，也就無法保證效率是最高的。要實現變換器參數的優化，需要尋找到阻抗角設置的約束條件，使LCC諧振變換器在實現軟開關的同時，諧振阻抗角最小，減小變換器的損耗。

本文通過分析電容輸出濾波的半橋LCC諧振變換器的死區時間、諧振阻抗角與損耗之間的關系，提出了死區時間和最小阻抗角的選擇方法，使得變換器在實現軟開關的條件下，減小了變換器的損耗，提高了變換器的效率。根據該方法設計的160 W樣機效率達到94.2%。

1 電容輸出濾波的LCC諧振變換器工作原理

圖1所示為電容輸出濾波的半橋LCC諧振變換器拓撲結構，Q1，Q2為半橋開關管，以50%的占空比互補導通；DQ1，DQ2分別為 Q1，Q2的寄生體二極管；C1，C2分別為 Q1，Q2的寄生電容；Ls，Cs，Cp構成諧振網絡；D1，D2，D3，D4構成次級側全橋整流電路；變壓器原副邊匝比為n：1；Co為輸出濾波電容；Ro為負載電阻。其穩態工作波形如圖2所示，圖中φ為諧振網絡的阻抗角，θ為副邊二極管的導通角。

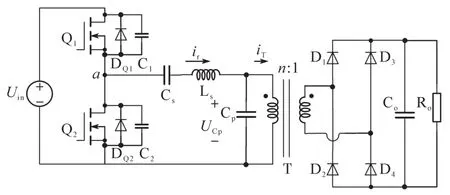
圖1 電容輸出濾波LCC諧振變換器原理圖Fig.1 LCC resonant converter with capacitive output filter

圖2 LCC諧振變換器的穩態工作波形Fig.2 Waveforms of LCC resonant converter

變換器穩態工作時的工作模態如下：

1）模態1（t0—t1）：初始狀態t0時，Q1處于導通狀態，Q2處于關斷狀態，副邊二極管D2，D3導通，半橋中點電壓Ua為輸入電源電壓，并聯諧振電容Cp兩端電壓被輸出電壓鉗位，電壓為-nUo，Ls，Cs諧振。由于此時諧振電流為負值，因此其瞬時功率p=ui＜0，諧振網絡將能量倒送回電源，形成無功環流。

2）模態2（t1—t2）：在t1時刻，諧振電流過零，副邊二極管全部截止，諧振電流開始給并聯諧振電容Cp充電，到t2時刻，并聯諧振電容Cp的電壓上升到nUo。

3）模態 3（t2—t3）：在 t2時刻，副邊二極管 D1，D4導通，Cp兩端電壓被輸出電壓鉗位，Ls，Cs與負載形成諧振，輸入電源的能量通過諧振網絡和變壓器傳遞給負載。

4）模態 4（t3—t4）：在 t3時刻，Q1，Q2關斷，變換器進入死區時間，諧振電流將通過Q1，Q2的寄生電容 C1，C2形成回路，諧振電流ir給 C1充電，使其電壓逐漸上升，給C2放電，使其電壓逐漸下降，當C2兩端電壓逐漸下降到零，下管Q2的寄生體二極管DQ2將導通，忽略二極管壓降，Q2兩端將鉗位至0 V。在t4時刻給Q2柵極一個高電平，Q2將實現零電壓開通。

其后變換器進入另一半工作周期，其工作原理與上述半個周期相似，不再詳述。

2 LCC諧振變換器的損耗及軟開關分析

2.1 LCC諧振變換器的阻抗角與損耗分析

從圖2的穩態工作波形分析可以看出，為了保證開關管能實現零電壓開通，諧振網絡通常呈現感性，即諧振電流滯后于電壓，這使得在每半個周期中，諧振網絡都有一段時間向電源輸送能量，即無功環流。其無功功率為

式中：Ur為諧振網絡輸入電壓的有效值；Ir為諧振電流的有效值。

從式（1）可見，阻抗角φ越大，諧振網絡中無功功率越大，也就是無功環流越大。由于線路中存在寄生電阻，因此無功功率的流動將在電路中產生導通性損耗。而電容輸出的LCC諧振變換器的開關管均為零電壓開通，輸出二極管都為零電流關斷，因此導通性損耗是LCC諧振變換器的主要損耗。

由于變換器最終需要向負載提供有功功率，因此對于LCC諧振網絡，其輸出的有功功率為

由式（2）可以得到諧振電流有效值為

假設電流回路中總的寄生電阻為r，則電流所造成的導通損耗為

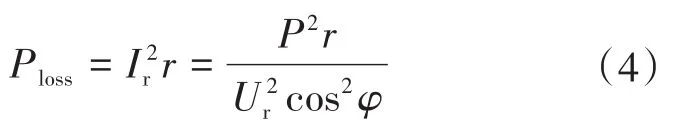
由式（4）可以得到損耗與阻抗角之間的關系曲線如圖3所示。從圖中可見，電路中的導通損耗會隨著阻抗角的增大而增大，當阻抗角超過一定值時，損耗將急劇增加。因此減小阻抗角可以降低變換器的損耗。

圖3 損耗與阻抗角之間的關系曲線Fig.3 Relationship between power loss and impedance angle

2.2 LCC諧振變換器的軟開關條件

從圖3中看到，減小諧振阻抗角可以減小損耗，提高變換器效率。然而，阻抗角太小，將使得開關管換流時的電流減小，不利于開關管實現零電壓開通。為了能夠在減小阻抗角的同時保證開關管實現零電壓開通，實現諧振網絡參數的優化，需要對LCC諧振變換器的軟開關條件進行分析。對穩態時工作模態4的分析可知，開關管要實現零電壓開通，需要在換流期間，也就是死區時間內完成開關管輸出結電容的充放電，分析圖2可知Q1在t0時刻導通，對應的電流為ir（t0），因此要實現軟開關條件，必須滿足：

式中：td為死區時間；Coss為開關管的輸出結電容。

諧振電流近似為正弦波，因此可假設諧振電流為

式中：ILrmax為諧振電流最大值；Ir為諧振電流有效值；φ為諧振網絡阻抗角。

諧振電流最大值為[8]

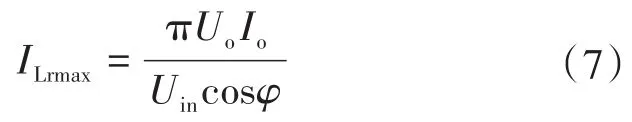
由式（6）可得t=0時刻諧振電流為

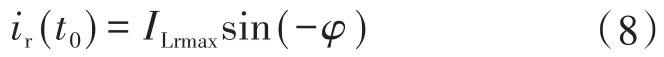
聯立式（5）～式（8）得到滿足軟開關的阻抗角為

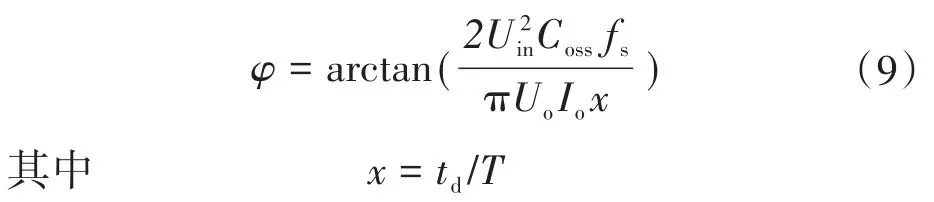
式中：x為死區時間與開關周期的比值。

從式（9）可見阻抗角還與負載電流有關。圖4所示為阻抗角與負載電流的關系，當負載電流減小時，阻抗角將增大，在空載時，阻抗角將接近于90°。負載電流最大時，對應的阻抗角最小，因此設計時應按最大負載電流計算所需的阻抗角。圖5所示為實現零電壓開通所需的最小阻抗角與死區時間的關系曲線，可以看到，死區時間越大，其所需的阻抗角將越小，這有利于減小損耗。但同時也可以看到死區時間與阻抗角之間并不是線性關系，當死區時間大于一定值時，曲線將變得平緩，阻抗角隨死區時間的變化將不明顯。

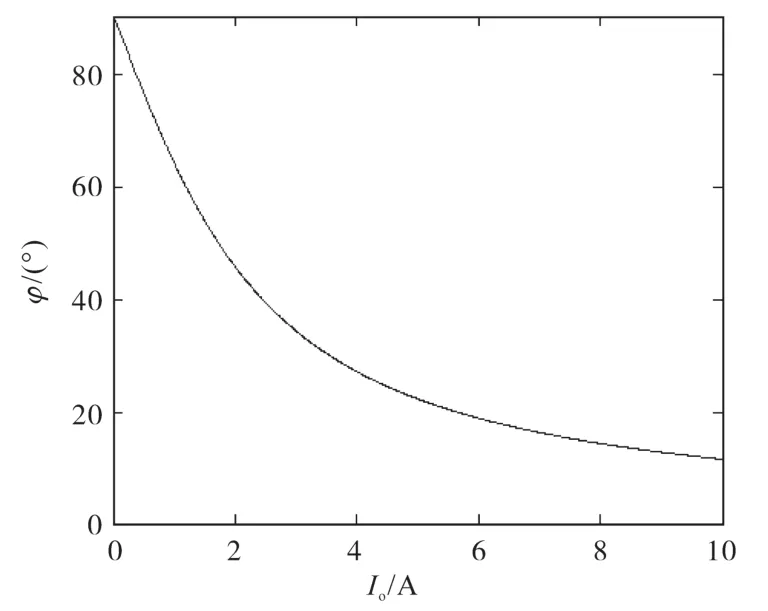
圖4 阻抗角與負載電流的關系Fig.4 Relationship between impedance angle and load current

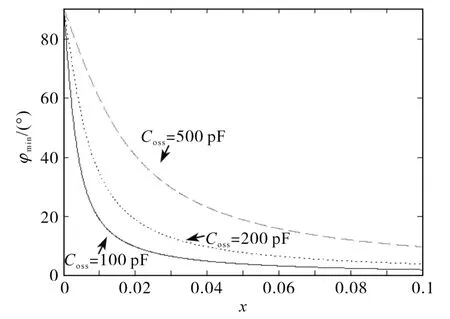
圖5 最小阻抗角與死區時間的關系曲線Fig.5 Relastionship between minimum impedance angle and dead time

2.3 死區時間對變換器的影響

雖然增大死區時間將減小損耗，但是增大死區時間，使得開關管的占空比減小，將影響諧振電流。由于在開關管導通期間，輸入諧振網絡的有功功率為

因此諧振電流有效值為

由式（11）可得到歸一化的諧振電流如下式：

式中：Iin為輸入電流有效值；ω為諧振頻率。

圖6所示為死區時間、阻抗角和諧振電流之間的關系曲線。從圖中可以看到，當阻抗角達到一定值時，諧振電流將急劇增加，這與圖3所示一致。死區時間越小，歸一化諧振電流越接近1，諧振電流越小，使得導通性損耗也越小。但是由于死區時間越小，軟開關所需要的諧振阻抗角越大，因此需要折中選擇死區時間和諧振阻抗角。從圖3和圖6可見，阻抗角小于20°時，阻抗角的變化對損耗和諧振電流的影響非常小。因此可以將阻抗角設定在小于20°的范圍內，再根據軟開關條件選擇死區時間。

圖6 死區時間、阻抗角與諧振電流的關系曲線Fig.6 Relationship between deadtime，impedance angle and resonant current

3 LCC諧振變換器諧振網絡參數設計

從前述分析可以看到，LCC諧振變換器參數設計時，不僅要滿足軟開關條件，還需要使得諧振阻抗角在合理范圍，才能使得諧振網絡無功環流最小，變換器的導通損耗最小。因此LCC諧振變換器諧振網絡參數設計應該首先考慮死區時間與滿載時諧振阻抗角的選擇，然后再根據輸出的電壓電流確定變壓器匝比及諧振網絡參數。具體的參數設計步驟如下：

1）死區時間的選取。LCC諧振變換器的死區時間對諧振網絡阻抗角和變換器效率有重要影響，因此要實現諧振網絡參數的優化設計，首先需要合理選取死區時間。而死區時間與開關管的輸出寄生電容密切相關，可以根據所選的開關管的輸出寄生電容，由式（9）得到死區時間為

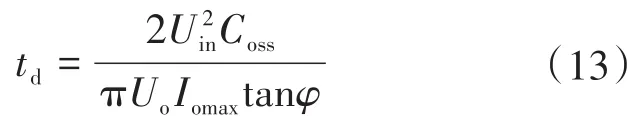
式中：Iomax為最大負載電流。

阻抗角φ可以根據圖5選擇，一般小于20°。

2）變壓器匝數比的確定[9]。從圖2所示的波形可以看到，在t2—t5時間段內，變壓器副邊二極管導通，原邊向副邊傳遞能量，因此輸出電流平均值為

可得變壓器的匝數比為

3）導通角的取值。從工作狀態可知，在t1—t2階段，諧振電流給并聯電容Cp充電，使得Cp兩端的電壓從-nUo變到nUo，因此有：

從圖2的波形可以看出，導通角為半個開關周期減去電容電壓上升的時間，因此有：

4）諧振網絡參數的確定。由式（17）可以得到LCC諧振網絡的并聯諧振電容為

定義k為電容比，即k=Cp/Cs，當k值越大，其特性越接近并聯諧振，LCC諧振變換器的頻率范圍越窄，一般情況下為簡化分析取k=1。由此可得串聯諧振電感為

由以上可以完成整個諧振網絡參數的設計。

4 實驗結果

采用本文提出的方法設計了160 W LCC諧振變換器，主開關管采用IPB60R060P7，從規格書上可以得到該MOSFET輸出等效電容為89 pF，根據圖5、圖6，選擇死區時間為開關周期的1%，即160 ns，阻抗角設置為18°，關鍵參數及元件值如下：輸入電壓Uin=400 V，輸出電壓Uo=80 V，滿載輸出電流Io=2 A，滿載開關頻率fs=60 kHz，變壓器匝數比n=3，諧振電感Lr=700 μH，串聯諧振電容Cs=10 nF，并聯諧振電容Cp=10 nF。

圖7所示為LCC諧振變換器的實驗波形，波形中Ug1，Ug2分別為半橋開關管Q1，Q2的驅動信號，Ua為半橋中點電壓，即下管Q2的漏源極電壓波形，ir為諧振電流波形。圖7a為變換器滿載時的波形，圖中可見諧振電流ir滯后于半橋中點電壓Ua，滯后時間為0.8 μs，由于開關頻率為60 kHz，因此阻抗角為18°。從圖7的波形可以看到，隨著負載的減小，諧振網絡的阻抗角逐漸增大，當空載時，從圖7e中可以看到電流滯后于電壓90°，與前面分析一致，變換器諧振網絡中有大量無功功率，空載時的諧振電流最大值仍然接近0.6 A，這使得變換器雖然更加容易實現軟開關，但是由于無功環流較大，LCC諧振變換器空載損耗較大。在圖8所示的變換器效率曲線中可以看到，由于輕載時的無功環流較大，因此變換器在輕載時效率較低，滿載時效率可以達到94.2%。

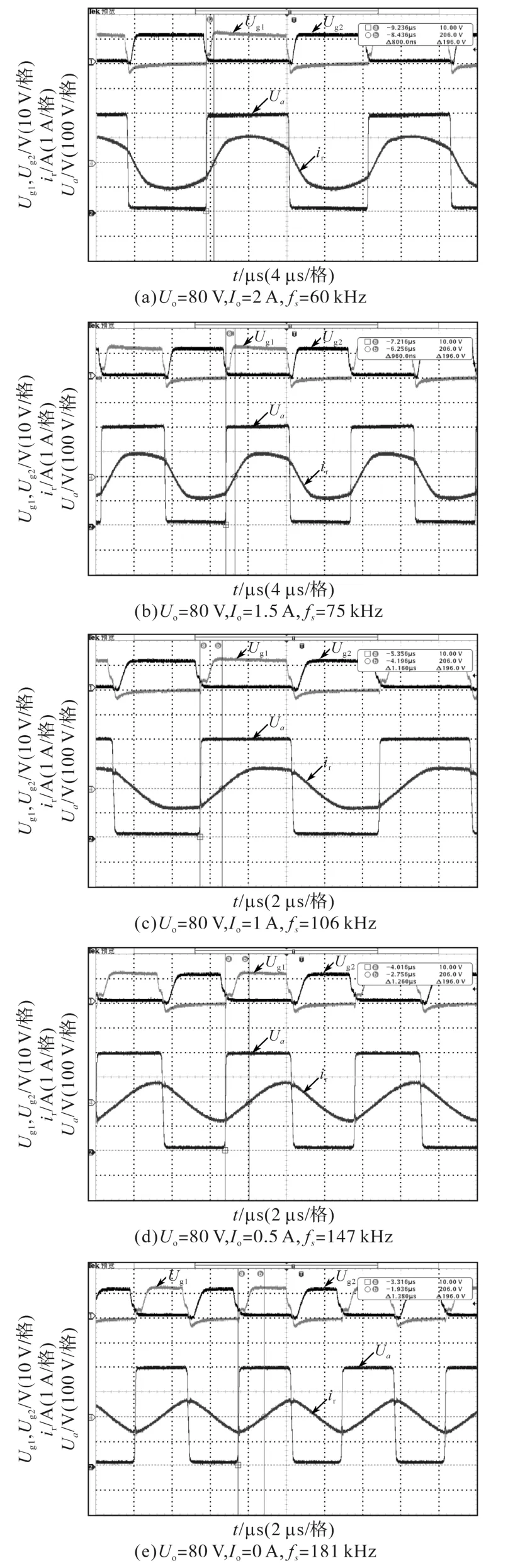
圖7 LCC諧振變換器的實驗波形Fig.7 Experiment waveforms of LCC resonant converter

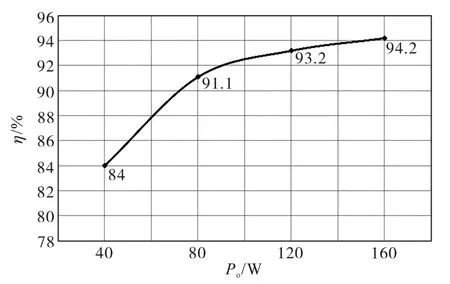
圖8 LCC諧振變換器的效率曲線Fig.8 Efficiency curve of LCC resonant converter

5 結論

由于諧振阻抗角及死區時間對LCC諧振變換器的損耗有重要影響，因此需要對LCC諧振變換器的阻抗角和死區時間進行研究。通過分析LCC諧振變換器死區時間、諧振阻抗角和效率之間的關系，提出在滿足軟開關條件下的諧振阻抗角和死區時間選擇方法，并以此為基礎提出了LCC諧振變換器的參數設計方法。實驗證明本文提出的方法可行，提高了變換器效率。本文提出的設計方法對各種應用場合的LCC諧振變換器的設計都具有借鑒意義。