考慮分布式可再生能源的通證激勵機制設計與分散式電力市場研究

白昱陽，張俊，王曉輝，陳思遠，高天露，劉鵬

(1.武漢大學電氣與自動化學院，武漢市 430072；2. 中國電力科學研究院有限公司，北京市 100192)

0 引 言

隨著全球化石能源的緊缺和環境污染加劇，加強環境保護、轉變電能生產方式、開發可持續的清潔電能成為了世界各國的共識。以風能、太陽能等為主的可再生能源由于其儲量大、無污染的特性，對于緩解能源緊缺、優化能源結構有著十分重要的作用[1]。

近些年，世界各國紛紛加大了對可再生能源發電的發展力度[2]，風能、太陽能等可再生能源的發電技術日益成熟，各國的風電或光伏發電的裝機容量逐年提升。然而，由于可再生能源發電的隨機性和波動性，可再生能源的并網率始終處于較低水平，大規模的棄風棄光現象亟需利用有效的技術手段解決。現階段，單獨依靠源側的靈活性機組很難實現可再生能源的高比例消納，還需要利用市場的手段，結合需求側進行資源的聯合優化配置，促進可再生能源在電力市場中進行消納[3-6]。

分布式可再生能源作為可靈活配置的資源，在參與電力市場時會以大規模分散式主體的形式存在，這給集中式的電力市場出清帶來了極大的挑戰。因此，考慮到分散式市場主體的交易規模和隱私保護等因素，研究適合于包含大規模分散式主體的分散式電力市場模式具有重大意義。文獻[7]分析了英國電力零售市場的改革與挑戰，其通過分散式電力零售市場交易機制與監督體系促進電力零售市場的自由化。文獻[8]對北歐電力市場進行了研究與分析，其利用分散式電力市場機制形成了首個跨國分散式電力交易市場，在可再生能源消納、智能電網建設等方面取得了較好效果。

然而，可再生能源發電具有極大的隨機性和波動性，會導致其參與到電力市場時無法與傳統火力發電進行競爭。因此，需要設計合適的市場機制來促進可再生能源參與電力市場。文獻[9]通過對國外電力市場配額制的研究，提出需要針對可再生能源配額制構建適合中國電力市場的市場交易體系，將用戶納入到可再生能源配額中，激發用戶側的靈活性資源幫助實現可再生能源的發展。文獻[10]對國外的可再生能源配額制的研究情況進行了綜述，分析了可再生能源配額制的實施框架及配額制對市場行為的影響，表明配額制可以促進可再生能源的消納。文獻[11]研究可再生能源發電參與電力市場時考慮了碳排放權交易的火電發電商、可再生能源發電商及政府的行為，說明了固定電價和綠色證書交易政策可以提高可再生能源發電的比例。文獻[12]提出了結合可再生能源固定電價制和綠色證書配額制的發電商決策分析模型，此模型以市場所有發電商的總體利益最大化為目標，并采用多智能體粒子群算法進行求解，驗證了所提市場優化模型的有效性，能夠有效地促進可再生能源的發展。

可再生能源配額制能夠很好地促進可再生能源的發展，然而可再生能源配額制主要存在以下局限性：1)可再生能源的配額是未來能源結構的發展目標，現階段缺乏有效的激勵手段[13]； 2)可再生能源配額制是政府強制要求可再生能源占比的一種模式，缺乏完全市場化的激勵機制，市場主體參與促進可再生能源發展的積極性并不能得到有效的保證；3)市場中存在的可再生能源主體主要以大規模分散式的形式存在，這給可再生能源配額制的管控帶來了挑戰。

在此基礎上，本文提出一種基于通證激勵機制的分散式電力市場，以完全去中心化的方式進行分散式電力市場出清，且利用市場化的手段對可再生能源參與市場進行激勵。首先對通證激勵機制和分散式電力市場基本結構進行概述；然后建立以市場發電成本和碳排放治理成本最小為目標、考慮可再生能源參與的分散式電力市場出清模型；接著設計可再生能源發電-通證兌換機制，并建立考慮電價不確定性的含可再生能源發電商行為決策模型；最后進行算例仿真，驗證所提分散式電力市場出清模型和通證激勵機制的有效性。

1 考慮通證交易的分散式電力市場架構設計

1.1 通證激勵機制

考慮到可再生能源具有不可調度性，單一的可再生能源發電機組難以參與電力市場，在激勵機制不足的情況下發電商不愿意承擔偏差費用帶來的利潤風險。傳統的激勵機制均存在一定程度的激勵不足問題，例如碳排放市場中的碳價對發電商的利潤影響太小，利用可再生能源獲得的利潤可能無法覆蓋其出力隨機性帶來的懲罰費用，這是因為碳價作為強化物不具備較大的強化作用。

相比于傳統激勵機制中的強化物，基于通證激勵機制的通證作為強化物會具有很多獨特的優勢[14]，主要表現在以下2個方面：

1)通證一般不受激勵的短暫性狀態影響，其價值不會隨著單一權益的價值波動而波動，可以持續具有較強的激勵作用；

2)通證一般選用具有安全、高效、流通速度快的物品，可以促使市場中各種利益主體進行交易，避免了傳統激勵機制只對部分主體具有激勵機制的局限性。

考慮到電力系統有著節能減排和維持系統穩定的目的與需求，在本文中主要考慮對發電商使用可再生能源的激勵機制。市場運營中心通過計算發電商使用可再生能源發電而減少的碳排放量，按照一定的折算率建立可再生能源發電量與通證獎勵量的獎勵關系，在發電商獲得通證后允許其使用通證在市場中兌換市場競爭權益(例如電量市場的優先出清電量、調頻市場的調頻準入量等)，由于所對應的權益是與市場相關的收益，在不給市場造成額外的財政補貼壓力的情況下最大化發電商的可能利潤。

1.2 市場架構

本文所提的分散式電力市場由電量市場和通證市場兩大部分組成，其結構如圖1所示。電量市場是以分散式方式進行出清，各發電商通過信息交互的方式進行迭代共識與信息更新，在不依賴于市場中心協調機構的前提下形成市場的出清方案。通證市場是以掛牌成交、點對點交易的方式運行，發電商在市場運營中心掛出愿意出售的通證數量，通證的價格是根據通證市場中掛牌交易的情況而決定的，交易雙方通過雙向報價和協商撮合的方式來形成通證的交易價格。

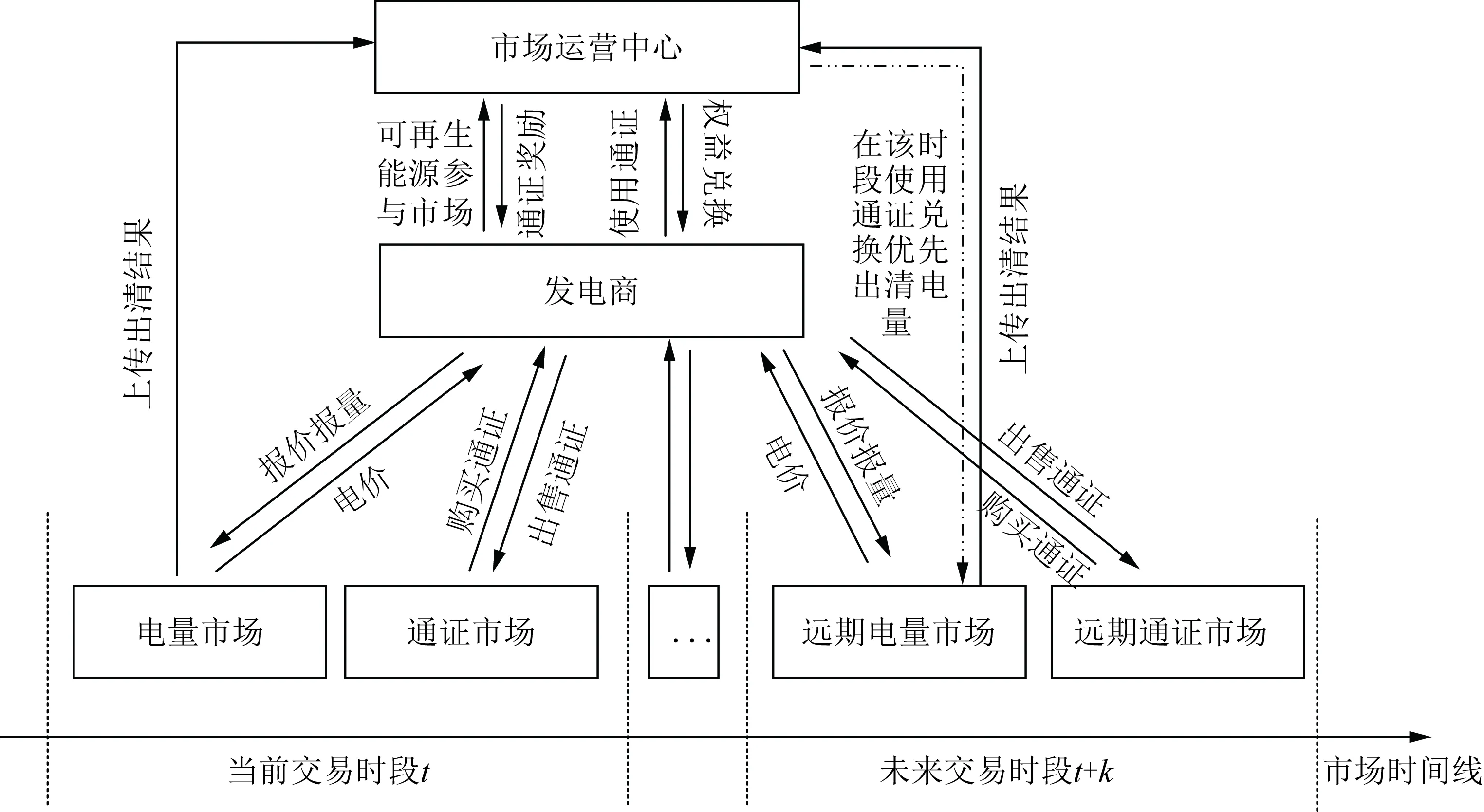
圖1 分散式電力市場運行結構圖Fig.1 Diagram of the operation structure of distributed power market

如1.1節中所述，通證可以用于電量市場兌換優先出清電量，使用可再生能源的發電商會被獎勵一定數量的通證，通證市場設置在電量市場之后用于市場各主體間進行通證交易。因為通證的權益、價格與市場電價有著一定的關系，且隨著市場中通證的數量而改變。在通證市場中，發電商會根據遠期電量市場的價格和市場中通證的交易情況來選擇通證出售策略，最后通過點對點交易的方式與市場中購買主體完成交易。

2 含可再生能源的分散式電力市場模型

電力市場出清是一個發電商與用戶的雙邊決策問題，對電力市場的均衡有著重要的意義。在電力市場的出清計算時必須滿足電力系統的約束條件，如功率平衡約束、機組自身的出力及爬坡約束等。由于市場的出清電價一般作為市場的結算電價，對于參與電力市場的發電商來說，準確掌握市場的出清電價，則可以按照市場出清電價選擇合理的報價策略，幫助發電商實現自身收益的最大化。本節在分散式電力市場出清的基礎上，引入了可再生能源參與電力市場的激勵機制，利用納什均衡模型對通證市場的實時和遠期市場價格進行出清，最大化通證激勵機制在分散式電力市場中的促進作用。

2.1 分散式電量市場出清模型

2.1.1出清模型構建

在分散式電力市場中，建立基于直流潮流最優的分布式安全約束經濟調度模型，在考慮了電力系統網絡潮流約束的同時，從系統的經濟性、可靠性等功能性目標函數出發對各節點發電資源進行優化調度。同時，由于考慮可再生能源參與市場帶來的影響，在出清模型中將系統的碳排放治理成本作為目標函數之一。因此，含可再生能源的分散式電力市場的出清模型詳述如下。

1)火電機組發電成本。

火電機組的成本即為發電的燃料成本，一般考慮為發電功率的二次函數，發電成本函數為：

(1)

2)可再生能源機組運行成本。

可再生能源機組運行成本考慮為發電功率的一次函數，運行成本函數為：

(2)

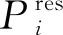
在本節考慮的是可再生能源和火電按比例上網的策略，假定可再生能源和火電的占比分別為σi和1-σi，且0≤σi≤1。

則可再生能源機組和火電機組出力分別為：

(3)

(4)

(5)

式中：Pi為發電商i的出力值。則發電商成本函數為：

Ci=ai[(1-σi)Pi]2+bi(1-σi)Pi+

(6)

3)碳排放成本。

由于可再生能源發電具有無污染的特點，幾乎不產生對環境有害的氣體，因此系統中增加可再生能源發電可以減少電力系統的碳排放，降低環境治理成本。含有可再生能源發電和火力發電的發電商i由于碳排放產生的環境治理成本為：

(7)

式中：φres和φT分別為單位可再生能源機組和火電機組出力產生的碳排放量；k0是單位碳排放量的治理成本系數。

根據式(1)—(7)，系統的總成本為：

(8)

式中:Ωb為電網中所有節點的集合。

4)約束條件。

(1)功率平衡約束：

(9)

式中：PLi為電網節點i的負荷總量；θi和θj分別為電網節點i和節點j的電壓相角；Bij為電網節點i和節點j之間線路的電納值；Ωi為與節點i相連的電網節點的集合。

(2)線路功率約束：

(10)

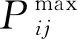
(3)發電機組功率約束：

(11)

(12)

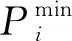
2.1.2出清模型求解

根據共識-新息(consensus innovations approach, CIA)算法[15]的迭代形式，將拉格朗日函數L對拉格朗日乘子λ和θ的一階偏導作為算法的梯度尋優方向，利用電網節點之間的信息交互，對節點信息進行分布式更新，最終迭代收斂到一個全局的最優解[16]。

拉格朗日乘子λ作為電網潮流平衡約束的影子價格，為系統節點間進行交互的信息之一，根據其一階偏導最優性可作為電網節點的出清電價，在不考慮阻塞成本時，不同節點間的λ值最終會收斂到一個值，即為系統統一出清電價。系統出清模型的一階最優性條件推導見附錄A，因此可以利用節點間的交互信息對λ和θ進行更新，電網節點i的λ值更新過程如式(13)所示：

(13)

式中：k為迭代次數；α、β為迭代更新參數。

拉格朗日乘子θ也為節點間交互的信息，其根據拉格朗日函數對λ的偏導進行更新電網節點i的θ值，迭代更新過程如式(14)所示：

(14)

式中：γ為迭代更新參數。

在拉格朗日乘子λ和θ更新之后，對本地發電功率進行更新，在分散式電力市場中，表現為電網節點的發電商不斷依據周圍電網節點發電商的報量信息，不斷調整自身的功率報量的過程，電網節點i發電商的功率更新公式如式(15)所示：

Pi(k+1)=

(15)

(16)

(17)

式中：δ為迭代更新參數。

以上的共識-新息算法通過各節點之間的信息交互和共識以分布式的方式完成。系統中各節點會與鄰域節點交換并共識節點的電價與相角等數據，并根據鄰域節點的數據更新自身的功率值，最終形成全網統一出清邊際電價。

2.2 通證市場出清模型

在本節中，將獎勵通證和可再生能源發電對應起來，建立通證市場，將通證對應的價值在市場中進行流通。通證市場在電力市場出清后進行交易，并不考慮發電商使用通證兌換其他權益獲得的遠期不確定收益，僅考慮發電商在通證市場中售出所持有的通證獲得的收益。當發電商采用可再生能源發電時，根據其可再生能源出力通過一定的兌換率獲取通證，如式(18)所示：

(18)

式中：Qi表示發電商i兌換獲得的通證數量；ρ表示可再生能源出力-通證兌換率。

基于古諾均衡模型[17]的基本假設，建立通證市場的通證價格模型。因此，通證的市場出清價格和通證數量可以描述為如下的逆價格需求函數關系：

(19)

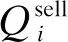
由于通證具有可流通和可持有的雙重屬性，發電商在獲得通證后可以自行決定是否立即進行交易或者將其保留下來以便在未來進行通證交易時可獲得更大的收益。參照電力市場的市場分類，將通證市場分為現貨通證市場和遠期通證市場，因此需要分別對現貨通證市場和遠期通證市場建立相應的通證價格模型。

1)現貨通證市場通證價格模型。

現貨市場的均衡出清比較直觀，通過現貨市場中存在的通證交易總量，可以求出均衡情況下的通證價格，現貨市場通證價格-數量關系如圖2所示。

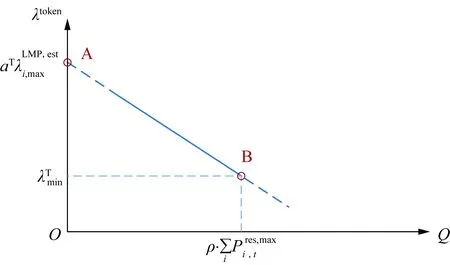
圖2 現貨市場通證價格-數量關系圖Fig.2 Relationship between token price and quantity in the spot market

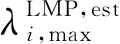
因此，現貨市場基于古諾模型的通證價格模型的系數可以表示為：

(20)

(21)

2)遠期通證市場通證價格模型。

在古諾模型的基本假設中，數量和價格成逆需求關系，對遠期通證市場建立通證價格模型需要通過對遠期的最大通證總數進行估計，即為系統接下來時刻所有市場參與者獲得最大通證數量且均保留通證至遠期交易的情況，本文考慮為系統此后的總負荷需求對應的通證數量。遠期市場通證價格-數量關系如圖3所示。

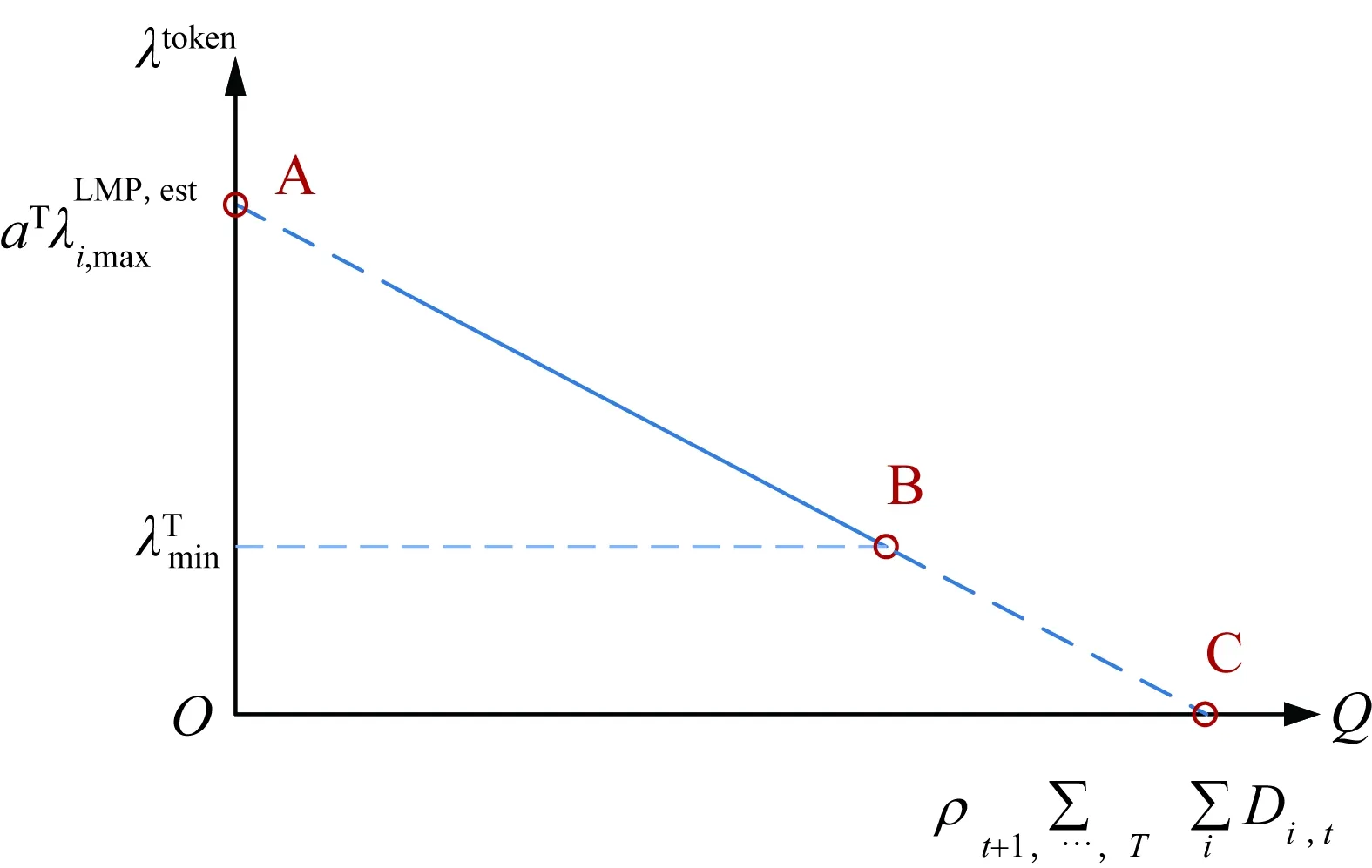
圖3 遠期市場通證價格-數量關系圖Fig.3 Relationship between token price andquantity in the forward market

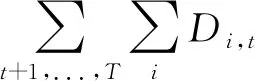
(22)

(23)

3 通證激勵機制下含可再生能源的發電商決策模型

3.1 決策模型構建

考慮到通證的激勵機制，發電商將會考慮在電力市場更多地采用可再生能源機組發電，以此兌換一定的通證從而在通證市場中獲利。然而，由于可再生能源發電的隨機性和波動性，較多地采用可再生能源發電可能帶來較大的發電偏差懲罰費用，因此市場中的發電商會利用市場出清情況對自身發電策略進行最優決策。為了驗證本文所設計的基于通證的激勵機制的有效性，通過對發電商的行為決策建模來分析發電商在激勵機制下的決策行為，以電力市場中的發電商為研究對象，建立發電商在電力市場和聯合市場的聯合決策模型。

(24)

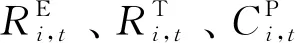
3.2 不確定性建模

3.2.1可再生能源出力的不確定性處理

由于可再生能源的隨機性和波動性，發電商的實際發電量可能和電量市場中出清電量存在偏差，導致市場偏差考核時為發電商帶來懲罰費用，因此在發電商決策分析時需要考慮可再生能源發電的不確定性，本節對可再生能源的不確定性采用場景化的處理方式進行處理。

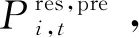
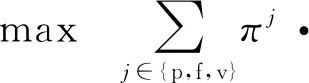
(25)

3.2.2基于IGDT的電價不確定性處理

對單一發電商進行行為決策分析時，由于各個發電商決策的出力波動以及市場用電的變化可能會導致日前市場統一出清電價(market clearing price, MCP)發生改變。針對單一發電商，考慮電價的不確定性因素，對電價的不確定性進行建模，以求得發電商在電價波動時的魯棒收益，作為發電商決策的依據。

信息差距決策理論(information gap decision theory, IGDT)方法[18]可在概率密度函數缺失的情況下處理不確定參數，不失一般性，針對最小化問題，IGDT的模型可表達為如下形式：

(26)

式中：X為決策變量；?為不確定參數；Hi(·)和Gi(·)為變量滿足的不等式約束和等式約束函數；Φineq、Φeq分別為不等式約束和等式約束函數編號集合；Γ為?的取值集合。且不確定參數?的數學表達式可表述為：

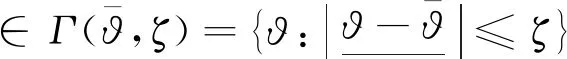
(27)

(28)

式中：fb為目標函數基準值。IGDT的主要目的是幫助決策者適當調整決策變量，以避免由于不可控參數的不確定性使系統無法達到最低要求的風險。

本節將統一出清電價作為IGDT模型中的不確定參數，通過IGDT方法輔助發電商進行魯棒性決策。并引入正參數ε，來描述決策者對于參數不確定性導致目標函數惡化的容忍程度。顯然在ε給定的前提下，最優的魯棒決策可以使系統容忍不確定參數最大程度波動，基于上述思想，式(28)可轉化為式(29)：

(29)

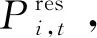
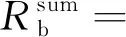
(30)

則本文在考慮電價不確定性時的發電商決策模型可描述為：

(31)

綜上所述，基于本節的不確定性建模方式，式(24)構成了本節考慮可再生能源出力不確定性造成的偏差懲罰的發電商決策模型，式(24)—(25)、式(30)、(31)構成了考慮電價不確定性的發電商決策模型。

4 算例分析

4.1 算例描述

本節在修改后的IEEE-9節點算例上進行仿真驗證，電網的拓撲如圖4所示。其中在節點1和節點2上分別接入了風電機組和光伏機組，風電數據和光伏數據來源于某實際風電場和光伏電站的實際出力數據，風電和光伏的預測功率出力曲線如圖5所示，電網中節點1、2、3、5和7為5個發電商的接入點，分別記作發電商1—發電商5。發電商2包括了常規火電機組和風電機組，發電商3包括了常規火電機組和光伏發電機組，發電商1、5和7為火電機組，系統中發電機發電數據如表1所示。本文將共識-新息算法中的參數設置為α=0.003/k0.98、β=0.001/k0.001、γ=0.000 5/k0.001和δ=0.005/k0.001，迭代次數設置為1 000次。市場中發電商的可再生能源某時刻預測出力值會影響該時刻自身的中標情況和市場的出清情況。

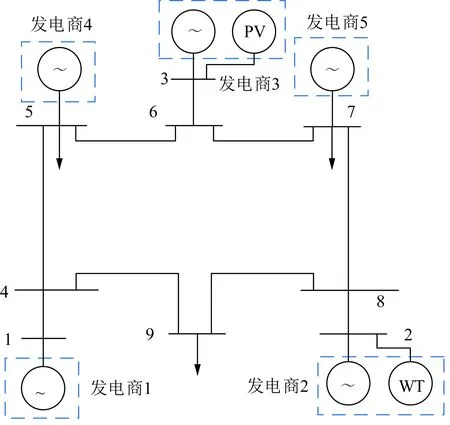
圖4 某地區電網系統拓撲圖Fig.4 Topology of a regional power grid system

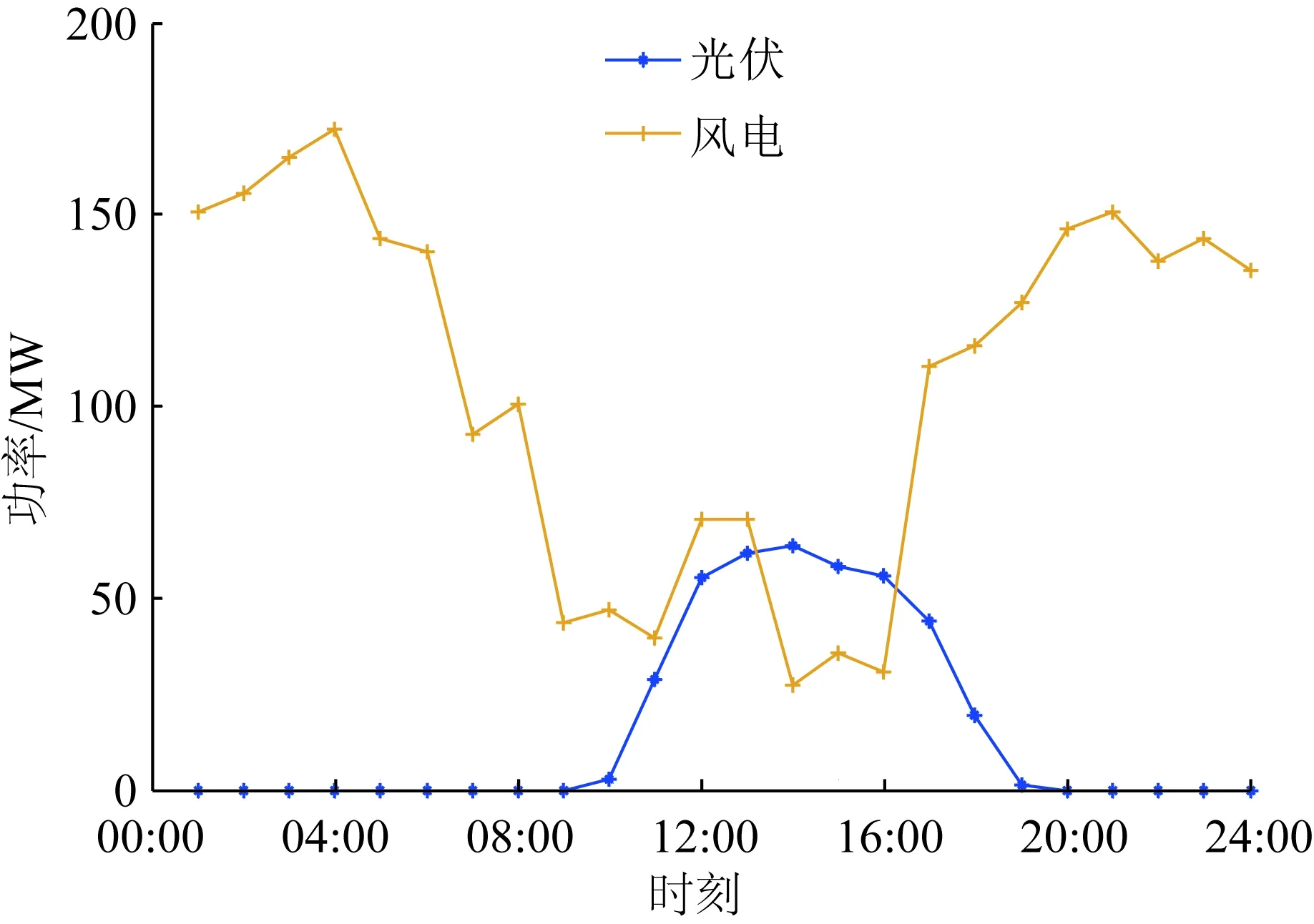
圖5 可再生能源機組功率預測值Fig.5 Power forecast value of renewable energy units

表1 系統中發電資源成本系數Table 1 Cost coefficient of power generation resources in the power system

4.2 分散式電力市場電價出清分析

4.2.1算法有效性分析

1)單時段市場出清求解。

假設市場中風電和光伏的上網比例均為0.4，為了更好地評估算法求解的有效性，選取風電和光伏均有較為可觀出力值的12:00—13:00時段進行單時段市場出清求解。假設該時段的預測值精準，則風電的預測出力為70.40 MW，光伏的預測出力為61.75 MW。在系統節點5、7、9處有負荷需求，該時段的負荷需求分別為PL5=195 MW，PL7=100 MW，PL9=125 MW，市場出清的結果如圖6所示。

圖6 市場出清過程迭代過程圖Fig.6 Iterative process diagram of market clearing

通過圖6(a)可以看出，本文所提算法在600次左右開始趨于收斂，經過1 000次迭代求解，可以得出市場的出清電價為12.54美分/(kW·h)。從圖6(b)中的曲線可以看出，考慮到風電和光伏的經濟性和市場減少碳排放治理成本的目標，擁有風機的發電商2獲得了較多的出清電量，而火電成本系數偏高的發電商3在配合光伏出力之后也獲得了較為理想的出清電量，其余發電商利用火電出力配合系統進行功率平衡調節。5個發電商的出清電量分別79.34、105.24、65.74、86.79和82.89 MW·h。

仿真數據結果表明可再生能源的出力值對市場出清的影響較大，本節在后續仿真中需對可再生能源的上網比例和可用出力值進行影響分析。

2)全時段市場出清。

為了更好地分析可再生能源發電對市場出清的影響，后續對一天24個時段進行市場出清求解。考慮到不同節點的負荷差異性也會對市場出清情況有較大影響，僅假設節點7和節點9上均是固定負荷(即PL7=100 MW，PL9=125 MW)，僅在節點5上設置實時變化的負荷需求，其負荷需求曲線如圖7所示。同樣地，將風電和光伏的上網比例設置為0.4，市場出清得到的市場全時段MCP和系統中發電商的出力情況分別如圖8所示，全時段MCP數據見附錄B表B1。

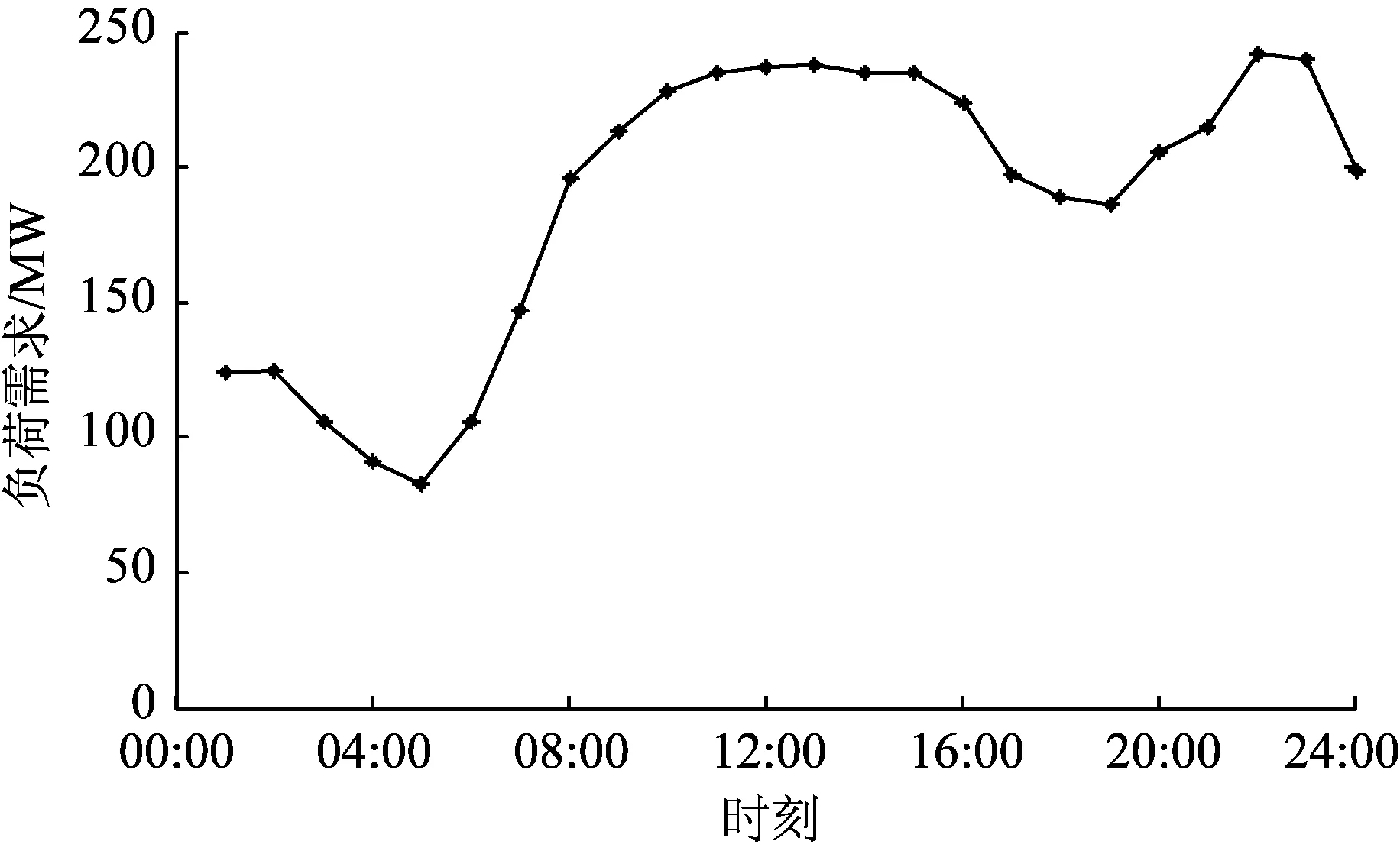
圖7 節點5的負荷需求曲線Fig.7 Load demand curve of node 5

通過對比圖8中(a)和(b)的曲線可以發現，可再生能源參與電力市場可以極大地降低電價水平，而且可以減小電價曲線的波動區間，這是因為風機和光伏可以為系統充當備用電源，當系統負荷波動而火電機組容量不足時，充足的風機和光伏上網供電可以減緩市場的負荷需求沖擊，從而避免出現電價劇烈升高的情況。另外，從圖8(b)中可以看出，當風機可用出力大幅跌落時，電價也會出現小幅增長。在09:00—11:00時段和14:00—16:00時段，風機可用出力下跌導致電價激增，而在12:00—13:00時段光伏可用出力的上漲可以彌補風機可用出力的不足，會導致電價回落。在18:00之后，光伏可用出力為0，風機可用出力逐漸恢復，電價在小幅波動之后又會回落到相對較低的水平。另外，通過對比附錄B表B1中各發電商的發電數據可以看出，含風機的發電商2和含光伏的發電商3總能獲得較多的出清電量，這是因為含可再生能源的發電商具有較低的成本函數，能減少電力系統的總成本。

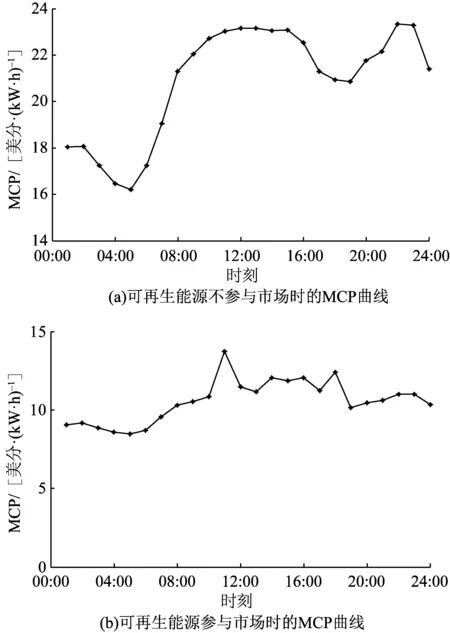
圖8 全時段市場MCP曲線Fig.8 MCP curve of 24 hours

4.2.2可再生能源上網比例對市場出清影響

在上述某地區電網算例中，可以發現可再生能源出力對市場出清得到的MCP有較明顯的影響，但存在可再生能源與火電打捆上網供電時會影響火電靈活性的問題。選取圖5曲線中風電出力最大(在04:00時刻)和光伏出力最大(在13:00時刻)2個場景，調整可再生能源上網比例來分析其對市場統一出清電價的影響，結果如圖9所示。

從圖9中可以看出，在本節理想場景設置下可再生能源上網比例對市場MCP的影響較為直觀，考慮到風電的經濟性優于光伏，風機大規模接入后市場MCP將低于光伏大規模接入時的。因此，在后續的發電商決策分析中，發電商可再生能源與火電的上網比例會

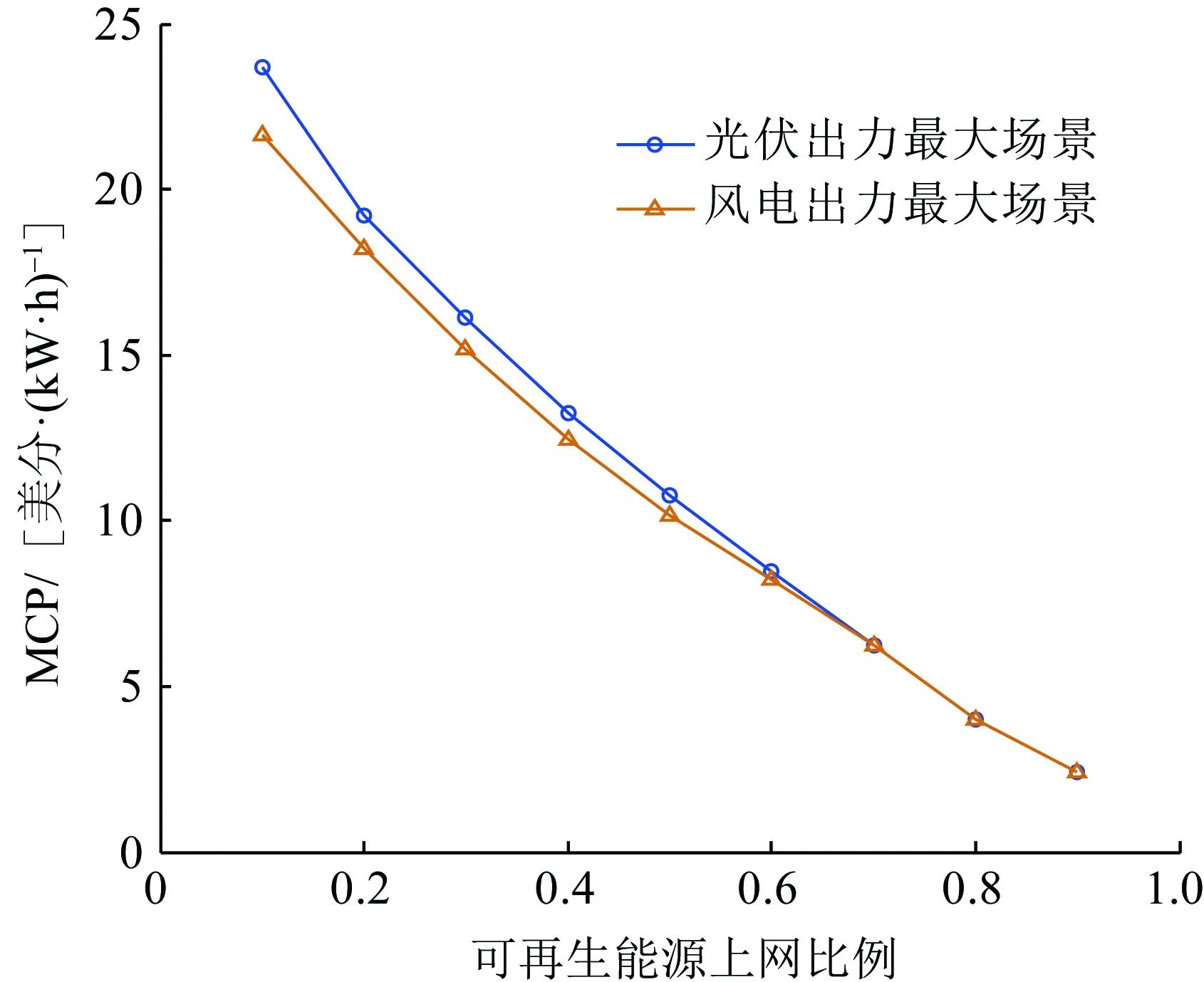
圖9 2種場景下可再生能源上網比例對市場MCP的影響Fig.9 Influence of renewable energy ratio on MCP under two scenarios

對市場實時出清時電價造成影響，在進行發電商利潤分析時應考慮市場MCP的不確定性。

4.2.3算法魯棒性評估

為了驗證本文所采用的共識-新息算法的魯棒性，將算法應用在IEEE-39節點標準算例中進行分布式市場出清，以驗證其在較大的系統中的求解性能，將共識-新息算法中的參數設置為α=0.000 8/k0.98、β=0.000 1/k0.001、γ=0.000 035/k0.001和δ=0.000 1/k0.001。考慮到該方法通過節點之間的信息交互進行迭代與更新，對電力網絡的拓撲變化具有自適應性，設置切機和切負荷2種場景來進行求解分析。在切機的場景中將節點30—33上的4個發電機組切除，而在切負荷的場景中將節點15、16、20上的負荷切除，市場的出清過程如圖10所示。

從圖10中可以看出，切機之后系統電源變少，在市場需求總量不變的情況下需求側競爭較為激烈，導致市場統一出清電價數值變大；相反，切負荷之后系統需求量變少，在電源數量不變的情況下市場出清的統一出清電價數值變小。因此，共識-新息算法可以在系統運行狀況和拓撲結構變化后，迅速收斂到新的市場統一出清電價，從而為分散式電力市場的實時出清提供可靠的保障。

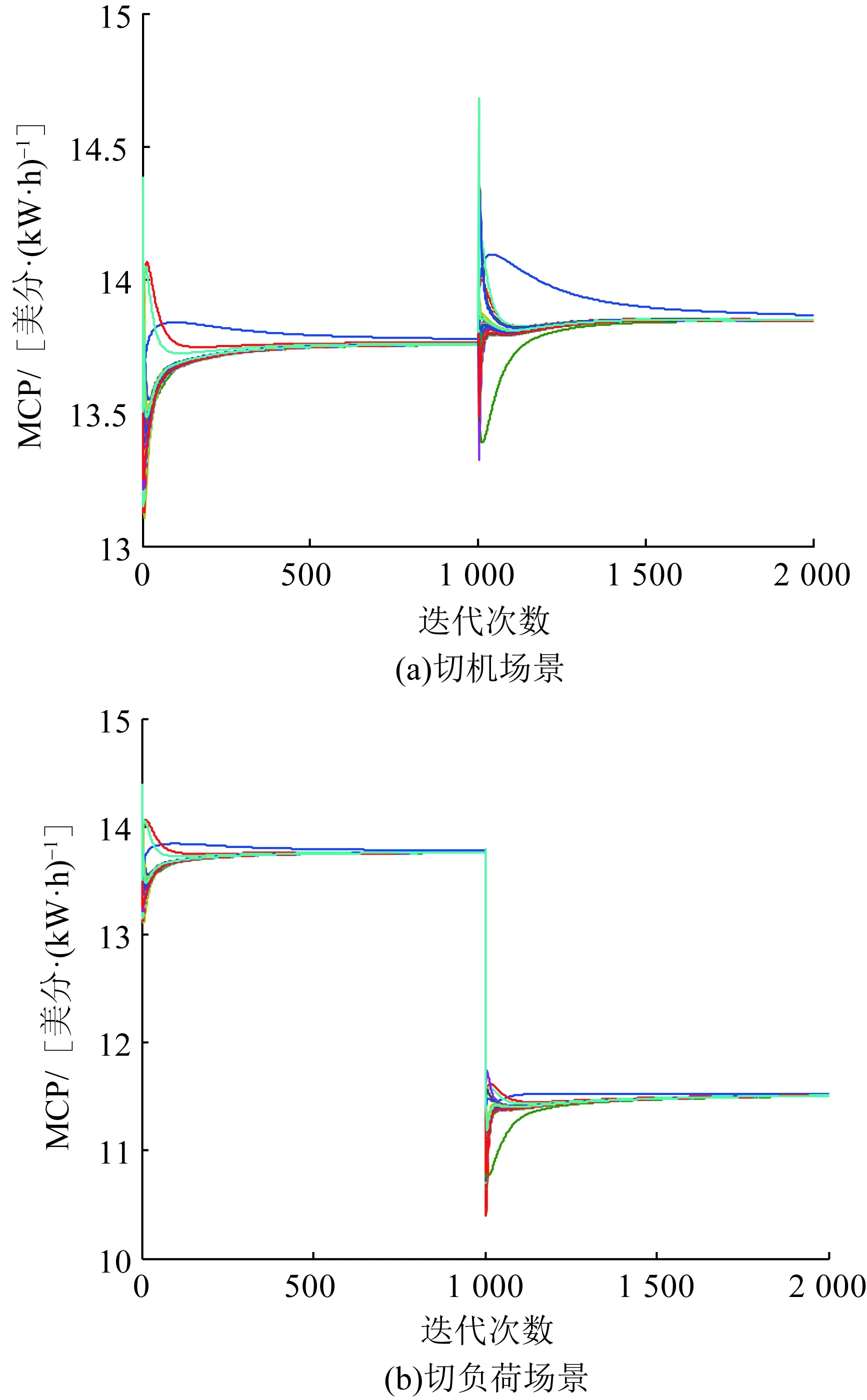
圖10 市場MCP迭代過程變化Fig.10 Iteration diagram of MCP

4.3 含可再生能源的發電商決策分析

4.3.1場景設置

本節在4.2.1節中實際電網系統的仿真結果基礎上進行分析，出清結果選擇可再生能源火電比例為0.4的情況，對系統中的發電商2進行分析，根據仿真結果可知系統24 h的統一出清電價與該發電商的全時段出清量，如附錄表B1所示。仿真依據出力-通證兌換率ρ的不同分為3種情況，對于每種情況，又將其是否引入通證激勵、是否考慮MCP不確定性可分為如下3個場景。

1)場景1：不引入通證激勵，且不考慮MCP不確定性。該場景下發電商出力需滿足日前市場出清的電量，可再生能源出力占比可自我調節，同時針對可再生能源出力的偏差值進行考核。

2)場景2：引入通證激勵，但不考慮MCP不確定性。該場景通過引入現貨和遠期通證市場來激勵發電商提高可再生能源機組出力。

3)場景3：引入通證激勵，且考慮MCP不確定性。發電商需在場景2基礎上進一步進行功率分配的魯棒性決策，以最大程度抑制電價的不確定性。

仿真參數取值如表2所示。

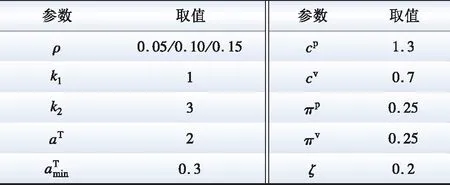
表2 仿真參數取值Table 2 Simulation parameters

4.3.2仿真結果分析

仿真結果基于可再生能源出力-通證兌換率的不同分為如下3種情況。

1)可再生能源出力-通證兌換率ρ=0.05時。

在ρ=0.05時，基于上述數據與參數進行3個場景下的發電商可再生能源機組出力決策與通證市場行為模擬仿真，仿真結果如圖11—13所示。其中圖11為場景1、2下可再生能源與火電24 h出力情況對比；圖12為場景2下現貨/遠期通證價格與發電商通證出售策略；圖13為場景1、2、3下可再生能源出力對比。

圖11 ρ=0.05，場景1、2下可再生能源與火電24 h出力情況Fig.11 Output diagram of renewable energy and thermal generation at 24 hours under Case 1 and Case 2 with ρ=0.05

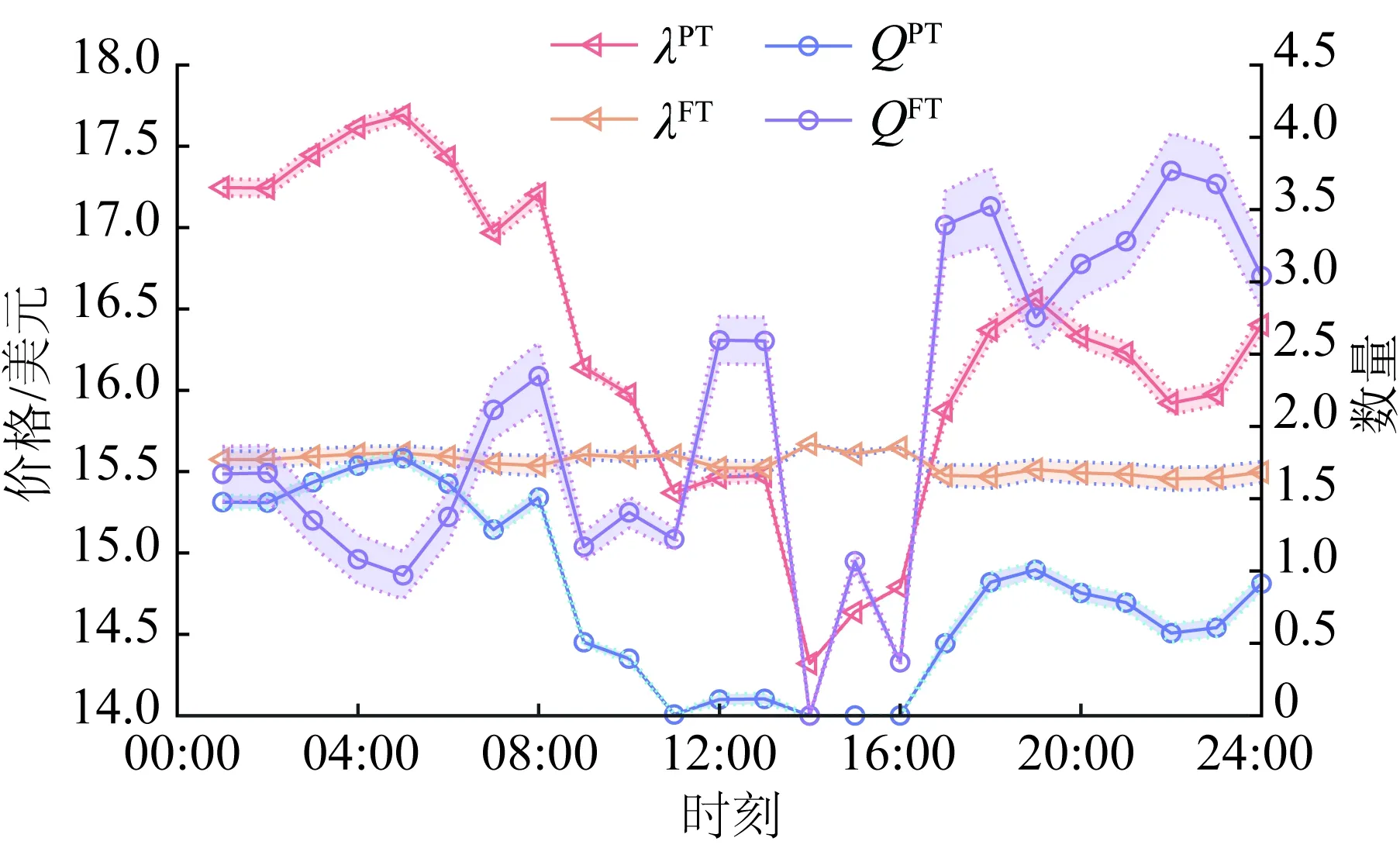
圖12 ρ=0.05，場景2下現貨/遠期通證價格與發電商出售策略Fig.12 Diagram of spot/forward prices and strategies of generators at 24 hours under Case 2 with ρ=0.05

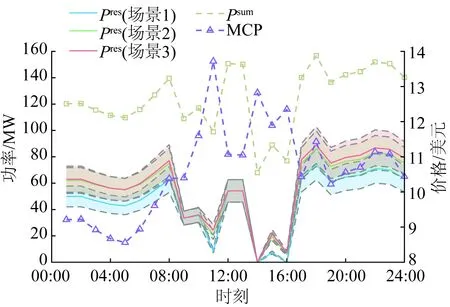
圖13 ρ=0.05，場景1、2、3下可再生能源出力對比Fig.13 Output diagram of renewable energy at 24 hours under Case 1, Case 2 and Case 3 with ρ=0.05

圖11中的陰影區域是由于可再生能源機組的出力不確定性而對應的決策變量范圍。從圖11可以看出，2種場景下的可再生能源出力趨勢總體上均與圖5所示的風電機組功率預測曲線基本保持一致。相比場景1，場景2下發電商的可再生能源出力值得到了大幅提高，且隨著可再生能源出力占比的提高，出力的不確定范圍也逐漸增大，這也對火電機組的調節速度與精度提出了更高的要求。場景1下24 h可再生能源總出力1 124.356 MW·h，而在引入通證激勵后，可再生能源總出力1 347.526 MW·h，出力綜合提升19.856%，證明了通證激勵在引導可再生能源出力方面的有效性。

從圖12可以看出，在價格方面，通證現貨市場波動較大，全時段內價格極差為3.3691 美元；而通證遠期市場則較為穩定，在MCP較高時波動較小，價格極差為0.204 0美元。從通證出售決策方面可以看出，發電商在現貨市場出售的通證數較為穩定，為遠期市場保留的通證數波動更大。綜合上述兩方面信息，可以得出：相比遠期市場，發電商對現貨市場的通證價值估值更高，且當前時段的出力與價格變化對遠期市場的通證價格影響較小，這也與實際市場的運行規律相契合；考慮到現貨市場價格波動大風險高，相比于單次售出所有通證，發電商更傾向在現貨市場售出固定數量的通證獲得基礎收益后，保留大部分的通證用于遠期儲蓄以實現總利潤的最大化，通過計算可知現貨市場售出通證的數量平均占發電商總通證數的29.154%。

由圖13可知，對比場景2、3下的可再生能源出力曲線可以發現，在考慮電價的不確定性后，發電商選擇進一步提高可再生能源機組的出力值以最大化對電價下跌的魯棒性。這是因為相比火電機組可再生能源發電成本更低，故提升可再生能源出力占比能讓發電商在更低的電價下保證期望的收益。綜合3種場景下的可再生能源出力趨勢與負荷曲線和電價曲線可以看出，在電價非高峰時段，可再生能源出力趨勢基本與電價與負荷曲線一致；在電價高峰時期(11：00,14：00,16：00)，可再生能源出力值較低，這是因為雖然可再生能源機組發電成本更低，但考慮到其出力的不確定性而可能帶來的偏差考核懲罰，發電商更傾向在電價峰值時段用傳統機組出力以獲得穩定的最大收益。根據仿真統計數據，場景3下可再生能源總出力為1 386.656 MW·h，相比場景2綜合提升了2.904%。

2)可再生能源出力-通證兌換率ρ=0.10時。

當ρ=0.10時，3種場景的對比仿真結果分別如圖14—16所示。

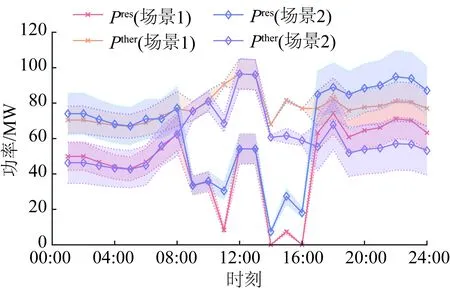
圖14 ρ=0.10，場景1、2下可再生能源與火電24 h出力情況Fig.14 Output diagram of renewable energy and thermal generation at 24 hours under Case 1 and Case 2 with ρ=0.10

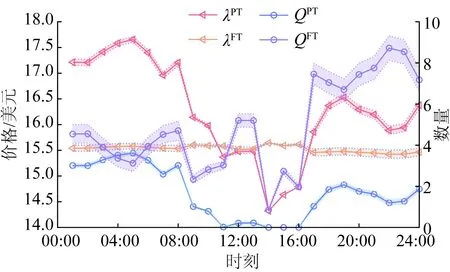
圖15 ρ=0.10，場景2下現貨/遠期通證價格與發電商出售策略Fig.15 Diagram of spot/forward prices and strategies of generators at 24 hours under Case 2 with ρ=0.10

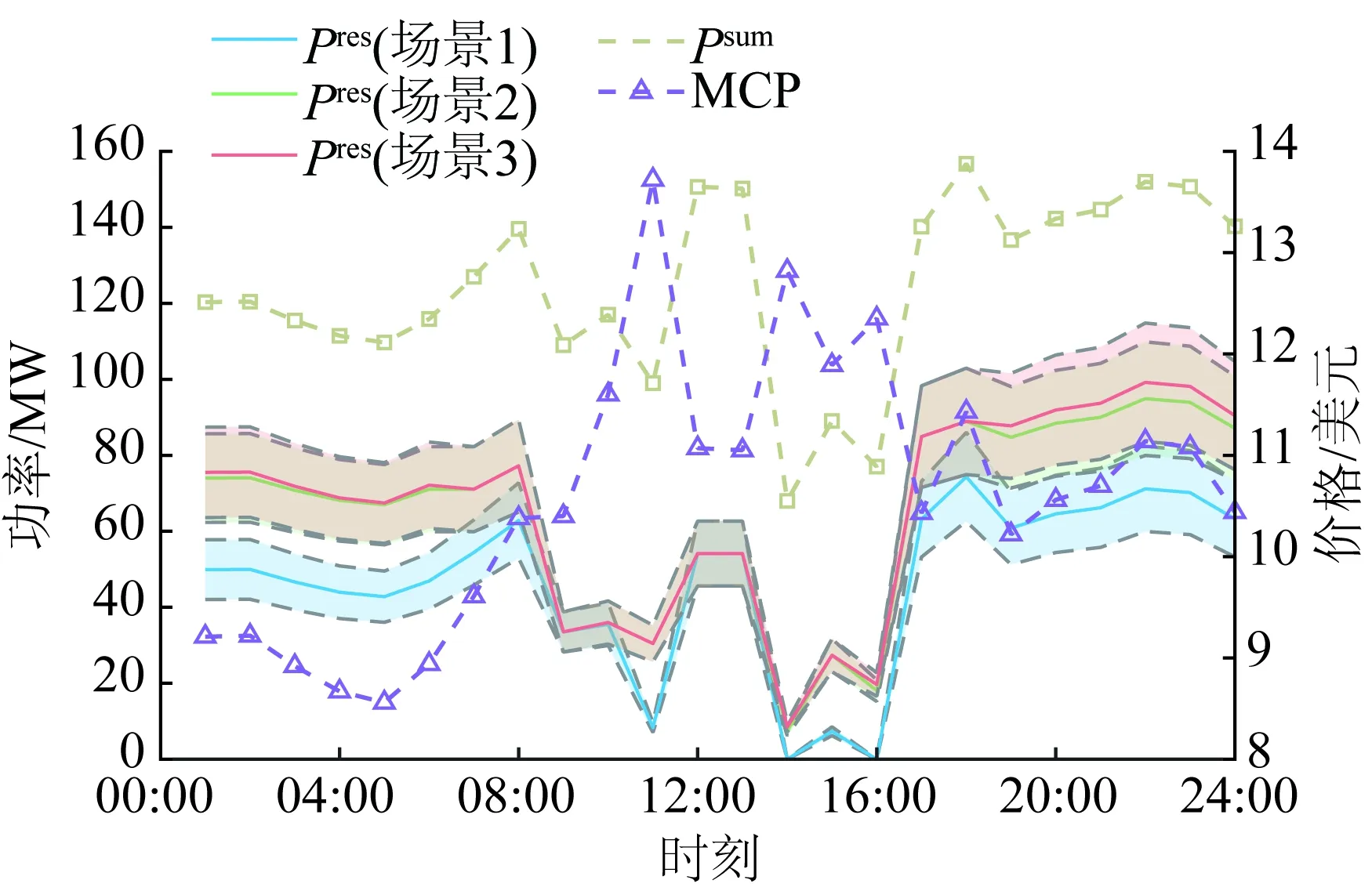
圖16 ρ=0.10，場景1、2、 3下可再生能源出力對比圖Fig.16 Output diagram of renewable energy at 24 hours under Case 1, Case 2 and Case 3 with ρ=0.10

從圖14可以看出，當ρ=0.10時，場景1下24 h可再生能源總出力1 124.356 MW·h，而在引入通證激勵后，可再生能源總出力1 547.383 MW·h，出力綜合提升37.632%。具體分析和ρ=0.05情況類似。

從圖15可以看出，在價格方面，通證現貨市場波動較大，全時段內價格極差為3.336 4美元；而通證遠期市場則較為穩定，在MCP較高時波動較小，價格極差為0.215 1美元。通過計算可知現貨市場售出通證的數量平均占發電商總通證數的25.864%。具體分析和ρ=0.05時類似。

當ρ=0.10時，根據仿真統計數據，場景3下可再生能源總出力為1 578.421 MW·h，相比場景2綜合提升了2.006%。具體分析和ρ=0.05時類似。

3)可再生能源出力-通證兌換率ρ=0.15時。

當ρ=0.15時，3種情況的對比仿真結果分別如圖17—19所示。

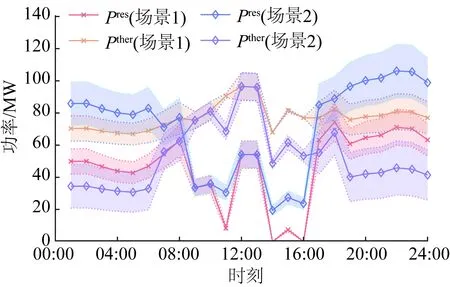
圖17 ρ=0.15，場景1、2下可再生能源與火電24 h出力情況Fig.17 Output diagram of renewable energy and thermal generation at 24 hours under Case 1 and Case 2 with ρ=0.15

從圖17可以看出，當ρ=0.15時，場景1下24 h可再生能源總出力1 124.356 MW·h，而在引入通證激勵后，可再生能源總出力1 706.563 MW·h，出力綜合提升51.790%。具體分析和ρ=0.05時類似。

從圖18可以看出，在價格方面，通證現貨市場波動較大，全時段內價格極差為3.304 1美元；而通證遠期市場則較為穩定，在MCP較高時波動較小，價格極差為0.211 4美元。通過計算可知現貨市場售出通證的數量平均占發電商總通證數的23.83%。具體分析和ρ=0.05時類似。

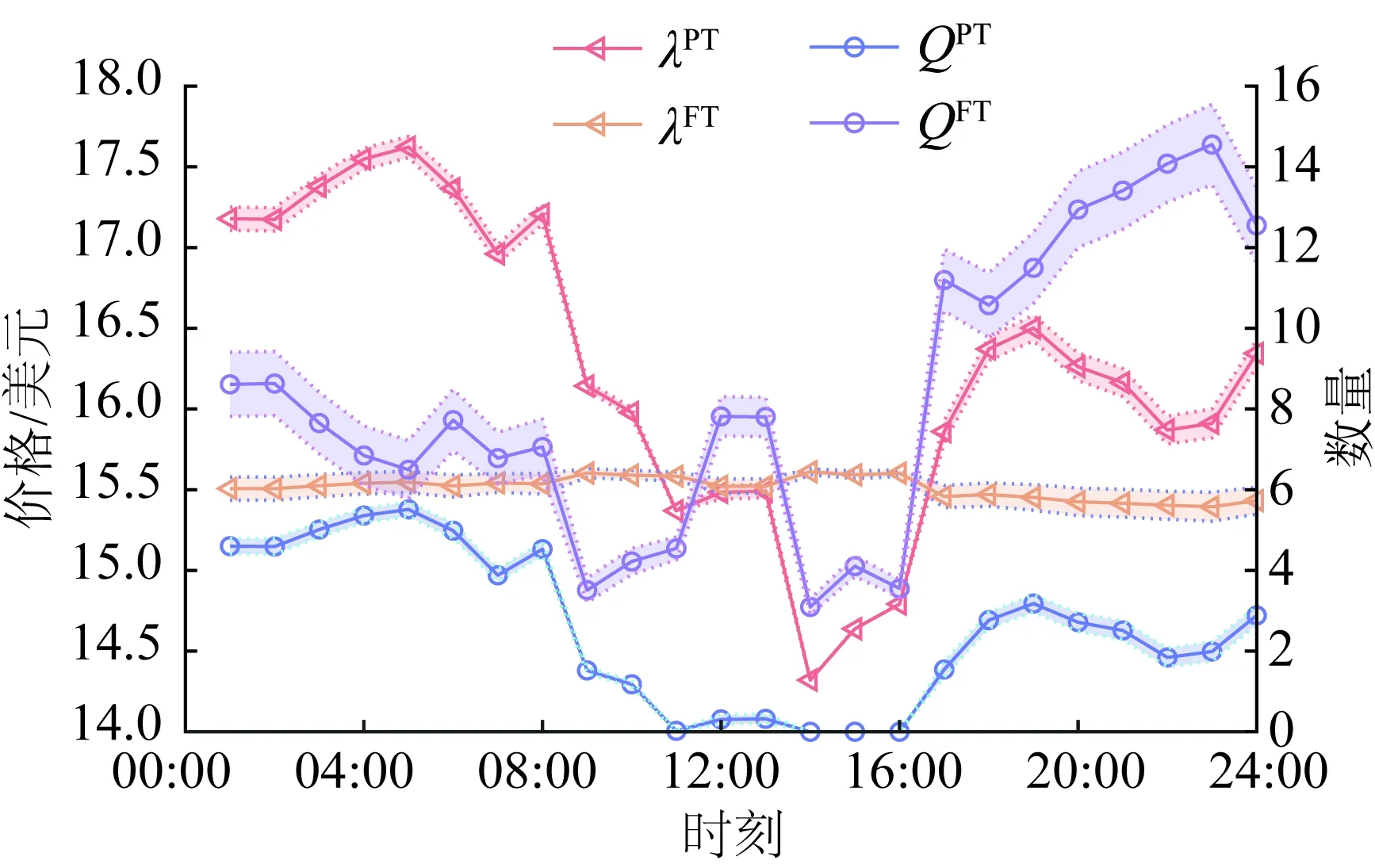
圖18 ρ=0.15，場景2下現貨/遠期通證價格與發電商出售策略Fig.18 The diagram of spot/forward prices and strategies of generators at 24 hours under Case 2 with ρ=0.15

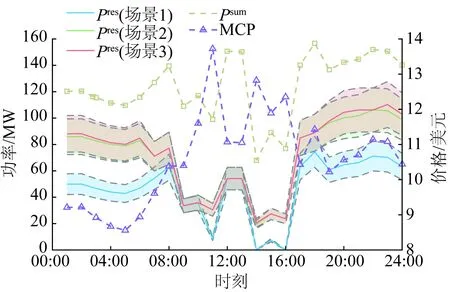
圖19 ρ=0.15，場景1、2、3下可再生能源出力對比圖Fig.19 Output diagram of renewable energy at 24 hours under Case 1, Case 2 and Case 3 with ρ=0.15

當ρ=0.15時，根據仿真統計數據，場景3下可再生能源總出力為1 736.616 MW·h，相比場景2綜合提升了1.761%。具體分析和ρ=0.05時類似。

根據可再生能源-通證兌換率ρ的不同，對3種情況下發電商的決策行為分析詳述如下。

從圖11、14、17可以看出，在不同的可再生能源出力-通證兌換率下，相比不考慮通證激勵的情況，發電商均產生更多的可再生能源出力，說明本文所采用的基于通證的可再生能源發電參與電力市場的激勵機制是有效的，能夠激勵發電商采用更多的可再生能源參與電力市場。考慮不同的可再生能源-通證兌換率，在同一時段進行對比可以看出，隨著兌換率的增加，發電商增加可再生能源出力，因此，在相同的情況下，不同的兌換率對于激勵發電商效果不同。因此在設計基于通證的激勵機制時，需要設置合理的可再生能源出力-通證兌換率，來平衡發電商在聯合市場的收益。

從圖12、15、18可以看出，現貨通證市場和遠期通證市場的價格隨著節點邊際電價的不同而出現波動，發電商決策時都考慮了現貨通證市場和遠期通證市場的博弈情況，沒有將所兌換的通證全部在一個通證市場上進行出售。且隨著可再生能源出力-通證兌換率的提高，發電商在現貨通證市場售出的通證數量逐漸減少。由上面的分析可知，在相同的情況下，發電商受到通證的激勵，決策增加更多的可再生能源出力，因此發電商將獲得更多的通證，考慮到通證市場價格波動的風險發電商也愿意保留通證在遠期市場出售，來平衡自身在通證市場的收益。

從圖13、16、19可以看出，無論何種可再生能源出力-通證兌換率，在考慮電價不確定性時，相比不考慮不確定性的情況，發電商增加了可再生能源的發電量。這是因為在考慮電價最差的情況下，發電商綜合衡量可再生能源出力偏差造成的考核成本，發電商通過增加發電成本較低的可再生能源出力能夠使得發電商的期望收益最大化。當通證兌換率越高時，由于可再生能源出力約束，可再生能源快逼近此時的出力上界值，因此可再生能源出力提升較低。

綜上所述，本文設計的可再生能源通證激勵機制能夠有效激勵含可再生能源的發電商參與電力市場，對于促進可再生能源發展具有重大意義。

5 結 論

隨著可再生能源的消納問題日益突出，可再生能源參與電力市場是促進消納的有效手段之一，含可再生能源的分散式市場模式已成為未來可行的市場構架。本文從電力市場的結構出發，構建了包含電量市場和通證市場的分散式電力市場，以可再生能源和火電“打捆”的方式激勵含可再生能源發電商參與電力市場，建立了含可再生能源的分散式電力市場出清模型，研究并分析了在通證激勵機制下考慮電價不確定性的含可再生能源發電商行為決策問題。在未來的工作中，將會對通證激勵機制在實際電力市場中的應用做進一步地詳細研究。