基于混沌序列與DNA突變原理的彩色圖像加密方案
郝 晉,王 偉,李 慶 宇,曹 穎 鴻
(1.大連工業大學 信息科學與工程學院,遼寧 大連 116034;2.大連工業大學 機械工程與自動化學院,遼寧 大連 116034;3.陸裝沈陽軍代局駐大連地區軍代室,遼寧 大連 116033)
0 引 言
隨著網絡和通信技術的飛速發展,數據的傳輸方式產生了巨大的改變,對數據傳輸安全的要求越來越高。然而,由于數字圖像本身具有的信息量大、相鄰像素點間相關性高的特點,使得常用的加密方法并不能完全滿足數字圖像的加密要求。因此,針對數字圖像加密算法的研究成為研究熱點。由于混沌系統是特定系統中的隨機或不確定運動,具有許多獨特的特性,如遍歷性、內在的隨機性和對初值的敏感性[1-2],使得混沌系統在圖像加密算法的設計中具有廣泛的應用前景[3-6]。
與整數階混沌系統相比,分數階系統能更準確地反映自然現象,這使得分數階混沌系統得到了廣泛的研究。與傳統的分數階系統求解算法相比,Adomian分解法具有收斂速度快、資源消耗少、計算速度快等優點,被廣泛應用于分數階混沌系統的求解。目前,有很多基于ADM算法的分數階系統的研究與應用。Yang等[2]研究了分數階4D憶阻超混沌電路的動力學特性,并將其應用于圖像加密。Zhang等[7]分析了分數階混沌系統的同步和自適應問題。Ayub等[8]研究了分數階反饋控制的動力學問題。Manoj等[9]分析了分數階的動態特性,并將其應用于圖像加密。本研究提出了一種三維分數階簡化統一系統,并對其分數階系統動力學特性進行了分析。
目前,基于混沌系統已經提出了多種圖像加密算法。文獻[10-11]提出了基于離散混沌系統圖像加密算法,文獻[12-14]采用超混沌系統圖像加密算法。為了提高圖像加密算法的安全性能,在圖像加密過程中加入了DNA序列編碼。文獻[15-16]提出了一種新的基于混沌系統和DNA操作的圖像加密算法。文獻[4,17]提出了一種基于DAN計算和混沌系統的新型圖像加密算法。本研究將DNA突變理論引入到加密算法中,以期進一步提高圖像加密算法的安全性,降低密文圖像與明文圖像相關性。
1 系統原理及動力學分析
1.1 DNA突變原理
DNA序列由腺嘌呤(A)、胸腺嘧啶(T)、胞嘧啶(C)、鳥嘌呤(G)4種核酸堿基組成,其中A和T是互補的,C和G是互補的。在當前DNA編碼理論中,所有的信息都由這4種核苷酸表示。根據計算機二進制0和1的互補規則,00和11是互補的,01和10是互補的。因此,在編碼過程中將DNA堿基A、T、C、G分別編碼為00、01、10、11。顯然,編碼規則有4!=24種,但只有8種編碼方式滿足Watson-Crick互補規則,如表1所示。在傳統二進制加減法的基礎上,可得DNA的加減法。因此,根據8種DNA編碼規則,存在相應的8種DNA加減法規則。例如,在DNA編碼規則1的基礎上,DNA加法規則1和減法規則1如表2所示。
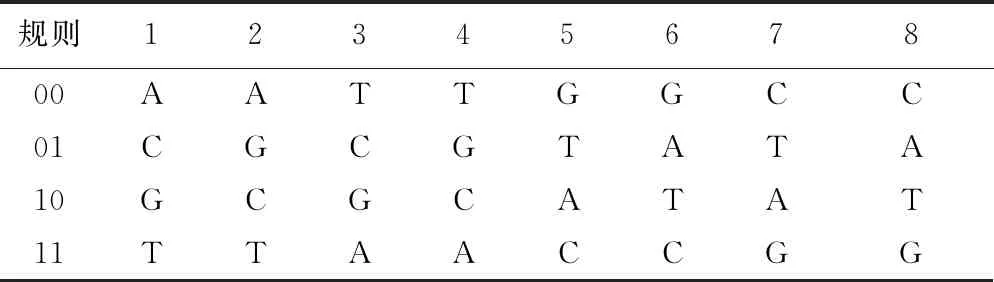
表1 DNA編碼法則Tab.1 The law of DNA encoding
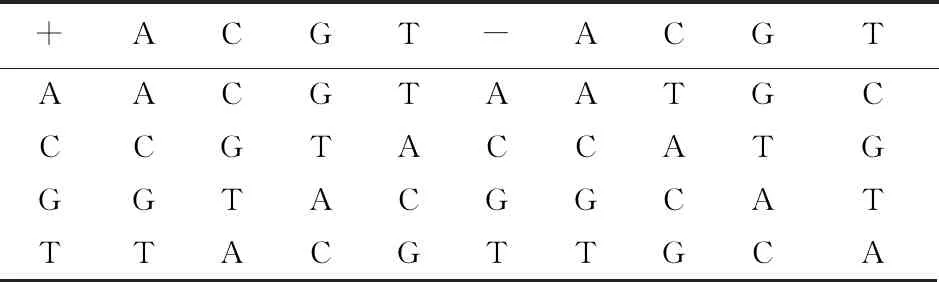
表2 DNA加減法則表Tab.2 Addition and subtraction rules of DNA
在DNA序列形成過程中,按照A與T、C與G配對。同時當L(xi)為xi的互補對時,每個堿基xi與它的配對堿基對都滿足式(1)。
(1)
由式(1)可知,互補堿基對有6種合理組合,如式(2)所示。加密過程中,隨機選擇6種互補組合規則中的一種互補置換,達到像素擴散的目的。
(2)
在DNA互補配對過程中,會出現DNA突變現象,也稱堿基置換突變,是指DNA分子中一個堿基被另一個不同的堿基取代所引起的突變,即點突變。因為基因突變的發生限定在特點時間、特定突變的個體、特定突變的基因,都是隨機突變的結果。這種突變的應用可滿足圖像信息加密隨機性高、變化率大的需求。
1.2 混沌動力學分析
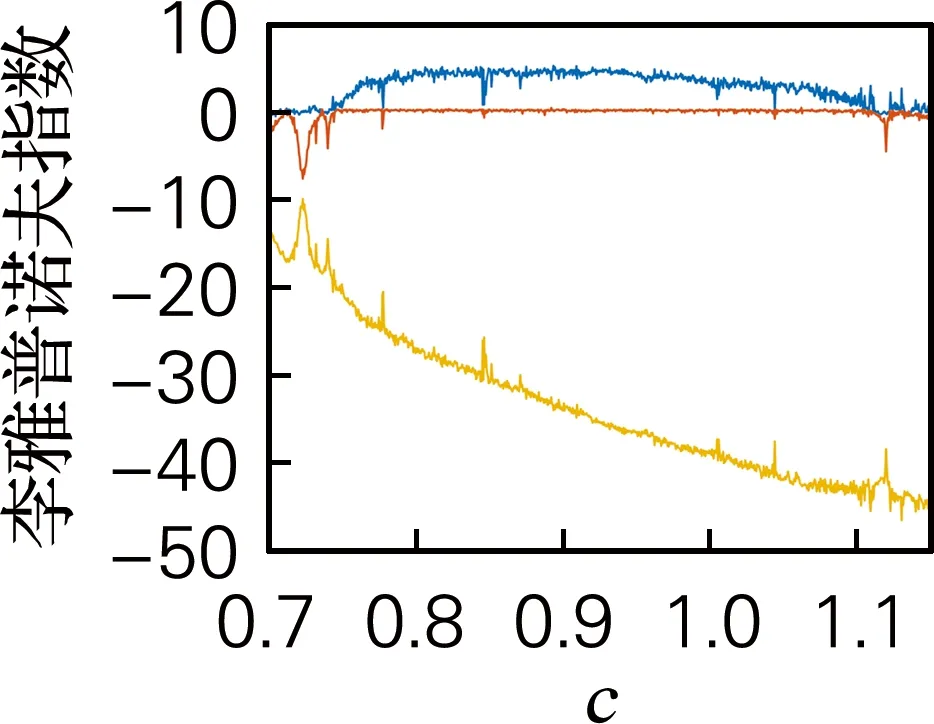
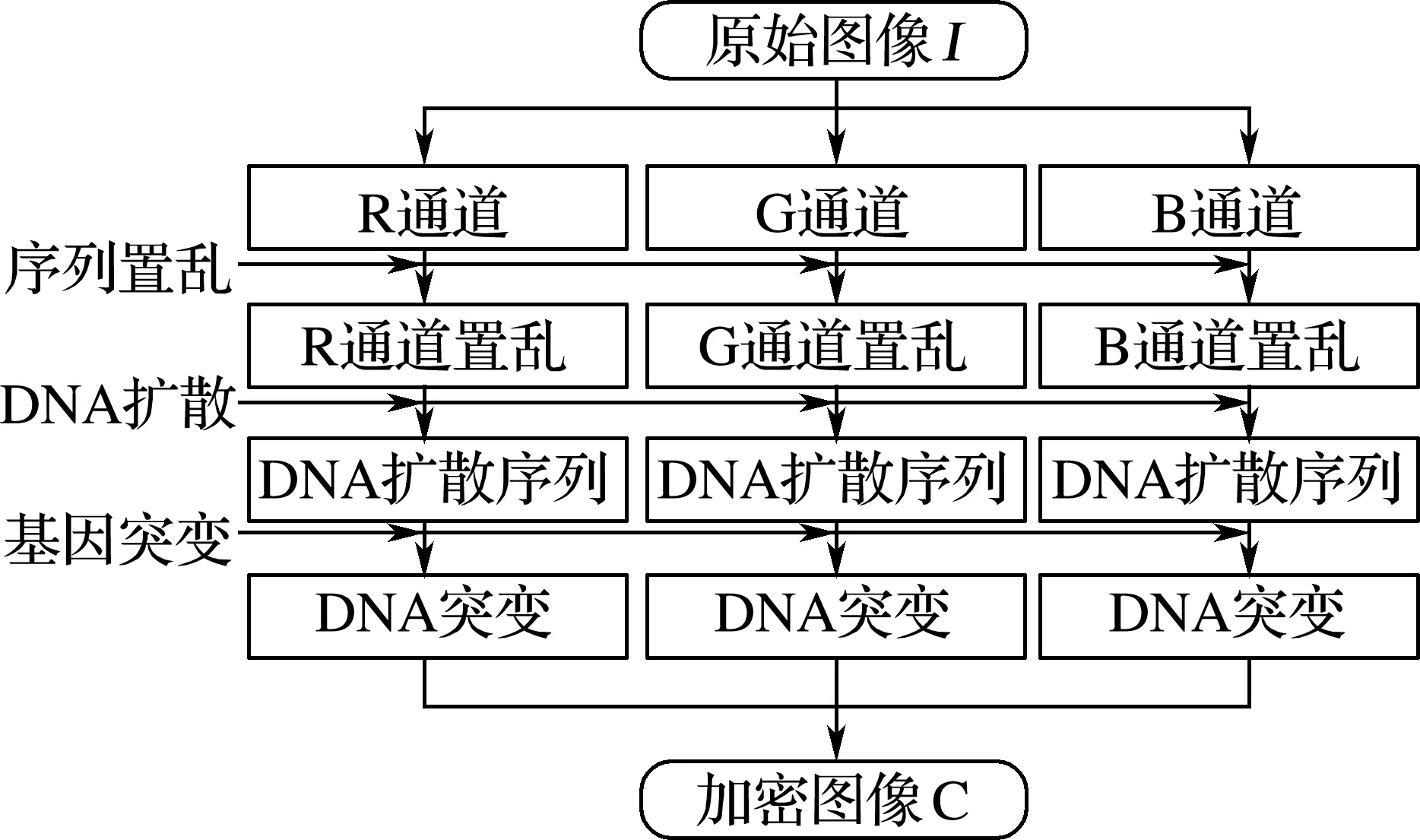
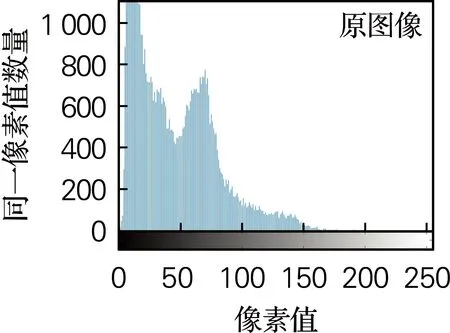
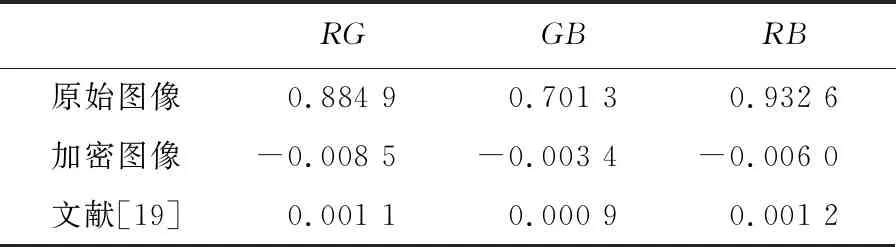
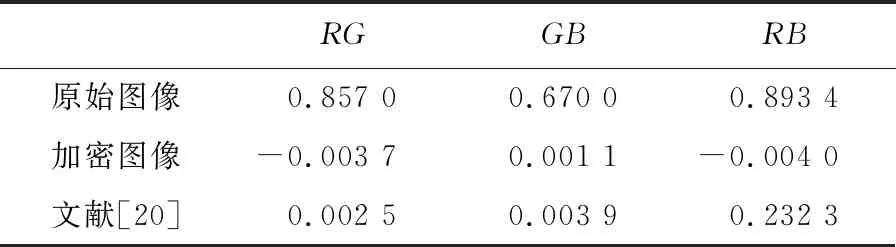
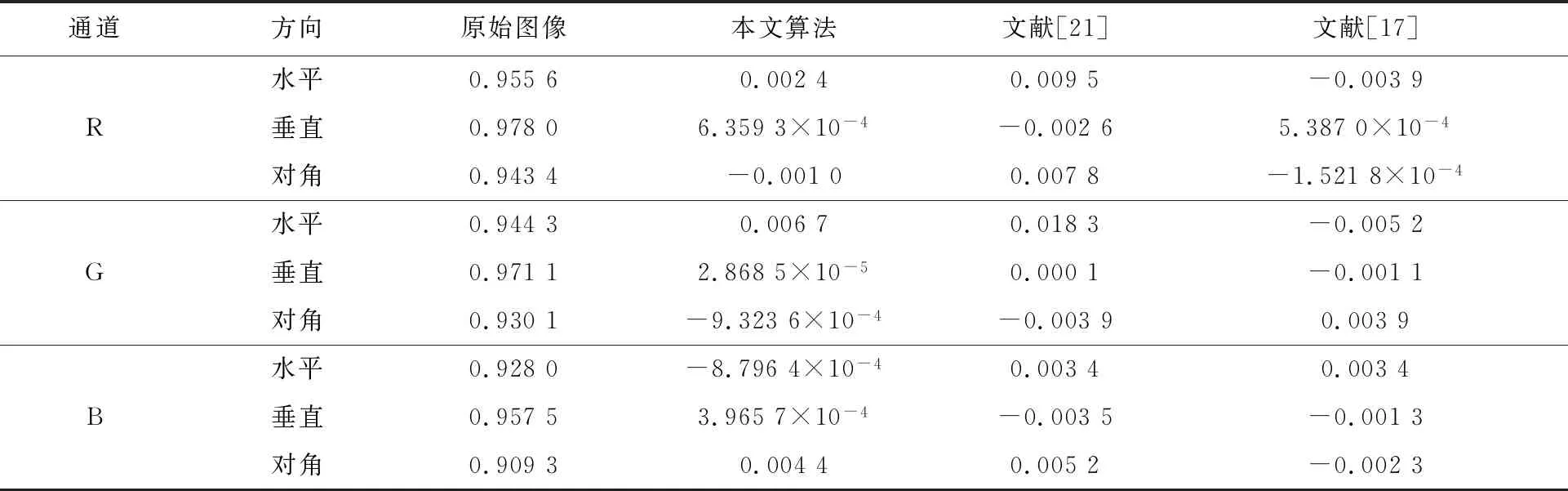
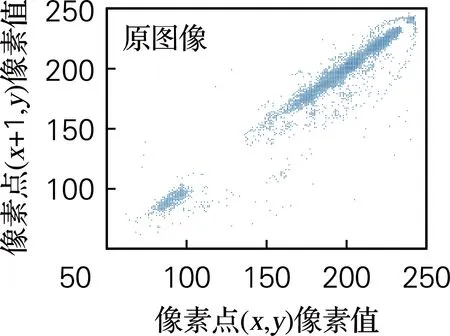
所提出的基于Lu系統和Chen系統的分數階三維簡化統一系統數學模型如式(3)所示[18]。其中x1,x2,x3為混沌系統的狀態變量,q(0 (3) 令c=0.9,q=0.9,時間步長為t=0.001 s,系統初值[x0,y0,z0]=[0.1,0.2,0.3]。此時,得到系統的混沌吸引子相圖如圖1所示。同時計算可得李雅普諾夫指數(L1,L2,L3)=(5.082 4,0,-33.903),由于系統只有一個正的李雅普諾夫指數值,并且所有的李雅普諾夫指數之和為負,所以系統在當前條件下處于混沌狀態。當系統參數q=0.9,c∈[0.7:1.15]時,得到李雅普諾夫指數譜與分岔圖如圖2所示。由圖2可看出,系統在c∈[0.7,1.15]的大部分范圍內是混沌的,僅僅c=0.84附近出現了一個周期窗口。 (a) x-y平面 (a) 李雅普諾夫指數 綜上所述,分數階簡化統一系統具有較大的混沌域,分布在一個較大的區域內,這意味著該系統具有良好的隨機性。 所提出的圖像加密算法由像素點隨機置亂和DNA擴散兩部分組成。像素點隨機置亂部分利用三維分數階混沌映射生成隨機混沌序列對圖像R通道、G通道和B通道進行無序化處理。DNA擴散部分利用三維分數階混沌系統生成混沌序列結合DNA編碼操作,對置亂后的圖像R通道、G通道和B通道進行擴散運算,即互補操作、加法操作、突變操作。主加密過程如圖3所示。 圖3 加密算法流程圖Fig.3 The flow chart of algorithm 具體加密步驟如下: 步驟1輸入大小為H×W×3的彩色原始圖像(H為圖片高度、W為寬度)。設置密鑰值c,x0,y0,z0,m,n,c0,α,β,Li,根據式(4)算法得到分數階三維混沌系統的新初值條件: (4) (5) 步驟2設定L=max(H,W),讓混沌系統根據新的初始條件迭代(m+L)次,并將之前的m個值丟棄,以提高初始值的靈敏度。同時,置亂算法的置亂規則由式(6)確定。 (6) 式中:Cx,Cy,Cz為矩陣置換系數,k為對應置換點的坐標。 步驟3將彩色圖像I分解為R、G、B部分,然后將R、G、B部分轉換為3個矩陣,并分別對3個像素矩陣元素的點進行點移位處理。具體操作:矩陣中的每個坐標點都與之唯一相對的置換點置換。重新構造矩陣后,得到置亂圖像矩陣TK。置亂后的像素矩陣根據DNA運算規則進行擴散,包括相加運算、互補運算和突變運算。具體見步驟4~9。 步驟4將置亂后矩陣中的數值以二進制數值表示,得到H×W×8的二元矩陣R1、G1和B1。然后依照DNA編碼規則,將二進制矩陣轉化為H×W×4的DNA序列矩陣S1,S2和S3。 步驟5設定混沌系統的初始值x0,y0,z0,得到混沌序列,通過迭代式(1):n+H×W次,并丟棄前n個值。根據式(7)得到k1,k2和k3三個序列。 k1=mod((xi)×1016,256)k2=mod((yi)×1016,256)k3=mod((zi)×1016,256) (7) 將得到的序列整形后進行DNA編碼,得到一組新的DNA序列矩陣k1,k2和k3,矩陣大小與像素矩陣大小相同。 步驟6用得到的偽隨機數序列矩陣k1對加密圖像的像素矩陣S1進行擴散操作。具體方式是:利用規定好的堿基配對規則,將像素S1矩陣原有的DNA排序擾亂,生成新的DNA排序,再與偽隨機序列矩陣k1進行加法計算,得到新的加密圖像像素矩陣N1。 步驟7利用基因突變中的堿基置換突變規則,加大圖像信息加密隨機性。在DNA擴散操作后,每一像素點的值已經被表示為4個堿基組成的加密組合(如ATCG),將每組內的堿基隨機互換。得到新的加密圖像像素矩陣C1。 步驟8利用DNA編碼規則對C1矩陣進行反編碼,并還原成十進制數表示的像素矩陣C。 步驟9輸出最終加密圖像結果,完成加密過程。 解密算法是一個恢復原始圖像的過程。首先將加密圖像重新編碼成DNA序列矩陣,之后利用突變原理進行反向還原,還原后運用DNA減法原理以及DNA互補原理,從而得到加密圖像的原DNA序列。利用編碼規則對DNA序列反編碼,利用三維系統生成混沌序列并轉變為偽隨機序列來還原加密圖像的置亂步驟,得到最初的已解密像素矩陣,并編碼成十進制像素矩陣,組合后得到解密圖像。 解密算法: 步驟1輸入加密后的大小為H×W×3的圖像C,利用DNA編碼原則對矩陣編碼形成C1,元素矩陣的大小為H×W×4。 步驟2利用基因突變堿基置換突變,進行逆突變變化。生成原始DNA加密后的矩陣。 步驟3根據三維系統生成的混沌序列并轉化后的偽隨機系列。利用DNA減法計算,還原加密圖像的DNA序列,得到加密擴散序列,擴散序列,再依據規定好的堿基配對原則與生成的偽隨機序列逆運算,得到未全部解密的DNA元素矩陣S1。 步驟4重新整形S1為大小H×W矩陣,并進行二進制編碼,形成元素矩陣TK。由三維混沌系統生成序列,再由式(6)生成點置換規則,對矩陣反置亂。 步驟5對元素矩陣進行點置亂計算。具體過程為三個像素矩陣中的每個點都與之唯一相對的置換點k置換,得到解密圖像矩陣TK3。 步驟6恢復三個二進制像素矩陣為十進制,通過組合輸出解密圖像。完成解密過程。 為驗證所提加密算法的有效性。使用大小為256×256的Lena圖像進行算法測試。設定分數階混沌系統的參數、初始值和階數。基于Matlab 平臺,得到相應的實驗測試結果如圖4所示。實驗結果表明,該算法能有效地對圖像進行加密和解密。 (a) 原始圖像 對于一個好的圖像加密算法,需要有足夠大的密鑰空間來抵御蠻力攻擊。在加密方案中,如果計算精度為10-5,密鑰c,q,x0,y0,z0對應的密鑰空間大小約為2249;對于密鑰的另一部分m,n,c0,α,β,Li,因為DNA有4種堿基,8種編解碼規則和6種互補規則,所以得到密鑰空間22×26×220=228。所提算法的密鑰空間是2277,所提出的算法空間足夠大,可以經受蠻力攻擊。 密鑰敏感性是指當密鑰發生微小變化時,恢復后的圖像將與原來的圖像完全不同,這意味著加密算法是良好的密鑰敏感性。實驗中,分別對解密算法的密鑰(x0+10-15),(y0+10-15),(z0+10-15),(c+10-15)進行了改變,將加密的圖像進行解密算法運算,得到相應的結果如圖5所示。顯然,這些恢復后的圖像與正常解密后的圖像完全不同。因此,該算法對密鑰非常敏感。 (a) 正確解密圖像 3.4.1 直方圖分析 直方圖反映圖像中像素值的分布。加密圖像的直方圖應該是平坦的,能夠很好地抵抗統計攻擊。原始彩色Lena圖像及其加密圖像的直方圖如圖6所示。可以看出,加密圖像的直方圖非常平滑,因此,攻擊者不會通過分析密文直方圖得到任何有用的圖像信息。所以,此算法可以防止統計攻擊。 3.4.2 圖像相關系數 對于原始圖像,相鄰像素之間有很強的相關性。一個好的圖像加密算法應該打破相鄰像素之間的相關性。計算像素相關系數見式(8)。 (a) R通道 (8) 式中:x、y為不同圖像的像素值,cov(x,y)為協方差,E(x)和D(x)分別表示x和N的平均值和方差,N是圖像中像素的總數。 通過計算,表3、表4列出了加密后的圖像在R、G、B分量中相同及相鄰的位置的相關系數。原始Lena圖像和加密后的圖像在R、G、B通道的相關系數如表5所示。表格數據表明,原始圖像具有顯著的相關性,而加密圖像的相關性很小說明加密算法的效果達到了要求。 表3 相同位置相關系數Tab.3 Correlation coefficients of identical position 表4 相鄰位置相關系數Tab.4 Correlation coefficients of adjacent position 表5 RGB通道相關系數Tab.5 Correlation coefficients in R,G,B channels 為了清楚地看到原始圖像和加密圖像的相關性,圖7給出了Lena圖像R通道各方向上的相關性分布。如圖7所示,原始圖像在相鄰像素之間具有極強的相關性,原始圖像的所有像素點都是沿著對角線聚集的。然而,加密圖像的像素點分散在整個平面上,這表明加密圖像中不同像素點之間的關系在加密圖像中大大減少。因此,圖像加密算法具有抵抗靜態攻擊的能力。 信息熵是證明圖像隨機性的一個重要的測量值,由式(9)確定。 (9) 式中:p(mi)表示符號mi出現的概率,L表示所有的特征點mi的數量。對于L=256圖像,信息熵的理論值為8。加密圖像在R、G、B通道中的信息熵值,以及R、G、B分量S的組合,新算法的計算結果接近于8。因此,加密后的圖像具有良好的隨機性。 差分攻擊是指密文對純文本的敏感性。一般采用像素數變化率(NPCR)和統一平均變化率(UACI)來檢測差異攻擊。 NPCR和UACI的計算公式: (10) 式中:L為所有圖像像素的個數。C和C1分別為同一位置變化前后的像素值,通過式子(11)得到D(i,j)。 (11) (a) R通道水平方向 在實驗測試中,只需要改變原始圖像的一個隨機像素,用一輪加密進行10次測試,就可以得到NPCR和UACI的平均值。計算結果表明,該算法的NPCR和UACI分別為大于99.79%和33.45%,表示該算法足以抵抗差分攻擊。 統計各項性能,我們與已有的算法進行對比,如表6所示。從密鑰空間、信息熵、抗差分攻擊性能。證明該加密方法,有更好的安全性。 表6 系統性能比較Tab.6 System performance comparison 基于ADM算法,研究了三維分數階簡化統一系統的動態特性和圖像加密應用。動力學分析表明,該混沌系統具有更復雜的動態特性,其混沌態分布在一個較大的參數范圍內,這說明它更適合于混沌密碼體制。在此基礎上,為了保證數字圖像在信息傳輸和存儲過程中的安全傳輸,基于分數階混沌系統和基于DNA突變算法的算術運算,本文設計了一種新的圖像加密方案。加密算法的安全性能分析表明,分數階簡化統一系統及DNA突變原理在圖像加密算法中得到了應用,不僅可以有效地對圖像進行加密,而且提高了圖像加密算法的安全性。為密碼學、保密通信和信息安全等領域提供了相關的理論基礎和實際應用基礎。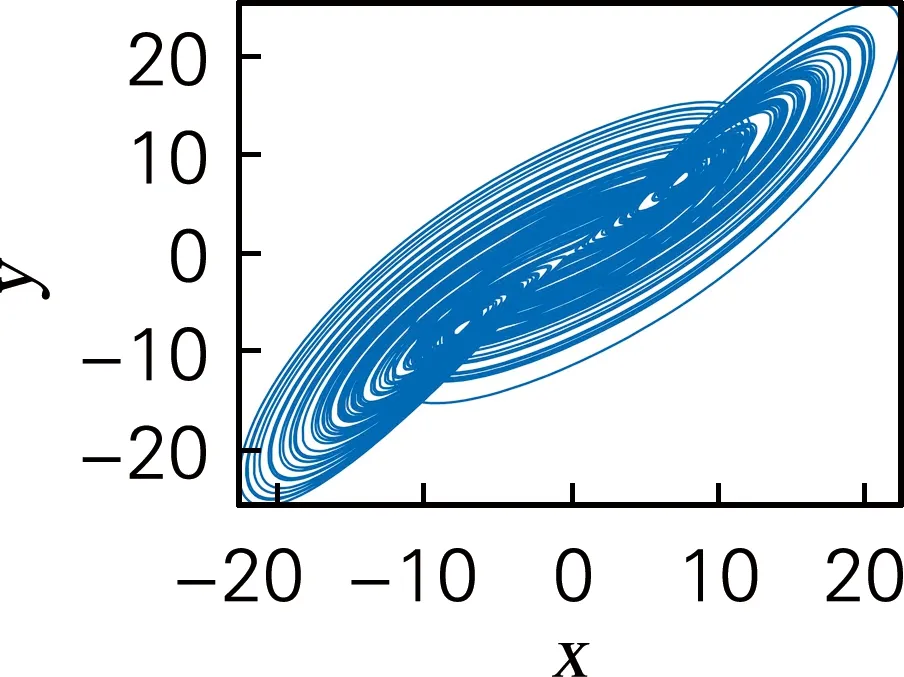
2 圖像加密和解密方案
2.1 加密方法
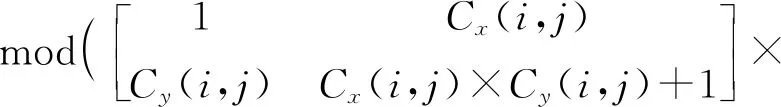
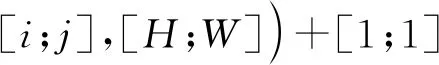
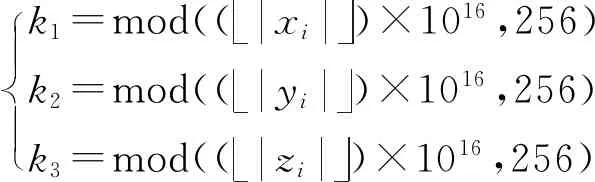
2.2 解密方法
3 仿真與性能分析
3.1 算法仿真結果

3.2 密鑰空間分析
3.3 密鑰敏感性分析

3.4 統計性能分析
3.5 差分攻擊分析
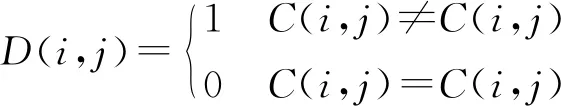
3.6 系統性能比較

4 結 論

