基于遺傳算法的多目標拆卸線平衡問題

李 勇，王 雅 君，王 耐 東，李 焜

(大連工業(yè)大學(xué) 機械工程與自動化學(xué)院,遼寧 大連 116034)

0 引 言

拆卸是產(chǎn)品回收的基本動作，提取有用部件，回收有害部件，做到循環(huán)經(jīng)濟和綠色制造。拆卸線平衡問題(disassembly line balancing problem，DLBP)成為近年的研究熱點。Gungor等[1]分析了DLBP問題，指出與裝配線平衡問題的區(qū)別；Avikal等[2]采用一種啟發(fā)式算法求解DLBP問題，但僅適用于解決小規(guī)模問題；Altekin等[3]采用線性規(guī)劃方法優(yōu)化DLBP，但無法解決大規(guī)模問題；Kalayci等[4]采用遺傳算法處理DLBP問題，但算法較早收斂于局部最優(yōu)解。文獻[5-6]以AND/OR圖規(guī)劃和整數(shù)規(guī)劃，以最大化利潤來優(yōu)化拆卸線問題；Kalayci等[7]采用模擬退火算法，局部搜索能力強，但耗時長，獲得全局最優(yōu)解能力弱。實際的拆卸線問題需要兼顧多個目標，單一的優(yōu)化往往不能更好地協(xié)調(diào)拆卸線。文獻[8-9]在實際生產(chǎn)中解決多目標條件下的DLBP問題；丁力平等[10]提出了基于Pareto的蟻群算法，通過支配關(guān)系尋找最優(yōu)前沿，以拆卸線空閑時間、平滑系數(shù)、成本等為優(yōu)化目標，但未考慮零件其他影響平衡的指標。

針對上述研究的不足，本研究提出一種改進的遺傳算法，在均衡空閑時間、平滑系數(shù)基礎(chǔ)上，結(jié)合零件拆卸時環(huán)境、資源，提出新優(yōu)化目標，通過具體實例，分析并驗證該算法對求解此類問題的優(yōu)越性。

1 數(shù)學(xué)模型

1.1 基本參數(shù)

假設(shè)每個待拆零件作為一個拆卸任務(wù)，零件數(shù)為n(也叫拆卸任務(wù)數(shù))；T={1，2，3，…，n}為所有任務(wù)的集合；N為工作站數(shù)；CT為生產(chǎn)節(jié)拍，tk為第k個工作站上分配的所有拆卸任務(wù)作業(yè)時間之和。

1.2 決策變量

拆卸線平衡優(yōu)化不僅要考慮作業(yè)任務(wù)的均衡分配，還包括環(huán)境、資源等，待拆產(chǎn)品可能包含有害物質(zhì)，如重金屬、化學(xué)毒物，在拆卸作業(yè)中應(yīng)優(yōu)先考慮。拆卸主要是回收和利用有剩余價值的零件，拆解中應(yīng)盡快拆除價值大的零件。為使待拆產(chǎn)品的分解作業(yè)時間最小化，拆卸動作方位的變換次數(shù)也納入優(yōu)化空間，縮短拆卸作業(yè)時間。

考慮拆卸線平衡的5個目標，并對其優(yōu)化。5個目標包括最少工作站數(shù)F1，平衡各個工作站空閑時間F2，見式(1)和(2)。

minF1=k

(1)

(2)

將兩個目標歸納合并，以式(3)和(4)同時優(yōu)化均衡閑置時間與最小化工作站數(shù)兩項任務(wù)。

(3)

(4)

優(yōu)先拆卸高需求部件指標F3，優(yōu)先拆卸危害大的部件指標F4；最少改變方向進行拆除F5。

(5)

(6)

(7)

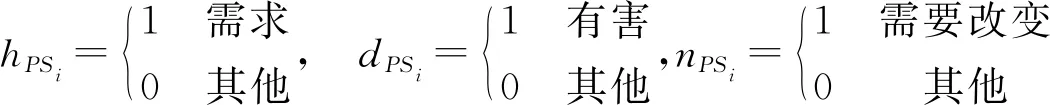
引入方向指標用來評價解序列，該數(shù)值越小，即拆卸過程中方向改變量越少，則該解越優(yōu)。式(8)表示拆卸過程相對零件與工作站的各個方向。

(8)

將方向指標用決策變量的形式進行表述為

(9)

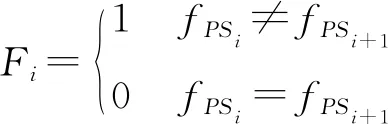
綜上，多目標拆卸線平衡表示為

minF=(F3，F(xiàn)4，F(xiàn)5，F(xiàn)6)

(10)

s.t.

(11)

(12)

(13)

約束條件式(11)為設(shè)置工作站數(shù)應(yīng)不低于理論工作站數(shù)、不多于拆卸任務(wù)數(shù)，式(12)為各工作站內(nèi)拆卸時間不超過生產(chǎn)節(jié)拍，式(13)表示拆卸順序必須滿足拆卸優(yōu)先關(guān)系。

2 算法模型求解

2.1 編 碼

常用的編碼方式有二進制0-1編碼、實數(shù)編碼、浮點數(shù)編碼等[11-12]。針對拆卸線作業(yè)任務(wù)的現(xiàn)實情況，使用一種基于作業(yè)順序先后的染色體編碼規(guī)則，將n個拆卸元素排列于一排，相應(yīng)對應(yīng)一個基因位，并按作業(yè)順序優(yōu)先圖將這些元素分配到各工作站中，站中工序的加權(quán)時間值不得高于預(yù)定的生產(chǎn)節(jié)拍，按工作站中工序的排序進行編碼。利用插零[13]方法來表示當(dāng)前工作站的作業(yè)元素開始(或結(jié)束)位置，染色體中n個作業(yè)、k+1個0、n+k+1長，相鄰兩個0間的作業(yè)元素為同一個工作站。

2.2 初始種群生成

初始種群的好壞對進化過程優(yōu)劣性影響明顯，影響算法運行效率。采用拓撲排序隨機搜索生成初始種群，確保初始種群中個體的多樣性與解的多樣性。根據(jù)作業(yè)優(yōu)先順序流程，在作業(yè)任務(wù)全集內(nèi)(種群)尋找無任務(wù)前驅(qū)的任務(wù)i，并放入新集T1中，在作業(yè)順序圖中隨即刪除任務(wù)i及與其相關(guān)的緊后順序；重復(fù)上述操作，直至任務(wù)集合為空集結(jié)束分配任務(wù)，每步選好的任務(wù)放到對應(yīng)的基因位，所得序列即為初始可行拆卸序列。

2.3 解 碼

編碼采用的是基于任務(wù)的一維數(shù)組解序列，無法由其確定個體優(yōu)劣性，需要將解序列分配到各工作站[14]，操作過程為開啟第一個工作站j=1；初始化當(dāng)前站內(nèi)時間和剩余時間；尋找解序列上的任務(wù)i，當(dāng)所分配的任務(wù)時間超過當(dāng)前剩余時間，則分配失敗，隨機開啟新工作站，初始化當(dāng)前站內(nèi)時間和剩余時間；反之，將任務(wù)i分配到當(dāng)前站中，并更新站內(nèi)時間和剩余時間，并循環(huán)直至遍歷解序列。對每個個體的編碼及工作站間插零，能確保種群中各工作站與任務(wù)分配，提高算法的可視化[15]。

2.4 適應(yīng)度

適應(yīng)度函數(shù)在GA搜索進化中起評價個體優(yōu)劣的作用。僅利用目標函數(shù)即可在解空間內(nèi)完成系統(tǒng)優(yōu)化，在遺傳算法空間中，按一定規(guī)則將目標函數(shù)轉(zhuǎn)換成個體適應(yīng)度，并評價適應(yīng)度值以實現(xiàn)解空間中可行解優(yōu)劣的判斷。

2.5 遺傳算子

2.5.1 選 擇

最常用的選擇方法是輪盤賭法，采樣思路為經(jīng)選擇的個體后代遺傳的概率與適應(yīng)度值成正比，適應(yīng)度函數(shù)評價越高，進入下一代的概率也就越大，個體進入下一代的概率為它的適應(yīng)度值與整個種群中個體適應(yīng)度和的比例，假設(shè)種群中個體數(shù)為M，個體被選擇的概率為

2.5.2 交 叉

交叉操作是形成新個體的重要方式，從選擇完成的種群中任取的兩個染色體，采用特定規(guī)則互換部分基因，重組后形成新個體[16]。

由于傳統(tǒng)常規(guī)方法中的隨機交叉方式往往會得到大量重復(fù)且沖突的現(xiàn)象，產(chǎn)生不可行解，影響算法的運行效率，故采用兩點映射交叉法，于父代染色體隨機確定兩個交叉點，對父代兩染色體于交叉點間部分基因排序并采用部分映射，保存交叉點兩側(cè)的基因并放到新個體中，從而產(chǎn)生兩個新的后代個體。假設(shè)隨機選取第3、5基因位為交叉點，父代中兩個交叉點前的序列{6，3，7}、{2，4，9}得以保留，兩交叉點間的序列{8，5，1}在父代2中的順序為{1，5，8}，具體過程如圖1所示。

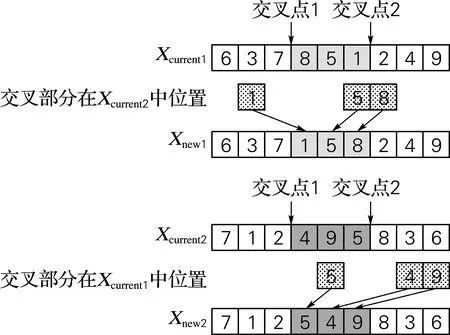
圖1 交叉示意圖Fig.1 The diagram of crossover

2.5.3 變異操作

類似于交叉操作，作業(yè)受優(yōu)先關(guān)系的約束，變異也會產(chǎn)生不可行解。采用單點基本位變異，在父代染色體隨機產(chǎn)生一變異點(圖2中的4位置)，并根據(jù)作業(yè)優(yōu)先順序，找出變異點的前后工序，保留前驅(qū)任務(wù)與以前的基因位置、緊后任務(wù)與以后的基因位置，隨機將變異元素4插入染色體中前驅(qū)、緊后工序間的最近基因位，再整合以上基因的3部分生成新的子代染色體。若選取的變異位置沒有可選的插入位置，則重新選取變異點。

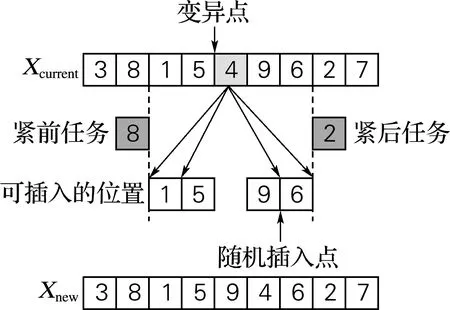
圖2 變異操作示意圖Fig.2 The diagram of mutation

2.6 結(jié)束準則

GA作為一種反復(fù)迭代的搜索工具，通過多次進化循環(huán)而無限逼近最優(yōu)值，而非恰好計算出最優(yōu)解，因此須確定終止條件，確定遺傳迭代的代數(shù)。在算法的初始時，迭代次數(shù)設(shè)置要盡量小，視情況增加迭代，當(dāng)?shù)螖?shù)超過要求的最大代數(shù)時，算法停止。

2.7 算法實現(xiàn)流程

初始種群的個體雖然是可行的，但較難保證個體最優(yōu)在運算初期產(chǎn)生，為提高這種尋優(yōu)解性能，于算法初期增大交叉、變異的概率。而在迭代后期，要想保障適應(yīng)度高的優(yōu)良基因，可降低交叉、變異概率。采用一種自適應(yīng)交叉概率Pc如式(1)，變異概率Pm如式(2)。

(1)

式中：m為迭代次數(shù)，Pcmax為最大交叉概率，Pcmin為最小交叉概率。

(2)

式中：M為最大迭代次數(shù)，Pmmax為最大變異概率，Pmmin為最小變異概率。

算法實現(xiàn)的步驟：

步驟1參數(shù)的確定：選定種群規(guī)模NP及Pc、Pm的值；

步驟2初始化種群：令t=0，滿足節(jié)拍約束和作業(yè)優(yōu)先順序的前提下產(chǎn)生初始種群P(0)，個體數(shù)為NP；

步驟3適應(yīng)度評估：計算第t代種群中每個個體的適應(yīng)度值；

步驟4選擇操作：從第t代種群中選擇NP個個體并把它們復(fù)制到t+1代中；

步驟5交叉操作；

步驟6變異操作；

步驟7最優(yōu)保存策略；

步驟8循環(huán)：令t←t+1，滿足停止條件即結(jié)束；反之，轉(zhuǎn)向步驟3。

3 實例驗證

3.1 DLBP實例計算

一個零件數(shù)為8的計算機部件的拆卸信息如表1所示，同時，零件拆卸任務(wù)優(yōu)先關(guān)系如圖3所示，利用改進的遺傳算法求解。參考文獻[17]用MATLAB R2012b在Windows7系統(tǒng)平臺實現(xiàn)上述算法程序，對上述實例求解，工作站均為最小站數(shù)4，危害指標H均為7，需求D=211，方向指標R=7。表2為求得的最優(yōu)解。表3為最優(yōu)拆卸系列解及平衡后的工作站。其中，拆卸任務(wù)1、5被分配到工作站1，工作站2主要負責(zé)拆卸任務(wù)3、6、2，以此類推。且最優(yōu)解較早地將高需求零件3、6、2和危害零件7進行了拆除，允許有7個方向的改變，算法運算時間不到1s，所得解的平衡和危害目標與文獻[9]相同，需求指標則優(yōu)于文獻[11]，方向指標比文獻[11]多一個。因而所得解的總體性能優(yōu)于文獻[11]。

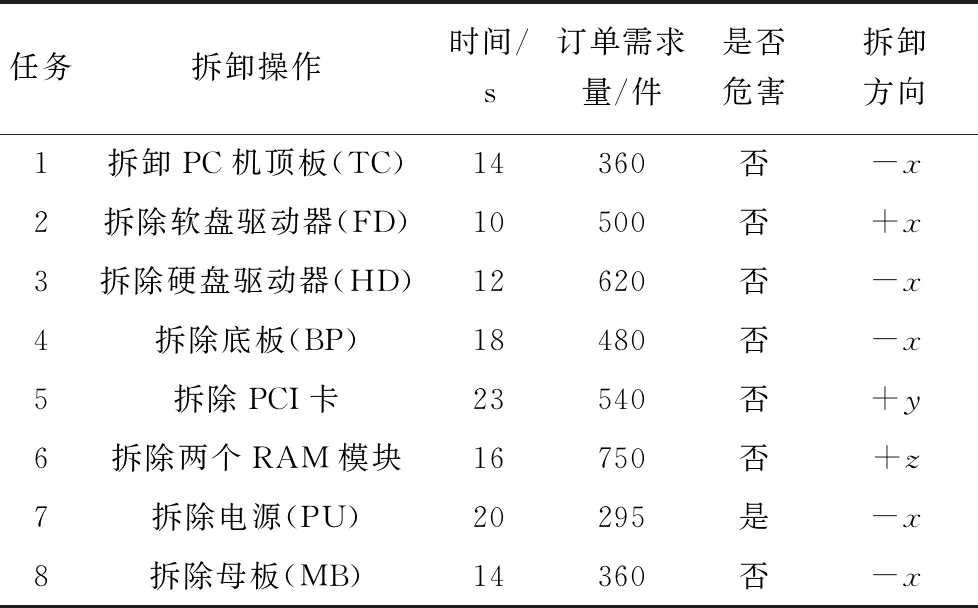
表1 8個零件的拆卸信息Tab.1 Disassembly information for eight components

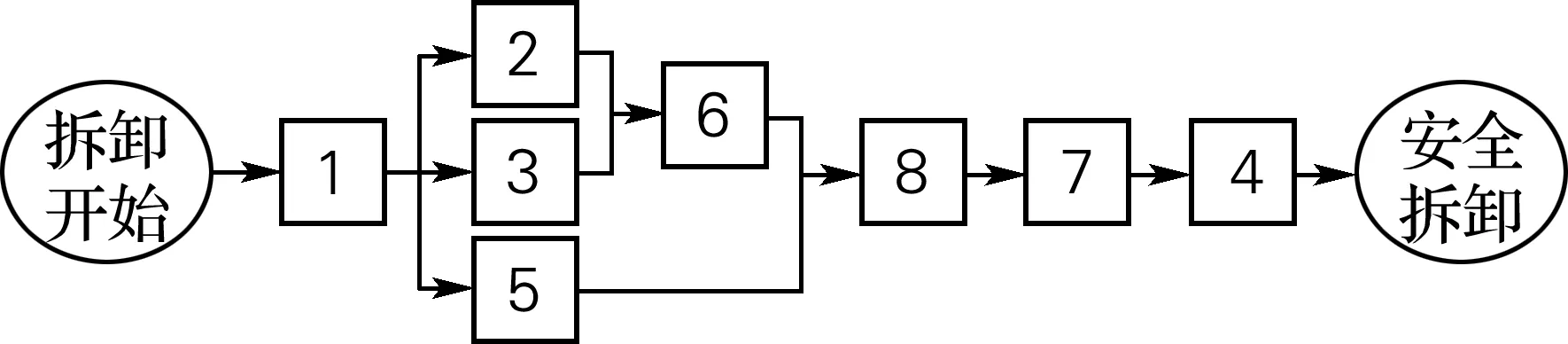
圖3 零件拆卸任務(wù)優(yōu)先關(guān)系Fig.3 Work priority relationship of components

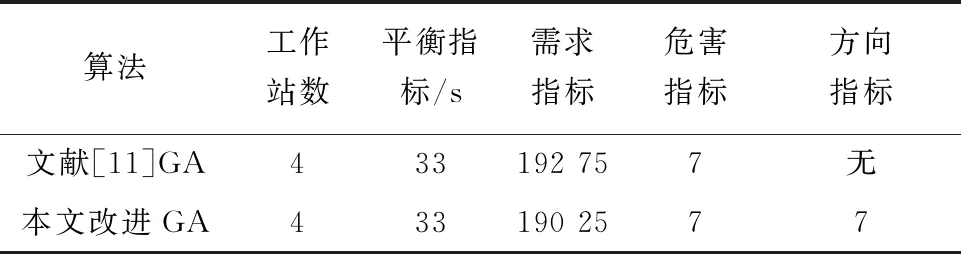
表2 改進GA與標準GA優(yōu)化結(jié)果對比Tab.2 The comparison of optimization results between improved GA and standard GA

4種單目標求得的最優(yōu)解如表2所示，并參考文獻[9]中的參數(shù)設(shè)計結(jié)合DLBP問題，針對解的質(zhì)量和算法效率經(jīng)反復(fù)測試，將參數(shù)設(shè)置為NP=100，M=100，Pcmin=0.5，Pcmax=0.95，Pmmin=0.005，Pmmax=0.01，經(jīng)計算后取最優(yōu)值，并分析運算時間，最優(yōu)序列結(jié)果見表3。將改進GA與文獻中的標準GA進行對比，從中得出測試結(jié)果在處理該問題上與標準算法相比較突出，能起到平衡的作用，且運行時間更短。

表3 DLBP最優(yōu)拆卸系列解Tab.3 Optimal disassembly series solution of DLBP

3.2 發(fā)動機拆卸實例應(yīng)用

以文獻[18]中的汽車發(fā)動機拆卸實例為研究對象，對發(fā)動機進行完全拆卸。原企業(yè)中未考慮拆卸危害與需求，可變性差，不能及時地適應(yīng)拆卸任務(wù)的變化，現(xiàn)利用改進的遺傳算法對發(fā)動機缸體拆卸線進行改進，相關(guān)數(shù)據(jù)如表4所示。

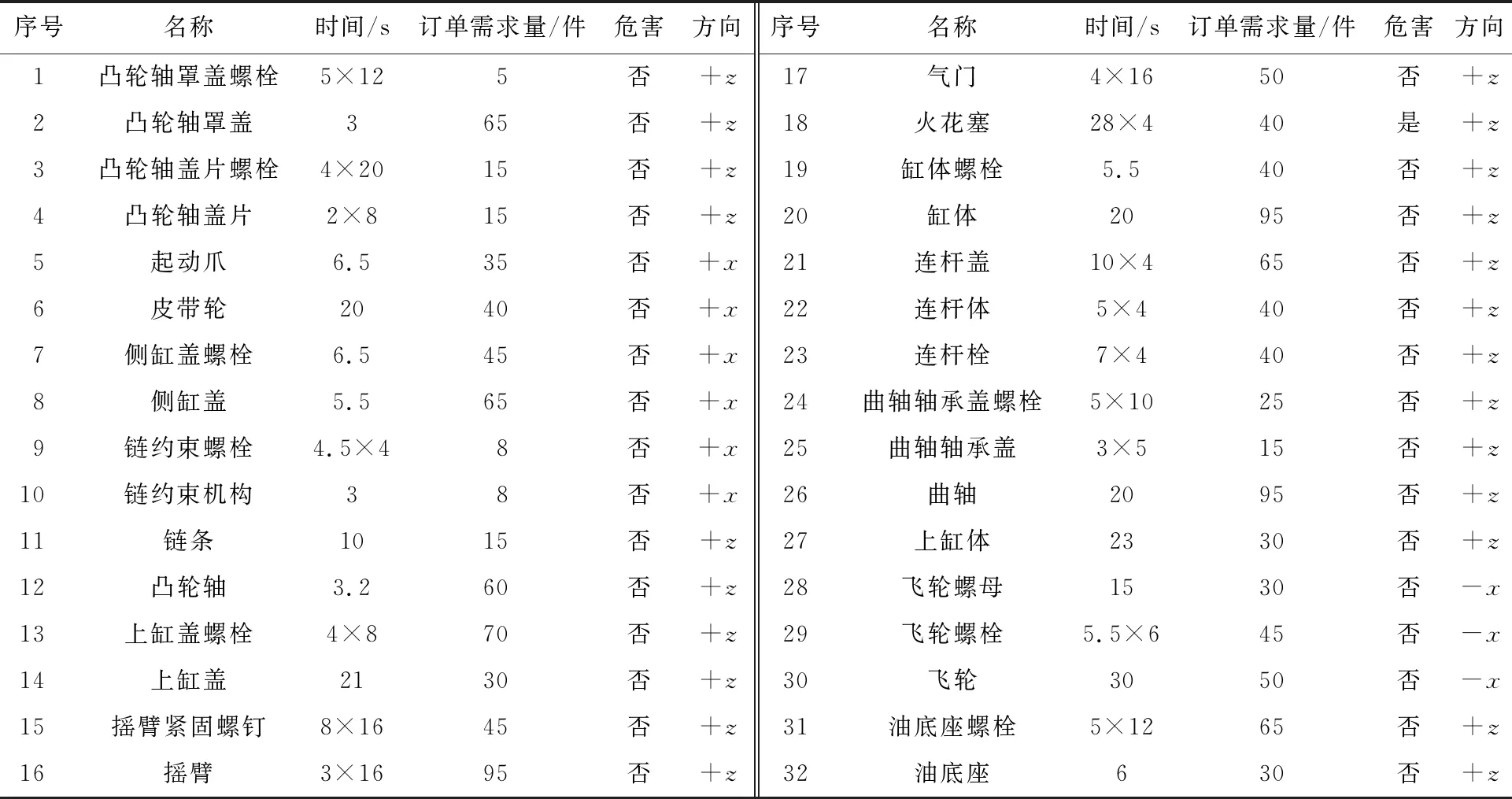
表4 汽車發(fā)動機作業(yè)零件及要素Tab.4 Working parts and elements of automobile engine

將拆卸線的汽車發(fā)動機作業(yè)順序矩陣錄入，在MATLAB2012b上進行編程，節(jié)拍CT=120 s，算法參數(shù)為NP=50，MaxGen=150，GAP=0.9。對多個目標函數(shù)進行優(yōu)化，并取得了預(yù)測的結(jié)果，跳出局部最優(yōu)解取得更優(yōu)解，搜索能力明顯提高，優(yōu)化結(jié)果如圖4所示。線平衡結(jié)果如圖5所示，直線型布局優(yōu)化結(jié)果中工作站數(shù)為15，而U型線布局站數(shù)為9，所以U型布局能做到最小化工作站數(shù)，具有一定經(jīng)濟性。

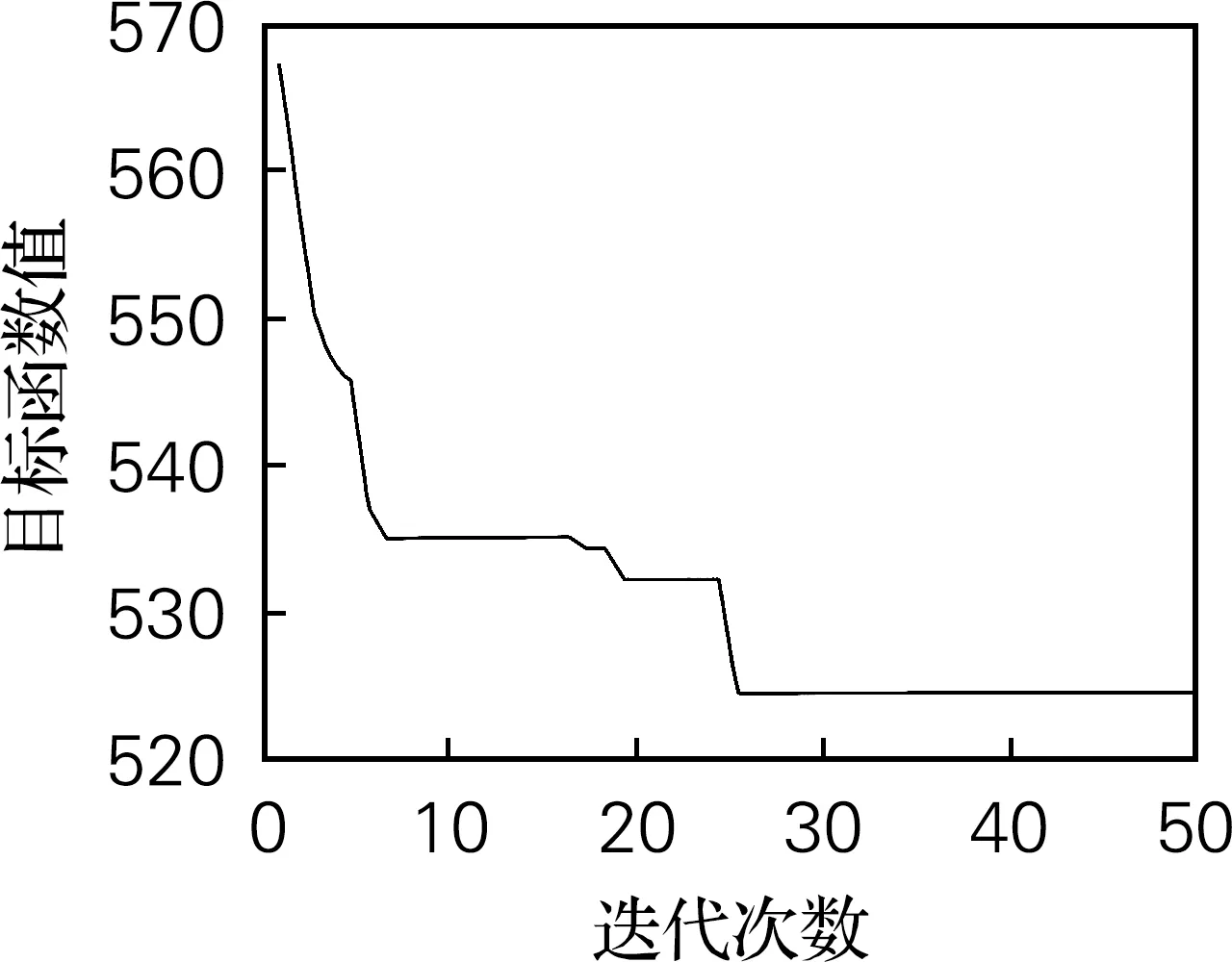
圖4 優(yōu)化結(jié)果Fig.4 The result of optimization

4 結(jié) 語

采用一種改進的遺傳算法求解多目標拆卸線平衡問題，在保證平衡的前提下，兼顧其他目標對平衡的影響，如危害、需求、拆卸方向等指標。采用實數(shù)編碼策略與拓撲排序和動態(tài)確定交叉、變異操作改進求得最優(yōu)解。算例表明DLBP-GA具有解決實際問題的可行性，能完成作業(yè)時間均衡，在此基礎(chǔ)上對多目標優(yōu)化問題具有很好的適應(yīng)性，可及時適應(yīng)拆卸任務(wù)的變化，為企業(yè)帶來更多的決策方案。

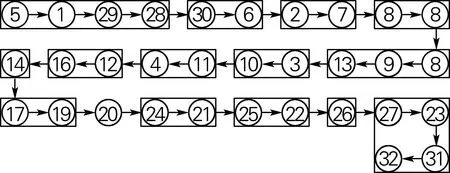
(a) 直線型