鋼管混凝土構件的介質多相性及導波檢測

劉鵬飛, 劉南希, 李祚華, 于洪濤, 滕 軍, 陳 杰

(1.深圳市建筑設計研究總院有限公司，深圳 518031；2.哈爾濱工業大學(深圳) 土木與環境工程學院，深圳 518055)

鋼管混凝土利用鋼管和混凝土兩種材料在受力過程中相互間的組合作用，充分發揮兩種材料的優點,一方面能改善混凝土的塑性和韌性，另一方面可避免或延緩鋼管發生局部屈曲，使鋼管混凝土具有承載力高、塑性和韌性好、經濟效果好和施工方便等優點[1]。鋼管混凝土構件一般作為柱子等關鍵受力構件，一旦失效將會降低建筑結構整體的安全性，造成損失[2]。因此，為了及時發現潛在的安全隱患，避免事故發生，對這種關鍵受力構件進行定期的檢測是十分重要的。基于導波的檢測方法成本較低、操作簡單、效率高、具有針對性又可滿足全面性，受到了廣泛關注[3-4]。

為了研究在不產生明顯頻散的激勵頻率下，鋼管混凝土介質多相性及軸向缺陷產生的導波回波信號的變化，筆者基于有限元軟件ABAQUS，分別創建鋼管砂漿骨料分層模型、基于Monte Carlo方法(一種統計模擬方法)的隨機圓形骨料模型和鋼管混凝土構件含軸向缺陷的模型，模擬導波在鋼管混凝土中的傳播情況，以此來分析導波回波信號的變化。

1 介質多相性引起的導波回波信號變化

鋼管混凝土構件中，混凝土骨料的粒徑是隨機分布的，試驗條件很難直接控制這一變量，但試驗結果卻會受到這種隨機分布的影響。基于伍君勇[5]對混凝土結構細觀模型進行的研究，筆者將混凝土看作一種復合材料，其由砂漿和骨料組成，具有多相性。由此，創建鋼管混凝土構件的有限元分析模型。

1.1 骨料層密度對導波傳播的影響

選用solid單元(一種有限元單元類型)，外層為鋼材，內層為混凝土材料，兩者間以tie(一種接觸方式)連接，模型全程處于彈性階段。鋼管混凝土模型長為3 200 mm，直徑為100 mm，壁厚為5 mm。

混凝土構件中骨料和缺陷的存在都會使導波的傳播路徑發生變化，引起導波散射和能量耗散。為研究骨料層密度的變化導致的導波回波信號的變化，在砂漿中按不同密度布置骨料層來進行模擬。單一骨料層和骨料層整體分布如圖1所示。以構件軸線與截面的交點為圓心，在直徑為90 mm的范圍內進行導波激勵，激勵頻率為10 kHz，導波信號為漢寧窗調制信號，提取到的響應信號如圖2所示。

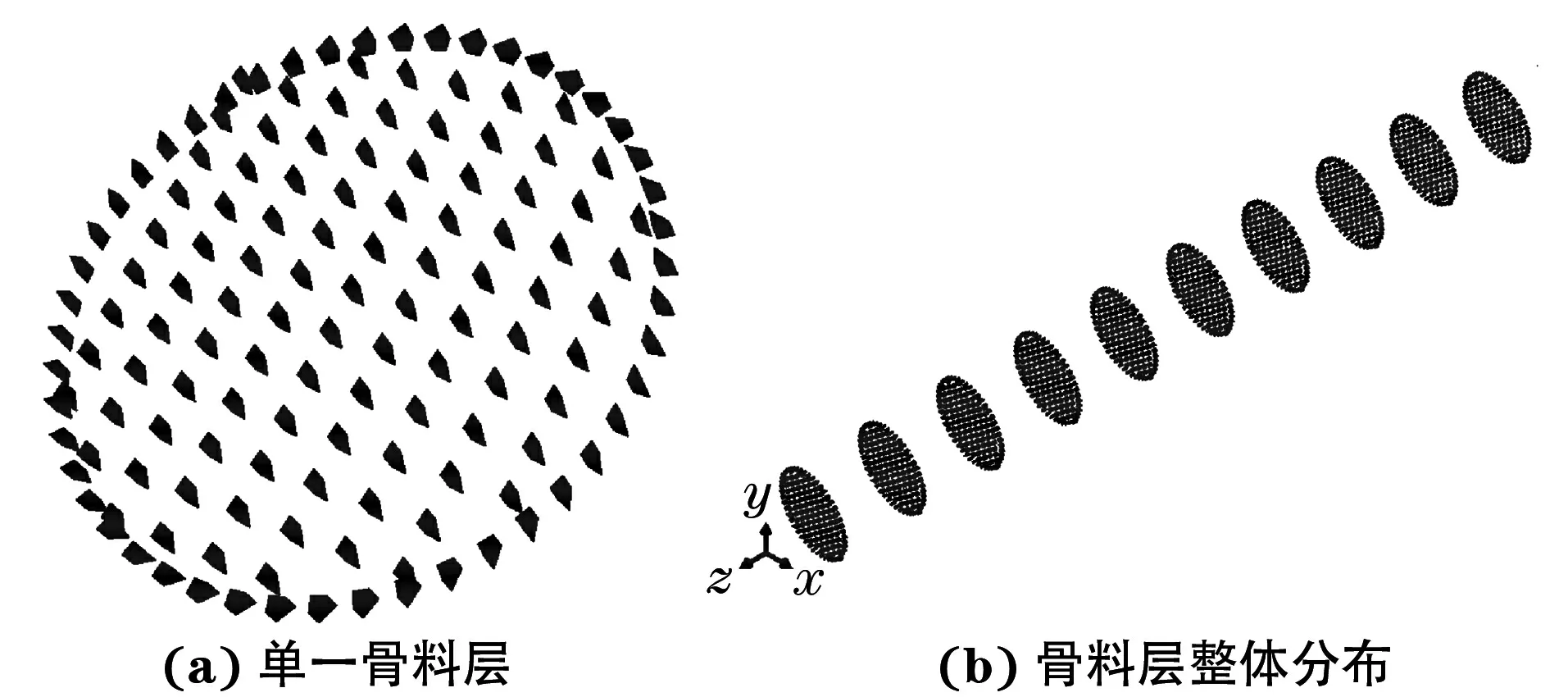
圖1 單一骨科層和骨科層整體分布示意

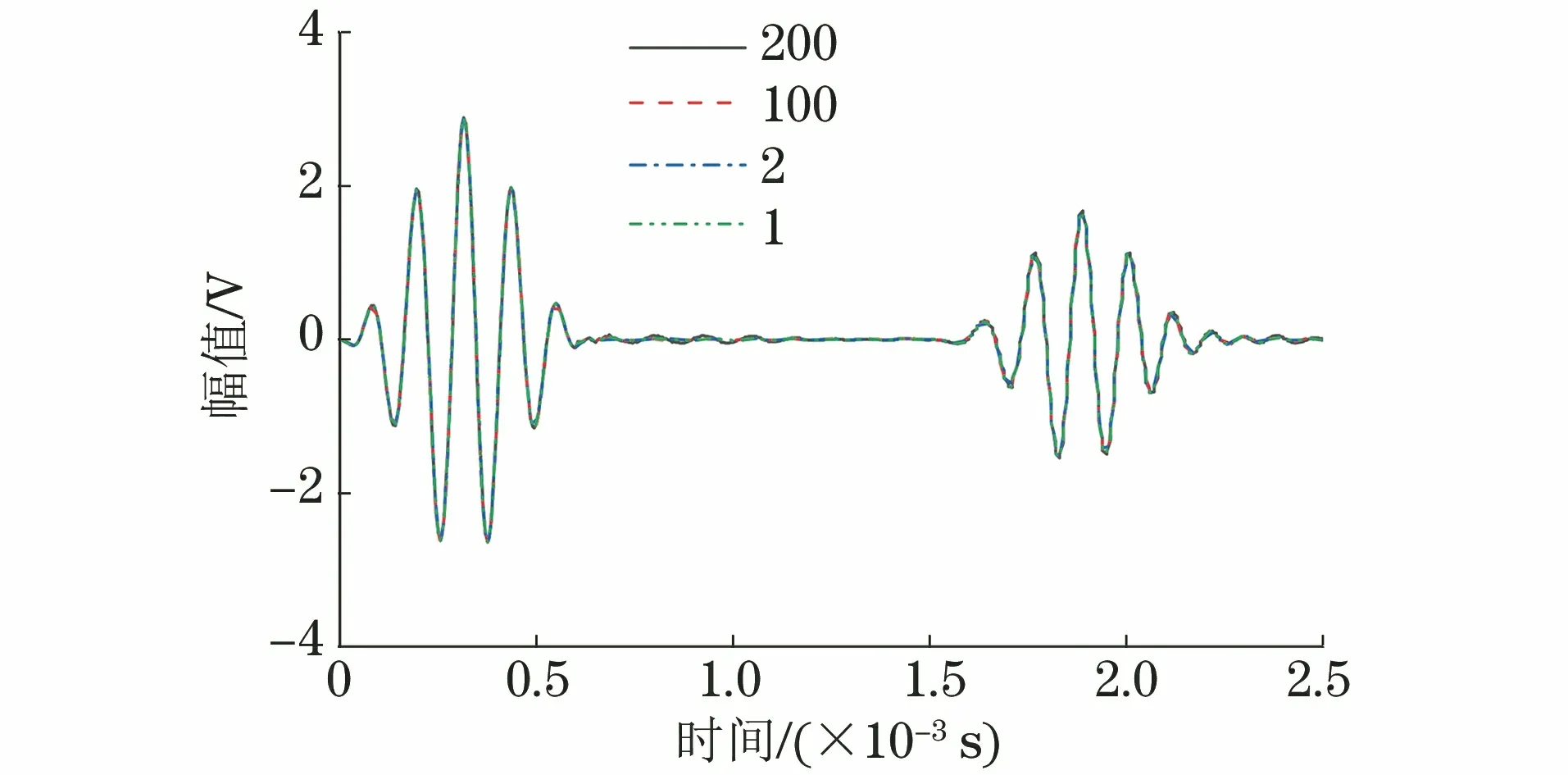
圖2 不同骨料層的導波回波信號

由圖2可知，對于整體信號而言，骨料層的密度變化導致的信號變化非常小。為研究不同骨料層密度的影響，放大信號的平穩段，得到如圖3所示的信號。

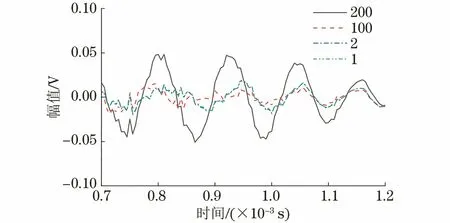
圖3 不同骨料層的導波回波信號(放大后)

由圖3可知，隨著骨料層密度增大，骨料反射回波幅值逐漸增大，提取信號中包含的骨料信息也增多。即便如此，相對于發射信號和回波信號的幅值骨料反射回波幅值極小。

1.2 骨料含量對導波傳播的影響

為研究骨料含量的變化導致的導波回波信號的變化，在ABAQUS軟件中創建混凝土構件的二維模型，通過改變骨料面積占比來模擬骨料的含量。

基于Monte Carlo方法，以骨料面積占比為指標，假定混凝土構件中骨料的分布和粒徑均為隨機的[6]，生成骨料面積占比分別為0%，20%，25%，30%，35%，40%，45%和50%的混凝土構件模型，在ABAQUS軟件中導入這些模型，創建隨機圓形骨料模型。圖4為骨料面積占比分別為0%，30%，40%和50%的混凝土構件模型，圖5為模型加載的示意圖。

圖4 不同骨料面積占比的模型

圖5 模型加載示意

在不同骨料面積占比的隨機圓形骨料模型的頂部提取響應信號進行分析。以骨料面積占比為30%的模型為例模擬導波傳播的過程，其在各時刻的響應云圖如圖6所示。

從圖6可以看出，初始狀態下試件整體處于零響應狀態。導波信號從試件的頂端出發，隨著時間增長，導波沿試件軸向傳播，并與試件邊界和內部骨料相互作用，內部響應情況逐漸復雜。導波到達試件底端后，開始反向傳播，并最終返回到試件頂端。

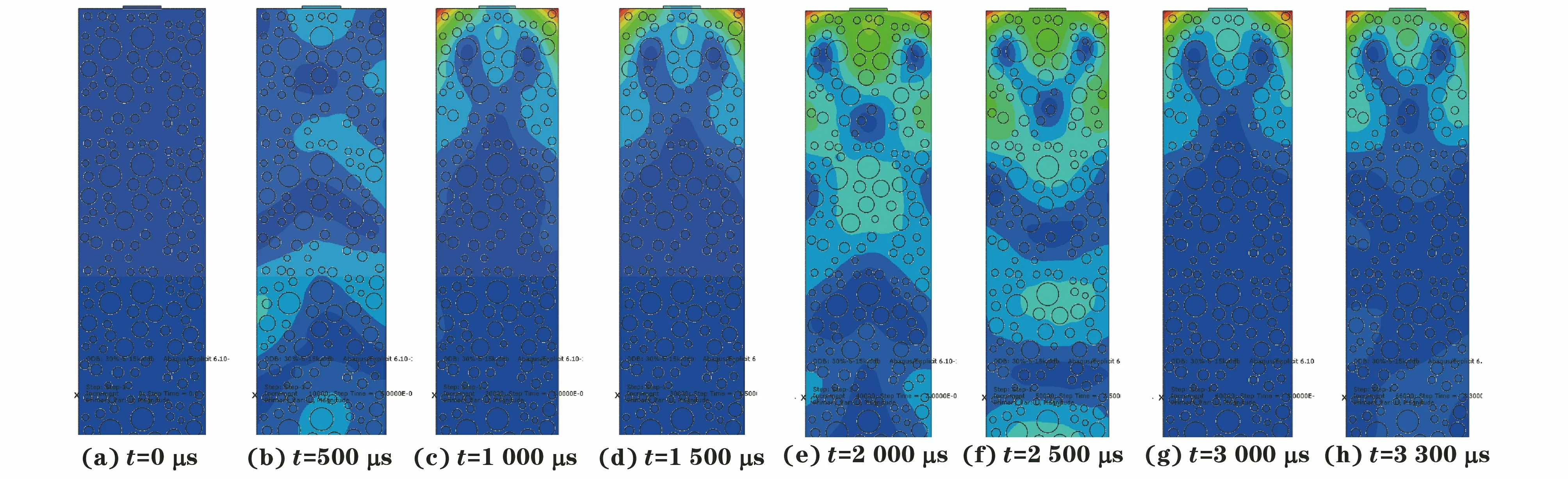
圖6 骨料面積占比為30%的模型在各個時刻的響應云圖

圖7為不同激勵頻率下，不同骨料面積占比的模型的導波回波信號。

從圖7可以看出，在相同的激勵頻率下，首波出現時間不隨骨料面積占比的變化而發生變化，但信號的幅值和傳播速度有明顯的變化。圖8所示為首波波峰與回波波峰的特征(出現時間和幅值)隨骨料面積占比變化的趨勢。

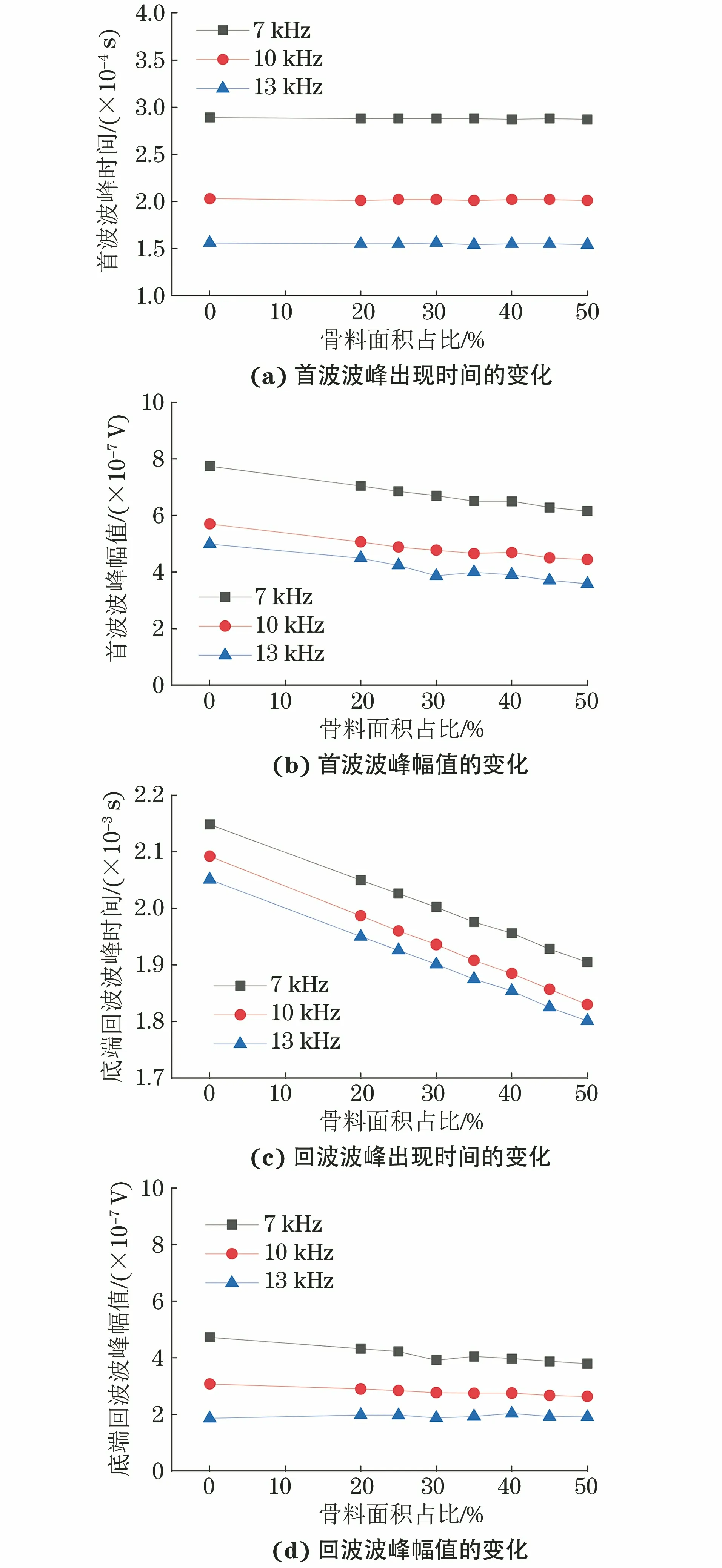
圖8 首波波峰與回波波峰特征隨骨料面積占比的變化趨勢

通過分析各個參數的變化，可以得到以下結論。

(1) 在頻散特性不明顯的激勵頻段內，激勵頻率不變而骨料面積占比增大時，首波波峰的出現時間并不隨之發生變化，但底端回波波峰的出現時間提前，且呈線性地提前了，這意味著導波傳播的速度呈線性地變快。

(2) 激勵頻率不變而骨料面積占比增大時，混凝土的彈性模量逐漸增大，導致首波波峰和回波波峰的幅值都逐漸減小。

(3) 首波波峰和底端回波波峰的出現時間隨著激勵頻率的升高而縮短，這意味著導波傳播的速度不僅與材料特性有關，也與激勵頻率有關。

(4) 首波波峰和底端回波波峰的幅值隨著激勵頻率的升高而降低，因為激勵頻率越大，波長越短，波的折射和反射現象越明顯，衰減越大；激勵頻率越小，波長越長，波的折射和反射現象相對較弱，衰減越小。

以首波波峰出現時間和回波波峰出現時間之差作為傳播時間，得到在頻散現象較弱的激勵頻段內，不同激勵頻率下，不同骨料面積占比的模型中導波傳播的速度變化曲線(見圖9)。

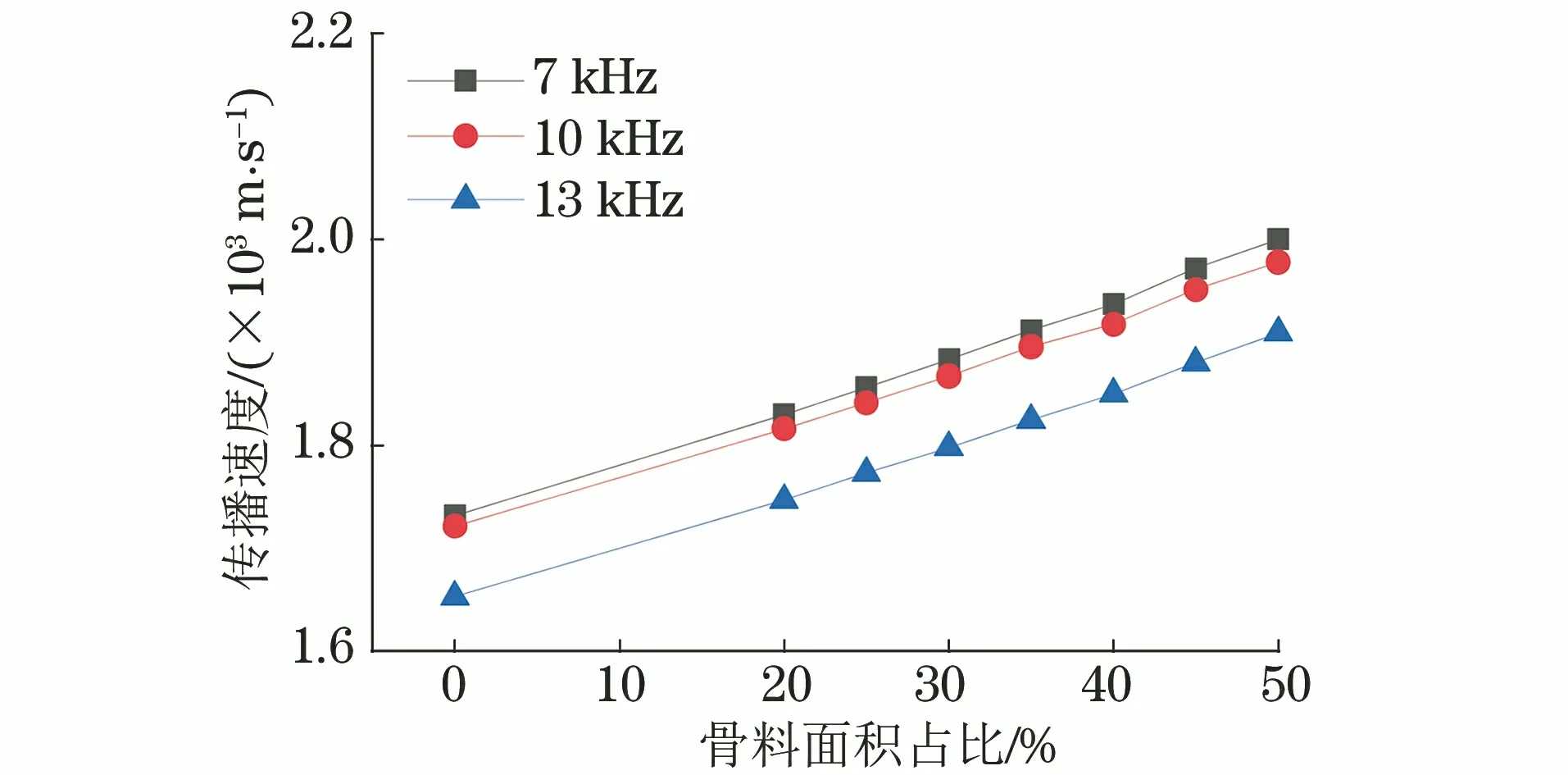
圖9 不同激勵頻率、不同骨料面積占比模型中導波傳播的速度變化曲線

由圖9可以得出以下結論。

(1) 在頻散特性不明顯的激勵頻段內，激勵頻率不變而骨料面積占比增大時，導波傳播的速度呈線性變快的趨勢。這是因為骨料含量的增大會使混凝土強度逐漸增大，試件的剛度也隨之增大。

(2) 導波傳播的速度隨著激勵頻率的增大而減小。

為進一步分析骨料面積占比導致的導波回波信號的變化，放大信號的平穩段如圖10所示，其最大幅值如圖11所示。

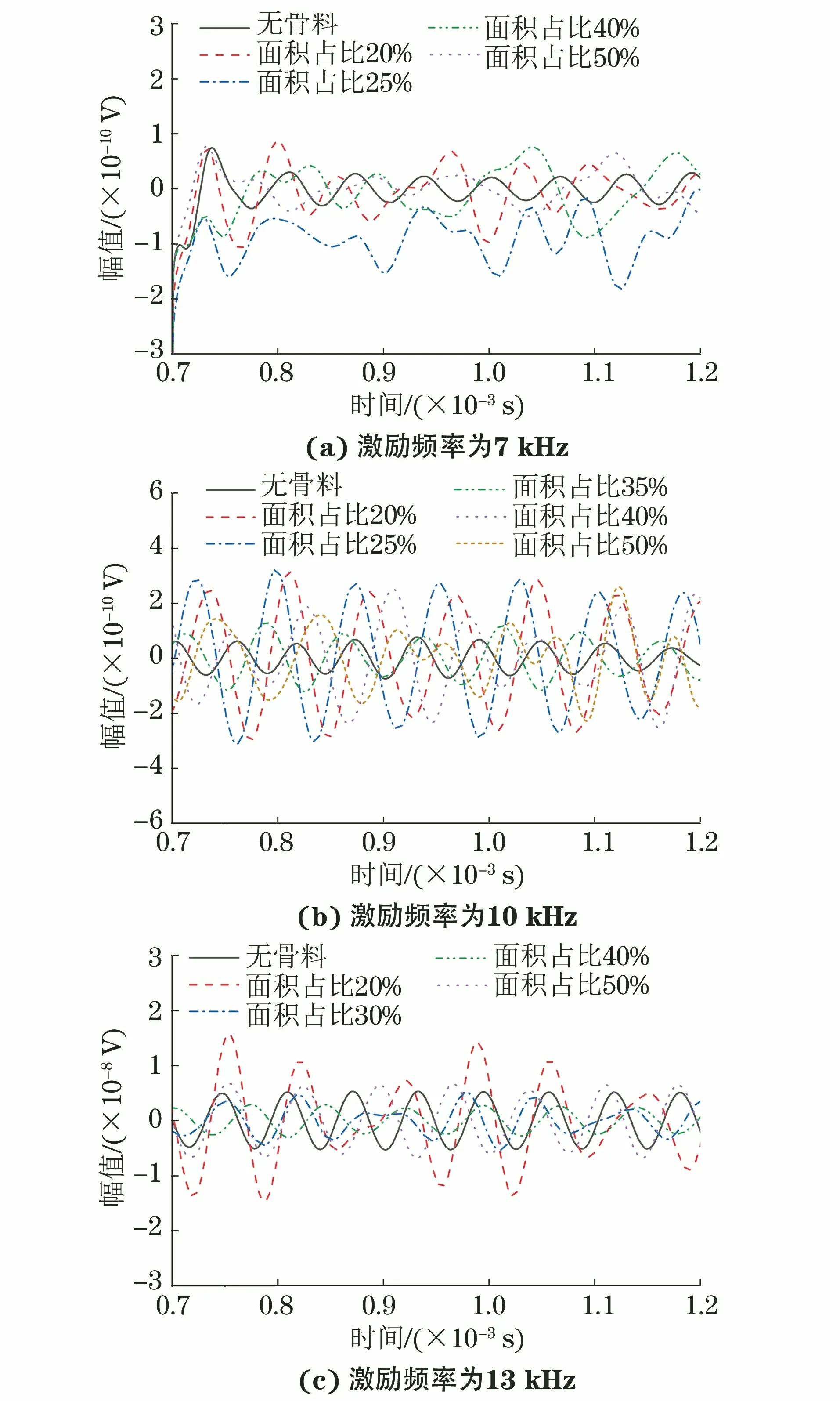
圖10 不同激勵頻率下不同骨料面積占比的信號平穩段

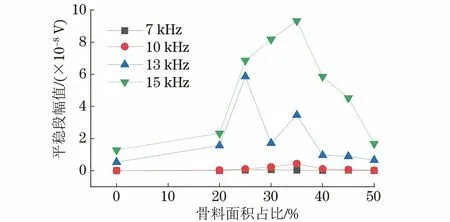
圖11 不同激勵頻率下不同骨料面積占比的信號幅值變化曲線

由圖11可見，對于同一激勵頻率，隨著骨料面積占比的增大，信號平穩段的最大幅值先逐漸增大，后逐漸減小。這是因為骨料含量的增加會使得頻散特性逐漸明顯，而根據前文分析，骨料含量的增加會使得混凝土強度和剛度逐漸增大，回波信號的幅值會隨之降低，在兩者的共同作用下就出現了這樣的現象。

為了對不同激勵頻率的導波回波信號進行分析，繪制如圖12所示的不同激勵頻率下不同骨料面積占比的信號幅值變化曲線。

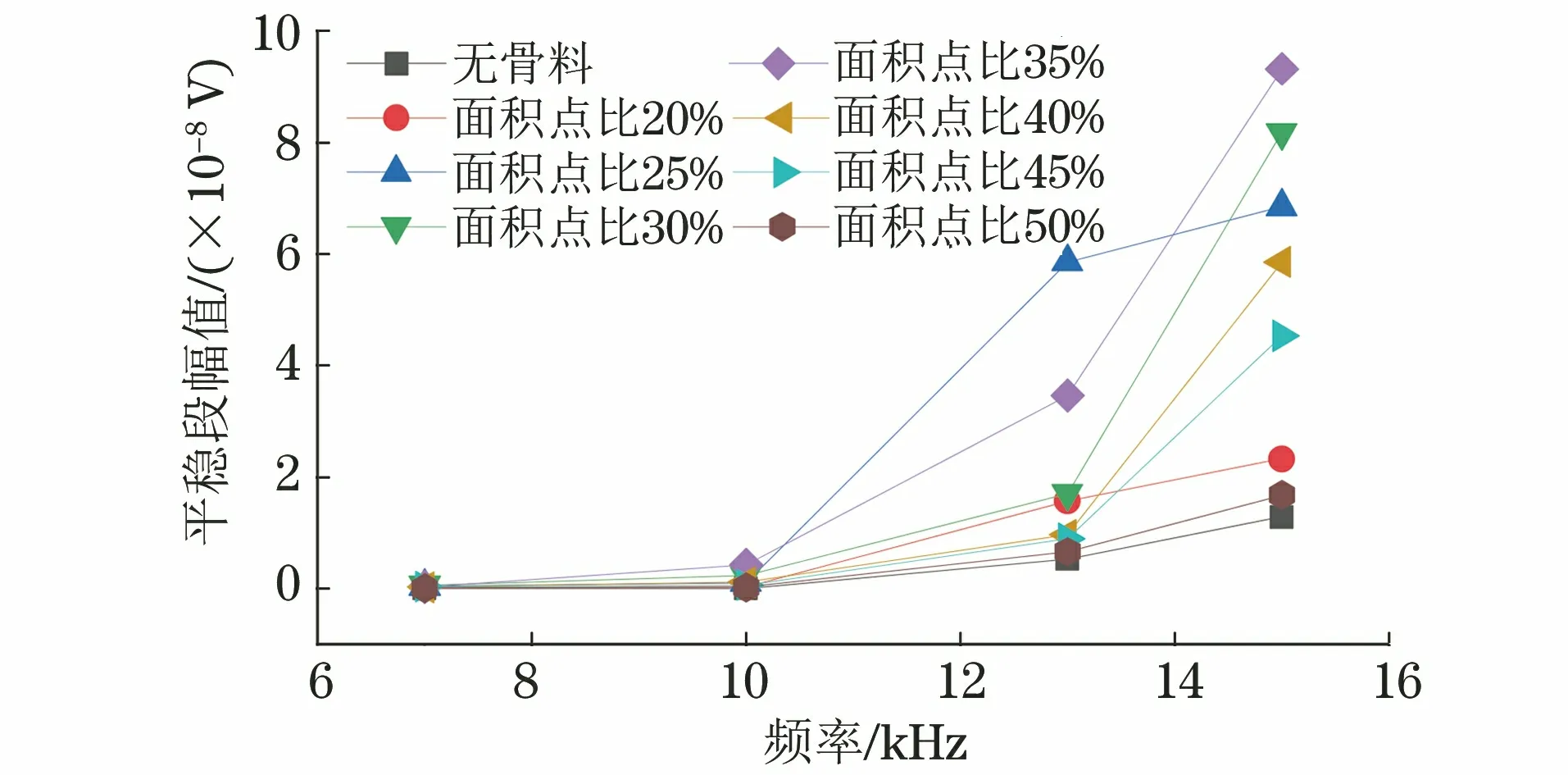
圖12 不同激勵頻率、不同骨料面積占比的信號幅值變化曲線

由圖12可知，在相同骨料面積占比下，隨著導波信號激勵頻率的增大，頻散特性的作用逐漸明顯，表現為信號平穩段的最大幅值逐漸增大。

綜上所述，激勵頻率不變而骨料面積占比增大時，首波波峰出現時間并不隨之發生變化，但幅值會逐漸減小；底端回波波峰出現時間呈線性提前，幅值也會逐漸減小。激勵頻率發生變化時，首波波峰和底端回波波峰的幅值隨著激勵頻率的升高而降低，導波傳播的速度隨之減小。在頻散特性不明顯的激勵頻段內，檢測混凝土構件的導波回波信號在無缺陷情況下的信號平穩段幅值遠小于激勵信號段幅值和底端回波信號段幅值，可忽略不計。因此，缺陷檢測的關鍵就是確定頻散特性不明顯的激勵頻段。

2 鋼管混凝土構件軸向缺陷引起的導波回波信號變化

材料、應力和缺陷等均會對鋼管混凝土構件中導波的傳播產生影響，使導波發生折射和反射，導波的能量也隨之衰減[7]。利用導波的這種特性來對鋼管混凝土構件中的軸向缺陷進行檢測。在ABAQUS軟件中創建直徑為100 mm的含軸向缺陷的鋼管混凝土構件模型，并設置不同截面尺寸和軸向長度的缺陷。該節僅探究缺陷截面尺寸和軸向長度引起的導波回波信號的變化，缺陷位置固定在鋼管混凝土模型中部。

將截面損傷定義為截面環形面積的缺失，首先對缺陷直徑為10 mm的構件進行檢測，不同長度缺陷的響應信號如圖13所示。

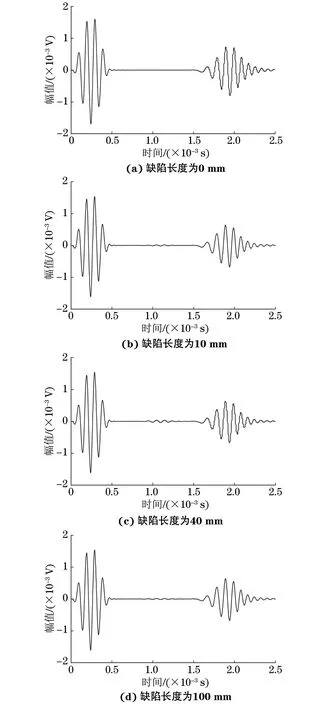
圖13 不同長度缺陷的響應信號(缺陷直徑為10 mm)

由圖13可知，信號平穩段對缺陷十分敏感，即使是截面損傷率僅為0.99%的情況下也可以很容易地判斷出構件是否存在缺陷。對直徑為10 mm的中心缺陷以及大徑為30 mm、小徑為20 mm的環形缺陷的信號平穩段的最大幅值進行統計，繪制其隨缺陷長度的變化曲線，結果分別如圖14，15所示。

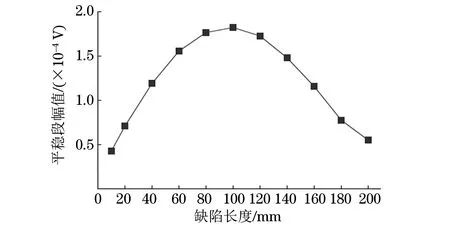
圖14 中心缺陷信號幅值隨缺陷長度的變化曲線

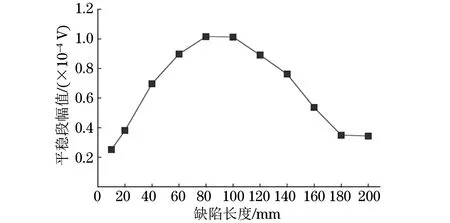
圖15 環形缺陷信號幅值隨缺陷長度的變化曲線

由圖14,15可知，當缺陷截面尺寸一定時，隨著缺陷軸向長度的增大，缺陷響應信號的平穩段的最大幅值先增大后減小。這是因為當缺陷軸向長度增大時，缺陷反射的信號幅值增大；隨著缺陷軸向長度繼續增大，缺陷周圍界面反射波的相位差逐漸增大，當相位差超過半個漢寧窗的信號周期時，信號幅值符號相反，相互抵消，所以信號幅值下降。此外，不同長度的缺陷反射信號平穩段最大幅值相同時，可通過波形進行區分(見圖16)。

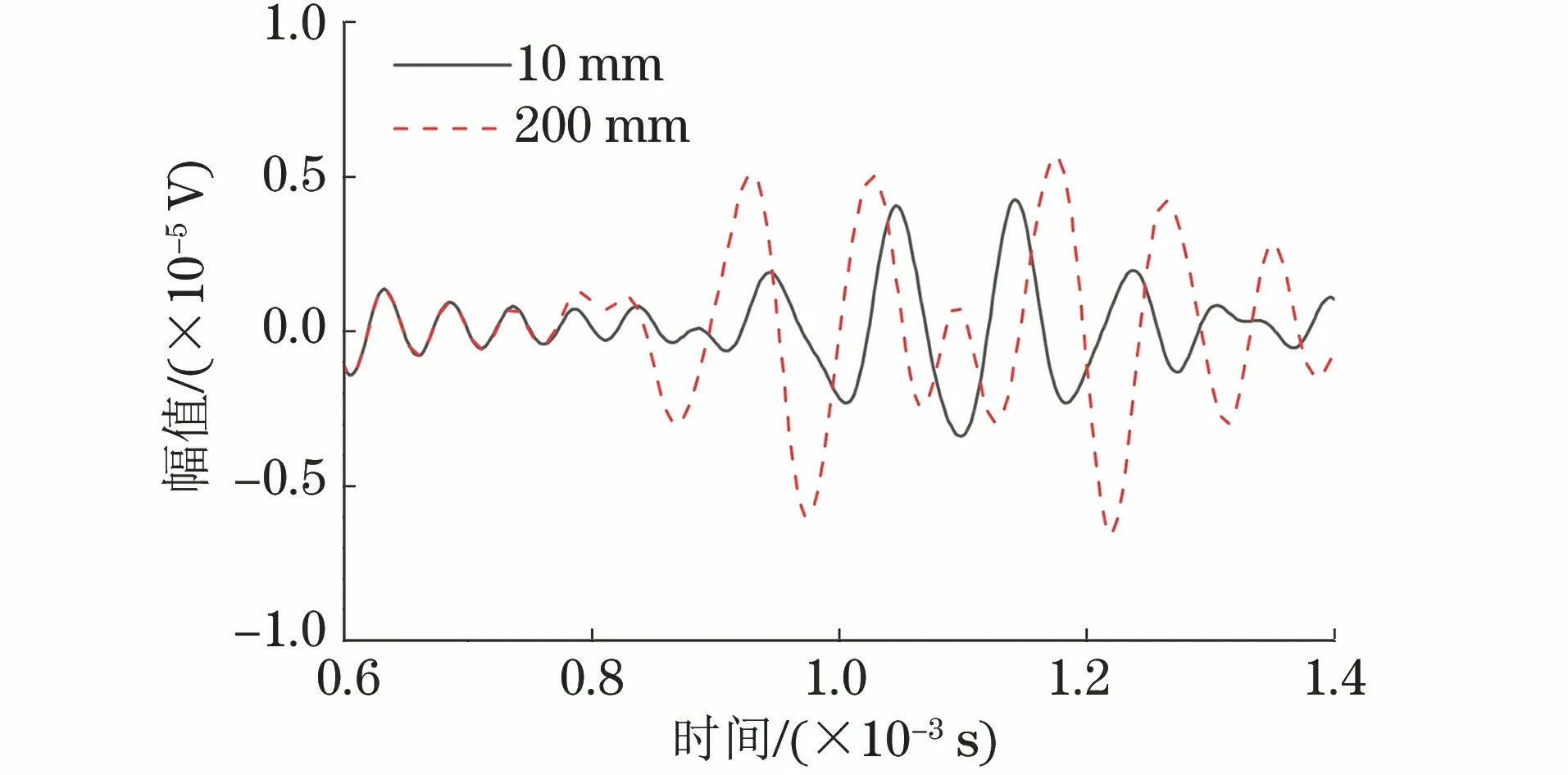
圖16 反射信號幅值相同但長度不同的缺陷波形

缺陷長度為10 mm的波形中間高兩邊低，而缺陷長度為200 mm的波形中間低兩邊高，這是信號疊加導致的，因此可以對兩信號平穩段最大幅值相同而缺陷長度不同的情況進行區分。

3 結語

(1) 激勵頻率不變而骨料面積占比增大時，首波波峰出現時間并不隨之發生變化，但幅值會逐漸減小；底端回波波峰出現時間呈線性提前，幅值也會逐漸減小。激勵頻率發生變化時，首波波峰和底端回波波峰的幅值隨著激勵頻率的升高而降低，導波傳播的速度隨之減慢。在頻散特性不明顯的激勵頻段內，檢測混凝土構件的導波回波信號中無缺陷情況下的信號平穩段幅值遠小于激勵信號段幅值和底端回波信號段幅值，可忽略不計。因此，缺陷檢測的關鍵就是確定頻散特性不明顯的激勵頻段。

(2) 當缺陷截面尺寸一定時，隨著缺陷軸向長度的增大，缺陷響應信號平穩段的最大幅值先增加后減小。