17-4PH不銹鋼熱老化的磁多參數無損評估
褚英杰,孫 琦,李乾武,史芳杰,黃 飛,楊廣宇
(1.福建寧德核電有限公司,寧德 352000;2.蘇州熱工研究院有限公司,蘇州 215000)
17-4PH(05Cr17Ni4Cu4Nb)馬氏體不銹鋼因具有較高的強度和優異的耐腐蝕性能,被廣泛應用于核電廠的高強度結構部件。17-4PH不銹鋼在高溫服役時會產生Cu顆粒析出、調幅分解、二次碳化物析出等現象[1],導致材料的沖擊功下降,硬度上升,脆性增加[2],增加了材料的脆性斷裂風險。因此,對17-4PH不銹鋼的熱老化評估具有重大意義。
不銹鋼或者合金鋼在熱老化過程中,因微觀組織的變化,其磁性能也會有相應的變化。BHATTACHARYA等[3-4]研究了磁巴克豪森噪聲(MBN)與17-4PH不銹鋼微觀結構的關系。其將17-4PH不銹鋼進行短時效熱老化以后,發現Cu沉淀增多,且Cu的沉淀可有效降低巴克豪森噪聲的峰值。GUPTA等[5]研究了不同時效階段下蠕變對12CrMoWV高溫合金鋼的增量磁導率的影響,結果表明,在550 ℃與650 ℃的不同時效下,增量磁導率曲線呈現相反的變化規律。
由于17-4PH不銹鋼熱老化過程中微觀組織變化的復雜,磁性無損檢測在17-4PH不銹鋼熱老化評估的工程應用上具有一定的難度。筆者在研究馬氏體不銹鋼熱老化后磁性變化規律的基礎上,比較了不同磁參數無損檢測方法的評估效果,引入人工神經網絡,為沉淀硬化馬氏體不銹鋼熱老化無損評估提供更可靠精確的方法。
1 試驗方法
試驗對象為某電廠的主蒸汽隔離閥閥桿,其材料為17-4PH不銹鋼,其材料成分如表1所示。

表1 17-4PH不銹鋼材料成分 %
為了模擬不同服役時間17-4PH不銹鋼熱老化的變化,同時縮短試驗周期,在350 ℃下進行加速熱老化試驗,具體加熱時間為0,100,300,500,1 000,2 000,3 000 h,共計7組樣品。對加速熱老化后的樣品進行力學試驗和磁參數測量。其中,沖擊試驗按照標準GB/T 229-2007的金屬材料夏比擺錘沖擊試驗方法要求,在JB-W450E-L型試驗機上進行試驗;按照GB/T 231.1-2009的金屬材料布氏硬度試驗方法測試材料的布氏硬度;采用LakeShore公司的VSM(振動樣品磁強計)平臺測試磁滯回線,樣品尺寸(長×寬×高)為1 mm×1 mm×3 mm;使用3 MA(多參數微磁顯微組織應力分析儀)進行磁多參數測試,各磁參數如表2所示。

表2 3MA測得的磁參數
2 試驗結果
2.1 力學試驗結果
對加速熱老化后的試驗樣品進行沖擊試驗與硬度測試,得到樣品沖擊功和硬度的變化趨勢如圖1所示。結果表明,17-4PH不銹鋼在熱老化后,沖擊功呈下降趨勢,而硬度呈上升趨勢。大量研究表明調幅分解是導致17-4PH不銹鋼脆性增加最主要的原因[6]。
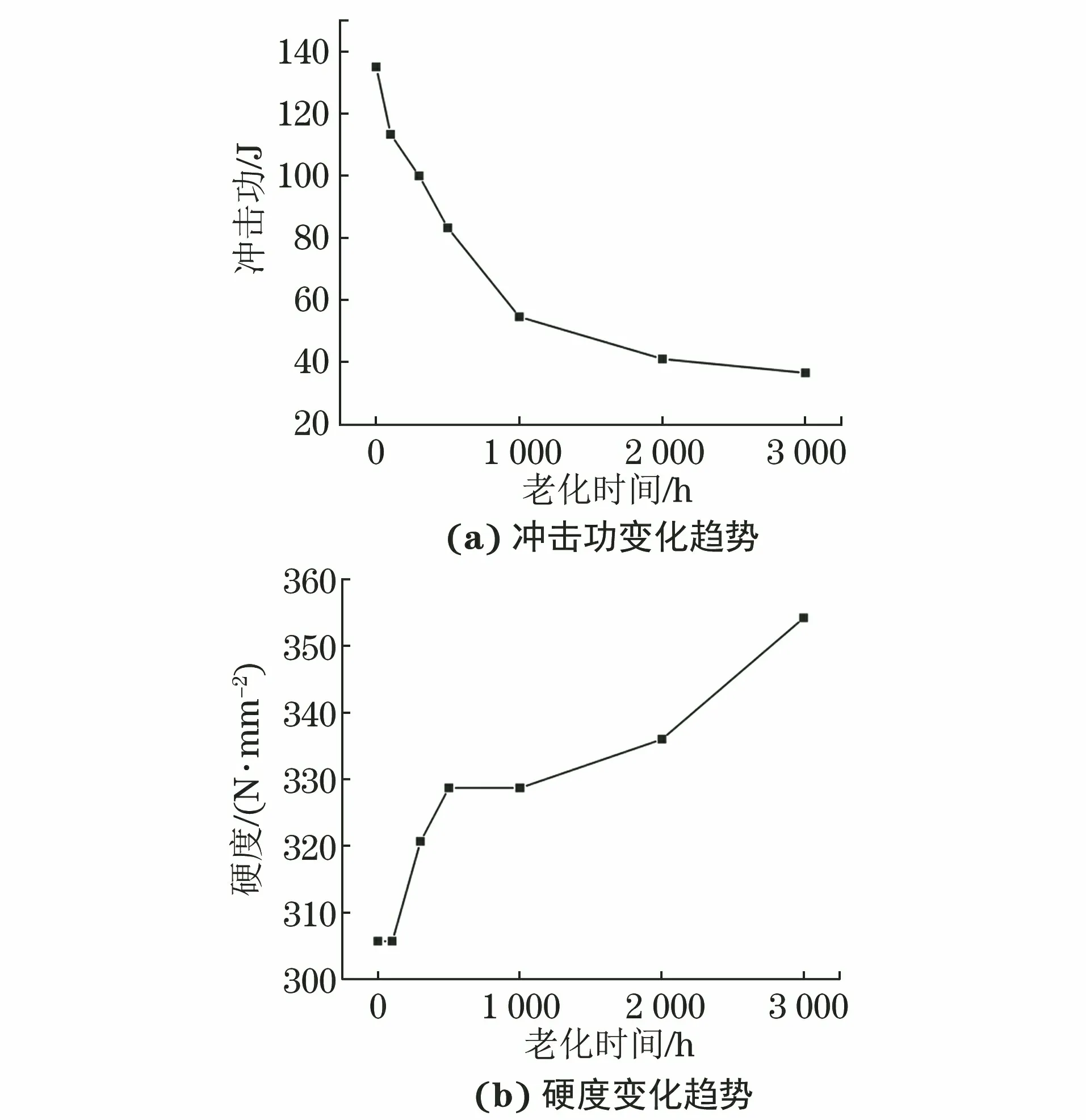
圖1 17-4PH不銹鋼熱老化后沖擊功與硬度的變化趨勢
2.2 磁參數測量結果
2.2.1 單一參數測量結果
通過VSM測得不同樣品的磁滯回線如圖2所示(1 T=104G, 1 emu=10-3A·m2)。由于17-4PH不銹鋼是軟磁材料,所以磁滯回線細長,磁滯損耗較小,即使在熱老化3 000 h后,17-4PH不銹鋼仍具有較低的矯頑力與磁滯損耗。這是因為材料在350 ℃下進行加速熱老化,該溫度遠低于純鐵的居里溫度[7]與常見鐵碳化合物的平均居里溫度[8],所以材料的磁性不會發生明顯的變化。17-4PH不銹鋼樣品的矯頑力與磁滯損耗隨熱老化時間的變化趨勢如圖3所示。
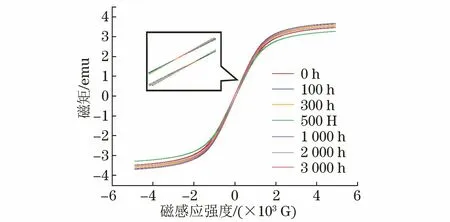
圖2 不同熱老化樣品的磁滯回線

圖3 不銹鋼樣品的矯頑力與磁滯損耗隨熱老化時間的變化趨勢
由圖3可知,材料的矯頑力最大波動范圍不超過3 A·m-1,而磁滯損耗的最大波動幅度不超過0.000 7 J,同時呈現無規律變化趨勢。3MA也對樣品的矯頑力進行了測試,得到矯頑力隨熱老化時間的變化趨勢(見圖4)。由圖4可知,矯玩力也呈無規律波動。

圖4 矯頑力隨熱老化時間的變化趨勢(3MA測試結果)
2.2.2 磁多參數測試結果
單一磁參數測試結果表明,17-4PH不銹鋼在熱老化過程中的矯頑力變化不大,而且呈現出無規律性的變化趨勢,無法有效表征17-4PH不銹鋼在熱老化過程中力學性能的變化規律。基于磁多參數,通過建立人工神經網絡模型,可以得到磁多參數與17-4PH不銹鋼的硬度、沖擊功之間的評估模型,并將模型評估的材料力學性能與試驗實測的力學性能進行對比。
試驗選取結構簡單的雙層前向型神經網絡模型,輸出層為線性神經元,輸入測得的25個磁參數,選擇隱藏層的激勵函數為tansig函數(將磁參數作為n,代入函數),其表達式為
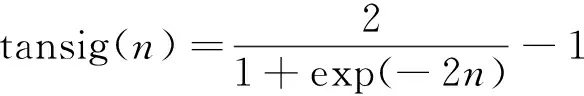
(1)
選取合適的隱藏層節點數,以L-M算法訓練神經網絡。沖擊功與硬度的模型評估結果和試驗結果的關系曲線如圖5所示。
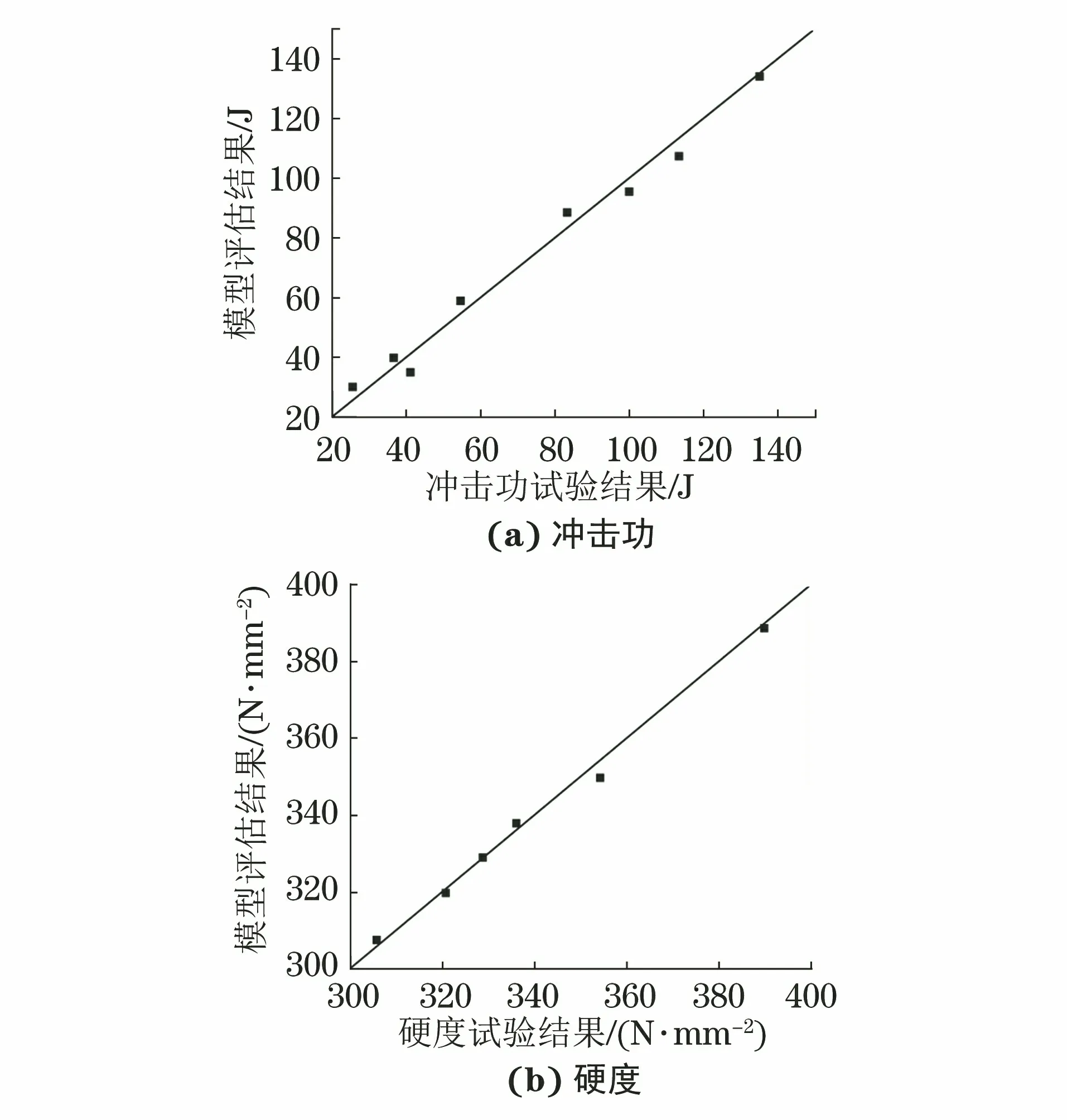
圖5 沖擊功與硬度的模型評估結果和試驗結果的關系曲線
經過訓練,可得到一個神經網絡模型,將待評估材料的25個磁性參量作為輸入,輸出結果為材料的力學性能評估結果。
結合圖3與圖5可知,即使在單一參數無規律的情況下,也可通過大量的磁多參數檢測數據,應用人工神經網絡,建立起精度較高的評估模型。
3 分析與討論
3.1 隱藏層節點數量對模型的影響分析
隱藏層節點數對模型的影響有:① 節點數會影響模型的運算速度,節點數越多計算時間就越長;② 節點數越多,擬合效果越好,超過一定數目,會出現過擬合現象。因此,需要選取合適的節點數目以保證良好的擬合效果。
圖6為節點數分別為10,30,50,70時擬合誤差柱狀圖(強度表示誤差在每個區間分布的統計相對數量,無量綱),在10節點和30節點時,誤差分布呈正態分布。對于10節點模型,較多誤差均分布在0誤差線兩側;在擬合節點超過30以后,誤差多數分布在0誤差線左右;50節點與70節點模型的誤差分布類似,此時再增加節點數的效果已經不明顯了。為了進一步研究節點數增加對擬合效果的影響,可分析擬合度隨隱藏層節點數增加的變化趨勢(見圖7)。
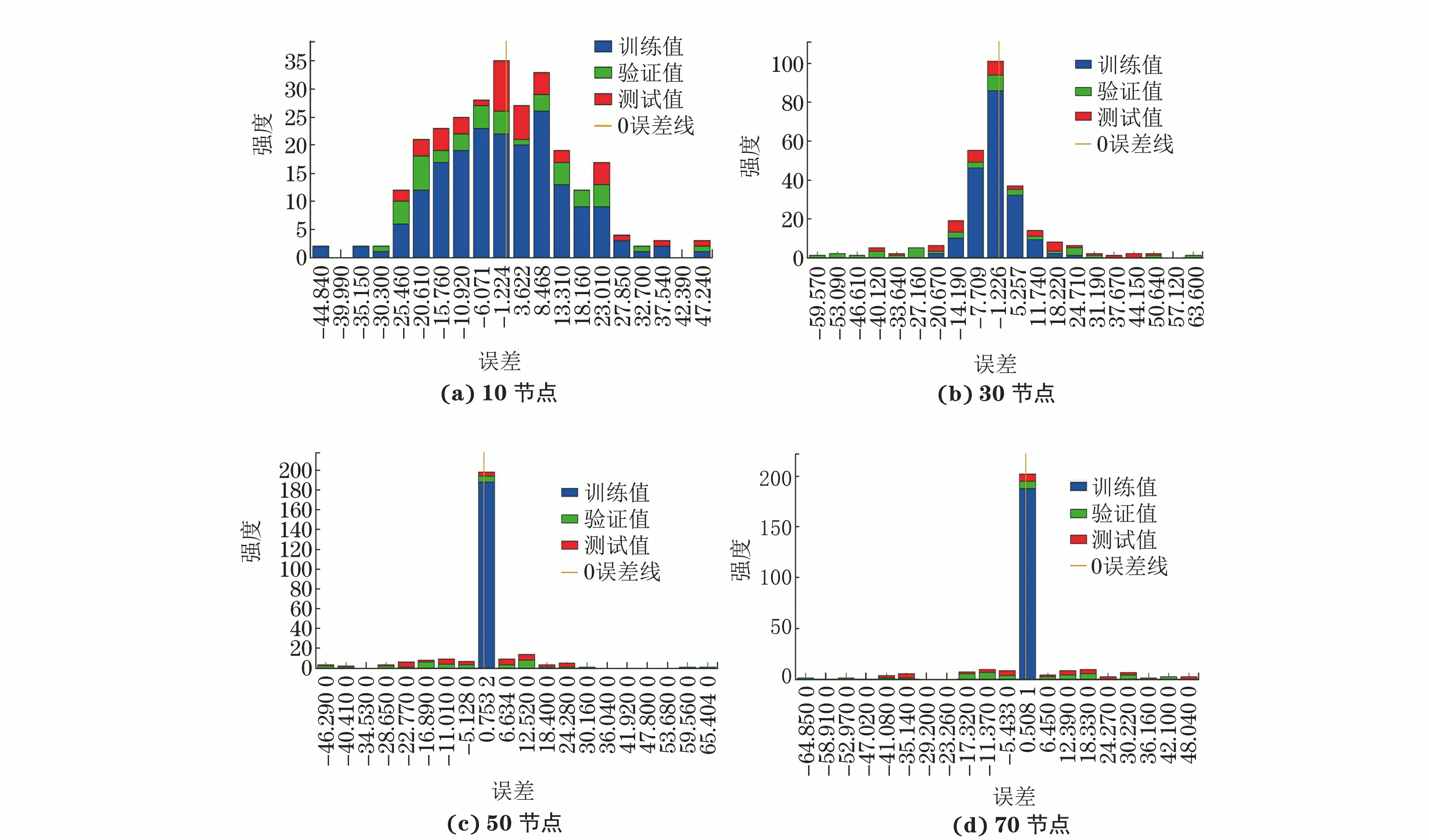
圖6 不同隱藏層節點數的誤差柱狀圖

圖7 擬合度隨隱藏層節點數的變化趨勢
一般來說,選取節點數可根據輸入層的節點數大致確定,而多數情況下需要研究節點數與擬合效果之間的關系來得到最優化的神經網絡模型。由圖7可知,節點數越多,訓練值的擬合效果越好,但是對新出現的樣本的適應性卻下降,無法較好地擬合,也就是說隱藏層節點數在超過一定限值后,神經網絡的擬合效果反而會下降。
3.2 訓練算法對模型的影響分析
常用的訓練算法有:L-M算法;貝葉斯正則化算法;量化共軛梯度算法。L-M算法使用一種廣泛的非線性最小二乘算法,通過對待測參數作線性近似,將問題轉化為最小二乘問題,因而計算量相對較少,可很快地達到收斂狀態;貝葉斯正則化在基于L-M算法的基礎上,更新優化權重和偏置,生成普適性更強的神經網絡;量化共軛梯度算法基于共軛方向,具有收斂快,占用內存小等特點。筆者分別從算法運算速度,擬合效果兩方面綜合比較3種模型。
選擇隱藏層節點數為40,分別以3種算法建立神經網絡模型,比較3種算法的特性,對比結果如表3所示。
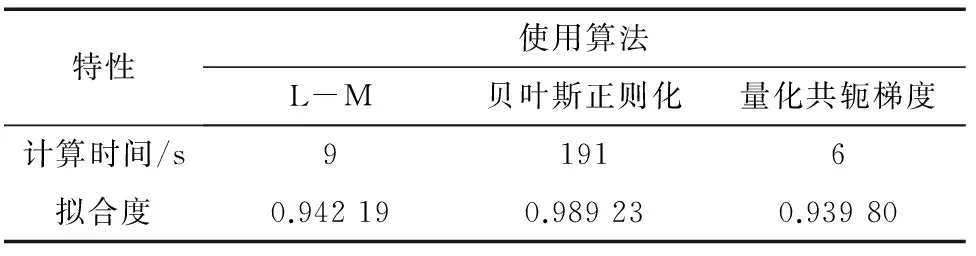
表3 3種算法的對比
綜合分析來看,L-M算法計算所需時間較短,且模型的擬合度較高,因此L-M算法在實際應用中更為實用。貝葉斯正則化迭代次數需要到1 000次時結果才收斂,而L-M算法和量化共軛梯度算法分別在60次和7次迭代后收斂,在一定程度上保證了結果不會過擬合。
基于磁多參數,可以利用人工神經網絡,可以給出磁性參數與力學性能之間的描述模型,且評估速度快。
4 結論
(1) 17-4PH不銹鋼在熱老化后,沖擊功下降,硬度上升,說明熱老化導致其脆性增加。
(2) 單一的磁參數測量結果表明,17-4PH不銹鋼在350℃下熱老化后,其矯頑力、磁滯損耗均在小范圍內波動,且呈無規律變化,說明單一的磁參數測量方法不適用于評估17-4PH不銹鋼的熱老化。
(3) 基于磁多參數,應用人工神經網絡,可建立評估17-4PH不銹鋼熱老化的模型,其評估效果較好,可以解決單一磁參數無法評估17-4PH不銹鋼熱老化的問題。在應用人工神經網絡建立17-4PH不銹鋼評估模型時,需要選取合適的網絡節點數及合適的算法,可有效提升建模效率,得到較好的精度。

