p(Vm ? b) = RT實際氣體在一些熱力學過程中的應用

金明善，楊樹斌，李慶忠

煙臺大學化學化工學院，山東 煙臺 264005

理想氣體在各個熱力學過程中的應用是物理化學的重要基礎知識，要求學生熟練掌握，但是理想氣體作為一個常用系統，過于簡單，學生學習后很容易形成誤解，例如經常把等溫過程熱力學能不變的這種特殊性質當成一般性質濫用于其他氣體，因此，在教學中先讓學生牢固掌握理想氣體的基本性質及其應用的基礎上，了解實際氣體在一些熱力學過程中的應用是非常必要的。由于van der Waals方程的數學處理又過于復雜，因此作為過渡，介紹p(Vm? b) = RT實際氣體的一般性質及其在部分熱力學過程中的應用有很好的教學示范作用。

1 p(Vm ? b) = RT實際氣體的一般性質及其在兩種常見熱力學過程中的應用

1.1 熱力學能

熱力學能的熱力學基本方程為dU = TdS ? pdV，在等溫條件下，等式兩邊對體積求導得，

將麥克斯韋關系式(?S/?V)T= (?p/?T)V代入，得

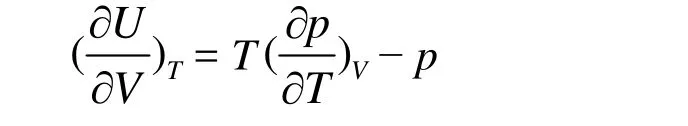
因為 p = RT/(Vm? b)，所以(?p/?T)V= R/(Vm? b)，代入得(?U/?V)V= RT/(Vm? b) ? p = 0，即

這說明p(Vm? b) = RT，實際氣體的熱力學能僅僅是溫度的函數，即該氣體在等溫過程中熱力學能保持不變，ΔU = 0，該結果可以表達為以下三種形式：

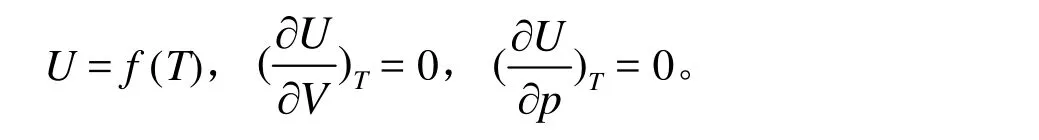
設 U = f (T，V)，則其全微分關系式為 dU = CVdT + (?U/?V)TdV，因為(?U/?V)T= 0，得到

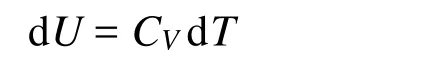
這個求熱力學能的公式適用于該氣體的任何過程，也就是該氣體在非等溫過程：絕熱、等壓、等容、任意過程中，熱力學能的變化均可以用dU = CVdT求得，這一點相同于理想氣體。

1.2 等壓熱容與等容熱容之間的關系

p(Vm? b) = RT 可以表達為 pV = nRT + nbp，V = nRT/p + nb，(?V/?T)p= nR/p，(?U/?V)T= 0 代入上式，得Cp? CV= nR 或 Cp,m? CV,m= R

理想氣體等壓熱容與等容熱容之間的關系也具有上述表達式。

1.3 在等溫過程中各種熱力學量的計算

當p(Vm? b) = RT實際氣體由始態(p1，V1)，經過等溫過程到達終態(p2，V2)，因為該氣體的熱力學能僅僅是溫度的函數，所以等溫過程中ΔU = 0，Q = ?W，因為熱和體積功是過程量，所以在等溫過程的三個不同途徑，即絕熱向真空膨脹、等溫等外壓、等溫可逆過程的求法分別不同，而H、S、A、G是狀態函數，ΔH、ΔS、ΔG、ΔA在上述始終態相同的三個不同途徑，具有相同的值。具體計算如下表1所示。

表1 p(Vm ? b) = RT實際氣體在等溫不同途徑各種熱力學量的計算

通過表中的總結可以看出，W、Q、ΔU、ΔS、ΔA用壓力表示的表達式與理性氣體相同，而ΔH和與焓相關的ΔG的表達式與理性氣體不同。

[例1] (中國海洋大學2005年碩士研究生入學試題)某實際氣體狀態方程為pVm= RT + bp，式中b為大于0的常數，當該氣體經絕熱向自由膨脹后，氣體的溫度__________。

[解] 該氣體經絕熱向自由膨脹過程，Q = 0，W = 0，ΔU = 0，因為該氣體的熱力學能僅僅是溫度的函數，所以溫度不變。

[例2] (南京大學2004年碩士研究生入學試題)一直到1000p?，氮氣仍服從下列狀態方程式p(Vm?b) = RT，式中常數 b = 3.90 × 10?2dm3?mol?1，在 500 K，1 mol N2(g)從 1000p?等溫膨脹到 p?，計算ΔU、ΔH、ΔS、ΔG、ΔA。

[解] 前已證明p(Vm?b) =RT實際氣體的熱力學能僅僅溫度的函數，在該等溫過程中：ΔU= 0

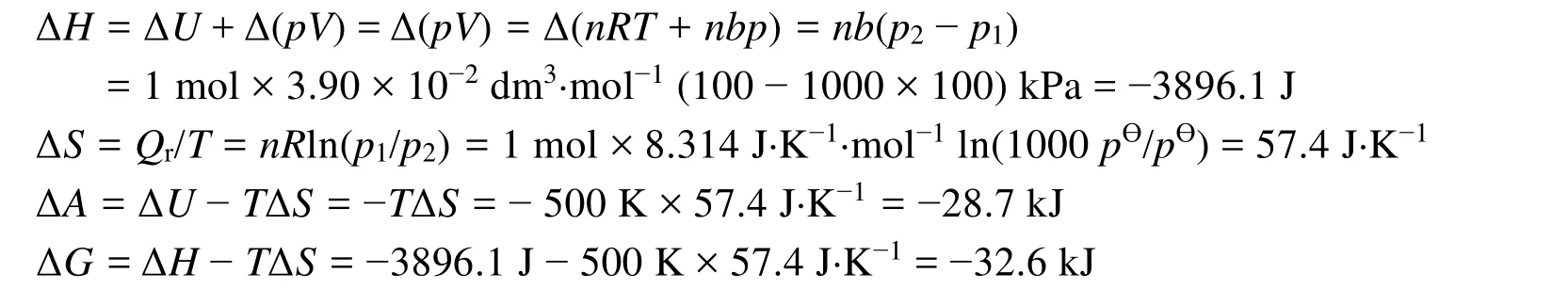
1.4 絕熱可逆過程

絕熱可逆過程Qr= 0，所以δW =dU，因為該氣體任何過程dU = CVdT，所以

p(Vm? b) = RT，其中b是大于零的常數。

(1) 證明該氣體的熱力學能只是溫度的函數；

(2) 推出該氣體的絕熱可逆過程方程：T2/T1= [(V1? nb)/(V2? nb)]R/CV,m

[解]

(1) 證明該氣體的熱力學能只是溫度的函數，請參考前面的內容；

(2) 該氣體的絕熱可逆過程方程的推導，請參考前面的內容，其中溫度和體積之間的關系為：

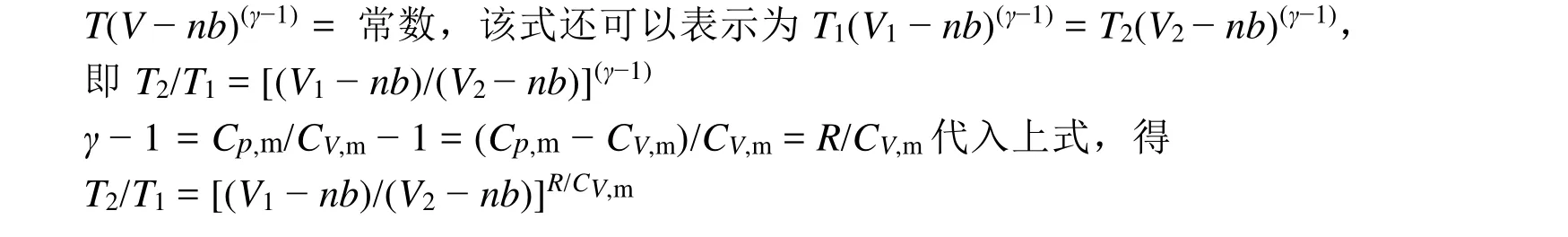
2 p(Vm ? b) = RT實際氣體在兩個實驗過程中的特點

2.1 Joule實驗

焦耳實驗中氣體發生絕熱向真空膨脹過程，因為Q = 0，W = 0，所以ΔU = 0，溫度保持不變，所以

2.2 Joule-Thomson實驗

等焓、絕熱、壓力減小是Joule-Thomson實驗的三大基本特征，可以用Joule-Thomson系數μJ-T=(?T/?p)H衡量氣體節流膨脹后制冷或制熱的能力[4]。

因為在節流膨脹過程中壓力減小p2< p1，所以T2> T1，即該氣體節流膨脹后溫度升高，這說明p(Vm?b) = RT實際氣體無法通過節流膨脹進行液化。

[例4] (中國科學院大學2000年碩士研究生入學試題)已知1 mol氫氣的物態方程

p(V ? b) = RT，(b > 0)，若該氣體經一個絕熱的自由膨脹過程由始態(T1，V1)到達終態體積V2。求：(1) 終態的溫度T2；

(2) 過程的 ΔU、ΔH、ΔS；

(3) 計算說明該氣體經過節流膨脹后，溫度如何變化？

[解]

當物質的量為1 mol時，p(Vm? b) = RT實際氣體物態方程為p(V ? b) = RT，前面已證明該氣體的熱力學能僅僅是溫度的函數和Joule-Thomson系數μJ-T= ? nb/Cp< 0。

(1) 因為在絕熱自由膨脹過程中Q = 0，W = 0，所以ΔU = 0，所以溫度保持不變，T2= T1，即該氣體絕熱自由膨脹過程為等溫過程。

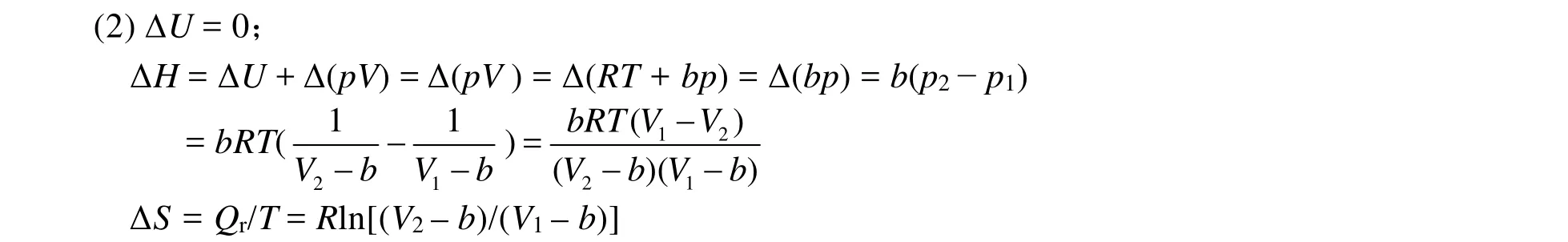
(3) μJ-T= (?T/?p)H= ?(1/Cp)(?H/?p)T= ?b/Cp< 0，因為節流膨脹過程 p2< p1，所以 T2> T1，說明該氣體經過節流膨脹后，溫度升高。

3 p(Vm ? b) = RT實際氣體的化學勢及其應用

3.1 化學勢等溫式

根據物態方程pVm= RT + bp，Vm= RT/p + b，代入dμ = Vmdp中

美國化學家G. N. Lewis提出了逸度f的概念，對壓力進行了修正之后，p(Vm? b) = RT實際氣體的化學勢表達式為

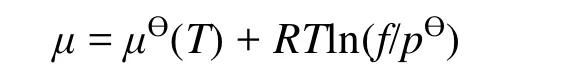
其中逸度 f=γp，γ為逸度系數。

3.2 逸度系數的求法

3.3 五個熱力學函數

通過化學勢的表達式 μ(T, p) = μ(T, p?) + RTln(p/p?) + b(p ? p?)，可以分別推導五個熱力學函數的表達式：

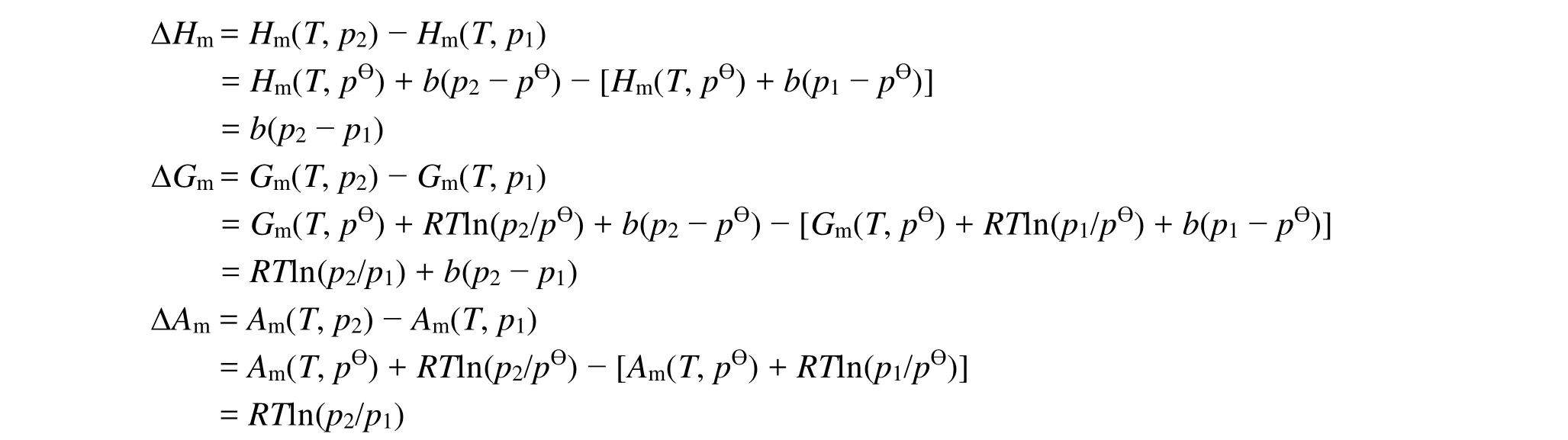
利用化學勢導出的五個熱力學函數的表達式來推導p(Vm? b) = RT實際氣體在等溫過程中五個熱力學函數的變化，得出了與前面一致的結果。

[例5] 設氣體B遵守下列物態方程pVm= RT + bp (b為大于零的常數)。

(1) 請導出其化學勢、熵、焓的表達式；

(2) 導出在(T, p1) → (T, p2)過程的逸度比；

(3) 設B在p?為理想氣體，求其在298 K，20p?的逸度[3]。

由以上內容可以總結，p(Vm? b) = RT實際氣體的熱力學能僅僅是溫度的函數、等壓熱容與等容熱容之差Cp? CV= nR，等溫、絕熱可逆等熱力學過程中，用壓力表示的一些熱力學量的計算與理想氣體具有相同的性質，通過做大量的習題可以更深入地掌握該氣體和理想氣體之間的聯系和區別，進一步探索其他更復雜的實際氣體的熱力學性質。