基于LSTM網絡的浮式海洋平臺運動在線預報研究

李昊波，肖龍飛,2，魏漢迪,2，劉明月,2

（1.上海交通大學海洋工程國家重點實驗室，上海200240;2.高新船舶與深海開發裝備協同創新中心，上海200240）

0 引 言

隨著海洋開發規模與領域的不斷擴大，船舶和海上平臺等浮式結構物的重要性日益凸顯。與固定或陸地上的結構物不同，海上浮式結構物始終處于多自由度搖晃中，使其海上作業和安全都受到嚴峻的挑戰。因此，對海上浮式結構物的運動進行準確可靠的在線預報，在指導作業、保障安全等方面具有重要意義。

運動在線預報一般基于運動歷史數據采用時間序列分析方法、非線性系統理論、機器學習技術等手段預報未來幾秒到幾分鐘的海上浮式結構物的運動響應[1]，可分為極短期運動預報和安穩期預報。對浮式結構物的極短期運動響應預報在固定翼艦載機回收、提高艦載武器發射精度、改善動力定位控制性能等方面均具有重要意義。

極短期預報提前量一般為幾秒，相對較短，但對預報精度要求較高。按照采用的數學方法分類，可以把極短期預報分為兩類：其一是以傳統的物理和數學方法如微積分和統計學等為基礎的預報模型，有時間序列模型、卡爾曼濾波模型等；其二是以神經網絡、模糊數學等現代方法為手段的模型，如神經網絡模型、小波分析預報模型等[2]。Triantafyllou 等[3-4]利用Kalman 濾波技術為基礎的方法對船舶的6 個自由度運動進行預報，發現有義波高、艏搖和噪聲等因素對預報精度影響很大，在無噪聲情況下橫搖可預報到10 s，在有噪聲情況下可預報提前量僅為2～3 s，且預報誤差沒有給出[4]。Khan 等[5]采用人工神經網絡技術對橫搖運動進行了預報，預報提前量為6 s 時可信度為60%，預報提前量為10 s時可信度僅為40%。Huang等[6]基于AR-EMD 方法對船舶縱搖和垂蕩運動進行了極短期預報，在預報提前量為10 s 時，精度分別為85%和84%。Peng 和Liu[7]基于格型遞歸最小二乘法對船舶橫搖運動進行了預報，在預報提前量為15 s時，精度為81%。楊震等[8]基于經驗模式分解，利用支持向量機對船舶橫搖運動進行預報，預報提前量為10 s時的誤差為0.09。目前關于船舶的運動預報較多，而關于浮式海洋平臺的運動預報較少，尤其是縱蕩、橫蕩運動。總體上，在線預報目前表現一般，模型計算復雜度高，誤差隨預報提前量增加而非線性增長，難以實用。本文根據近年來廣泛應用的長短期記憶（LSTM）神經網絡技術提出一種新的運動預報模型，應用于浮式海洋平臺運動響應的極短期預報，在保證計算效率的情況下，可以得到準確的運動預報結果。

1 LSTM 模型

1.1 循環神經網絡和LSTM

浮式海洋平臺在實際不規則波環境中的六自由度運動響應具有很強的隨機性、非線性以及時間依賴性，傳統的數學、力學方法求解復雜費時，很難應用于需要實時獲得響應數據的運動在線預報。神經網絡技術則十分適合用于此類問題，即模擬一組數據到另外一組數據的映射。本研究的思路為：把不規則波浪時歷到運動響應的映射看成是一種復雜的、未知的映射函數，使用神經網絡來擬合此函數，最終得到輸入為波浪時歷，輸出為運動響應的神經網絡模型。

針對浮式海洋平臺運動響應的預報，傳統的神經網絡模型尚難以實現。這是因為海洋平臺在t時刻的運動響應不僅取決于該時刻的波浪作用，還取決于t-1時刻海洋平臺的狀態；而t-1時刻海洋平臺的狀態同樣不僅取決于t-1 時刻的波浪作用，還會受到t-2 時刻海洋平臺狀態的影響，依次類推。因此，浮式海洋平臺的運動響應具有時間依賴性，若要準確預報海洋平臺的運動響應就需要把隨時間傳遞的信息應用到預報模型當中。循環神經網絡（RNN）恰好可解決這一問題，在處理時間序列相關的數據方面具有很好的效果。

RNN 的單元展開圖如圖1所示，x為網絡輸入，s為隱藏層，o為網絡輸出，U 為輸入到隱藏層權重，V為隱藏層到輸出權重，W 為隱藏層到隱藏層權重。與傳統神經網絡不同，在RNN 中每一層網絡共享權重，這樣會有效地減少網絡中需要訓練的參數，縮短了訓練時間。但RNN 存在梯度消亡問題，來自之前的記憶信息對輸出的影響會逐漸衰減趨于消失或者呈指數爆炸增長，從而嚴重影響模型的收斂速度與性能。

LSTM最早由Hochreiter和Schmidhuber[9]提出,并經由Grave[10]改進，有助于解決RNN的梯度消亡問題。LSTM 的單元結構[10]如圖2 所示，每個LSTM 單元中存在細胞（Cell）用于描述單元當前狀態，也存在3 個控制門，即輸入門（Input Gate），輸出門（Output Gate）和遺忘門（Forget Gate），分別用于控制輸入、輸出以及細胞的狀態。當控制門打開時，表示允許所有信息通過；控制門關閉時，表示不允許任何信息通過。其方程如下：

式中，ft為遺忘門方程；ct為輸入門方程，用以更新細胞狀態；ot為輸出門方程，與ct共同輸出ht。

圖1 循環神經網絡單元展開圖[11]Fig.1 An unfolded CNN network

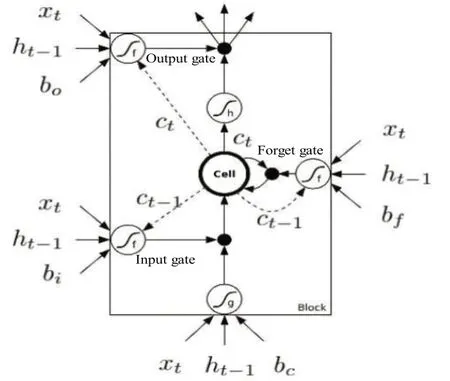
圖2 LSTM單元結構[10]Fig.2 LSTM memory block with one cell

LSTM 可歸納為圖3 所示的幾種類型，針對由波浪序列預報海洋平臺運動問題，本文采用多對一類型，使用一串波浪序列預報一個運動響應值。圖4解釋了利用波浪序列預報運動響應的思路，顯示了預報提前量為5 s的模型輸入輸出映射關系，t時刻的運動響應由t-15到t-5時間段的波浪序列預報得出。

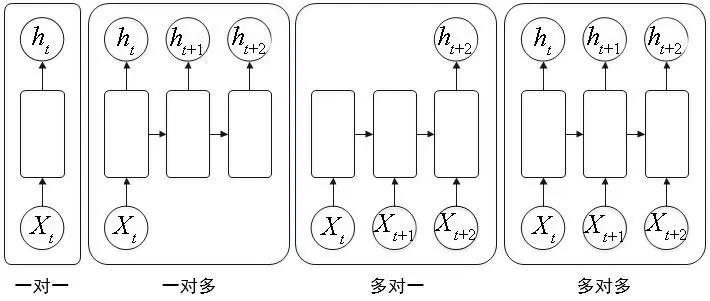
圖3 LSTM類型Fig.3 Types of LSTM

1.2 LSTM模型結構

本文所構建的LSTM 模型具有一層LSTM 隱藏層和一層輸出層，如圖5 所示。考慮到波浪和平臺運動的周期，設置LSTM 模型的時間步長為128 個時間序列點，以及考慮波浪和運動之間映射的復雜度，設置LSTM 模型隱藏層節點數為256。此兩項參數作為超參數，根據經驗和實際嘗試確定。

輸入層：輸入數據是長度為128 的向量，其物理意義是長度為128的波浪序列，代表此模型的時間步長被設置為128，輸入特征維度為1。

隱藏層（LSTM）：隱藏層有256 個節點，其接受形狀為（None，128，1）的輸入，輸出形狀為（None，256）的向量。

輸出層（Dense）：是一個全連接層，其輸入數據為隱藏層（LSTM）輸出的形狀為（None，256）的數據，輸出為運動響應值。

本文采用隨迭代次數降低學習率的技巧來幫助神經網絡模型的訓練。學習率是調整神經網絡的重要超參數之一，如果學習率過高，則會導致不收斂或者振蕩現象產生。但是如果學習率過小，訓練時間會較長，且會容易陷入局部最優。因此，令學習率隨迭代次數降低是一種有效的解決方法。一旦驗證集誤差不再降低，學習率就會被設置為原先的十分之一。

另外，使用Dropout技巧防止過擬合[12]。Dropout主要將隱藏層中的神經元在每一次訓練過程中按照一定概率進行丟棄，此部分權重在本次訓練過程不進行更新，從而實現了“取平均”和減少神經元之間復雜的共適應關系的作用，可有效地防止過擬合的產生。

圖5 LSTM網絡模型結構Fig.5 LSTM model structure

2 海洋平臺模型試驗數據

本文訓練數據來自于一座半潛式鉆井平臺的運動響應試驗，試驗在上海交通大學海洋工程國家重點實驗室深水試驗池進行。水池的幾何尺度及平臺模型布置如圖6 所示，采用4 點水平系泊系統，系泊纜由細鋼絲繩與軟彈簧構成，與平臺坐標軸成45°對稱布置。考慮180°浪向，試驗水深為10 m。所研究的半潛式鉆井平臺為典型的四立柱、雙浮箱、箱型甲板型式，主要參數見表1，外形輪廓如圖6所示。模型縮尺比λ為56。

圖6 深水池布置及半潛式平臺模型Fig.6 Deepwater offshore basin layout and the semi-submersible model

開展的不規則波試驗共有40個工況，考慮4種海況，如表2所示。其中不規則波W1與W2各4個隨機時間序列，W3 與W4 各16 個隨機時間序列。試驗采樣頻率為100 Hz，每個工況測量得到的試驗數據超過160 000 點，保證了訓練數據的充分性。采用所建立的LSTM 神經網絡模型，使用其中34 個不規則波試驗工況數據（W1 與W2 各3 個，W3 與W4 各14 個）對LSTM 模型進行訓練，剩下的6 個工況數據用于測試神經網絡模型預報運動響應的性能。

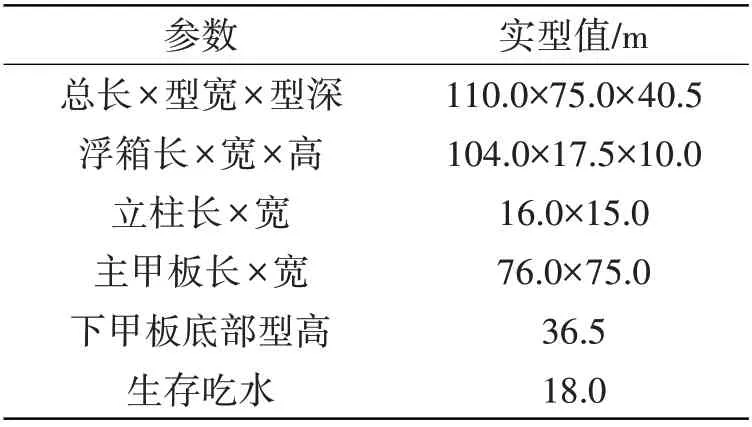
表1 半潛式平臺參數Tab.1 Main particularities of the semi-submersible

表2 波浪環境參數（JONSWAP）Tab.2 Environment matrix（JONSWAP）

3 預報結果與分析

使用經過34個工況試驗數據進行訓練后得到的LSTM 模型，對迎浪狀態（180°）6個測試工況下半潛式平臺的縱蕩、垂蕩以及縱搖運動進行預報，預報提前量分別設置為0 s、6 s 和12 s。LSTM 模型的運動時歷預報結果如圖7～9所示，其中虛線代表試驗的實測值，實線代表預報值。由于時間序列長度過于巨大，所以從時間序列起始、中間和末尾三個時間段各選取了300 s時間長度進行結果對比。

圖7 不同預報提前量下的縱蕩運動預報與測量結果對比Fig.7 Comparison between predicted and measured surge motions for different forecast durations

圖8 不同預報提前量下的垂蕩運動預報與測量結果對比Fig.8 Comparison between predicted and measured heave motions for different forecast durations

圖9 不同預報提前量下的縱搖運動預報與測量結果對比Fig.9 Comparison between predicted and measured pitch motions for different forecast durations

從圖7～9 可以看出，在各個預報提前量情況下，LSTM 模型對平臺運動響應的預報結果均較為準確，預報值很好地擬合了實測值。不設置提前量的情況下，預報結果精度較高，在可以提前測量波浪的情況下，此模型具有很大的應用價值。在預報提前量為6 s的情況下，預報精度稍有降低，所以此模型可以實現對海上浮式結構物較高精度的極短期預報。而在預報提前量為12 s 的情況下，預報精度有所降低，但預報時間得以延長，使得此模型適用性更為廣泛。同時可以看到，在預報提前量為12 s的垂蕩預報情況下，存在相位差，這是由于起始數據都接近0 且預報時間偏長的原因，但由于振幅小且位于運動啟動階段，對實際應用影響可不考慮。

根據運動響應預報曲線和實測曲線的相關系數，可計算得到LSTM 模型對于測試工況的預報精度，結果如表3 所示。可見，盡管預報精度隨預報提前量的增加而降低，然而在預報提前量為12 s時，縱蕩預報精度仍為90%，垂蕩預報精度可達93%，縱搖預報精度稍低，在85%以上。總體而言，運動預報結果具有較高精度，使用LSTM模型預報浮式海洋平臺運動具有較高的可行性。三種運動響應預報的精度結果對海況和訓練數據變化的敏感程度不同，從W1 至W4，波高逐漸增加，用作訓練數據的工況數也從3 個增加到14 個，基于LSTM 模型的垂蕩和縱搖預報精度也逐漸提高，而縱蕩的預報精度始終較高，對海況和訓練數據變化不敏感。

表3 不同測試工況下運動預報精度統計結果Tab.3 Prediction accuracy statistics under different test cases

運動響應的均方差表征了運動幅值的大小，表4 所示為不同測試工況下運動測量值與預報值的均方差結果對比。可見，三種運動響應預報結果的均方差均接近于測量值,縱蕩均方差相對誤差最小，縱搖結果的相對誤差較大。預報值的均方差相比于測量值都偏小，表明所構建的LSTM 模型在預報運動響應時偏于保守。

表4 不同測試工況下運動測量值與預報值均方差對比Tab.4 Comparison of standard deviations between measured and predicted motions under different test cases

續表4

此外，計算效率是在線預報實時性的基礎。使用神經網絡模型進行運動響應的預報，在考慮預報精度的同時，還必須考慮計算效率的影響，即每一步的計算時間都應該遠小于預報提前量。本文LSTM 模型的參數量為264 449，在個人電腦上平均每步計算時間約為10 ms，相對于預報提前量6 s和12 s而言極小，故模型計算效率可滿足實際應用的實時預報要求。

4 結 論

基于機器學習理論，本文建立了浮式海洋平臺運動預報的LSTM 神經網絡模型，通過采用半潛式平臺模型試驗大量運動響應數據的學習訓練，并對不同測試工況進行運動預報和分析，得到了不同預報提前量時的模型預報精度。結果表明：

（1）所建立的LSTM 模型應用于浮式海洋平臺運動極短期在線預報具有較高的可行性，預報提前量為12 s時，縱蕩、垂蕩和縱搖預報精度可分別達到90%、93%和85%以上。

（2）所構建LSTM 模型在預報縱蕩運動時的精度隨海況和訓練數據的變化不明顯，而在預報垂蕩和縱搖運動時的精度對海況和訓練數據變化敏感，隨波高和訓練數據的增加而精度提升，模型預報運動響應結果偏于保守。

（3）LSTM 模型每步計算時間為毫秒級，遠小于預報提前時間，實時性高，可以實現對浮式海洋平臺運動響應的在線預報。在實際中，應用LSTM模型可以對浮式海洋平臺的作業進行安全預報或主動進行提前控制，也可以拓展到船舶運動預報。